1.2.1 定义与命题 课件(共29张PPT)
文档属性
| 名称 | 1.2.1 定义与命题 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-10 15:19:56 | ||
图片预览






文档简介
(共29张PPT)
第一章 三角形的初步知识
1.2.1 定义与命题
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.了解定义的含义.了解命题的含义.
2.了解命题的结构,会把命题写成“如果……那么……”的形式.
3.通过本节学习,培养树立科学严谨的学习方法.
02
新知导入
小华与小刚正在津津有味地阅读《我们爱科学》.
这个黑客终于被逮住了.
是的,现在的因特网广泛运用于我们的生活中,给我们带来了方便,但…….
这个黑客是个小偷吧?
可能是个喜欢穿黑衣服的贼.
坐在旁边的两个人一边听着他们的谈话,一边也在悄悄地议论着.
03
新知探究
“鸟是动物.”
“鸟是动物吗 ”
这两个句子在叙述上有什么区别
03
新知探究
人们在交流时常需要应用许多名称和术语.为了不产生歧义,对这些名称和术语的含义必须有明确的规定.
如:(1)商店以比原来标价低的价格出售商品叫做 ;
打折
(2)单位体积内所含有某一物质的质量叫做 ;
(3)在同一平面内不相交的两条直线叫 .
密度
平行线
03
新知讲解
03
新知讲解
提炼概念
一般地,能清楚地规定某一名称或术语的意义的句子叫做该名称或术语的定义.
下列语句中,属于定义的是( )
A.对顶角相等.
B.三条边对应相等的两个三角形全等.
C.在同一平面内三条线段首尾顺次连接组成的
图形叫做三角形.
D. 同旁内角互补,两直线平行.
C
03
新知讲解
请说出下列名词的定义:
(1)无理数 (2)直角三角形
(3)角平分线 (4)平方根
(1)无限不循环小数是无理数.
(2)有一个角是直角的三角形是直角三角形.
(3)在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的平分线.
(4)一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
03
新知讲解
比较下列句子在表述形式上,哪些对事情作了判断?哪些没有对事情作出判断?
⑴对顶角相等; ⑵画一个角等于已知角;
⑶两直线平行,同位角相等; ⑷a、b两条直线平行吗?
⑸鸟是动物; ⑹若a2=4,求a的值;
⑺若a2= b2,则a=b; (8)三角形三个内角的和等于1800.
句子_____________ 对事情作了判断;
句子 没有对事情作出判断.
(1)
(3)
(5)
(7)
(2)
(4)
(6)
一般地,判断某一件事情的句子叫做命题.
(8)
命题
不是命题
03
新知讲解
“两只脚的动物是鸡”是不是一个命题呢?
定义是不是
命题呢?
温馨提示:
(1)疑问句和祈使句都不是命题
(2)只需考虑是否作了判断,不需要考虑判断的结果是否正确
03
新知讲解
下列语句中,__________________是命题,_________不是命题
(1)三角形的三条中线交于一点。
(2)若a>b,则-a<-b。
(3)在△ABC中,若AB=AC,则∠C=∠B吗?
(4)2+3≠5.
(1)(2)(4)
(3)
判断一个句子是不是命题的关键是什么?
是否做出判断
03
新知讲解
1.如果两个三角形的三条边对应相等,那么这两个三角形全等;
2.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行;
3.如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
观察下列命题:
这些命题有什么共同的结构特征?
03
新知讲解
条件
结论
已知事项
由已知事项推断
出来的事项
如果两个三角形的三条边对应相等,那么这两个三角形全等;
命题都可以写成“如果……,那么……”的形式,其中以“如果”开始的部分是条件,“那么”后面的部分是结论.
命题一般由条件和结论两部分组成.
条件是已知事项,结论是由已知事项得到的事项.
新课探究
例1
指出下列命题的条件和结论,并改写成“如果……那么……”的形式.
(1)等底等高的两个三角形面积相等.
(2)对顶角相等。
(3)同位角相等,两直线平行.
03
新知讲解
【例1】指出下列命题的条件和结论,并改写成“如果……那么……”的形式.
(1)等底等高的两个三角形面积相等.
解:(1)这个命题的条件是“两个三角形有一条边和这条边上的高线对应相等”,结论是“这两个三角形的面积相等”,可以改写成“如果两个三角形有一条边和这条边上的高线对应相等,那么这两个三角形的面积相等”.
03
新知讲解
(2)对顶角相等。
相等
对顶角
(两个角是)
条件:
(补上适当词语)
结论:
角
两个
条件:两个角是对顶角,
结论:这两个角相等.
如果两个角是对顶角,那么这两个角相等.
改写:
方法:
先结论,
后条件.
解:(1)
适当增加文字(条件),使语句通畅
03
新知讲解
【例1】指出下列命题的条件和结论,并改写成“如果……那么……”的形式.
(3)同位角相等,两直线平行.
(3)这个命题的条件是“两条直线被第三条直线所截得的同位角相等”,结论是“两直线平行”.可以改写成“如果两条直线被第三条直线所截得的同位角相等,那么这两条直线平行”
03
新知讲解
如果 a=b ,那么 a2=b2。
条件
结论
命题可看做由条件和结论两部分组成。条件是已知事项,结论是由已知事项推出的事项。
命题的组成部分和结构形式:
↖命题组成部分
每一个命题都可以写成“如果…,那么….”的形式,“如果”后的语句是“条件”,“那么”后的语句是“结论”。
↖命题结构形式
03
新知讲解
归纳概念
【总结归纳】
一般地,命题都可以写成“如果……那么……”的形式.其中“如果”引出的部分是条件,“那么”引出的部分是结论.
有些命题没有写成“如果……那么……”的形式,条件和结论不明显,如“同角的余角相等”.对于这样的命题,要经过分析才能找出条件和结论,也可以将它们改写成“如果……那么……”的形式.
04
课堂练习
【知识技能类作业】必做题:
1.下列语句中,属于命题的有( )
①画线段AB=2CM;
②明天早上会下雨;
③直角三角形一定不是轴对称图形;
④如果两个角相等,那么这两个角的补角相等吗?
A.1个 B.2个 C.3个 D.4个
B
04
课堂练习
【知识技能类作业】选做题:
2.下列句子:①直角小于90°;②两点之间,线段最短;
③希望明天下雨;④作AD=BC;
⑤同旁内角互补,两直线平行.
其中是命题的是( )
A.①②③ B.①②⑤
C.①②④⑤ D.①②④
B
04
课堂练习
【综合拓展类作业】
⑵三条边对应相等的两个三角形全等;
这两个三角形全等
两个三角形的三条边对应相等
如果两个三角形有三条边对应相等,那么这两个三角形全等.
⑴和为90°的两个角互为余角。
两个角的和为90°
这两个角互余
如果两个角的和为90°,那么这两个角互余.
条件:
结论:
改写:
3. 找出下列命题的条件和结论,并改写成“如果…那么…”的形式.
条件:
结论:
改写:
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1.把命题“同角的补角相等”改写成“如果……,那么……”的形式,改写正确的是 ( )
A.如果两个角相等,那么这两个角是同一个角的补角
B.如果同角,那么补角相等
C.如果两个角相等,那么这两个角的补角也相等
D.如果两个角是同一个角的补角,那么这两个角相等
【解析】 “同角的补角相等”改写成“如果两个角是同一个角的补角,那么这两个角相等”.
D
06
作业布置
【知识技能类作业】选做题:
2.观察下面四组图形,找出每一组图形的共同特征,并对类似于这样的图形下一个定义.
⑴
⑵
⑶
⑷
如:一个图形由另一个图形改变而来,在改变的过程中保持形状不变(大小可以改变)这个图形和原图形叫做相似图形.
06
作业布置
【综合拓展类作业】
3.在数学运算中,除了加、减、乘、除等运算外,还可以定义新的运算。如定义一种“星”运算,“*”是它的运算符号,其运算法则是:
于是:
按以上定义,填空:
___
___
-5
0
请你参照以上方法,也定义一种新运算,并举几个运算的例子。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 三角形的初步知识
1.2.1 定义与命题
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.了解定义的含义.了解命题的含义.
2.了解命题的结构,会把命题写成“如果……那么……”的形式.
3.通过本节学习,培养树立科学严谨的学习方法.
02
新知导入
小华与小刚正在津津有味地阅读《我们爱科学》.
这个黑客终于被逮住了.
是的,现在的因特网广泛运用于我们的生活中,给我们带来了方便,但…….
这个黑客是个小偷吧?
可能是个喜欢穿黑衣服的贼.
坐在旁边的两个人一边听着他们的谈话,一边也在悄悄地议论着.
03
新知探究
“鸟是动物.”
“鸟是动物吗 ”
这两个句子在叙述上有什么区别
03
新知探究
人们在交流时常需要应用许多名称和术语.为了不产生歧义,对这些名称和术语的含义必须有明确的规定.
如:(1)商店以比原来标价低的价格出售商品叫做 ;
打折
(2)单位体积内所含有某一物质的质量叫做 ;
(3)在同一平面内不相交的两条直线叫 .
密度
平行线
03
新知讲解
03
新知讲解
提炼概念
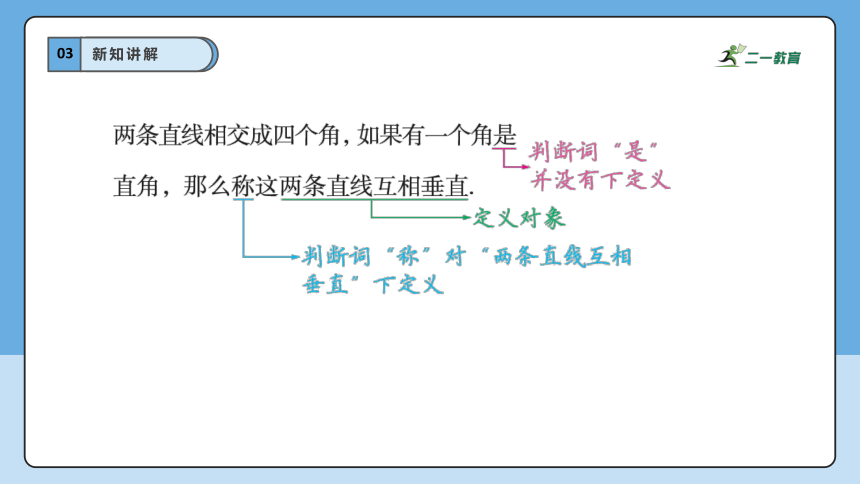
一般地,能清楚地规定某一名称或术语的意义的句子叫做该名称或术语的定义.
下列语句中,属于定义的是( )
A.对顶角相等.
B.三条边对应相等的两个三角形全等.
C.在同一平面内三条线段首尾顺次连接组成的
图形叫做三角形.
D. 同旁内角互补,两直线平行.
C
03
新知讲解
请说出下列名词的定义:
(1)无理数 (2)直角三角形
(3)角平分线 (4)平方根
(1)无限不循环小数是无理数.
(2)有一个角是直角的三角形是直角三角形.
(3)在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的平分线.
(4)一般地,如果一个数的平方等于a,那么这个数叫做a的平方根.
03
新知讲解
比较下列句子在表述形式上,哪些对事情作了判断?哪些没有对事情作出判断?
⑴对顶角相等; ⑵画一个角等于已知角;
⑶两直线平行,同位角相等; ⑷a、b两条直线平行吗?
⑸鸟是动物; ⑹若a2=4,求a的值;
⑺若a2= b2,则a=b; (8)三角形三个内角的和等于1800.
句子_____________ 对事情作了判断;
句子 没有对事情作出判断.
(1)
(3)
(5)
(7)
(2)
(4)
(6)
一般地,判断某一件事情的句子叫做命题.
(8)
命题
不是命题
03
新知讲解
“两只脚的动物是鸡”是不是一个命题呢?
定义是不是
命题呢?
温馨提示:
(1)疑问句和祈使句都不是命题
(2)只需考虑是否作了判断,不需要考虑判断的结果是否正确
03
新知讲解
下列语句中,__________________是命题,_________不是命题
(1)三角形的三条中线交于一点。
(2)若a>b,则-a<-b。
(3)在△ABC中,若AB=AC,则∠C=∠B吗?
(4)2+3≠5.
(1)(2)(4)
(3)
判断一个句子是不是命题的关键是什么?
是否做出判断
03
新知讲解
1.如果两个三角形的三条边对应相等,那么这两个三角形全等;
2.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行;
3.如果一个三角形是等腰三角形,那么这个三角形的两个底角相等.
观察下列命题:
这些命题有什么共同的结构特征?
03
新知讲解
条件
结论
已知事项
由已知事项推断
出来的事项
如果两个三角形的三条边对应相等,那么这两个三角形全等;
命题都可以写成“如果……,那么……”的形式,其中以“如果”开始的部分是条件,“那么”后面的部分是结论.
命题一般由条件和结论两部分组成.
条件是已知事项,结论是由已知事项得到的事项.
新课探究
例1
指出下列命题的条件和结论,并改写成“如果……那么……”的形式.
(1)等底等高的两个三角形面积相等.
(2)对顶角相等。
(3)同位角相等,两直线平行.
03
新知讲解
【例1】指出下列命题的条件和结论,并改写成“如果……那么……”的形式.
(1)等底等高的两个三角形面积相等.
解:(1)这个命题的条件是“两个三角形有一条边和这条边上的高线对应相等”,结论是“这两个三角形的面积相等”,可以改写成“如果两个三角形有一条边和这条边上的高线对应相等,那么这两个三角形的面积相等”.
03
新知讲解
(2)对顶角相等。
相等
对顶角
(两个角是)
条件:
(补上适当词语)
结论:
角
两个
条件:两个角是对顶角,
结论:这两个角相等.
如果两个角是对顶角,那么这两个角相等.
改写:
方法:
先结论,
后条件.
解:(1)
适当增加文字(条件),使语句通畅
03
新知讲解
【例1】指出下列命题的条件和结论,并改写成“如果……那么……”的形式.
(3)同位角相等,两直线平行.
(3)这个命题的条件是“两条直线被第三条直线所截得的同位角相等”,结论是“两直线平行”.可以改写成“如果两条直线被第三条直线所截得的同位角相等,那么这两条直线平行”
03
新知讲解
如果 a=b ,那么 a2=b2。
条件
结论
命题可看做由条件和结论两部分组成。条件是已知事项,结论是由已知事项推出的事项。
命题的组成部分和结构形式:
↖命题组成部分
每一个命题都可以写成“如果…,那么….”的形式,“如果”后的语句是“条件”,“那么”后的语句是“结论”。
↖命题结构形式
03
新知讲解
归纳概念
【总结归纳】
一般地,命题都可以写成“如果……那么……”的形式.其中“如果”引出的部分是条件,“那么”引出的部分是结论.
有些命题没有写成“如果……那么……”的形式,条件和结论不明显,如“同角的余角相等”.对于这样的命题,要经过分析才能找出条件和结论,也可以将它们改写成“如果……那么……”的形式.
04
课堂练习
【知识技能类作业】必做题:
1.下列语句中,属于命题的有( )
①画线段AB=2CM;
②明天早上会下雨;
③直角三角形一定不是轴对称图形;
④如果两个角相等,那么这两个角的补角相等吗?
A.1个 B.2个 C.3个 D.4个
B
04
课堂练习
【知识技能类作业】选做题:
2.下列句子:①直角小于90°;②两点之间,线段最短;
③希望明天下雨;④作AD=BC;
⑤同旁内角互补,两直线平行.
其中是命题的是( )
A.①②③ B.①②⑤
C.①②④⑤ D.①②④
B
04
课堂练习
【综合拓展类作业】
⑵三条边对应相等的两个三角形全等;
这两个三角形全等
两个三角形的三条边对应相等
如果两个三角形有三条边对应相等,那么这两个三角形全等.
⑴和为90°的两个角互为余角。
两个角的和为90°
这两个角互余
如果两个角的和为90°,那么这两个角互余.
条件:
结论:
改写:
3. 找出下列命题的条件和结论,并改写成“如果…那么…”的形式.
条件:
结论:
改写:
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1.把命题“同角的补角相等”改写成“如果……,那么……”的形式,改写正确的是 ( )
A.如果两个角相等,那么这两个角是同一个角的补角
B.如果同角,那么补角相等
C.如果两个角相等,那么这两个角的补角也相等
D.如果两个角是同一个角的补角,那么这两个角相等
【解析】 “同角的补角相等”改写成“如果两个角是同一个角的补角,那么这两个角相等”.
D
06
作业布置
【知识技能类作业】选做题:
2.观察下面四组图形,找出每一组图形的共同特征,并对类似于这样的图形下一个定义.
⑴
⑵
⑶
⑷
如:一个图形由另一个图形改变而来,在改变的过程中保持形状不变(大小可以改变)这个图形和原图形叫做相似图形.
06
作业布置
【综合拓展类作业】
3.在数学运算中,除了加、减、乘、除等运算外,还可以定义新的运算。如定义一种“星”运算,“*”是它的运算符号,其运算法则是:
于是:
按以上定义,填空:
___
___
-5
0
请你参照以上方法,也定义一种新运算,并举几个运算的例子。
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
