2025年浙教版秋期九年级数学上册全册综合试题(含答案)
文档属性
| 名称 | 2025年浙教版秋期九年级数学上册全册综合试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 7.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-13 11:36:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年浙教版秋期九年级数学上册全册综合试题
一、单选题(共10题;共20分)
1.(2分)(2025七下·南山期末)下列说法正确的是( )
A.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件;
B.从1,2,3,4,5中随机抽取一个数,取得偶数的概率为。
C.买一张中国福利彩票,中奖是必然事件:
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次必有1次正面朝上。
2.(2分)(2023九上·息烽月考)某人有红、白、蓝三条长裤和红、白、蓝三件衬衣,他从中任意拿一条长裤和一件衬衣,恰好颜色配套的概率是( )
A. B. C. D.
3.(2分)(2022九上·房县期末)下列事件:①经过有交通信号灯的路口,遇到红灯;②掷一枚均匀的正方体骰子,骰子落地后朝上的点数不是奇数便是偶数;③长为5cm、5cm、11cm的三条线段能围成一个三角形;④买一张体育彩票中奖。其中随机事件有( )
A.1个 B.2个 C.3个 D.4个
4.(2分)(2023九上·金安月考)如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( )
A.40° B.50° C.60° D.70°
5.(2分)(2023九下·青县模拟)如图,直线,直线和被,,所截,,,,则的长为( )
A. B. C. D.
6.(2分)(2025九下·温州开学考)如图是以点为圆心,分别以OA,OB的长为半径的扇面.若,,则阴影部分的面积为( )
A. B. C. D.
7.(2分)(2024·南宁月考)如图①,A,B表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点O是圆心;半径为,点A,B是圆上的两点,,则的长为( )
A. B. C. D.
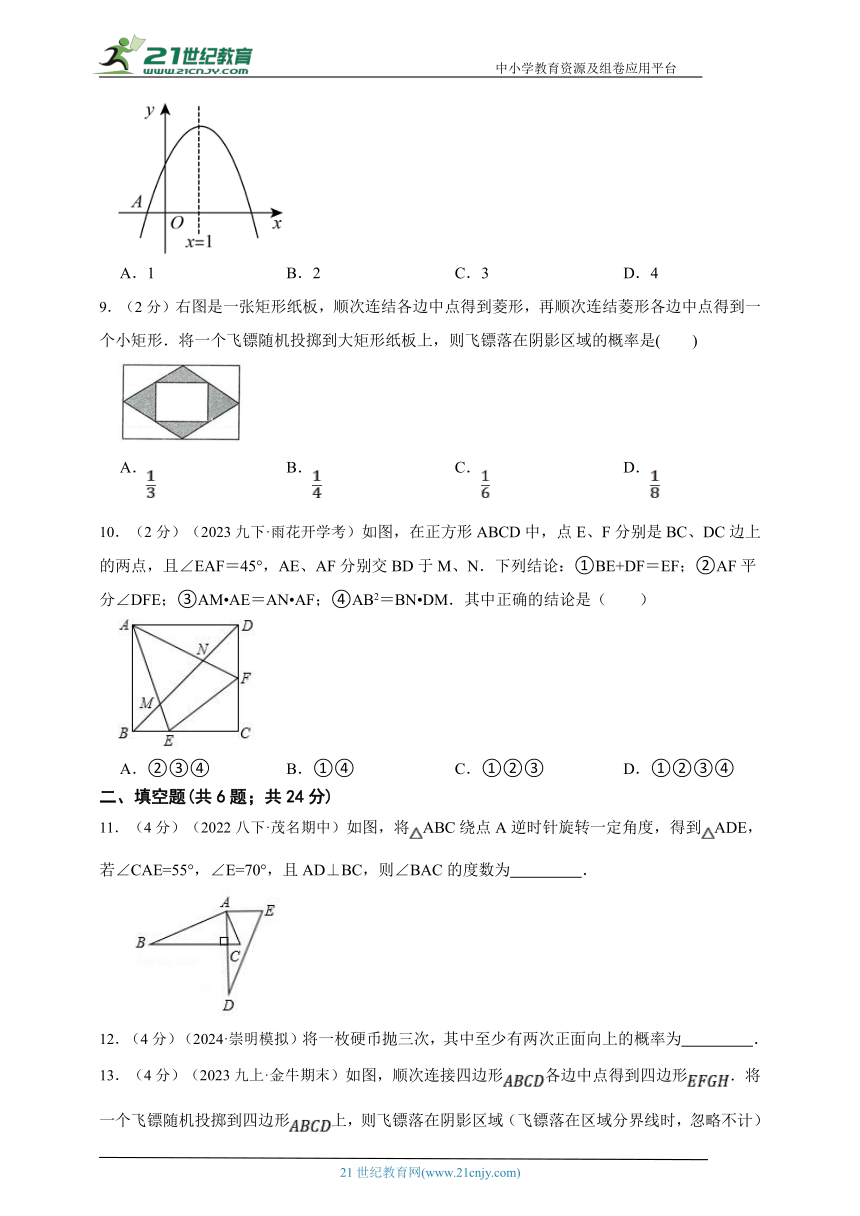
8.(2分)(2023九上·武清月考)如图,已知二次函数的图象与x轴交于点,对称轴为直线,与y轴的交点B在和之间(包括这两点),下列结论:(1)当时,;(2);(3);(4),其中正确的结论有( )个
A.1 B.2 C.3 D.4
9.(2分)右图是一张矩形纸板,顺次连结各边中点得到菱形,再顺次连结菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
A. B. C. D.
10.(2分)(2023九下·雨花开学考)如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M、N.下列结论:①BE+DF=EF;②AF平分∠DFE;③AM AE=AN AF;④AB2=BN DM.其中正确的结论是( )
A.②③④ B.①④ C.①②③ D.①②③④
二、填空题(共6题;共24分)
11.(4分)(2022八下·茂名期中)如图,将ABC绕点A逆时针旋转一定角度,得到ADE,若∠CAE=55°,∠E=70°,且AD⊥BC,则∠BAC的度数为 .
12.(4分)(2024·崇明模拟)将一枚硬币抛三次,其中至少有两次正面向上的概率为 .
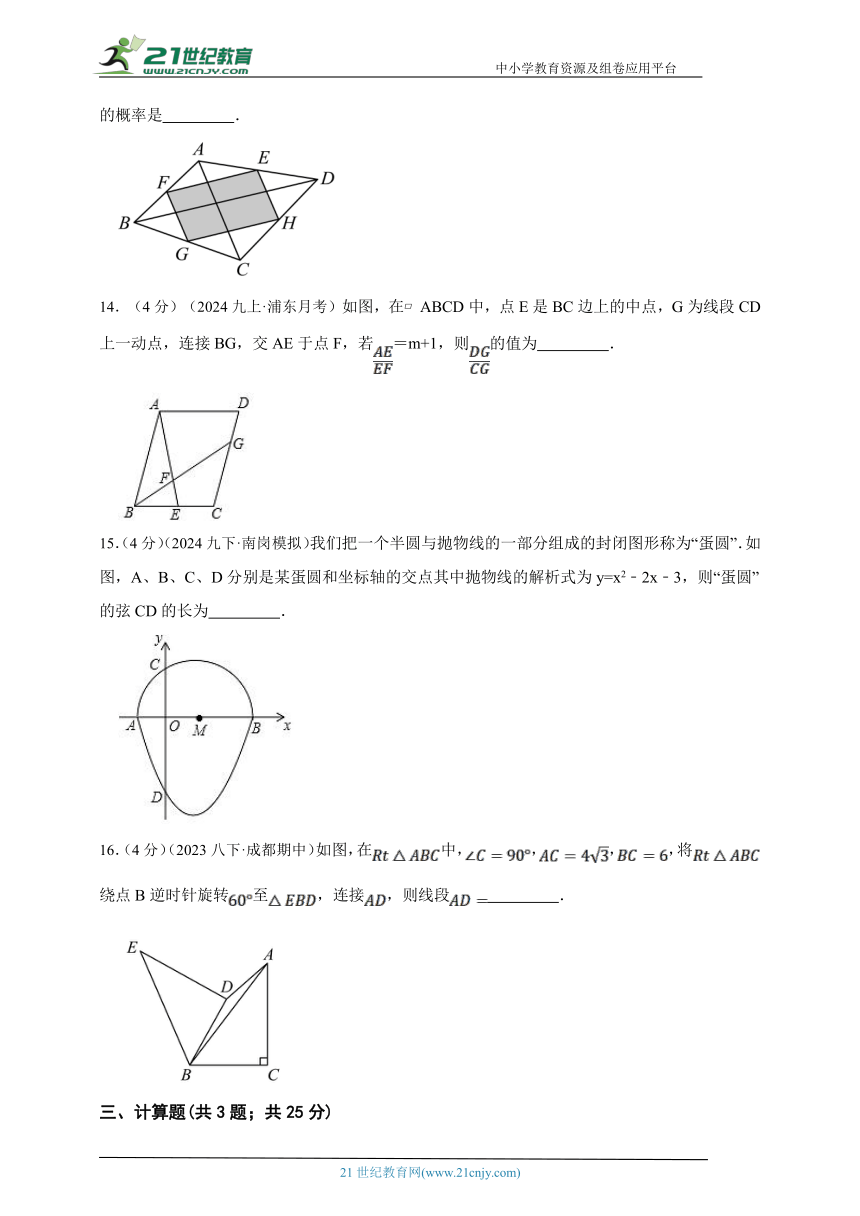
13.(4分)(2023九上·金牛期末)如图,顺次连接四边形各边中点得到四边形.将一个飞镖随机投掷到四边形上,则飞镖落在阴影区域(飞镖落在区域分界线时,忽略不计)的概率是 .
14.(4分)(2024九上·浦东月考)如图,在 ABCD中,点E是BC边上的中点,G为线段CD上一动点,连接BG,交AE于点F,若=m+1,则的值为 .
15.(4分)(2024九下·南岗模拟)我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.如图,A、B、C、D分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y=x2﹣2x﹣3,则“蛋圆”的弦CD的长为 .
16.(4分)(2023八下·成都期中)如图,在中,,,,将绕点B逆时针旋转至,连接,则线段 .
三、计算题(共3题;共25分)
17.(5分)(2023九上·庐江月考)已知二次函数y=x2+6x+k-1(k是常数),如果该二次函数的图象顶点在x轴上,求k的值.
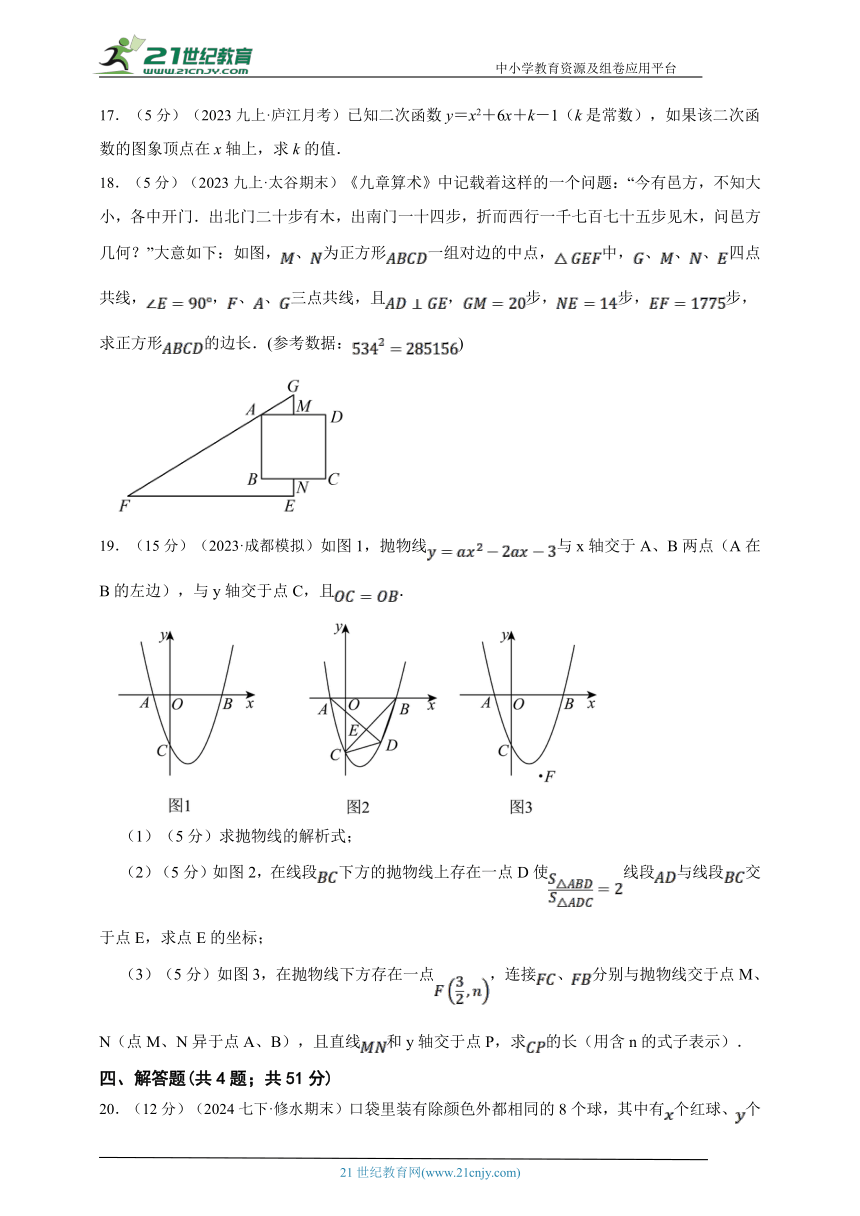
18.(5分)(2023九上·太谷期末)《九章算术》中记载着这样的一个问题:“今有邑方,不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何?”大意如下:如图,、为正方形一组对边的中点,中,、、、四点共线,,、、三点共线,且,步,步,步,求正方形的边长.(参考数据:)
19.(15分)(2023·成都模拟)如图1,抛物线与x轴交于A、B两点(A在B的左边),与y轴交于点C,且.
(1)(5分)求抛物线的解析式;
(2)(5分)如图2,在线段下方的抛物线上存在一点D使线段与线段交于点E,求点E的坐标;
(3)(5分)如图3,在抛物线下方存在一点,连接、分别与抛物线交于点M、N(点M、N异于点A、B),且直线和y轴交于点P,求的长(用含n的式子表示).
四、解答题(共4题;共51分)
20.(12分)(2024七下·修水期末)口袋里装有除颜色外都相同的8个球,其中有个红球、个白球,没有其他颜色的球,从中随意摸出一个球.
(1)(6分)如果摸到红球与摸到白球的可能性相等,分别求和的值.
(2)(6分)在(1)的条件下,现从袋中取走若干白球,并放入相同数目的红球,搅拌均匀后,再从袋中随意摸出一个球是红球的概率是,求取走了多少个白球.
21.(12分)(2024九上·晋城期末)已知二次函数.
(1)(6分)求该函数图象的顶点坐标和对称轴.
(2)(6分)自变量x在什么范围内时,y随x的增大而增大.
22.(6分)(2023九上·德惠月考)两枚质地均匀的正方体骰子,六个面上的点数分别为1,2,3,4,5,6, 同时抛掷这两枚骰子一次,求朝上的面的点数之和为5或9的概率.
23.(21分)(2023九上·吴兴期中)如图所示,抛物线与双曲线相交于点A、B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴距离的4倍,记抛物线的顶点为E。
(1)(7分)求双曲线和抛物线的函数关系式;
(2)(6分)计算△ABC与△ABE的面积;
(3)(8分)在抛物线上是否存在点D,使 ABD的面积等于 ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由。
答案解析部分
1.【答案】A
【知识点】事件的分类;简单事件概率的计算
2.【答案】C
【知识点】用列表法或树状图法求概率
3.【答案】B
【知识点】事件的分类
4.【答案】C
【知识点】旋转的性质
5.【答案】D
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】D
【知识点】扇形面积的计算
7.【答案】B
【知识点】弧长的计算
8.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
9.【答案】B
【知识点】几何概率
10.【答案】D
【知识点】正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
11.【答案】85°
【知识点】旋转的性质
12.【答案】
【知识点】用列表法或树状图法求概率;概率公式
13.【答案】
【知识点】相似三角形的判定与性质;几何概率;三角形的中位线定理
14.【答案】
【知识点】相似三角形的性质;相似三角形的判定
15.【答案】3+
【知识点】二次函数图象与坐标轴的交点问题;勾股定理
16.【答案】
【知识点】等边三角形的性质;勾股定理;旋转的性质
17.【答案】解:根据题意,得,
解得k=10
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax²+bx+c的性质
18.【答案】正方形小城的边长为步
【知识点】相似三角形的判定与性质
19.【答案】(1)
(2)
(3)
【知识点】待定系数法求二次函数解析式;平行线的判定与性质;相似三角形的判定与性质
20.【答案】(1)解:∵摸到红球与摸到白球的可能性相等,
∴x=y
∵x+y=8
∴x=y=4
(2)解:设取走个白球,放入个红球,则口袋中现在有白球个、红球个,根据题意得,
解得.
答:取走了3个白球.
【知识点】概率公式;简单事件概率的计算
21.【答案】(1)该函数图象的顶点坐标为,对称轴为直线
(2)当时,y随x的增大而增大
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
22.【答案】解:
【知识点】概率公式
23.【答案】(1)解:将点 ,点A(-2,2)代入 双曲线 ,可得:解得:双曲线解析式.又因为 直线BC与x轴之间的距离是点B到y轴距离的4倍 ,且点B在第四象限内,所以可设点B的坐标为在将点B代入双曲线解析式得:解得:(舍去),则点B的坐标为(1,-4),因为抛物线的图像过点A(-2,2)、点B(1,-4),点O(0,0)可得:解得:所以抛物线解析式为
(2)解:由题意可得点C的纵坐标为-4,则解得:则点C的坐标为:,点A(-2,2)、点B(1,-4),所以
因为抛物线解析式为则点E设直线AB的解析式为:将点A(-2,2)、点B(1,-4)代入得:解得:即直线AB的解析式为:设直线AB与抛物线对称轴相交于点F,设点F的坐标为则所以
所以.
(3)解:由(2)知,所以当点D的坐标与C点重合时,满足题意,此时点D(-4,-4).根据平行线之间距离相等,过点C作AB的平行线CD,可设直线CD的解析式为:将点C坐标代入得:解得g=12,即直线CD的解析式为:,则点D为直线CD与抛物线的交点,联立直线CD与抛物线的解析式并消去y得:解得:(舍去),当x=3时,y=18,此时点D坐标为(3,-18),综上所述:点D坐标为:(-4,-4),(3,-18).
【知识点】二次函数的实际应用-几何问题;反比例函数-动态几何问题
2025年浙教版秋期九年级数学上册全册综合试题
一、单选题(共10题;共20分)
1.(2分)(2025七下·南山期末)下列说法正确的是( )
A.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件;
B.从1,2,3,4,5中随机抽取一个数,取得偶数的概率为。
C.买一张中国福利彩票,中奖是必然事件:
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次必有1次正面朝上。
2.(2分)(2023九上·息烽月考)某人有红、白、蓝三条长裤和红、白、蓝三件衬衣,他从中任意拿一条长裤和一件衬衣,恰好颜色配套的概率是( )
A. B. C. D.
3.(2分)(2022九上·房县期末)下列事件:①经过有交通信号灯的路口,遇到红灯;②掷一枚均匀的正方体骰子,骰子落地后朝上的点数不是奇数便是偶数;③长为5cm、5cm、11cm的三条线段能围成一个三角形;④买一张体育彩票中奖。其中随机事件有( )
A.1个 B.2个 C.3个 D.4个
4.(2分)(2023九上·金安月考)如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( )
A.40° B.50° C.60° D.70°
5.(2分)(2023九下·青县模拟)如图,直线,直线和被,,所截,,,,则的长为( )
A. B. C. D.
6.(2分)(2025九下·温州开学考)如图是以点为圆心,分别以OA,OB的长为半径的扇面.若,,则阴影部分的面积为( )
A. B. C. D.
7.(2分)(2024·南宁月考)如图①,A,B表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点O是圆心;半径为,点A,B是圆上的两点,,则的长为( )
A. B. C. D.
8.(2分)(2023九上·武清月考)如图,已知二次函数的图象与x轴交于点,对称轴为直线,与y轴的交点B在和之间(包括这两点),下列结论:(1)当时,;(2);(3);(4),其中正确的结论有( )个
A.1 B.2 C.3 D.4
9.(2分)右图是一张矩形纸板,顺次连结各边中点得到菱形,再顺次连结菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
A. B. C. D.
10.(2分)(2023九下·雨花开学考)如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M、N.下列结论:①BE+DF=EF;②AF平分∠DFE;③AM AE=AN AF;④AB2=BN DM.其中正确的结论是( )
A.②③④ B.①④ C.①②③ D.①②③④
二、填空题(共6题;共24分)
11.(4分)(2022八下·茂名期中)如图,将ABC绕点A逆时针旋转一定角度,得到ADE,若∠CAE=55°,∠E=70°,且AD⊥BC,则∠BAC的度数为 .
12.(4分)(2024·崇明模拟)将一枚硬币抛三次,其中至少有两次正面向上的概率为 .
13.(4分)(2023九上·金牛期末)如图,顺次连接四边形各边中点得到四边形.将一个飞镖随机投掷到四边形上,则飞镖落在阴影区域(飞镖落在区域分界线时,忽略不计)的概率是 .
14.(4分)(2024九上·浦东月考)如图,在 ABCD中,点E是BC边上的中点,G为线段CD上一动点,连接BG,交AE于点F,若=m+1,则的值为 .
15.(4分)(2024九下·南岗模拟)我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.如图,A、B、C、D分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y=x2﹣2x﹣3,则“蛋圆”的弦CD的长为 .
16.(4分)(2023八下·成都期中)如图,在中,,,,将绕点B逆时针旋转至,连接,则线段 .
三、计算题(共3题;共25分)
17.(5分)(2023九上·庐江月考)已知二次函数y=x2+6x+k-1(k是常数),如果该二次函数的图象顶点在x轴上,求k的值.
18.(5分)(2023九上·太谷期末)《九章算术》中记载着这样的一个问题:“今有邑方,不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何?”大意如下:如图,、为正方形一组对边的中点,中,、、、四点共线,,、、三点共线,且,步,步,步,求正方形的边长.(参考数据:)
19.(15分)(2023·成都模拟)如图1,抛物线与x轴交于A、B两点(A在B的左边),与y轴交于点C,且.
(1)(5分)求抛物线的解析式;
(2)(5分)如图2,在线段下方的抛物线上存在一点D使线段与线段交于点E,求点E的坐标;
(3)(5分)如图3,在抛物线下方存在一点,连接、分别与抛物线交于点M、N(点M、N异于点A、B),且直线和y轴交于点P,求的长(用含n的式子表示).
四、解答题(共4题;共51分)
20.(12分)(2024七下·修水期末)口袋里装有除颜色外都相同的8个球,其中有个红球、个白球,没有其他颜色的球,从中随意摸出一个球.
(1)(6分)如果摸到红球与摸到白球的可能性相等,分别求和的值.
(2)(6分)在(1)的条件下,现从袋中取走若干白球,并放入相同数目的红球,搅拌均匀后,再从袋中随意摸出一个球是红球的概率是,求取走了多少个白球.
21.(12分)(2024九上·晋城期末)已知二次函数.
(1)(6分)求该函数图象的顶点坐标和对称轴.
(2)(6分)自变量x在什么范围内时,y随x的增大而增大.
22.(6分)(2023九上·德惠月考)两枚质地均匀的正方体骰子,六个面上的点数分别为1,2,3,4,5,6, 同时抛掷这两枚骰子一次,求朝上的面的点数之和为5或9的概率.
23.(21分)(2023九上·吴兴期中)如图所示,抛物线与双曲线相交于点A、B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴距离的4倍,记抛物线的顶点为E。
(1)(7分)求双曲线和抛物线的函数关系式;
(2)(6分)计算△ABC与△ABE的面积;
(3)(8分)在抛物线上是否存在点D,使 ABD的面积等于 ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由。
答案解析部分
1.【答案】A
【知识点】事件的分类;简单事件概率的计算
2.【答案】C
【知识点】用列表法或树状图法求概率
3.【答案】B
【知识点】事件的分类
4.【答案】C
【知识点】旋转的性质
5.【答案】D
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】D
【知识点】扇形面积的计算
7.【答案】B
【知识点】弧长的计算
8.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
9.【答案】B
【知识点】几何概率
10.【答案】D
【知识点】正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
11.【答案】85°
【知识点】旋转的性质
12.【答案】
【知识点】用列表法或树状图法求概率;概率公式
13.【答案】
【知识点】相似三角形的判定与性质;几何概率;三角形的中位线定理
14.【答案】
【知识点】相似三角形的性质;相似三角形的判定
15.【答案】3+
【知识点】二次函数图象与坐标轴的交点问题;勾股定理
16.【答案】
【知识点】等边三角形的性质;勾股定理;旋转的性质
17.【答案】解:根据题意,得,
解得k=10
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax²+bx+c的性质
18.【答案】正方形小城的边长为步
【知识点】相似三角形的判定与性质
19.【答案】(1)
(2)
(3)
【知识点】待定系数法求二次函数解析式;平行线的判定与性质;相似三角形的判定与性质
20.【答案】(1)解:∵摸到红球与摸到白球的可能性相等,
∴x=y
∵x+y=8
∴x=y=4
(2)解:设取走个白球,放入个红球,则口袋中现在有白球个、红球个,根据题意得,
解得.
答:取走了3个白球.
【知识点】概率公式;简单事件概率的计算
21.【答案】(1)该函数图象的顶点坐标为,对称轴为直线
(2)当时,y随x的增大而增大
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
22.【答案】解:
【知识点】概率公式
23.【答案】(1)解:将点 ,点A(-2,2)代入 双曲线 ,可得:解得:双曲线解析式.又因为 直线BC与x轴之间的距离是点B到y轴距离的4倍 ,且点B在第四象限内,所以可设点B的坐标为在将点B代入双曲线解析式得:解得:(舍去),则点B的坐标为(1,-4),因为抛物线的图像过点A(-2,2)、点B(1,-4),点O(0,0)可得:解得:所以抛物线解析式为
(2)解:由题意可得点C的纵坐标为-4,则解得:则点C的坐标为:,点A(-2,2)、点B(1,-4),所以
因为抛物线解析式为则点E设直线AB的解析式为:将点A(-2,2)、点B(1,-4)代入得:解得:即直线AB的解析式为:设直线AB与抛物线对称轴相交于点F,设点F的坐标为则所以
所以.
(3)解:由(2)知,所以当点D的坐标与C点重合时,满足题意,此时点D(-4,-4).根据平行线之间距离相等,过点C作AB的平行线CD,可设直线CD的解析式为:将点C坐标代入得:解得g=12,即直线CD的解析式为:,则点D为直线CD与抛物线的交点,联立直线CD与抛物线的解析式并消去y得:解得:(舍去),当x=3时,y=18,此时点D坐标为(3,-18),综上所述:点D坐标为:(-4,-4),(3,-18).
【知识点】二次函数的实际应用-几何问题;反比例函数-动态几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2025年浙教版秋期九年级数学上册全册综合试题
一、单选题(共10题;共20分)
1.(2分)(2025七下·南山期末)下列说法正确的是( )
A.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件;
B.从1,2,3,4,5中随机抽取一个数,取得偶数的概率为。
C.买一张中国福利彩票,中奖是必然事件:
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次必有1次正面朝上。
2.(2分)(2023九上·息烽月考)某人有红、白、蓝三条长裤和红、白、蓝三件衬衣,他从中任意拿一条长裤和一件衬衣,恰好颜色配套的概率是( )
A. B. C. D.
3.(2分)(2022九上·房县期末)下列事件:①经过有交通信号灯的路口,遇到红灯;②掷一枚均匀的正方体骰子,骰子落地后朝上的点数不是奇数便是偶数;③长为5cm、5cm、11cm的三条线段能围成一个三角形;④买一张体育彩票中奖。其中随机事件有( )
A.1个 B.2个 C.3个 D.4个
4.(2分)(2023九上·金安月考)如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( )
A.40° B.50° C.60° D.70°
5.(2分)(2023九下·青县模拟)如图,直线,直线和被,,所截,,,,则的长为( )
A. B. C. D.
6.(2分)(2025九下·温州开学考)如图是以点为圆心,分别以OA,OB的长为半径的扇面.若,,则阴影部分的面积为( )
A. B. C. D.
7.(2分)(2024·南宁月考)如图①,A,B表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点O是圆心;半径为,点A,B是圆上的两点,,则的长为( )
A. B. C. D.
8.(2分)(2023九上·武清月考)如图,已知二次函数的图象与x轴交于点,对称轴为直线,与y轴的交点B在和之间(包括这两点),下列结论:(1)当时,;(2);(3);(4),其中正确的结论有( )个
A.1 B.2 C.3 D.4
9.(2分)右图是一张矩形纸板,顺次连结各边中点得到菱形,再顺次连结菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
A. B. C. D.
10.(2分)(2023九下·雨花开学考)如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M、N.下列结论:①BE+DF=EF;②AF平分∠DFE;③AM AE=AN AF;④AB2=BN DM.其中正确的结论是( )
A.②③④ B.①④ C.①②③ D.①②③④
二、填空题(共6题;共24分)
11.(4分)(2022八下·茂名期中)如图,将ABC绕点A逆时针旋转一定角度,得到ADE,若∠CAE=55°,∠E=70°,且AD⊥BC,则∠BAC的度数为 .
12.(4分)(2024·崇明模拟)将一枚硬币抛三次,其中至少有两次正面向上的概率为 .
13.(4分)(2023九上·金牛期末)如图,顺次连接四边形各边中点得到四边形.将一个飞镖随机投掷到四边形上,则飞镖落在阴影区域(飞镖落在区域分界线时,忽略不计)的概率是 .
14.(4分)(2024九上·浦东月考)如图,在 ABCD中,点E是BC边上的中点,G为线段CD上一动点,连接BG,交AE于点F,若=m+1,则的值为 .
15.(4分)(2024九下·南岗模拟)我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.如图,A、B、C、D分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y=x2﹣2x﹣3,则“蛋圆”的弦CD的长为 .
16.(4分)(2023八下·成都期中)如图,在中,,,,将绕点B逆时针旋转至,连接,则线段 .
三、计算题(共3题;共25分)
17.(5分)(2023九上·庐江月考)已知二次函数y=x2+6x+k-1(k是常数),如果该二次函数的图象顶点在x轴上,求k的值.
18.(5分)(2023九上·太谷期末)《九章算术》中记载着这样的一个问题:“今有邑方,不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何?”大意如下:如图,、为正方形一组对边的中点,中,、、、四点共线,,、、三点共线,且,步,步,步,求正方形的边长.(参考数据:)
19.(15分)(2023·成都模拟)如图1,抛物线与x轴交于A、B两点(A在B的左边),与y轴交于点C,且.
(1)(5分)求抛物线的解析式;
(2)(5分)如图2,在线段下方的抛物线上存在一点D使线段与线段交于点E,求点E的坐标;
(3)(5分)如图3,在抛物线下方存在一点,连接、分别与抛物线交于点M、N(点M、N异于点A、B),且直线和y轴交于点P,求的长(用含n的式子表示).
四、解答题(共4题;共51分)
20.(12分)(2024七下·修水期末)口袋里装有除颜色外都相同的8个球,其中有个红球、个白球,没有其他颜色的球,从中随意摸出一个球.
(1)(6分)如果摸到红球与摸到白球的可能性相等,分别求和的值.
(2)(6分)在(1)的条件下,现从袋中取走若干白球,并放入相同数目的红球,搅拌均匀后,再从袋中随意摸出一个球是红球的概率是,求取走了多少个白球.
21.(12分)(2024九上·晋城期末)已知二次函数.
(1)(6分)求该函数图象的顶点坐标和对称轴.
(2)(6分)自变量x在什么范围内时,y随x的增大而增大.
22.(6分)(2023九上·德惠月考)两枚质地均匀的正方体骰子,六个面上的点数分别为1,2,3,4,5,6, 同时抛掷这两枚骰子一次,求朝上的面的点数之和为5或9的概率.
23.(21分)(2023九上·吴兴期中)如图所示,抛物线与双曲线相交于点A、B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴距离的4倍,记抛物线的顶点为E。
(1)(7分)求双曲线和抛物线的函数关系式;
(2)(6分)计算△ABC与△ABE的面积;
(3)(8分)在抛物线上是否存在点D,使 ABD的面积等于 ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由。
答案解析部分
1.【答案】A
【知识点】事件的分类;简单事件概率的计算
2.【答案】C
【知识点】用列表法或树状图法求概率
3.【答案】B
【知识点】事件的分类
4.【答案】C
【知识点】旋转的性质
5.【答案】D
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】D
【知识点】扇形面积的计算
7.【答案】B
【知识点】弧长的计算
8.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
9.【答案】B
【知识点】几何概率
10.【答案】D
【知识点】正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
11.【答案】85°
【知识点】旋转的性质
12.【答案】
【知识点】用列表法或树状图法求概率;概率公式
13.【答案】
【知识点】相似三角形的判定与性质;几何概率;三角形的中位线定理
14.【答案】
【知识点】相似三角形的性质;相似三角形的判定
15.【答案】3+
【知识点】二次函数图象与坐标轴的交点问题;勾股定理
16.【答案】
【知识点】等边三角形的性质;勾股定理;旋转的性质
17.【答案】解:根据题意,得,
解得k=10
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax²+bx+c的性质
18.【答案】正方形小城的边长为步
【知识点】相似三角形的判定与性质
19.【答案】(1)
(2)
(3)
【知识点】待定系数法求二次函数解析式;平行线的判定与性质;相似三角形的判定与性质
20.【答案】(1)解:∵摸到红球与摸到白球的可能性相等,
∴x=y
∵x+y=8
∴x=y=4
(2)解:设取走个白球,放入个红球,则口袋中现在有白球个、红球个,根据题意得,
解得.
答:取走了3个白球.
【知识点】概率公式;简单事件概率的计算
21.【答案】(1)该函数图象的顶点坐标为,对称轴为直线
(2)当时,y随x的增大而增大
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
22.【答案】解:
【知识点】概率公式
23.【答案】(1)解:将点 ,点A(-2,2)代入 双曲线 ,可得:解得:双曲线解析式.又因为 直线BC与x轴之间的距离是点B到y轴距离的4倍 ,且点B在第四象限内,所以可设点B的坐标为在将点B代入双曲线解析式得:解得:(舍去),则点B的坐标为(1,-4),因为抛物线的图像过点A(-2,2)、点B(1,-4),点O(0,0)可得:解得:所以抛物线解析式为
(2)解:由题意可得点C的纵坐标为-4,则解得:则点C的坐标为:,点A(-2,2)、点B(1,-4),所以
因为抛物线解析式为则点E设直线AB的解析式为:将点A(-2,2)、点B(1,-4)代入得:解得:即直线AB的解析式为:设直线AB与抛物线对称轴相交于点F,设点F的坐标为则所以
所以.
(3)解:由(2)知,所以当点D的坐标与C点重合时,满足题意,此时点D(-4,-4).根据平行线之间距离相等,过点C作AB的平行线CD,可设直线CD的解析式为:将点C坐标代入得:解得g=12,即直线CD的解析式为:,则点D为直线CD与抛物线的交点,联立直线CD与抛物线的解析式并消去y得:解得:(舍去),当x=3时,y=18,此时点D坐标为(3,-18),综上所述:点D坐标为:(-4,-4),(3,-18).
【知识点】二次函数的实际应用-几何问题;反比例函数-动态几何问题
2025年浙教版秋期九年级数学上册全册综合试题
一、单选题(共10题;共20分)
1.(2分)(2025七下·南山期末)下列说法正确的是( )
A.小强一次掷出3颗质地均匀的骰子,3颗全是6点朝上是随机事件;
B.从1,2,3,4,5中随机抽取一个数,取得偶数的概率为。
C.买一张中国福利彩票,中奖是必然事件:
D.抛一枚质地均匀的硬币,正面朝上的概率为,连续抛此硬币2次必有1次正面朝上。
2.(2分)(2023九上·息烽月考)某人有红、白、蓝三条长裤和红、白、蓝三件衬衣,他从中任意拿一条长裤和一件衬衣,恰好颜色配套的概率是( )
A. B. C. D.
3.(2分)(2022九上·房县期末)下列事件:①经过有交通信号灯的路口,遇到红灯;②掷一枚均匀的正方体骰子,骰子落地后朝上的点数不是奇数便是偶数;③长为5cm、5cm、11cm的三条线段能围成一个三角形;④买一张体育彩票中奖。其中随机事件有( )
A.1个 B.2个 C.3个 D.4个
4.(2分)(2023九上·金安月考)如图,△COD是△AOB绕点O顺时针旋转40°后得到的图形,若点C恰好落在AB上,且∠AOD的度数为90°,则∠B的度数是( )
A.40° B.50° C.60° D.70°
5.(2分)(2023九下·青县模拟)如图,直线,直线和被,,所截,,,,则的长为( )
A. B. C. D.
6.(2分)(2025九下·温州开学考)如图是以点为圆心,分别以OA,OB的长为半径的扇面.若,,则阴影部分的面积为( )
A. B. C. D.
7.(2分)(2024·南宁月考)如图①,A,B表示某游乐场摩天轮上的两个轿厢.图②是其示意图,点O是圆心;半径为,点A,B是圆上的两点,,则的长为( )
A. B. C. D.
8.(2分)(2023九上·武清月考)如图,已知二次函数的图象与x轴交于点,对称轴为直线,与y轴的交点B在和之间(包括这两点),下列结论:(1)当时,;(2);(3);(4),其中正确的结论有( )个
A.1 B.2 C.3 D.4
9.(2分)右图是一张矩形纸板,顺次连结各边中点得到菱形,再顺次连结菱形各边中点得到一个小矩形.将一个飞镖随机投掷到大矩形纸板上,则飞镖落在阴影区域的概率是( )
A. B. C. D.
10.(2分)(2023九下·雨花开学考)如图,在正方形ABCD中,点E、F分别是BC、DC边上的两点,且∠EAF=45°,AE、AF分别交BD于M、N.下列结论:①BE+DF=EF;②AF平分∠DFE;③AM AE=AN AF;④AB2=BN DM.其中正确的结论是( )
A.②③④ B.①④ C.①②③ D.①②③④
二、填空题(共6题;共24分)
11.(4分)(2022八下·茂名期中)如图,将ABC绕点A逆时针旋转一定角度,得到ADE,若∠CAE=55°,∠E=70°,且AD⊥BC,则∠BAC的度数为 .
12.(4分)(2024·崇明模拟)将一枚硬币抛三次,其中至少有两次正面向上的概率为 .
13.(4分)(2023九上·金牛期末)如图,顺次连接四边形各边中点得到四边形.将一个飞镖随机投掷到四边形上,则飞镖落在阴影区域(飞镖落在区域分界线时,忽略不计)的概率是 .
14.(4分)(2024九上·浦东月考)如图,在 ABCD中,点E是BC边上的中点,G为线段CD上一动点,连接BG,交AE于点F,若=m+1,则的值为 .
15.(4分)(2024九下·南岗模拟)我们把一个半圆与抛物线的一部分组成的封闭图形称为“蛋圆”.如图,A、B、C、D分别是某蛋圆和坐标轴的交点其中抛物线的解析式为y=x2﹣2x﹣3,则“蛋圆”的弦CD的长为 .
16.(4分)(2023八下·成都期中)如图,在中,,,,将绕点B逆时针旋转至,连接,则线段 .
三、计算题(共3题;共25分)
17.(5分)(2023九上·庐江月考)已知二次函数y=x2+6x+k-1(k是常数),如果该二次函数的图象顶点在x轴上,求k的值.
18.(5分)(2023九上·太谷期末)《九章算术》中记载着这样的一个问题:“今有邑方,不知大小,各中开门.出北门二十步有木,出南门一十四步,折而西行一千七百七十五步见木,问邑方几何?”大意如下:如图,、为正方形一组对边的中点,中,、、、四点共线,,、、三点共线,且,步,步,步,求正方形的边长.(参考数据:)
19.(15分)(2023·成都模拟)如图1,抛物线与x轴交于A、B两点(A在B的左边),与y轴交于点C,且.
(1)(5分)求抛物线的解析式;
(2)(5分)如图2,在线段下方的抛物线上存在一点D使线段与线段交于点E,求点E的坐标;
(3)(5分)如图3,在抛物线下方存在一点,连接、分别与抛物线交于点M、N(点M、N异于点A、B),且直线和y轴交于点P,求的长(用含n的式子表示).
四、解答题(共4题;共51分)
20.(12分)(2024七下·修水期末)口袋里装有除颜色外都相同的8个球,其中有个红球、个白球,没有其他颜色的球,从中随意摸出一个球.
(1)(6分)如果摸到红球与摸到白球的可能性相等,分别求和的值.
(2)(6分)在(1)的条件下,现从袋中取走若干白球,并放入相同数目的红球,搅拌均匀后,再从袋中随意摸出一个球是红球的概率是,求取走了多少个白球.
21.(12分)(2024九上·晋城期末)已知二次函数.
(1)(6分)求该函数图象的顶点坐标和对称轴.
(2)(6分)自变量x在什么范围内时,y随x的增大而增大.
22.(6分)(2023九上·德惠月考)两枚质地均匀的正方体骰子,六个面上的点数分别为1,2,3,4,5,6, 同时抛掷这两枚骰子一次,求朝上的面的点数之和为5或9的概率.
23.(21分)(2023九上·吴兴期中)如图所示,抛物线与双曲线相交于点A、B,且抛物线经过坐标原点,点A的坐标为(-2,2),点B在第四象限内,过点B作直线BC∥x轴,C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴距离的4倍,记抛物线的顶点为E。
(1)(7分)求双曲线和抛物线的函数关系式;
(2)(6分)计算△ABC与△ABE的面积;
(3)(8分)在抛物线上是否存在点D,使 ABD的面积等于 ABE的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由。
答案解析部分
1.【答案】A
【知识点】事件的分类;简单事件概率的计算
2.【答案】C
【知识点】用列表法或树状图法求概率
3.【答案】B
【知识点】事件的分类
4.【答案】C
【知识点】旋转的性质
5.【答案】D
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
6.【答案】D
【知识点】扇形面积的计算
7.【答案】B
【知识点】弧长的计算
8.【答案】C
【知识点】二次函数图象与系数的关系;二次函数图象与坐标轴的交点问题
9.【答案】B
【知识点】几何概率
10.【答案】D
【知识点】正方形的性质;相似三角形的判定与性质;三角形全等的判定-SAS
11.【答案】85°
【知识点】旋转的性质
12.【答案】
【知识点】用列表法或树状图法求概率;概率公式
13.【答案】
【知识点】相似三角形的判定与性质;几何概率;三角形的中位线定理
14.【答案】
【知识点】相似三角形的性质;相似三角形的判定
15.【答案】3+
【知识点】二次函数图象与坐标轴的交点问题;勾股定理
16.【答案】
【知识点】等边三角形的性质;勾股定理;旋转的性质
17.【答案】解:根据题意,得,
解得k=10
【知识点】二次函数图象与坐标轴的交点问题;二次函数y=ax²+bx+c的性质
18.【答案】正方形小城的边长为步
【知识点】相似三角形的判定与性质
19.【答案】(1)
(2)
(3)
【知识点】待定系数法求二次函数解析式;平行线的判定与性质;相似三角形的判定与性质
20.【答案】(1)解:∵摸到红球与摸到白球的可能性相等,
∴x=y
∵x+y=8
∴x=y=4
(2)解:设取走个白球,放入个红球,则口袋中现在有白球个、红球个,根据题意得,
解得.
答:取走了3个白球.
【知识点】概率公式;简单事件概率的计算
21.【答案】(1)该函数图象的顶点坐标为,对称轴为直线
(2)当时,y随x的增大而增大
【知识点】二次函数y=ax²+bx+c与二次函数y=a(x-h)²+k的转化
22.【答案】解:
【知识点】概率公式
23.【答案】(1)解:将点 ,点A(-2,2)代入 双曲线 ,可得:解得:双曲线解析式.又因为 直线BC与x轴之间的距离是点B到y轴距离的4倍 ,且点B在第四象限内,所以可设点B的坐标为在将点B代入双曲线解析式得:解得:(舍去),则点B的坐标为(1,-4),因为抛物线的图像过点A(-2,2)、点B(1,-4),点O(0,0)可得:解得:所以抛物线解析式为
(2)解:由题意可得点C的纵坐标为-4,则解得:则点C的坐标为:,点A(-2,2)、点B(1,-4),所以
因为抛物线解析式为则点E设直线AB的解析式为:将点A(-2,2)、点B(1,-4)代入得:解得:即直线AB的解析式为:设直线AB与抛物线对称轴相交于点F,设点F的坐标为则所以
所以.
(3)解:由(2)知,所以当点D的坐标与C点重合时,满足题意,此时点D(-4,-4).根据平行线之间距离相等,过点C作AB的平行线CD,可设直线CD的解析式为:将点C坐标代入得:解得g=12,即直线CD的解析式为:,则点D为直线CD与抛物线的交点,联立直线CD与抛物线的解析式并消去y得:解得:(舍去),当x=3时,y=18,此时点D坐标为(3,-18),综上所述:点D坐标为:(-4,-4),(3,-18).
【知识点】二次函数的实际应用-几何问题;反比例函数-动态几何问题
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
