2.3 等腰三角形的性质定理(1) 课件(共23张PPT)
文档属性
| 名称 | 2.3 等腰三角形的性质定理(1) 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-16 09:01:43 | ||
图片预览

文档简介
(共23张PPT)
2.3 等腰三角形的性质(1)
浙教版八年级上册
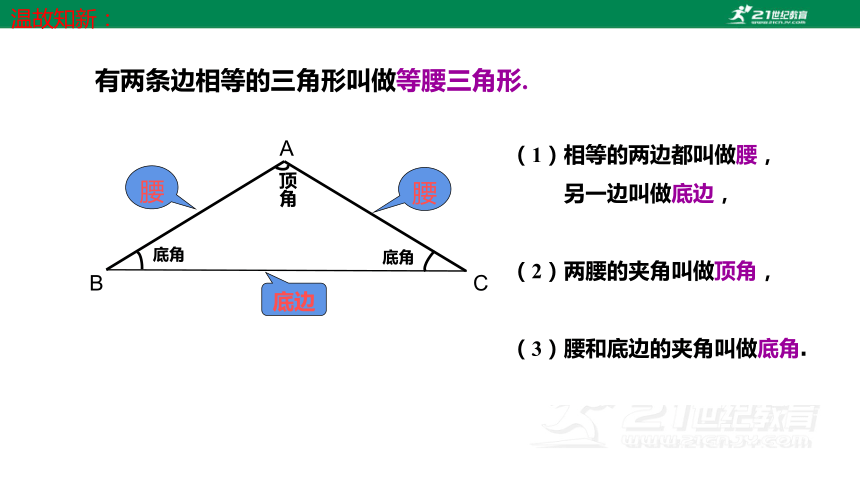
有两条边相等的三角形叫做等腰三角形.
(1)相等的两边都叫做腰,
另一边叫做底边,
(2)两腰的夹角叫做顶角,
(3)腰和底边的夹角叫做底角.
腰
腰
底边
顶角
底角
底角
A
B
C
温故知新:
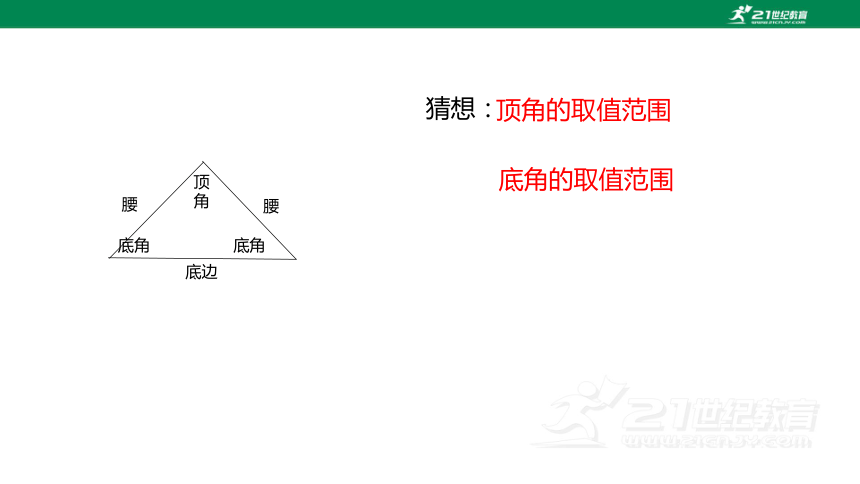
猜想:
顶角的取值范围
底角的取值范围
顶角
底角
底角
腰
腰
底边
顶角
底角
底角
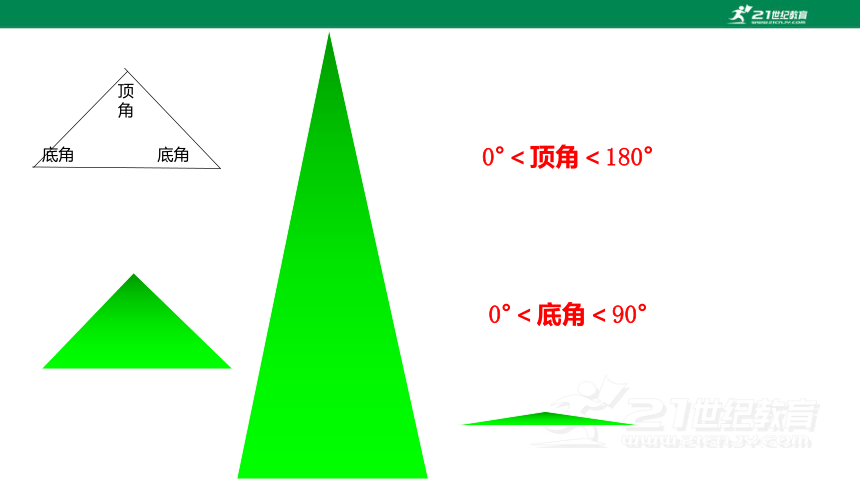
0°<顶角<180°
0°<底角<90°
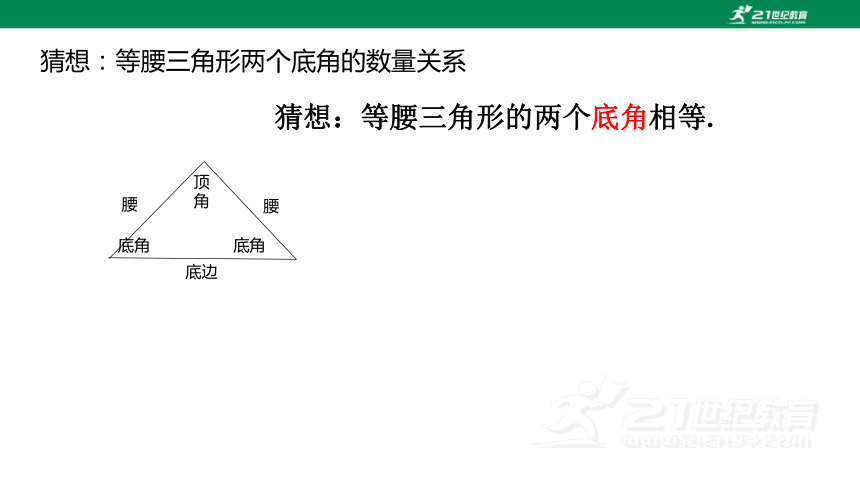
猜想:等腰三角形两个底角的数量关系
顶角
底角
底角
腰
腰
底边
猜想:等腰三角形的两个底角相等.
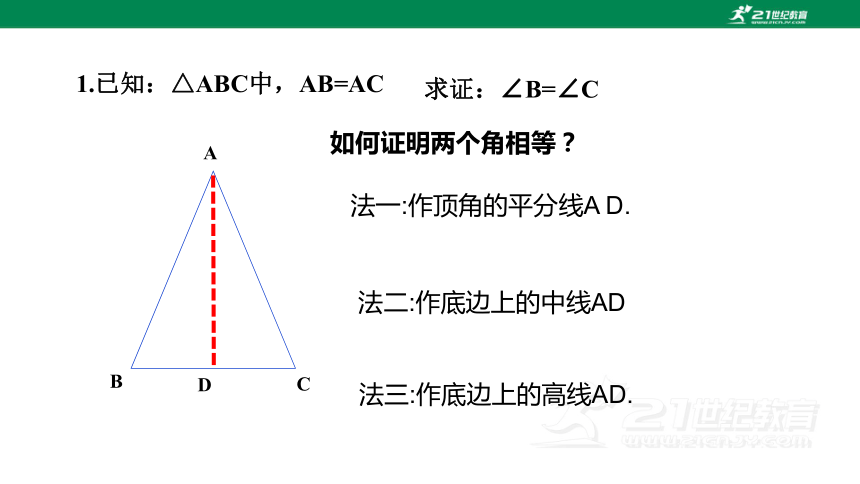
1.已知:△ABC中,AB=AC
求证:∠B=∠C
A
B
C
D
法一:作顶角的平分线A D.
法二:作底边上的中线AD
法三:作底边上的高线AD.
如何证明两个角相等?
A
B
C
D
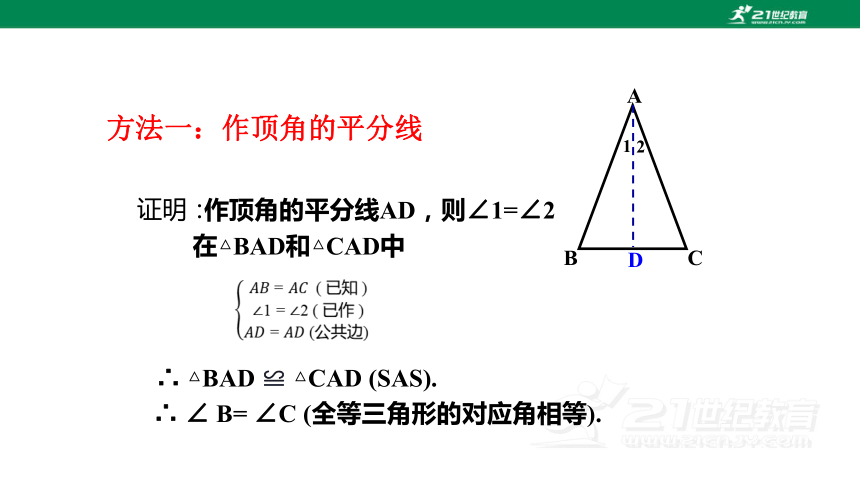
证明:
作顶角的平分线AD,则∠1=∠2
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
方法一:作顶角的平分线
在△BAD和△CAD中
1
2
.
A
B
C
D
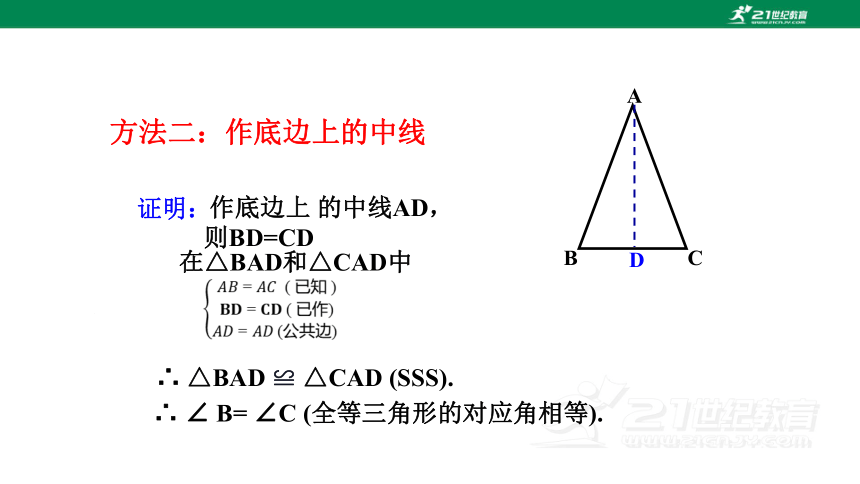
作底边上 的中线AD,
则BD=CD
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法二:作底边上的中线
证明:
。
A
C
B
A
C
B
A
C
B
┐
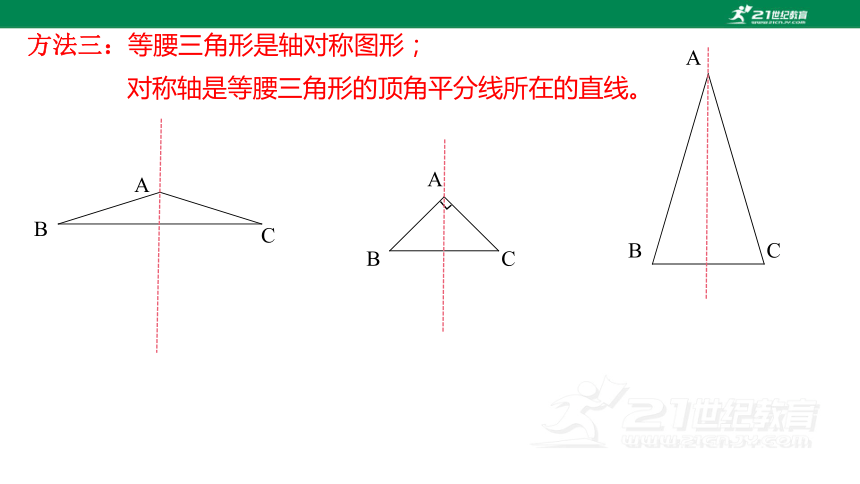
方法三:等腰三角形是轴对称图形;
对称轴是等腰三角形的顶角平分线所在的直线。
自编三道:已知等腰三角形某一个角的度数,求另外两个角的度数
学以致用:
顶角+2×底角=180°
顶角
底角
底角
腰
腰
底边
2. 底角=(180°-顶角)÷2
1. 顶角=180°-2×底角
解:
∵ AB=AC
∴ ∠ B= ∠C(等腰三角形的两个底角相等)
∵ ∠A+∠B+∠C=180°,
∠A=50°
∴ ∠B=∠C= (180°- ∠A)= (180°- 50°)=65°
2.已知:等腰三角形的一个底角为 50 °, 求另两个角的度数.
1. 50 °为顶角:另两个角的度数为65°,65°
另两个角的度数为50°,80°
1.如图,在△ABC中AB=AC,∠A=50°,求∠ B,∠C的度数。
50°
A
B
C
2. 50 °为底角:另两个角的度数为50°,80°
3.已知:等腰三角形的一个角为 50 °, 求另两个角的度数.
指代不明,分类讨论
2.求等边三角形ABC三个内角的度数.
A
B
C
解 如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等腰三角形的两个底角相等).
同理,∠A=∠B.
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=180°÷3=60°.
3. 如图,AD,BE是等边三角形ABC的两条角平分线,AD、BE相交于点O. 求∠AOB的度数.
解:∵△ABC是等边三角形
∴ ∠BAC=∠ABC=60°
∵ AD,BE是等边三角形ABC的角平分线
∴ ∠BAO=∠DAC=30°
∠ABO=∠EBC=30°
∴ ∠AOB=180°-∠BAO - ∠ABO=120°
4. 猜想:与等腰三角形两底角相关的性质.
顶角
底角
底角
腰
腰
底边
等腰三角形两底角的平分线相等.
求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.
求证:BD=CE
证明:∵ AB=AC(已知)
∴ ∠CBD= ∠ABC, ∠BCE= ∠ACB
∴ △BCE≌△CBD(ASA)
∴ ∠ABC=∠ACB(等腰三角形的两个底角相等)
∵ BD,CE分别是∠ABC和∠ACB的平分线
∴ ∠CBD=∠BCE
在△BCE和△CBD中
∴ BD=CE(全等三角形的对应边相等)
法1:
已知:如图,在△ABC中,AB=AC,BD和CE是△ABC的两 条角平分线. 求证:BD=CE
证明:∵ AB=AC(已知)
∴ ∠ABD= ∠ABC, ∠ACE= ∠ACB(角平分线的定义)
∴ BD=CE(全等三角形的对应边相等)
∴ ∠ABC=∠ACB(等腰三角形的两个底角相等)
∵ BD,CE分别是∠ABC和∠ACB的平分线
∴ ∠ABD=∠ACE
△ABD和△ACE中
∴ △ABD≌△ACE(ASA)
法2:
1.等腰三角形的性质定理1
定理:等腰三角形的两个底角相等,
也就是说,在同一个三角形中,等边对等角.
2.等边三角形的性质
定理:等边三角形的各个内角都等于600.
等边三角形的特殊性质主要指:
三个内角都相等,三条边都相等,是轴对称图形且有三条对称轴.
归纳总结:
1 填空:在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为_____。
(2)已知底角为70°,其余两个角分别为_____ 。
(3)已知一个角为70°, 其余两个角分别为______
(4)已知一个角为100°,其余两个角分别为_____ 。
55°, 55°
70°, 40°
55°, 55°或70°, 40°
40°, 40°
当堂检测:
0°<顶角<180°
0°<底角<90°
2.如图,△ABC中,已知,AB=AC,点D在CA的延长线上,∠DAB=50°,则∠B的度数为( )
A.25° B.30° C.40° D.45°
A
等腰三角形顶角的外角是底角的2倍
3.证明:在一个三角形中,较大的边所对的角也较大.
也可以说成:在同一个三角形中,大边对大角.
已知:如图,在△ABC中,AB>AC,求证:∠ACB>∠ABC
A
B
C
D
证明:∵AB>AC,在AB上截取AD,使AD=AC,连接CD
∴∠ADC=∠ACD (在同一个三角形中,等边对等角)
∵∠ADC >∠ABC (三角形的外角大于与它不相邻的内角)
∠ACB>∠ACD (几何直观)
∴∠ACB>∠ADC >∠ABC
截取----构造等腰三角形
连续递推,豁然开朗
A
C
B
D
1
2
3
解:∵BD=AD, ∴ ∠1= ∠A
∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A
∵ BD=BC, ∴ ∠3= ∠C, ∴ ∠C=2 ∠A
∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A
∵ ∠A+ ∠ABC+ ∠C=1800, ∴ 5 ∠A=1800,
∴ ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720
4.如图:在三角形ABC中,AB=AC , D在 AC上,且BD=BC=AD,
求△ABC各内角的度数?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
2.3 等腰三角形的性质(1)
浙教版八年级上册
有两条边相等的三角形叫做等腰三角形.
(1)相等的两边都叫做腰,
另一边叫做底边,
(2)两腰的夹角叫做顶角,
(3)腰和底边的夹角叫做底角.
腰
腰
底边
顶角
底角
底角
A
B
C
温故知新:
猜想:
顶角的取值范围
底角的取值范围
顶角
底角
底角
腰
腰
底边
顶角
底角
底角
0°<顶角<180°
0°<底角<90°
猜想:等腰三角形两个底角的数量关系
顶角
底角
底角
腰
腰
底边
猜想:等腰三角形的两个底角相等.
1.已知:△ABC中,AB=AC
求证:∠B=∠C
A
B
C
D
法一:作顶角的平分线A D.
法二:作底边上的中线AD
法三:作底边上的高线AD.
如何证明两个角相等?
A
B
C
D
证明:
作顶角的平分线AD,则∠1=∠2
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
方法一:作顶角的平分线
在△BAD和△CAD中
1
2
.
A
B
C
D
作底边上 的中线AD,
则BD=CD
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法二:作底边上的中线
证明:
。
A
C
B
A
C
B
A
C
B
┐
方法三:等腰三角形是轴对称图形;
对称轴是等腰三角形的顶角平分线所在的直线。
自编三道:已知等腰三角形某一个角的度数,求另外两个角的度数
学以致用:
顶角+2×底角=180°
顶角
底角
底角
腰
腰
底边
2. 底角=(180°-顶角)÷2
1. 顶角=180°-2×底角
解:
∵ AB=AC
∴ ∠ B= ∠C(等腰三角形的两个底角相等)
∵ ∠A+∠B+∠C=180°,
∠A=50°
∴ ∠B=∠C= (180°- ∠A)= (180°- 50°)=65°
2.已知:等腰三角形的一个底角为 50 °, 求另两个角的度数.
1. 50 °为顶角:另两个角的度数为65°,65°
另两个角的度数为50°,80°
1.如图,在△ABC中AB=AC,∠A=50°,求∠ B,∠C的度数。
50°
A
B
C
2. 50 °为底角:另两个角的度数为50°,80°
3.已知:等腰三角形的一个角为 50 °, 求另两个角的度数.
指代不明,分类讨论
2.求等边三角形ABC三个内角的度数.
A
B
C
解 如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等腰三角形的两个底角相等).
同理,∠A=∠B.
∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=180°÷3=60°.
3. 如图,AD,BE是等边三角形ABC的两条角平分线,AD、BE相交于点O. 求∠AOB的度数.
解:∵△ABC是等边三角形
∴ ∠BAC=∠ABC=60°
∵ AD,BE是等边三角形ABC的角平分线
∴ ∠BAO=∠DAC=30°
∠ABO=∠EBC=30°
∴ ∠AOB=180°-∠BAO - ∠ABO=120°
4. 猜想:与等腰三角形两底角相关的性质.
顶角
底角
底角
腰
腰
底边
等腰三角形两底角的平分线相等.
求证:等腰三角形两底角的平分线相等.
已知:如图,在△ABC中,AB=AC,BD和CE是△ABC的两条角平分线.
求证:BD=CE
证明:∵ AB=AC(已知)
∴ ∠CBD= ∠ABC, ∠BCE= ∠ACB
∴ △BCE≌△CBD(ASA)
∴ ∠ABC=∠ACB(等腰三角形的两个底角相等)
∵ BD,CE分别是∠ABC和∠ACB的平分线
∴ ∠CBD=∠BCE
在△BCE和△CBD中
∴ BD=CE(全等三角形的对应边相等)
法1:
已知:如图,在△ABC中,AB=AC,BD和CE是△ABC的两 条角平分线. 求证:BD=CE
证明:∵ AB=AC(已知)
∴ ∠ABD= ∠ABC, ∠ACE= ∠ACB(角平分线的定义)
∴ BD=CE(全等三角形的对应边相等)
∴ ∠ABC=∠ACB(等腰三角形的两个底角相等)
∵ BD,CE分别是∠ABC和∠ACB的平分线
∴ ∠ABD=∠ACE
△ABD和△ACE中
∴ △ABD≌△ACE(ASA)
法2:
1.等腰三角形的性质定理1
定理:等腰三角形的两个底角相等,
也就是说,在同一个三角形中,等边对等角.
2.等边三角形的性质
定理:等边三角形的各个内角都等于600.
等边三角形的特殊性质主要指:
三个内角都相等,三条边都相等,是轴对称图形且有三条对称轴.
归纳总结:
1 填空:在等腰三角形中,
(1)已知顶角为70°,其余两个角分别为_____。
(2)已知底角为70°,其余两个角分别为_____ 。
(3)已知一个角为70°, 其余两个角分别为______
(4)已知一个角为100°,其余两个角分别为_____ 。
55°, 55°
70°, 40°
55°, 55°或70°, 40°
40°, 40°
当堂检测:
0°<顶角<180°
0°<底角<90°
2.如图,△ABC中,已知,AB=AC,点D在CA的延长线上,∠DAB=50°,则∠B的度数为( )
A.25° B.30° C.40° D.45°
A
等腰三角形顶角的外角是底角的2倍
3.证明:在一个三角形中,较大的边所对的角也较大.
也可以说成:在同一个三角形中,大边对大角.
已知:如图,在△ABC中,AB>AC,求证:∠ACB>∠ABC
A
B
C
D
证明:∵AB>AC,在AB上截取AD,使AD=AC,连接CD
∴∠ADC=∠ACD (在同一个三角形中,等边对等角)
∵∠ADC >∠ABC (三角形的外角大于与它不相邻的内角)
∠ACB>∠ACD (几何直观)
∴∠ACB>∠ADC >∠ABC
截取----构造等腰三角形
连续递推,豁然开朗
A
C
B
D
1
2
3
解:∵BD=AD, ∴ ∠1= ∠A
∵ ∠3= ∠1+ ∠A, ∴ ∠3=2 ∠A
∵ BD=BC, ∴ ∠3= ∠C, ∴ ∠C=2 ∠A
∵ AB=AC, ∴ ∠ABC= ∠C=2 ∠A
∵ ∠A+ ∠ABC+ ∠C=1800, ∴ 5 ∠A=1800,
∴ ∠A=360, ∴ ∠ABC= ∠C=2 ∠A=720
4.如图:在三角形ABC中,AB=AC , D在 AC上,且BD=BC=AD,
求△ABC各内角的度数?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
