第1-2章练习(含答案)浙教版数学八年级上册
文档属性
| 名称 | 第1-2章练习(含答案)浙教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 403.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 11:11:39 | ||
图片预览

文档简介
第一-二章练习
一、选择题
1.对称性不仅是数学的美学体现,更是生物适应环境的“最优解”。下列生物的外轮廓同时
具备轴对称性和中心对称性的是( )
A. B.
C. D.
2.以下列每组数为长度(单位:cm)的三根小木棒,其中能搭成三角形的是( )
A.1, 2. 3 B.2,2, 4 C.3,4.5 D.3,4,8
3.如图,若两个三角形全等,图中字母表示三角形边长,则的度数为( )
A. B. C. D.
4.如图,小谊将两根长度不等的木条AC,BD的中点连在一起,记中点为O,即AO=CO,BO=DO.测得C,D两点之间的距离后,利用全等三角形的性质,可得花瓶内壁上A,B两点之间的距离.图中△AOB与△COD全等的依据是( )
A.SSS B.SAS C.ASA D.HL
5.下列命题是假命题的是( )
A.“对顶角相等”的逆命题是假命题
B.在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a∥c
C.两条平行线被第三条直线所截,内错角相等
D.同旁内角互补两直线平行
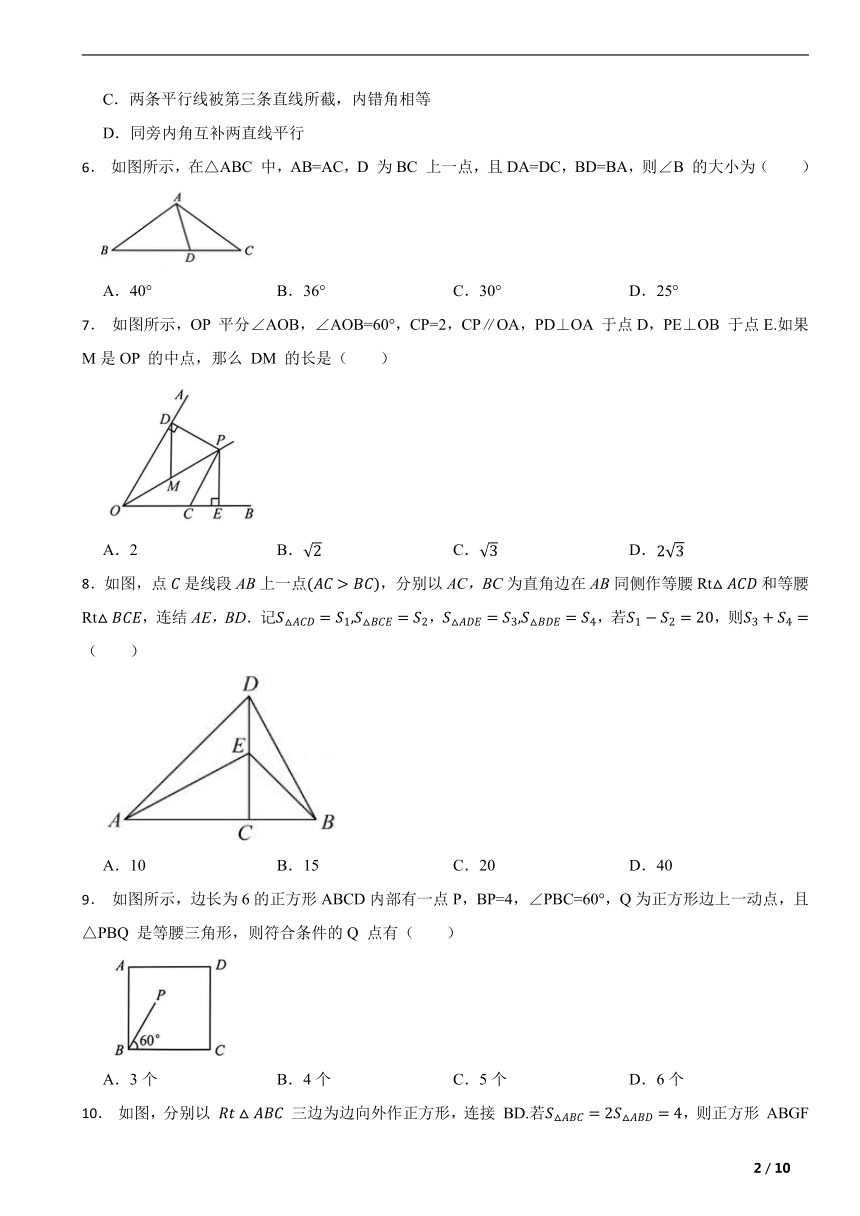
6. 如图所示,在△ABC 中,AB=AC,D 为BC 上一点,且DA=DC,BD=BA,则∠B 的大小为( )
A.40° B.36° C.30° D.25°
7. 如图所示,OP 平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA 于点D,PE⊥OB 于点E.如果M是OP 的中点,那么 DM 的长是( )
A.2 B. C. D.
8.如图,点是线段AB上一点,分别以AC,BC为直角边在AB同侧作等腰Rt和等腰Rt,连结AE,BD.记,,若,则( )
A.10 B.15 C.20 D.40
9. 如图所示,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,Q为正方形边上一动点,且△PBQ 是等腰三角形,则符合条件的Q 点有( )
A.3个 B.4个 C.5个 D.6个
10. 如图,分别以 三边为边向外作正方形,连接 BD.若,则正方形 ABGF 的面积为( )
A.8 B.10 C.16 D.20
二、填空题
11.能说明“若,则”是假命题的一个反例可以是 .
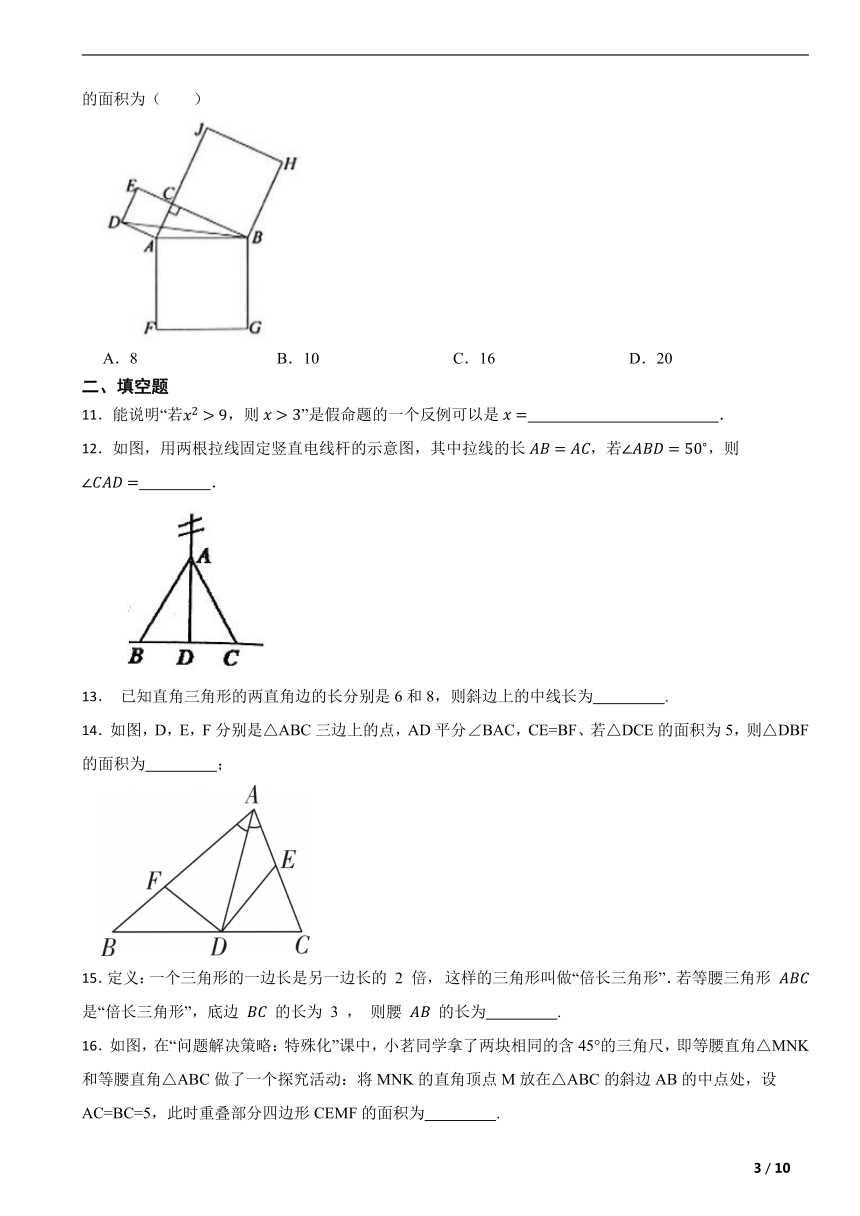
12.如图,用两根拉线固定竖直电线杆的示意图,其中拉线的长,若,则 .
13. 已知直角三角形的两直角边的长分别是6和8,则斜边上的中线长为 .
14.如图,D,E,F分别是△ABC三边上的点,AD平分∠BAC,CE=BF、若△DCE的面积为5,则△DBF的面积为 ;
15.定义:一个三角形的一边长是另一边长的 2 倍, 这样的三角形叫做“倍长三角形”.若等腰三角形 是“倍长三角形”,底边 的长为 3 , 则腰 的长为 .
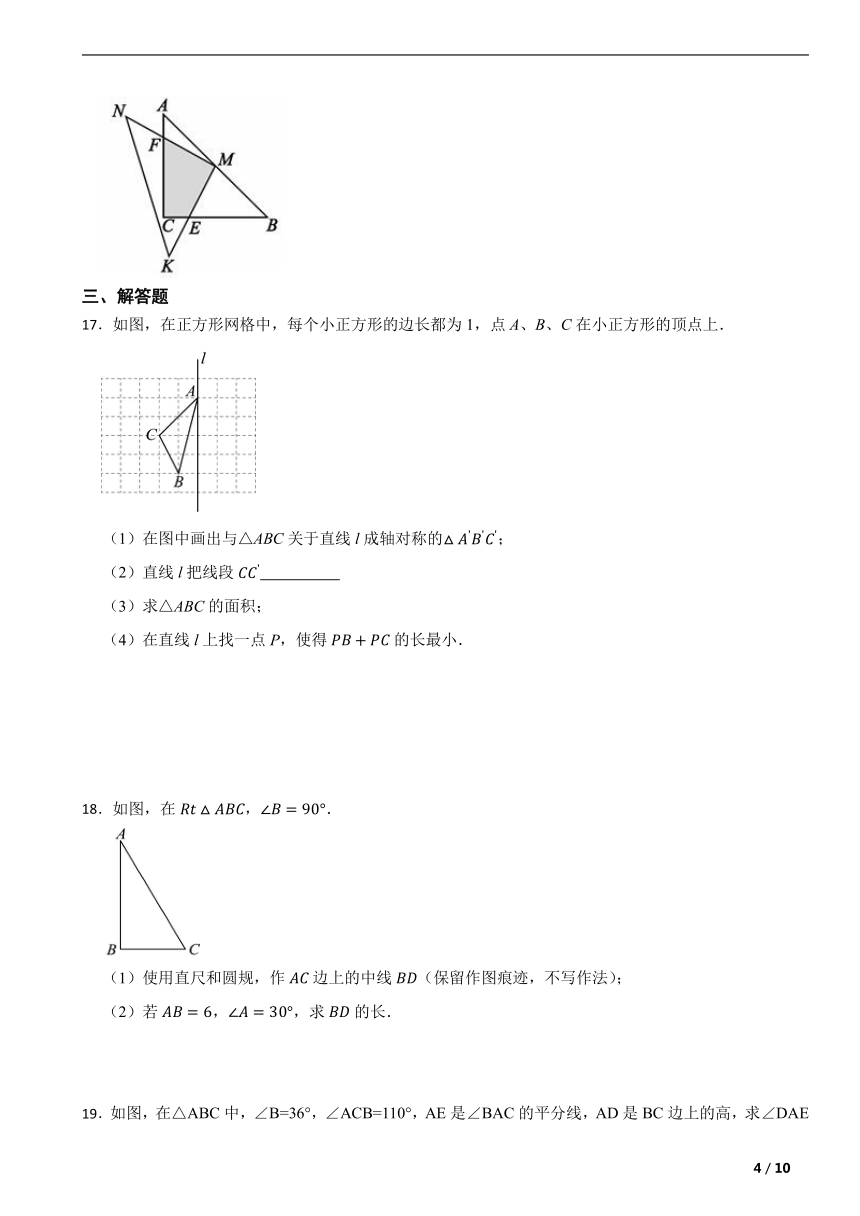
16.如图,在“问题解决策略:特殊化”课中,小茗同学拿了两块相同的含45°的三角尺,即等腰直角△MNK和等腰直角△ABC做了一个探究活动:将MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=5,此时重叠部分四边形CEMF的面积为 .
三、解答题
17.如图,在正方形网格中,每个小正方形的边长都为1,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的;
(2)直线l把线段
(3)求△ABC的面积;
(4)在直线l上找一点P,使得的长最小.
18.如图,在,.
(1)使用直尺和圆规,作边上的中线(保留作图痕迹,不写作法);
(2)若,,求的长.
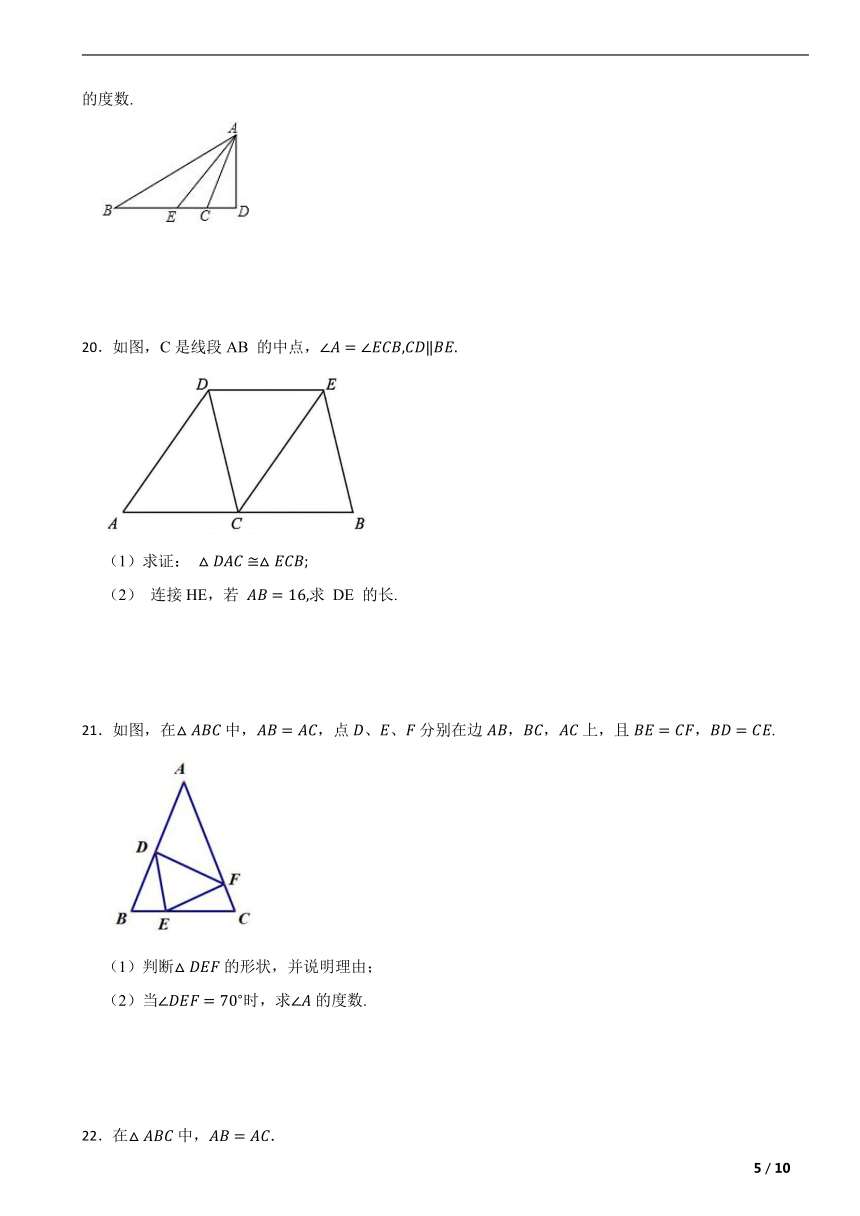
19.如图,在△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线,AD是BC边上的高,求∠DAE的度数.
20.如图,C是线段AB 的中点,
(1)求证:
(2) 连接HE,若 求 DE 的长.
21.如图,在中,,点、、分别在边,,上,且,.
(1)判断的形状,并说明理由;
(2)当时,求的度数.
22.在中,.
(1)如图①,如果,是中边上的高,并且,则 °;
(2)如图②,如果,是中边上的高,并且,则 °;
(3)由(1),(2)猜想:与之间有什么数量关系?请用式子表示: ;
(4)如图③,如果不是中BC边上的高,但仍有,请判断与之间是否仍然存在(3)中的数量关系 请说明理由.
23.某实践探究小组在放风筝时想测量风筝离地面的垂直高度,通过勘测,得到如下记录表:
测量示意图
测量数据 边的长度 ①测得水平距离的长为15米.
②根据手中剩余线的长度计算出了风筝拉线的长为17米.
③小明牵线放风筝的手到地面的距离为1.7米.
数据处理组得到上面数据以后做了认真分析,他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度.请完成以下任务:
(1)根据上述信息,求风筝离地面的垂直高度.
(2)如果小明想要风筝沿方向再上升12米,BC长度不变,则他应该再放出多少米风筝拉线?
参考答案
1.D
2.C
3.A
4.B
5.B
6.B
7.C
8.C
9.C
10.D
11.(答案不唯一)
12.
13.5
14.5
15.6
16.
17.(1)解:如图,即为所求.
.
(2)解:∵与为轴对称图形,∴直线l把线段垂直平分,故答案为:垂直平分.
(3)解:的面积为:
(4)解:如图,点P即为所求.
18.(1)解:分别以点、为圆心,大于一半长为半径画弧,两条弧分别相交于点和,连接交于点,连接,即为所求作的边上的中线.
(2)解:,,
.
在,,
,
,
.
是中边上的中线,
.
19.解:由三角形内角和定理,得∠BAC=180°-∠B-∠ACB=34°;
由AE是∠BAC的平分线,得∠BAE=∠BAC=17°;
∠AED是△ABE的外角,得∠DEA=∠B+∠BAE=53°;
由AD是BC边上的高可知,△AED为直角三角形,所以得∠DAE=90°-∠AED=37°.
20.(1)证明:∵是线段的中点,
∴,
∵,
∴,
在和中,
,
∴;
(2)解:∵,是线段的中点,
∴,
由(1)得,
∴,
又∵,
∴四边形是平行四边形,
∴.
21.(1)解:是等腰三角形,理由如下:
在和中:
是等腰三角形;
(2)解:
∴
在中,,
∴,
.
22.(1)15
(2)20
(3)
(4)解:仍然成立.理由如下:
∵,
∴.
∵,.
∴.
∴.
∵,
∴.
∴,
∴.
23.(1)解:∵在中,,,
,
又米,米,
米,
答:线段的长为9.7米;
(2)解:∵风筝沿方向再上升12米后,米,
∴此时风筝线的长为:(米),
∴风筝应该放出线的长度为:米,
答:他应该再放出8米线.
1 / 1
一、选择题
1.对称性不仅是数学的美学体现,更是生物适应环境的“最优解”。下列生物的外轮廓同时
具备轴对称性和中心对称性的是( )
A. B.
C. D.
2.以下列每组数为长度(单位:cm)的三根小木棒,其中能搭成三角形的是( )
A.1, 2. 3 B.2,2, 4 C.3,4.5 D.3,4,8
3.如图,若两个三角形全等,图中字母表示三角形边长,则的度数为( )
A. B. C. D.
4.如图,小谊将两根长度不等的木条AC,BD的中点连在一起,记中点为O,即AO=CO,BO=DO.测得C,D两点之间的距离后,利用全等三角形的性质,可得花瓶内壁上A,B两点之间的距离.图中△AOB与△COD全等的依据是( )
A.SSS B.SAS C.ASA D.HL
5.下列命题是假命题的是( )
A.“对顶角相等”的逆命题是假命题
B.在同一平面内,a、b、c是直线,且a∥b,b⊥c,则a∥c
C.两条平行线被第三条直线所截,内错角相等
D.同旁内角互补两直线平行
6. 如图所示,在△ABC 中,AB=AC,D 为BC 上一点,且DA=DC,BD=BA,则∠B 的大小为( )
A.40° B.36° C.30° D.25°
7. 如图所示,OP 平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA 于点D,PE⊥OB 于点E.如果M是OP 的中点,那么 DM 的长是( )
A.2 B. C. D.
8.如图,点是线段AB上一点,分别以AC,BC为直角边在AB同侧作等腰Rt和等腰Rt,连结AE,BD.记,,若,则( )
A.10 B.15 C.20 D.40
9. 如图所示,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,Q为正方形边上一动点,且△PBQ 是等腰三角形,则符合条件的Q 点有( )
A.3个 B.4个 C.5个 D.6个
10. 如图,分别以 三边为边向外作正方形,连接 BD.若,则正方形 ABGF 的面积为( )
A.8 B.10 C.16 D.20
二、填空题
11.能说明“若,则”是假命题的一个反例可以是 .
12.如图,用两根拉线固定竖直电线杆的示意图,其中拉线的长,若,则 .
13. 已知直角三角形的两直角边的长分别是6和8,则斜边上的中线长为 .
14.如图,D,E,F分别是△ABC三边上的点,AD平分∠BAC,CE=BF、若△DCE的面积为5,则△DBF的面积为 ;
15.定义:一个三角形的一边长是另一边长的 2 倍, 这样的三角形叫做“倍长三角形”.若等腰三角形 是“倍长三角形”,底边 的长为 3 , 则腰 的长为 .
16.如图,在“问题解决策略:特殊化”课中,小茗同学拿了两块相同的含45°的三角尺,即等腰直角△MNK和等腰直角△ABC做了一个探究活动:将MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=5,此时重叠部分四边形CEMF的面积为 .
三、解答题
17.如图,在正方形网格中,每个小正方形的边长都为1,点A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l成轴对称的;
(2)直线l把线段
(3)求△ABC的面积;
(4)在直线l上找一点P,使得的长最小.
18.如图,在,.
(1)使用直尺和圆规,作边上的中线(保留作图痕迹,不写作法);
(2)若,,求的长.
19.如图,在△ABC中,∠B=36°,∠ACB=110°,AE是∠BAC的平分线,AD是BC边上的高,求∠DAE的度数.
20.如图,C是线段AB 的中点,
(1)求证:
(2) 连接HE,若 求 DE 的长.
21.如图,在中,,点、、分别在边,,上,且,.
(1)判断的形状,并说明理由;
(2)当时,求的度数.
22.在中,.
(1)如图①,如果,是中边上的高,并且,则 °;
(2)如图②,如果,是中边上的高,并且,则 °;
(3)由(1),(2)猜想:与之间有什么数量关系?请用式子表示: ;
(4)如图③,如果不是中BC边上的高,但仍有,请判断与之间是否仍然存在(3)中的数量关系 请说明理由.
23.某实践探究小组在放风筝时想测量风筝离地面的垂直高度,通过勘测,得到如下记录表:
测量示意图
测量数据 边的长度 ①测得水平距离的长为15米.
②根据手中剩余线的长度计算出了风筝拉线的长为17米.
③小明牵线放风筝的手到地面的距离为1.7米.
数据处理组得到上面数据以后做了认真分析,他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度.请完成以下任务:
(1)根据上述信息,求风筝离地面的垂直高度.
(2)如果小明想要风筝沿方向再上升12米,BC长度不变,则他应该再放出多少米风筝拉线?
参考答案
1.D
2.C
3.A
4.B
5.B
6.B
7.C
8.C
9.C
10.D
11.(答案不唯一)
12.
13.5
14.5
15.6
16.
17.(1)解:如图,即为所求.
.
(2)解:∵与为轴对称图形,∴直线l把线段垂直平分,故答案为:垂直平分.
(3)解:的面积为:
(4)解:如图,点P即为所求.
18.(1)解:分别以点、为圆心,大于一半长为半径画弧,两条弧分别相交于点和,连接交于点,连接,即为所求作的边上的中线.
(2)解:,,
.
在,,
,
,
.
是中边上的中线,
.
19.解:由三角形内角和定理,得∠BAC=180°-∠B-∠ACB=34°;
由AE是∠BAC的平分线,得∠BAE=∠BAC=17°;
∠AED是△ABE的外角,得∠DEA=∠B+∠BAE=53°;
由AD是BC边上的高可知,△AED为直角三角形,所以得∠DAE=90°-∠AED=37°.
20.(1)证明:∵是线段的中点,
∴,
∵,
∴,
在和中,
,
∴;
(2)解:∵,是线段的中点,
∴,
由(1)得,
∴,
又∵,
∴四边形是平行四边形,
∴.
21.(1)解:是等腰三角形,理由如下:
在和中:
是等腰三角形;
(2)解:
∴
在中,,
∴,
.
22.(1)15
(2)20
(3)
(4)解:仍然成立.理由如下:
∵,
∴.
∵,.
∴.
∴.
∵,
∴.
∴,
∴.
23.(1)解:∵在中,,,
,
又米,米,
米,
答:线段的长为9.7米;
(2)解:∵风筝沿方向再上升12米后,米,
∴此时风筝线的长为:(米),
∴风筝应该放出线的长度为:米,
答:他应该再放出8米线.
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
