初中数学浙教版八年级上册 第三章 一元一次不等式 练习(含答案)
文档属性
| 名称 | 初中数学浙教版八年级上册 第三章 一元一次不等式 练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 144.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 09:42:10 | ||
图片预览




文档简介
第三章 一元一次不等式 练习
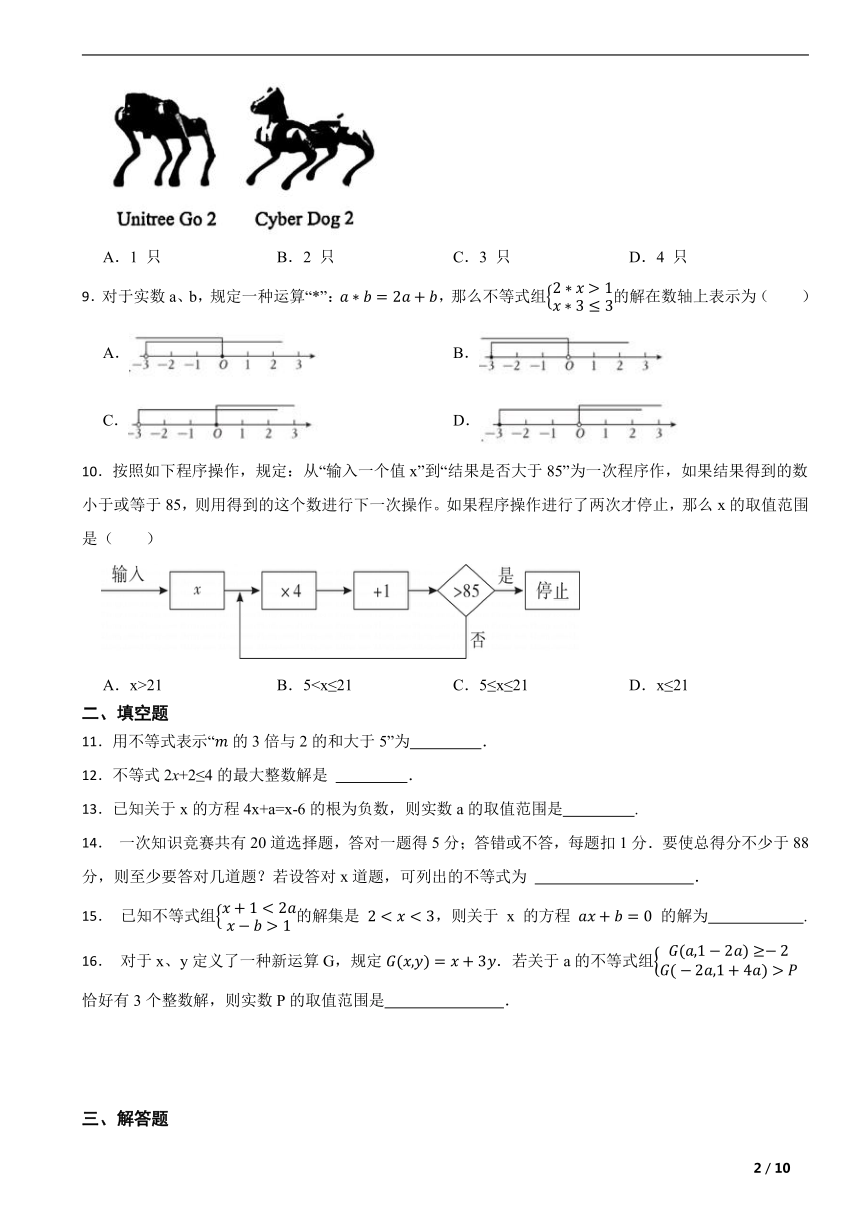
一、选择题
1.下列各式是不等式的是( )
A. B. C. D.
2.下列x的值是不等式x-1>0的解的是( )
A.x=2 B.x=1 C.x=0 D.x=-1
3.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
4.已知,则下列不等式成立的是( )
A. B.
C. D.
5.P,Q,R,S四个小朋友玩跷跷板,结果如图所示,则他们的体重大小关系为( )
A.R6. 如果关于 x 的不等式组 的解集是 , 则 a 的取值范围是 ( )
A. B. C. D.
7.若方程组的解x,y满足0<x+y<1,则k的取值范围是( )
A.﹣4<k<0 B.﹣1<k<0 C.0<k<8 D.k>﹣4
8. 某企业要购进两款机器狗共5只.如图所示,已知 Cyber Dog 2 单价是 1.3 万元/只,Unitree Go 2 单价是 1 万元/只,且该企业购进两款机器狗的总费用不超过 6.2 万元,则 Cyber Dog 2 最多可以购进( )
A.1 只 B.2 只 C.3 只 D.4 只
9.对于实数a、b,规定一种运算“*”:,那么不等式组的解在数轴上表示为( )
A. B.
C. D.
10.按照如下程序操作,规定:从“输入一个值x”到“结果是否大于85”为一次程序作,如果结果得到的数小于或等于85,则用得到的这个数进行下一次操作。如果程序操作进行了两次才停止,那么x的取值范围是( )
A.x>21 B.5二、填空题
11.用不等式表示“的3倍与2的和大于5”为 .
12.不等式2x+2≤4的最大整数解是 .
13.已知关于x的方程4x+a=x-6的根为负数,则实数a的取值范围是 .
14. 一次知识竞赛共有20道选择题,答对一题得5分;答错或不答,每题扣1分.要使总得分不少于88分,则至少要答对几道题?若设答对x道题,可列出的不等式为 .
15. 已知不等式组的解集是 ,则关于 x 的方程 的解为 .
16. 对于x、y定义了一种新运算G,规定.若关于a的不等式组恰好有3个整数解,则实数P的取值范围是 .
三、解答题
17.解不等式组:并把它的解集在数轴上表示出来。
18.下面是小明解不等式,的过程,请认真阅读并完成相应的任务.
解:不等式①,去分母,得, (第一步)
移项,合并同类项,得, (第二步)
系数化为1,得, (第三步)
解不等式②,得, (第四步)|
所以原不等式组无解. (第五步)
根据以上材料,解答下列问题:
(1) 第一步去分母的依据是 .
(2) 在解答过程中,从第 步开始出错,错误原因是
(3) 解不等式组:
19.如图,数轴上点O为原点,点A,B,C表示的数分别是.
(1)______(用含m的代数式表示);
(2)求当与的差不小时,m的最小整数值.
20.已知方程组的解x为非正数,y为负数.
(1)求a的取值范围;
(2)在a的取值范围中,求当a为何整数时,不等式的解为?
21.某小区在小区内安装垃圾分类的A型固定垃圾箱和B型移动垃圾箱,已知购买3个A型固定垃圾箱和2个B型移动垃圾箱共需560元,1个A型固定垃圾箱和1个B型移动垃圾箱共需200元.
(1)求A型固定垃圾箱和B型移动垃圾箱的单价各是多少元;
(2)如果需要购买A型固定垃圾箱和B型移动垃圾箱共90个,且费用不超过6000元,问:那该小区最多可以购买A型固定垃圾箱多少个?
22.阅读材料:
解分式不等式
分析与解 根据实数的除法法则:同号两数相除得正数,异号两数相
除得负数,因此,原不等式可转化为: 或②解不等式组①得无解,解不等式组②得-2请仿照上述方法解下面的分式不等式:
(1)
(2)
23.新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:方程的解为,而不等式组的解集为,不难发现在的范围内,所以方程是不等式组的“关联方程”
(1)在方程①;②;③中,不等式组的“关联方程”是___________(填序号)
(2)关于的方程是不等式组的“关联方程”,求的取值范围;
(3)若关于的方程是关于的不等式组的“关联方程”,且此时不等式组有3个整数解,试求的取值范围.
参考答案
1.A
2.A
3.A
4.C
5.B
6.C
7.A
8.D
9.A
10.B
11.
12.1
13.a>-6
14.5x-(20-x)≥88
15.
16.-17≤p<-7
17.解:
解不等式①可得,x<2
解不等式②可得x≥-4
即不等式组的解集为-4≤x<2
解集在数轴上表示出来如图所示
18.(1)不等式的两边同时乘以(或除以)同一个正数,不等号方向不变
(2)三;原因:①违背了不等式基本性质3:或②不等式的两边同时乘以(或除以)同一个负数,不等号方向未改变:或③不等式的两边同时乘以(或除以)同一个负数,不等号方向应该改变.
(3)解: 由①得,
由②得,
∴ 原不等式组的解集是,
19.(1)2m-1
(2)解:根据题意,可得
BC=(2-m)-(9-4m)
=2-m-9+4m
=3m-7
因为BC与AB的差不小于
所以,3m-7-(2m-1)≥
3m-7-2m+1≥
m-6≥
解得,m≥
所以,m的最小整数值为7
20.(1)解:解方程组得,
由于x为非正数,y为负数,
可列不等式组,
解得-2(2)解:将不等式合并同类项得(2a+1)x>2a+1,
∵不等式的解为,
∴2a+1<0,
∴a<.
又∵-2∴-2∴整数a的值为-1,
故当a为-1时,不等式的解为.
21.(1)解:设A型固定垃圾箱的单价是元,B型移动垃圾箱的单价是元,
根据题意,得,
解得,
答:A型固定垃圾箱的单价是160元,B型移动垃圾箱的单价是40元.
(2)解:设购买A型固定垃圾箱个,则购买B型移动垃圾箱个.
根据题意,得,
解得.
的最大值为20.
答:该小区最多可以购买A型固定垃圾箱20个.
22.(1)解:原不等式可以转化为:
解不等式①得
x≤4
解不等式②得
x≥
∴-2.5<x≤4
解不等式①得
x≥4
解不等式②得
x≤
此不等式无解
∴ 的解集为:-2.5<x≤4
(2)解:原不等式可以转化为:
解不等式①得
x>-2,
解不等式②得
x<3,
∴-2<x<3,
解不等式①得
x<-2,
解不等式②得
x>3,
此不等式无解
∴ 的解集为:-2<x<3
23.(1)①③
(2)解:,
解不等式①得,,
解不等式②得,,
∴不等式组的解集为,
解得:,
∵关于的方程是不等式组的“关联方程”,
∴,
∴,
∴;
(3)解:,
解不等式①得,,
解不等式②得,,
∴不等式组的解集为,
解得:;
∵关于的方程是关于的不等式组的“关联方程”,
∴,
解得,
又∵不等式组有3个整数解,
∴,
解得,
∴m的取值范围为:.
1 / 1
一、选择题
1.下列各式是不等式的是( )
A. B. C. D.
2.下列x的值是不等式x-1>0的解的是( )
A.x=2 B.x=1 C.x=0 D.x=-1
3.不等式的解集在数轴上表示正确的是( )
A. B.
C. D.
4.已知,则下列不等式成立的是( )
A. B.
C. D.
5.P,Q,R,S四个小朋友玩跷跷板,结果如图所示,则他们的体重大小关系为( )
A.R
A. B. C. D.
7.若方程组的解x,y满足0<x+y<1,则k的取值范围是( )
A.﹣4<k<0 B.﹣1<k<0 C.0<k<8 D.k>﹣4
8. 某企业要购进两款机器狗共5只.如图所示,已知 Cyber Dog 2 单价是 1.3 万元/只,Unitree Go 2 单价是 1 万元/只,且该企业购进两款机器狗的总费用不超过 6.2 万元,则 Cyber Dog 2 最多可以购进( )
A.1 只 B.2 只 C.3 只 D.4 只
9.对于实数a、b,规定一种运算“*”:,那么不等式组的解在数轴上表示为( )
A. B.
C. D.
10.按照如下程序操作,规定:从“输入一个值x”到“结果是否大于85”为一次程序作,如果结果得到的数小于或等于85,则用得到的这个数进行下一次操作。如果程序操作进行了两次才停止,那么x的取值范围是( )
A.x>21 B.5
11.用不等式表示“的3倍与2的和大于5”为 .
12.不等式2x+2≤4的最大整数解是 .
13.已知关于x的方程4x+a=x-6的根为负数,则实数a的取值范围是 .
14. 一次知识竞赛共有20道选择题,答对一题得5分;答错或不答,每题扣1分.要使总得分不少于88分,则至少要答对几道题?若设答对x道题,可列出的不等式为 .
15. 已知不等式组的解集是 ,则关于 x 的方程 的解为 .
16. 对于x、y定义了一种新运算G,规定.若关于a的不等式组恰好有3个整数解,则实数P的取值范围是 .
三、解答题
17.解不等式组:并把它的解集在数轴上表示出来。
18.下面是小明解不等式,的过程,请认真阅读并完成相应的任务.
解:不等式①,去分母,得, (第一步)
移项,合并同类项,得, (第二步)
系数化为1,得, (第三步)
解不等式②,得, (第四步)|
所以原不等式组无解. (第五步)
根据以上材料,解答下列问题:
(1) 第一步去分母的依据是 .
(2) 在解答过程中,从第 步开始出错,错误原因是
(3) 解不等式组:
19.如图,数轴上点O为原点,点A,B,C表示的数分别是.
(1)______(用含m的代数式表示);
(2)求当与的差不小时,m的最小整数值.
20.已知方程组的解x为非正数,y为负数.
(1)求a的取值范围;
(2)在a的取值范围中,求当a为何整数时,不等式的解为?
21.某小区在小区内安装垃圾分类的A型固定垃圾箱和B型移动垃圾箱,已知购买3个A型固定垃圾箱和2个B型移动垃圾箱共需560元,1个A型固定垃圾箱和1个B型移动垃圾箱共需200元.
(1)求A型固定垃圾箱和B型移动垃圾箱的单价各是多少元;
(2)如果需要购买A型固定垃圾箱和B型移动垃圾箱共90个,且费用不超过6000元,问:那该小区最多可以购买A型固定垃圾箱多少个?
22.阅读材料:
解分式不等式
分析与解 根据实数的除法法则:同号两数相除得正数,异号两数相
除得负数,因此,原不等式可转化为: 或②解不等式组①得无解,解不等式组②得-2
(1)
(2)
23.新定义:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“关联方程”,例如:方程的解为,而不等式组的解集为,不难发现在的范围内,所以方程是不等式组的“关联方程”
(1)在方程①;②;③中,不等式组的“关联方程”是___________(填序号)
(2)关于的方程是不等式组的“关联方程”,求的取值范围;
(3)若关于的方程是关于的不等式组的“关联方程”,且此时不等式组有3个整数解,试求的取值范围.
参考答案
1.A
2.A
3.A
4.C
5.B
6.C
7.A
8.D
9.A
10.B
11.
12.1
13.a>-6
14.5x-(20-x)≥88
15.
16.-17≤p<-7
17.解:
解不等式①可得,x<2
解不等式②可得x≥-4
即不等式组的解集为-4≤x<2
解集在数轴上表示出来如图所示
18.(1)不等式的两边同时乘以(或除以)同一个正数,不等号方向不变
(2)三;原因:①违背了不等式基本性质3:或②不等式的两边同时乘以(或除以)同一个负数,不等号方向未改变:或③不等式的两边同时乘以(或除以)同一个负数,不等号方向应该改变.
(3)解: 由①得,
由②得,
∴ 原不等式组的解集是,
19.(1)2m-1
(2)解:根据题意,可得
BC=(2-m)-(9-4m)
=2-m-9+4m
=3m-7
因为BC与AB的差不小于
所以,3m-7-(2m-1)≥
3m-7-2m+1≥
m-6≥
解得,m≥
所以,m的最小整数值为7
20.(1)解:解方程组得,
由于x为非正数,y为负数,
可列不等式组,
解得-2
∵不等式的解为,
∴2a+1<0,
∴a<.
又∵-2
故当a为-1时,不等式的解为.
21.(1)解:设A型固定垃圾箱的单价是元,B型移动垃圾箱的单价是元,
根据题意,得,
解得,
答:A型固定垃圾箱的单价是160元,B型移动垃圾箱的单价是40元.
(2)解:设购买A型固定垃圾箱个,则购买B型移动垃圾箱个.
根据题意,得,
解得.
的最大值为20.
答:该小区最多可以购买A型固定垃圾箱20个.
22.(1)解:原不等式可以转化为:
解不等式①得
x≤4
解不等式②得
x≥
∴-2.5<x≤4
解不等式①得
x≥4
解不等式②得
x≤
此不等式无解
∴ 的解集为:-2.5<x≤4
(2)解:原不等式可以转化为:
解不等式①得
x>-2,
解不等式②得
x<3,
∴-2<x<3,
解不等式①得
x<-2,
解不等式②得
x>3,
此不等式无解
∴ 的解集为:-2<x<3
23.(1)①③
(2)解:,
解不等式①得,,
解不等式②得,,
∴不等式组的解集为,
解得:,
∵关于的方程是不等式组的“关联方程”,
∴,
∴,
∴;
(3)解:,
解不等式①得,,
解不等式②得,,
∴不等式组的解集为,
解得:;
∵关于的方程是关于的不等式组的“关联方程”,
∴,
解得,
又∵不等式组有3个整数解,
∴,
解得,
∴m的取值范围为:.
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
