初中数学浙教版八年级上册 第二章 特殊三角形 练习(含答案)
文档属性
| 名称 | 初中数学浙教版八年级上册 第二章 特殊三角形 练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 447.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 09:44:26 | ||
图片预览


文档简介
第二章 特殊三角形 练习
一、选择题
1. 我国新能源汽车产业发展迅猛,取得了举世瞩目的成就,下列新能源汽车标志既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2. 下列各组数据中,可以作为直角三角形三边长的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
3. 下列命题的逆命题正确的是( )
A.全等三角形的面积相等
B.全等三角形的周长相等
C.两个锐角互余的三角形是直角三角形
D.如果,那么
4.如图,在中,,,且,.则长为( )
A.1 B.2 C.3 D.4
5.等腰三角形底边长为,一腰上的中线把这个三角形的周长分为两部分,其差为,则该等腰三角形的腰长为( )
A. B. C. D.或
6.如图,在中,,,,则的长为( )
A.7 B.8 C.10 D.12
7.如图,已知,垂足为点O,,要根据“”证明,还需要添加的一个条件是( )
A. B. C. D.
8.在中,,,斜边上的高,则( )
A. B.6 C. D.9
9. 若三边长分别为,,,则的面积为( )
A.2 B.4 C. D.
10.如图,在等边中,,点,分别在边,上,且,连接,交于点,连接,则的最小值是( )
A.2 B.3 C. D.
二、填空题
11.已知命题“若,则”,其逆命题是 命题(填“真”或“假”).
12.在△ABC中,AB=AC。若∠A=40°,则∠C的大小为 .
13.如图,测量三角形纸片的尺寸,点,分别对应刻度尺上的刻度2和8,为的中点,若,则的长为 .
14. 如图,将两个完全相同的直角三角形纸板叠放在一起,。若,则CE的长度为 。
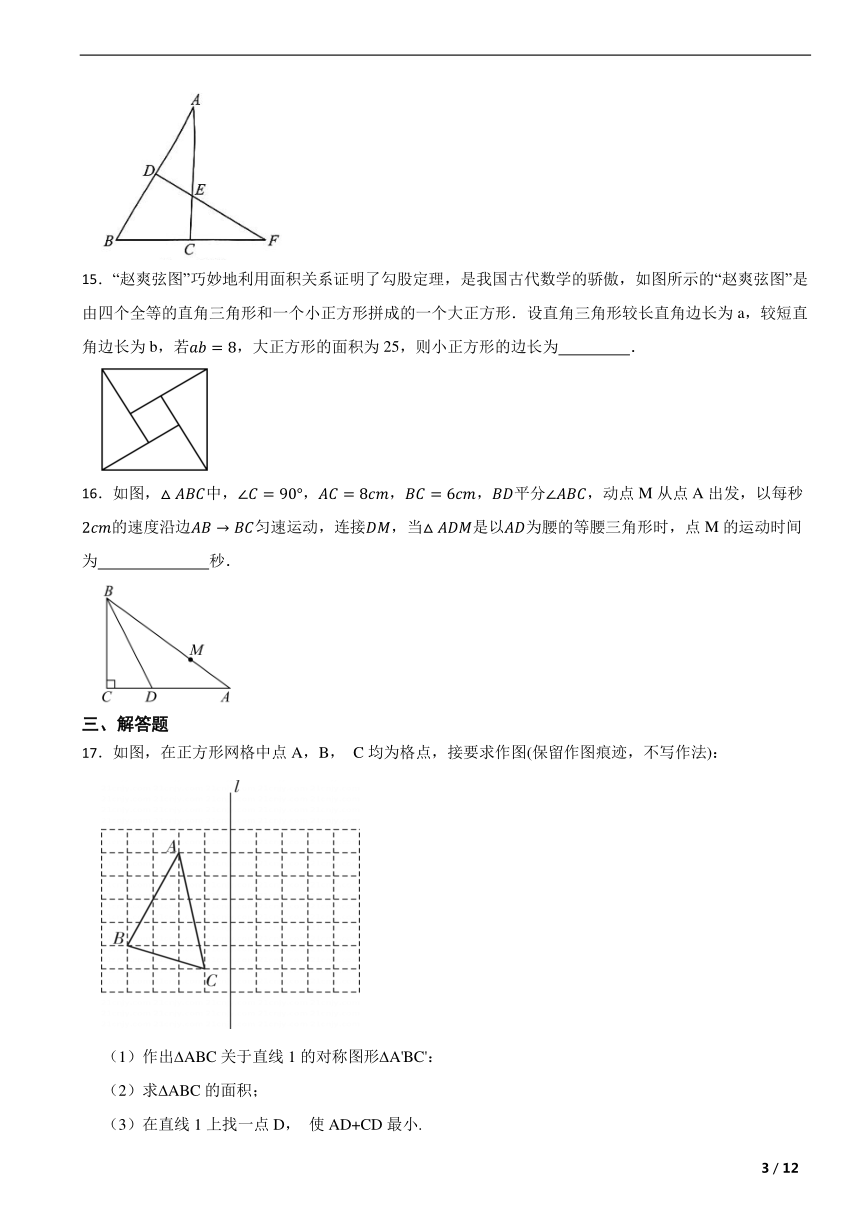
15.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为25,则小正方形的边长为 .
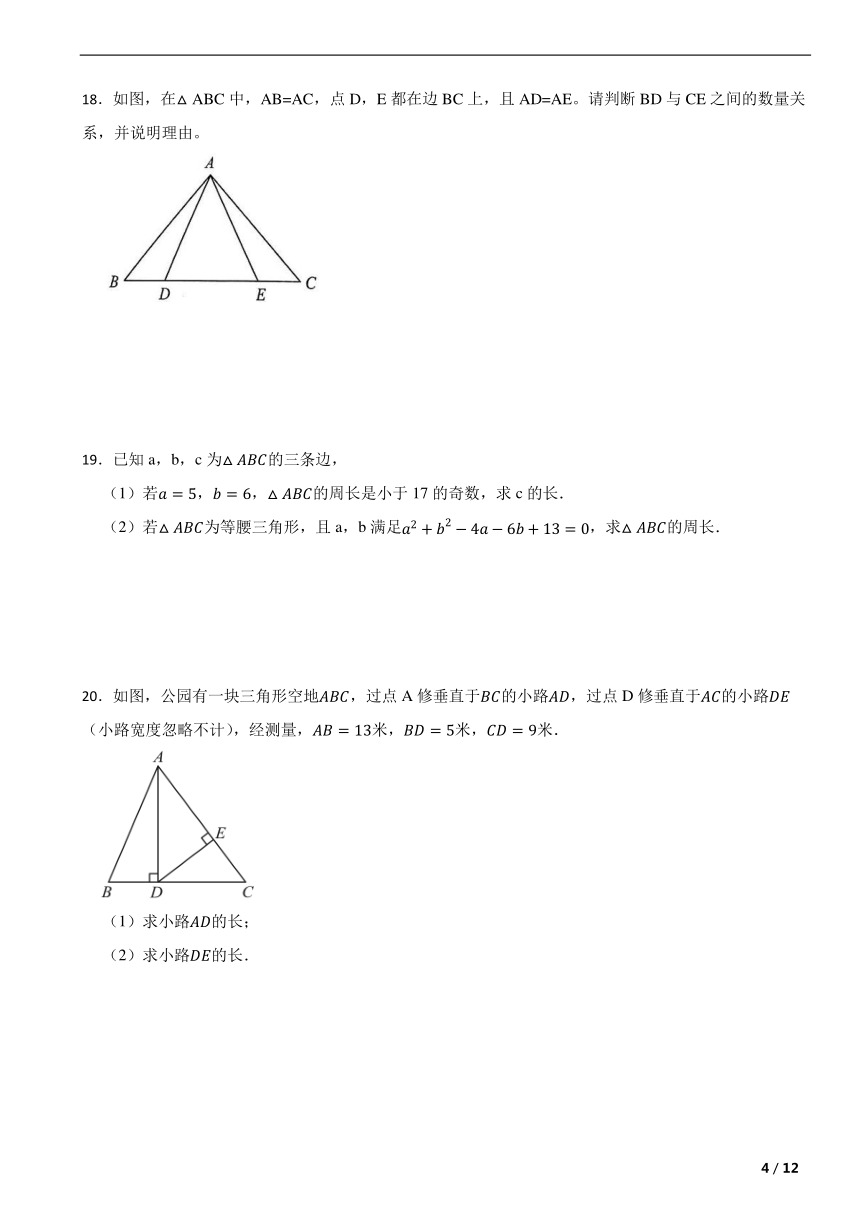
16.如图,中,,,,平分,动点M从点A出发,以每秒的速度沿边匀速运动,连接,当是以为腰的等腰三角形时,点M的运动时间为 秒.
三、解答题
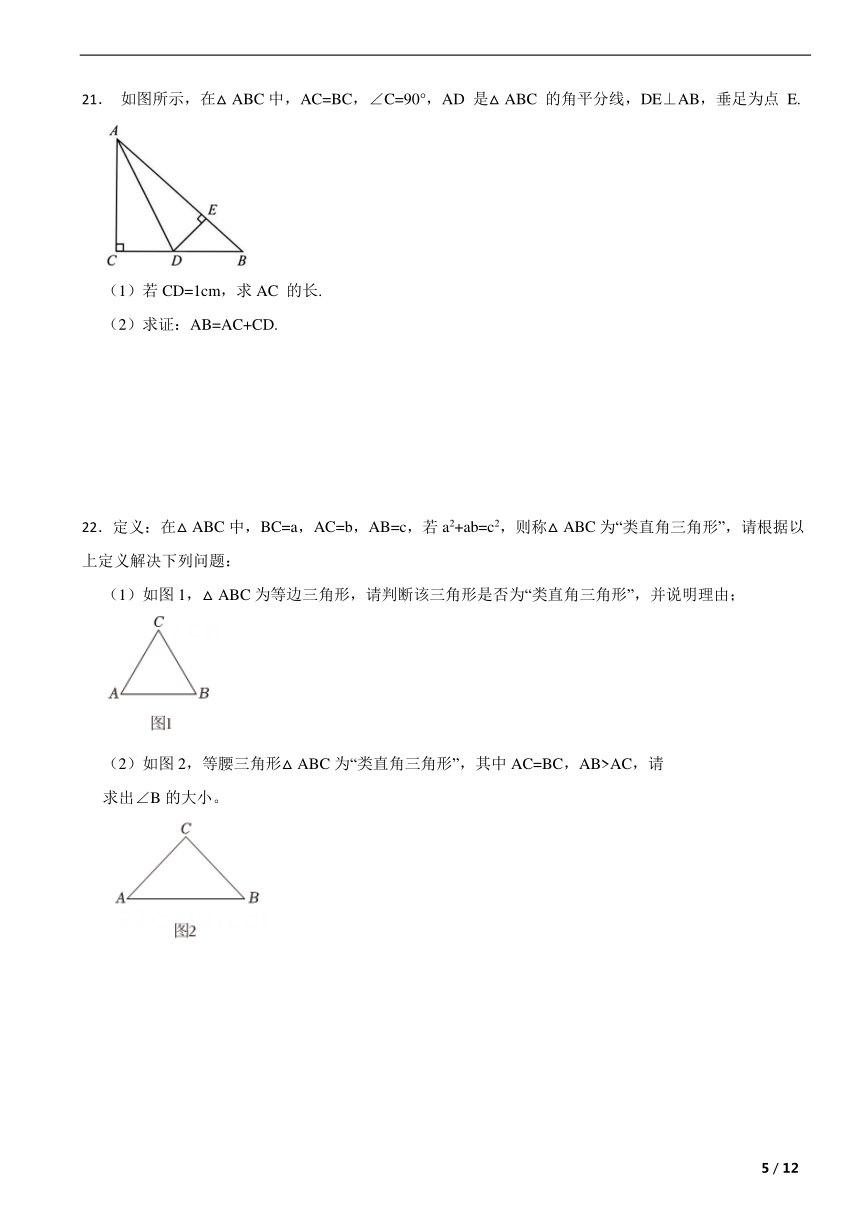
17.如图,在正方形网格中点A,B, C均为格点,接要求作图(保留作图痕迹,不写作法):
(1)作出 ABC关于直线1的对称图形 A'BC':
(2)求 ABC的面积;
(3)在直线1上找一点D, 使AD+CD最小.
18.如图,在△ABC中,AB=AC,点D,E都在边BC上,且AD=AE。请判断BD与CE之间的数量关系,并说明理由。
19.已知a,b,c为的三条边,
(1)若,,的周长是小于17的奇数,求c的长.
(2)若为等腰三角形,且a,b满足,求的周长.
20.如图,公园有一块三角形空地,过点A修垂直于的小路,过点D修垂直于的小路(小路宽度忽略不计),经测量,米,米,米.
(1)求小路的长;
(2)求小路的长.
21. 如图所示,在△ABC中,AC=BC,∠C=90°,AD 是△ABC 的角平分线,DE⊥AB,垂足为点 E.
(1)若CD=1cm,求AC 的长.
(2)求证:AB=AC+CD.
22.定义:在△ABC中,BC=a,AC=b,AB=c,若a2+ab=c2,则称△ABC为“类直角三角形”,请根据以上定义解决下列问题:
(1)如图1,△ABC为等边三角形,请判断该三角形是否为“类直角三角形”,并说明理由;
(2)如图2,等腰三角形△ABC为“类直角三角形”,其中AC=BC,AB>AC,请
求出∠B的大小。
23. 综合与实践
【问题情境】
如图1,有两张等腰三角形纸片ABC和AEF,其中AB=AC,AE=AF,∠BAC+∠EAF=180°.△AEF绕着A顺时针旋转,旋转角为(),点M为BF的中点.
【特例感知】
(1)如图1,当时,AM和CE的数量关系是 ;
(2)如图2,当时,连接AM,CE,请判断AM和CE的数量关系,并说明理由;
(3)【深入探究】
如图3,当为任意锐角时,连接AM,CE,则(2)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
参考答案
1.C
2.C
3.C
4.D
5.C
6.B
7.D
8.B
9.A
10.D
11.假
12.70°
13.3
14.1
15.3
16.或4或6
17.(1)解:如图所示, 即为所求;
(2)解: 的面积
(3)解:如图所示,点D即为所求.
18.解:猜想 :BD=CE
解法一:
过点A作AH⊥BC交BC于点H
∵AB=AC,AH⊥BC,
∴BH=CH。 ∵AD=AE,AH⊥BC, ∴DH=EH, ∴BH-DH=CH-EH,
∴BD=EC。
解法二: ∵AB=AC,
∴∠B=∠C,∵AD=AE,
∴∠ADE=∠AED,∴180°-∠ADE=180°-∠AED,
即∠ADB=∠AEC。在△ABD和△ACE中
∴△ABD≌△ACE(AAS),
∴BD=CE。
19.(1)解:∵a,b,c为的三条边,
∴,
∵,,
∴,
∵的周长是小于17的奇数,
∴,
∴,
∴,
∴且c是偶数,
∴或;
(2)解:∵,∴,
∴,
∵,
∴,
∴,
∴,
当腰长为2时,则该等腰三角形的三边长为2,2,3,
∵,
∴此时能构成三角形,
∴该三角形的周长为;
当腰长为3时,则该等腰三角形的三边长为2,3,3,
∵,
∴此时能构成三角形,
∴该三角形的周长为;
综上所述,该三角形的周长为7或8.
20.(1)解:∵AD⊥BC,
∴∠ADB=90°,
∵AB=13,BD=5,
∴根据勾股定理,得,
∴小路AD的长为12米;
(2)解:∵AD⊥BC,
∴∠ADC=90°,
由(1)得AD=12,
∵CD=9,
∴根据勾股定理,得,
∵DE⊥AC,
∴,
∴,
∴小路DE的长为7.2米.
21.(1)解:∵∠C=90°,AD是△ABC的角平分线,DE⊥AB,
∴DE=CD=1,
∵AC=BC,∠C=90°,
∴∠B=45°,
∴△BDE是等腰直角三角形,
∴,
∴
(2)证明:在Rt△ACD和Rt△AED中,
∴△ACD≌△AED(HL),
∴AC=AE.
由(1)得CD=DE=BE,
又∵AB=AE+EB,
∴AB=AC+CD
22.(1)解:等边三角形不是“类直角三角形”,理由如下:
设等边三角形的三边长分别为a,b,c,则a=b=c
∴a2+ab=c2+c2=2c2+c2,
∴等边三角形不是“类直角三角形”.
(2)解:等腰三角形是“类直角三角形”,,,
,且.
.
是直角三角形,且.
又,
是等腰直角三角形.
的度数为.
23.(1)AM=CE
(2)解:AM=CE
∵∠BAC+∠EAF=180°
∴∠CAE+∠BAF=180°
∵∠CAE=90°
∴∠CAE=∠BAF=90°
在△BAF和△CAE中
∴△BAF≌△CAE(SAS)
∴BF=CE
在Rt△BAF中
∵M为BF的中点
∴AM=BF
∴AM=CE
(3)解:成立
证明:延长BA到G,使得AG=AB
∴∠BAF+∠GAF=180°
∵∠BAC+∠EAF=180°
∴∠BAF+∠CAE=180°
∴∠GAF=∠CAE
∵AB=AC
∴AG=AC
在△GAF和△CAE中
∴△GAF≌△CAE(SAS)
∴GF=CE
∵M是BF的中点,AG=AB
∴AM=GF
∴AM=CE
1 / 1
一、选择题
1. 我国新能源汽车产业发展迅猛,取得了举世瞩目的成就,下列新能源汽车标志既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
2. 下列各组数据中,可以作为直角三角形三边长的是( )
A.1,2,3 B.2,3,4 C.3,4,5 D.4,5,6
3. 下列命题的逆命题正确的是( )
A.全等三角形的面积相等
B.全等三角形的周长相等
C.两个锐角互余的三角形是直角三角形
D.如果,那么
4.如图,在中,,,且,.则长为( )
A.1 B.2 C.3 D.4
5.等腰三角形底边长为,一腰上的中线把这个三角形的周长分为两部分,其差为,则该等腰三角形的腰长为( )
A. B. C. D.或
6.如图,在中,,,,则的长为( )
A.7 B.8 C.10 D.12
7.如图,已知,垂足为点O,,要根据“”证明,还需要添加的一个条件是( )
A. B. C. D.
8.在中,,,斜边上的高,则( )
A. B.6 C. D.9
9. 若三边长分别为,,,则的面积为( )
A.2 B.4 C. D.
10.如图,在等边中,,点,分别在边,上,且,连接,交于点,连接,则的最小值是( )
A.2 B.3 C. D.
二、填空题
11.已知命题“若,则”,其逆命题是 命题(填“真”或“假”).
12.在△ABC中,AB=AC。若∠A=40°,则∠C的大小为 .
13.如图,测量三角形纸片的尺寸,点,分别对应刻度尺上的刻度2和8,为的中点,若,则的长为 .
14. 如图,将两个完全相同的直角三角形纸板叠放在一起,。若,则CE的长度为 。
15.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若,大正方形的面积为25,则小正方形的边长为 .
16.如图,中,,,,平分,动点M从点A出发,以每秒的速度沿边匀速运动,连接,当是以为腰的等腰三角形时,点M的运动时间为 秒.
三、解答题
17.如图,在正方形网格中点A,B, C均为格点,接要求作图(保留作图痕迹,不写作法):
(1)作出 ABC关于直线1的对称图形 A'BC':
(2)求 ABC的面积;
(3)在直线1上找一点D, 使AD+CD最小.
18.如图,在△ABC中,AB=AC,点D,E都在边BC上,且AD=AE。请判断BD与CE之间的数量关系,并说明理由。
19.已知a,b,c为的三条边,
(1)若,,的周长是小于17的奇数,求c的长.
(2)若为等腰三角形,且a,b满足,求的周长.
20.如图,公园有一块三角形空地,过点A修垂直于的小路,过点D修垂直于的小路(小路宽度忽略不计),经测量,米,米,米.
(1)求小路的长;
(2)求小路的长.
21. 如图所示,在△ABC中,AC=BC,∠C=90°,AD 是△ABC 的角平分线,DE⊥AB,垂足为点 E.
(1)若CD=1cm,求AC 的长.
(2)求证:AB=AC+CD.
22.定义:在△ABC中,BC=a,AC=b,AB=c,若a2+ab=c2,则称△ABC为“类直角三角形”,请根据以上定义解决下列问题:
(1)如图1,△ABC为等边三角形,请判断该三角形是否为“类直角三角形”,并说明理由;
(2)如图2,等腰三角形△ABC为“类直角三角形”,其中AC=BC,AB>AC,请
求出∠B的大小。
23. 综合与实践
【问题情境】
如图1,有两张等腰三角形纸片ABC和AEF,其中AB=AC,AE=AF,∠BAC+∠EAF=180°.△AEF绕着A顺时针旋转,旋转角为(),点M为BF的中点.
【特例感知】
(1)如图1,当时,AM和CE的数量关系是 ;
(2)如图2,当时,连接AM,CE,请判断AM和CE的数量关系,并说明理由;
(3)【深入探究】
如图3,当为任意锐角时,连接AM,CE,则(2)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
参考答案
1.C
2.C
3.C
4.D
5.C
6.B
7.D
8.B
9.A
10.D
11.假
12.70°
13.3
14.1
15.3
16.或4或6
17.(1)解:如图所示, 即为所求;
(2)解: 的面积
(3)解:如图所示,点D即为所求.
18.解:猜想 :BD=CE
解法一:
过点A作AH⊥BC交BC于点H
∵AB=AC,AH⊥BC,
∴BH=CH。 ∵AD=AE,AH⊥BC, ∴DH=EH, ∴BH-DH=CH-EH,
∴BD=EC。
解法二: ∵AB=AC,
∴∠B=∠C,∵AD=AE,
∴∠ADE=∠AED,∴180°-∠ADE=180°-∠AED,
即∠ADB=∠AEC。在△ABD和△ACE中
∴△ABD≌△ACE(AAS),
∴BD=CE。
19.(1)解:∵a,b,c为的三条边,
∴,
∵,,
∴,
∵的周长是小于17的奇数,
∴,
∴,
∴,
∴且c是偶数,
∴或;
(2)解:∵,∴,
∴,
∵,
∴,
∴,
∴,
当腰长为2时,则该等腰三角形的三边长为2,2,3,
∵,
∴此时能构成三角形,
∴该三角形的周长为;
当腰长为3时,则该等腰三角形的三边长为2,3,3,
∵,
∴此时能构成三角形,
∴该三角形的周长为;
综上所述,该三角形的周长为7或8.
20.(1)解:∵AD⊥BC,
∴∠ADB=90°,
∵AB=13,BD=5,
∴根据勾股定理,得,
∴小路AD的长为12米;
(2)解:∵AD⊥BC,
∴∠ADC=90°,
由(1)得AD=12,
∵CD=9,
∴根据勾股定理,得,
∵DE⊥AC,
∴,
∴,
∴小路DE的长为7.2米.
21.(1)解:∵∠C=90°,AD是△ABC的角平分线,DE⊥AB,
∴DE=CD=1,
∵AC=BC,∠C=90°,
∴∠B=45°,
∴△BDE是等腰直角三角形,
∴,
∴
(2)证明:在Rt△ACD和Rt△AED中,
∴△ACD≌△AED(HL),
∴AC=AE.
由(1)得CD=DE=BE,
又∵AB=AE+EB,
∴AB=AC+CD
22.(1)解:等边三角形不是“类直角三角形”,理由如下:
设等边三角形的三边长分别为a,b,c,则a=b=c
∴a2+ab=c2+c2=2c2+c2,
∴等边三角形不是“类直角三角形”.
(2)解:等腰三角形是“类直角三角形”,,,
,且.
.
是直角三角形,且.
又,
是等腰直角三角形.
的度数为.
23.(1)AM=CE
(2)解:AM=CE
∵∠BAC+∠EAF=180°
∴∠CAE+∠BAF=180°
∵∠CAE=90°
∴∠CAE=∠BAF=90°
在△BAF和△CAE中
∴△BAF≌△CAE(SAS)
∴BF=CE
在Rt△BAF中
∵M为BF的中点
∴AM=BF
∴AM=CE
(3)解:成立
证明:延长BA到G,使得AG=AB
∴∠BAF+∠GAF=180°
∵∠BAC+∠EAF=180°
∴∠BAF+∠CAE=180°
∴∠GAF=∠CAE
∵AB=AC
∴AG=AC
在△GAF和△CAE中
∴△GAF≌△CAE(SAS)
∴GF=CE
∵M是BF的中点,AG=AB
∴AM=GF
∴AM=CE
1 / 1
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
