1.5.1 用三边关系判定三角形全等 课件(共25张PPT)
文档属性
| 名称 | 1.5.1 用三边关系判定三角形全等 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 12:33:35 | ||
图片预览








文档简介
第一章 三角形的初步知识
1.5.1 用三边关系判定三角形全等
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.了解三角形的稳定性,掌握三角形全等的条件——SSS.
2.会用SSS判定两个三角形全等.
3.由三角形的稳定性体会数学与实践的紧密联系,简单的推理过程培养学生严谨的逻辑思维.
02
新知导入
全等三角形
定义
A
B
C
D
E
F
能够重合的两个三角形
全等三角形
性质
∵ △ABC ≌△DEF
∴ AB=DE,AC=DF,BC=EF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形
判定
思考1:是否一定要满足三边相等,三个
角相等,才能保证两个三角形全等吗?
思考2:能否在上述六个条件中选择部分条件,简捷的判断两个三角形全等?
03
新知探究
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据了,能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗?
03
新知讲解
探究1 先画出一个△ABC,再画一个△DEF,使△ABC和△DEF满足上述条件中的一个(一边或一角相等)或两个(两边、一边一角或两角分别相等).你画出的△ABC和△DEF一定全等吗?
满足上述六个条件中的一个或者两个,△ABC和△DEF不一定全等。满足上述条件中的三个,能保证△ABC和△DEF全等吗?
03
新知讲解
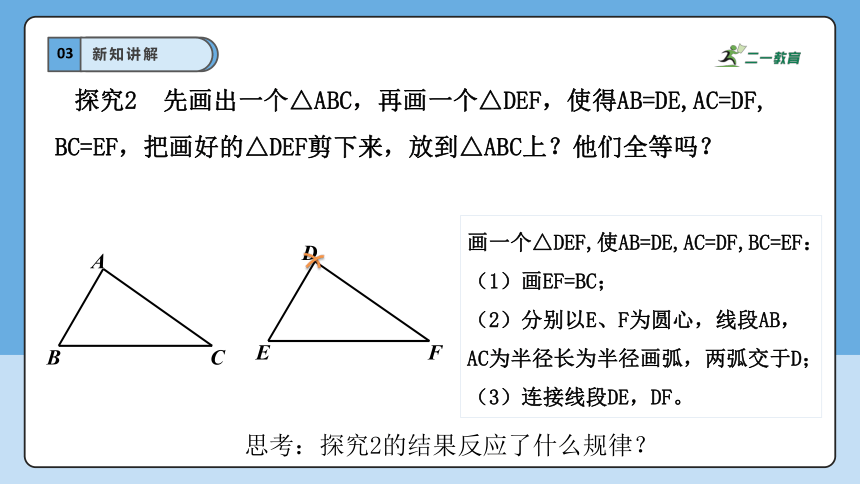
探究2 先画出一个△ABC,再画一个△DEF,使得AB=DE,AC=DF,
BC=EF,把画好的△DEF剪下来,放到△ABC上?他们全等吗?
A
B
C
D
E
F
画一个△DEF,使AB=DE,AC=DF,BC=EF:
(1)画EF=BC;
(2)分别以E、F为圆心,线段AB,AC为半径长为半径画弧,两弧交于D;
(3)连接线段DE,DF。
思考:探究2的结果反应了什么规律?
03
新知讲解
提炼概念
你有什么发现?
三角形全等的条件:三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
三条边对应相等的两个三角形
能重合
这两个三角形 全等
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
03
新知讲解
03
新知讲解
03
新知讲解
03
新知讲解
03
新知讲解
如图3,把两根木条的一端用螺栓固定在一起,木条可以自由移动,在转动过程中,连结另两个端点所成的三角形的形状、大小____________。如果把另两个端点用螺栓固定在第三根木条上(图4),那么构成的三角形的形状、大小就______________。
图3
图4
你得出什么结论?
随之改变
完全确定
03
新知讲解
当三角形的三条边长确定时,三角形的形状、大小完全被确定.
三角形的稳定性
(三角形的特有性质)
思考
你能用SSS来解释三角形的稳定性吗?
因为只要给定了一个三角形的三条边,那么根据全等三角形的判定可知,当两个三角形三条边相等时,两个三角形全等,形状和大小不变,只是位置发生了变化,这样的三角形唯一确定.?故三角形具有稳定性.
03
新知讲解
例如,房屋的人字架、大桥的钢梁、起重机的支架、自行车的车座等.采用三角形结构,起到稳固的作用.
三角形稳定性在生活中有哪些应用?
03
新知讲解
归纳概念
1.证明线段(或角相等)
转化
①说明两个三角形全等所需的条件应按对应边的顺序书写.
②结论中所出现的边必须在所证明的两个三角形中.
2.用结论说明两个三角形全等需注意
证明线段(或角)所在的两个三角形全等.
04
课堂练习
【知识技能类作业】必做题:
1.如图,建筑工人砌墙,在加入门框时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法是利用( )
A.长方形的四个角都是直角
B.两点之间线段最短
C.长方形的对称性
D.三角形的稳定性
D
04
课堂练习
【知识技能类作业】必做题:
2.如图所示,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出 个.
如图,这样的三角形最多可以画出4个
4
04
课堂练习
【综合拓展类作业】
3.如图,点A,D,C,F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
(2)∵∠A=55°,∠B=88°,
∴∠ACB=180°-∠A-∠B
=180°-55°-88°=37°.
又∵△ABC≌△DEF,
∴∠F=∠ACB=37°
(1)证明 ∵AD=CF(已知)
∴AD+CD=CF+DC,即AC=DF
在△ABC和△DEF中,
AB=DE(已知)
BC=EF(已知)
AC=DF ∴△ABC≌DEF(SSS)
05
课堂小结
1.三角形全等的判定
(边边边)
内容
有三边对应相等的两个三角形全等(简写成 “SSS”)
应用
思路分析
书写步骤
结合图形找隐含条件和现有条件,证准备条件
四步骤
2.三角形具有稳定性
06
作业布置
【知识技能类作业】必做题:
1.如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A.AD=CD B.AD=CF
C.BC∥EF D.DC=CF
B
06
作业布置
【知识技能类作业】选做题:
2.如图,△ABC和△DBC中,AB=CD,AC=BD,AC和DB相交于O,说出∠1=∠2的理由.
AB=CD
AC=BD
BC=CB
∴
△ABC≌△DCB
∴∠ABC=∠DCB,
∠ACB=∠DBC
∴∠1=∠2
解:
(已知)
(公共边)
(已知)
(SSS)
(全等三角形对应角相等)
∵∠1=∠ABC-∠DBC,
∠2=∠DCB-∠ACB,
A
B
C
D
O
2
1
在△ABC和△DCB中
06
作业布置
【综合拓展类作业】
3.如图,已知AB=CD,AD=CB,求证:∠B=∠D.
证明:连结AC,
∴ △ ABC≌ △ CDA(SSS)
∴ ∠B=∠D(全等三角形对应角相等)
问:1. 此题添加辅助线,若连结BD行吗?
2. 在原有条件下,还能推出什么结论?
A
B
C
D
A
B
C
D
AB=CD(已知)
AC=AC(公用边)
BC=AD(已知)
在△ABC和△ ADC中,
Thanks!
https://www.21cnjy.com/recruitment/home/fine
1.5.1 用三边关系判定三角形全等
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.了解三角形的稳定性,掌握三角形全等的条件——SSS.
2.会用SSS判定两个三角形全等.
3.由三角形的稳定性体会数学与实践的紧密联系,简单的推理过程培养学生严谨的逻辑思维.
02
新知导入
全等三角形
定义
A
B
C
D
E
F
能够重合的两个三角形
全等三角形
性质
∵ △ABC ≌△DEF
∴ AB=DE,AC=DF,BC=EF
∠A=∠D,∠B=∠E,∠C=∠F
全等三角形
判定
思考1:是否一定要满足三边相等,三个
角相等,才能保证两个三角形全等吗?
思考2:能否在上述六个条件中选择部分条件,简捷的判断两个三角形全等?
03
新知探究
为了庆祝国庆节,老师要求同学们回家制作三角形彩旗(如图),那么,老师应提供多少个数据了,能保证同学们制作出来的三角形彩旗全等呢?一定要知道所有的边长和所有的角度吗?
03
新知讲解
探究1 先画出一个△ABC,再画一个△DEF,使△ABC和△DEF满足上述条件中的一个(一边或一角相等)或两个(两边、一边一角或两角分别相等).你画出的△ABC和△DEF一定全等吗?
满足上述六个条件中的一个或者两个,△ABC和△DEF不一定全等。满足上述条件中的三个,能保证△ABC和△DEF全等吗?
03
新知讲解
探究2 先画出一个△ABC,再画一个△DEF,使得AB=DE,AC=DF,
BC=EF,把画好的△DEF剪下来,放到△ABC上?他们全等吗?
A
B
C
D
E
F
画一个△DEF,使AB=DE,AC=DF,BC=EF:
(1)画EF=BC;
(2)分别以E、F为圆心,线段AB,AC为半径长为半径画弧,两弧交于D;
(3)连接线段DE,DF。
思考:探究2的结果反应了什么规律?
03
新知讲解
提炼概念
你有什么发现?
三角形全等的条件:三边对应相等的两个三角形全等(简写成“边边边”或“SSS”)
三条边对应相等的两个三角形
能重合
这两个三角形 全等
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
03
新知讲解
03
新知讲解
03
新知讲解
03
新知讲解
03
新知讲解
如图3,把两根木条的一端用螺栓固定在一起,木条可以自由移动,在转动过程中,连结另两个端点所成的三角形的形状、大小____________。如果把另两个端点用螺栓固定在第三根木条上(图4),那么构成的三角形的形状、大小就______________。
图3
图4
你得出什么结论?
随之改变
完全确定
03
新知讲解
当三角形的三条边长确定时,三角形的形状、大小完全被确定.
三角形的稳定性
(三角形的特有性质)
思考
你能用SSS来解释三角形的稳定性吗?
因为只要给定了一个三角形的三条边,那么根据全等三角形的判定可知,当两个三角形三条边相等时,两个三角形全等,形状和大小不变,只是位置发生了变化,这样的三角形唯一确定.?故三角形具有稳定性.
03
新知讲解
例如,房屋的人字架、大桥的钢梁、起重机的支架、自行车的车座等.采用三角形结构,起到稳固的作用.
三角形稳定性在生活中有哪些应用?
03
新知讲解
归纳概念
1.证明线段(或角相等)
转化
①说明两个三角形全等所需的条件应按对应边的顺序书写.
②结论中所出现的边必须在所证明的两个三角形中.
2.用结论说明两个三角形全等需注意
证明线段(或角)所在的两个三角形全等.
04
课堂练习
【知识技能类作业】必做题:
1.如图,建筑工人砌墙,在加入门框时,常用木条EF固定长方形门框ABCD,使其不变形,这种做法是利用( )
A.长方形的四个角都是直角
B.两点之间线段最短
C.长方形的对称性
D.三角形的稳定性
D
04
课堂练习
【知识技能类作业】必做题:
2.如图所示,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出 个.
如图,这样的三角形最多可以画出4个
4
04
课堂练习
【综合拓展类作业】
3.如图,点A,D,C,F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:△ABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.
(2)∵∠A=55°,∠B=88°,
∴∠ACB=180°-∠A-∠B
=180°-55°-88°=37°.
又∵△ABC≌△DEF,
∴∠F=∠ACB=37°
(1)证明 ∵AD=CF(已知)
∴AD+CD=CF+DC,即AC=DF
在△ABC和△DEF中,
AB=DE(已知)
BC=EF(已知)
AC=DF ∴△ABC≌DEF(SSS)
05
课堂小结
1.三角形全等的判定
(边边边)
内容
有三边对应相等的两个三角形全等(简写成 “SSS”)
应用
思路分析
书写步骤
结合图形找隐含条件和现有条件,证准备条件
四步骤
2.三角形具有稳定性
06
作业布置
【知识技能类作业】必做题:
1.如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS”还需要添加一个条件是( )
A.AD=CD B.AD=CF
C.BC∥EF D.DC=CF
B
06
作业布置
【知识技能类作业】选做题:
2.如图,△ABC和△DBC中,AB=CD,AC=BD,AC和DB相交于O,说出∠1=∠2的理由.
AB=CD
AC=BD
BC=CB
∴
△ABC≌△DCB
∴∠ABC=∠DCB,
∠ACB=∠DBC
∴∠1=∠2
解:
(已知)
(公共边)
(已知)
(SSS)
(全等三角形对应角相等)
∵∠1=∠ABC-∠DBC,
∠2=∠DCB-∠ACB,
A
B
C
D
O
2
1
在△ABC和△DCB中
06
作业布置
【综合拓展类作业】
3.如图,已知AB=CD,AD=CB,求证:∠B=∠D.
证明:连结AC,
∴ △ ABC≌ △ CDA(SSS)
∴ ∠B=∠D(全等三角形对应角相等)
问:1. 此题添加辅助线,若连结BD行吗?
2. 在原有条件下,还能推出什么结论?
A
B
C
D
A
B
C
D
AB=CD(已知)
AC=AC(公用边)
BC=AD(已知)
在△ABC和△ ADC中,
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
