第四章 相似三角形单元练习(含答案)浙教版数学九年级上册
文档属性
| 名称 | 第四章 相似三角形单元练习(含答案)浙教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 548.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 22:46:22 | ||
图片预览


文档简介
第四章 相似三角形练习
一、选择题
1.下列各组线段中是成比例线段的是( )
A.1cm,2cm,3cm,4cm B.1cm,2cm,2cm,4cm
C.3cm,5cm,9cm,13cm D.1cm,2cm,2cm,3cm
2.如图,已知,,那么下列结论中,正确的是( )
A. B. C. D.
3.已知是的边上一点,连接,则下列不能判定的是( )
A. B. C. D.
4.若,相似比为,的周长为10,则的周长是( )
A.5 B.10 C.20 D.40
5.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学著作《九章算术》中的“井深几何”问题,它的题意可以由如图所示(单位:尺),已知井的截面图为矩形,设井深为尺,下列所列方程中,正确的是( )
A. B. C. D.
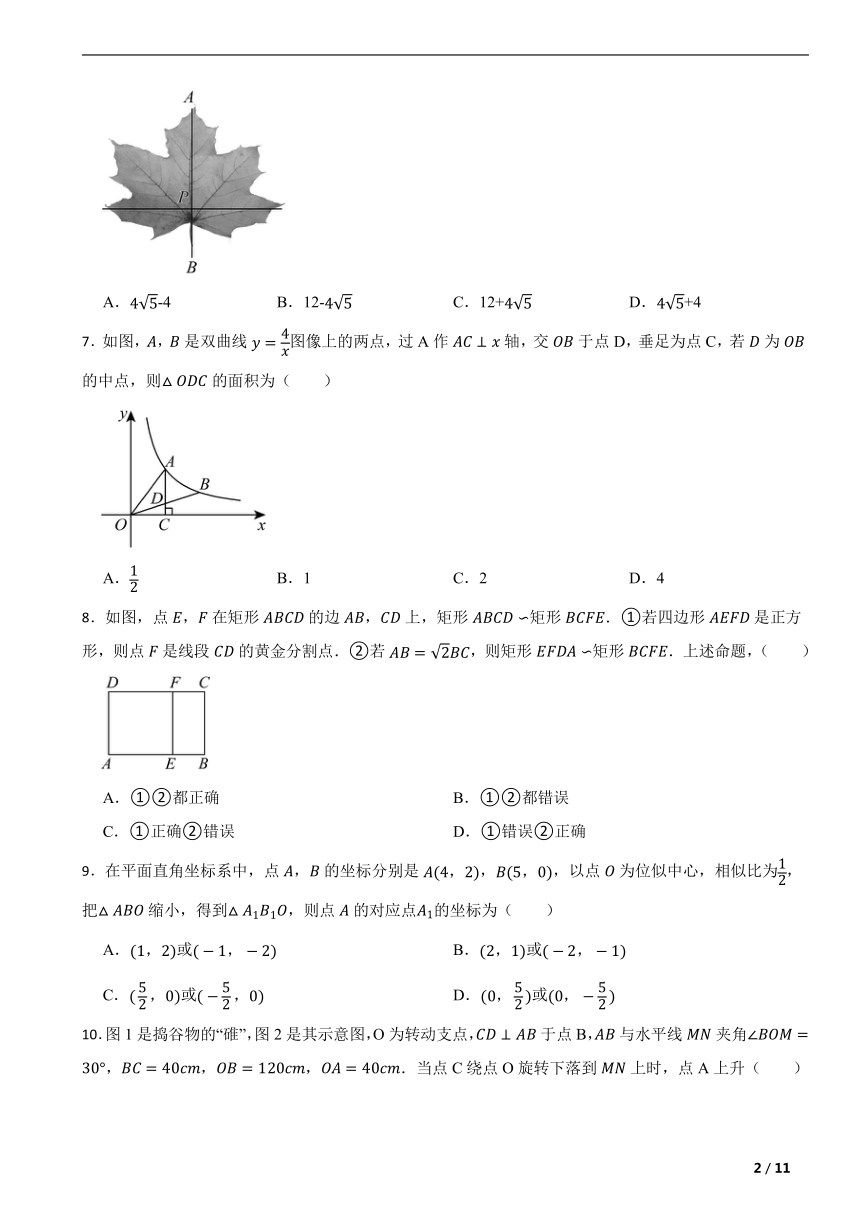
6.大自然巧夺天工,一片小心树叶也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP >PB),如果AP的长度为8cm,那么AB的长度是( )
A.-4 B.12- C.12+ D.+4
7.如图,,是双曲线图像上的两点,过A作轴,交于点D,垂足为点C,若为的中点,则的面积为( )
A. B.1 C.2 D.4
8.如图,点,在矩形的边,上,矩形矩形.①若四边形是正方形,则点是线段的黄金分割点.②若,则矩形矩形.上述命题,( )
A.①②都正确 B.①②都错误
C.①正确②错误 D.①错误②正确
9.在平面直角坐标系中,点,的坐标分别是,,以点为位似中心,相似比为,把缩小,得到,则点的对应点的坐标为( )
A.或 B.或
C.或 D.或
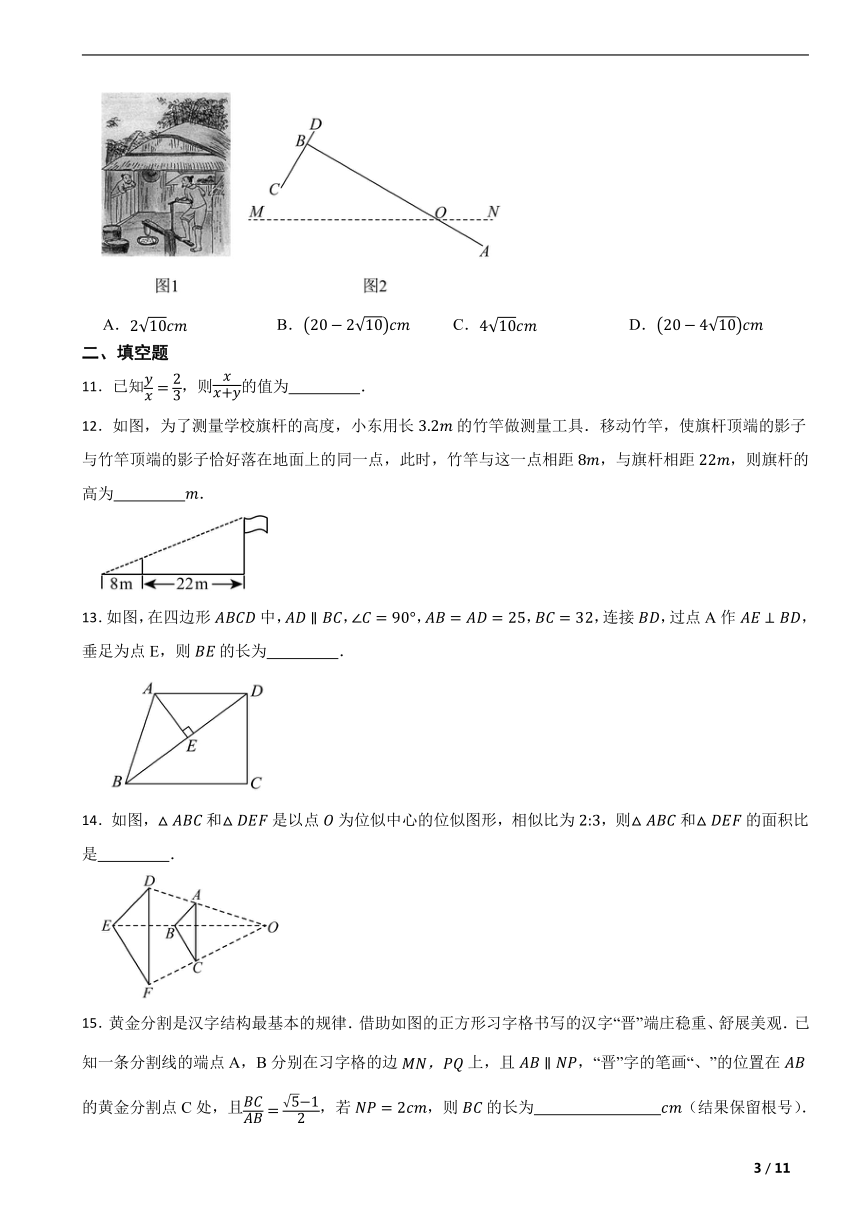
10.图1是捣谷物的“碓”,图2是其示意图,O为转动支点,于点B,与水平线夹角,,,.当点C绕点O旋转下落到上时,点A上升( )
A. B. C. D.
二、填空题
11.已知,则的值为 .
12.如图,为了测量学校旗杆的高度,小东用长的竹竿做测量工具.移动竹竿,使旗杆顶端的影子与竹竿顶端的影子恰好落在地面上的同一点,此时,竹竿与这一点相距,与旗杆相距,则旗杆的高为 .
13.如图,在四边形中,,,,,连接,过点A作,垂足为点E,则的长为 .
14.如图,和是以点为位似中心的位似图形,相似比为,则和的面积比是 .
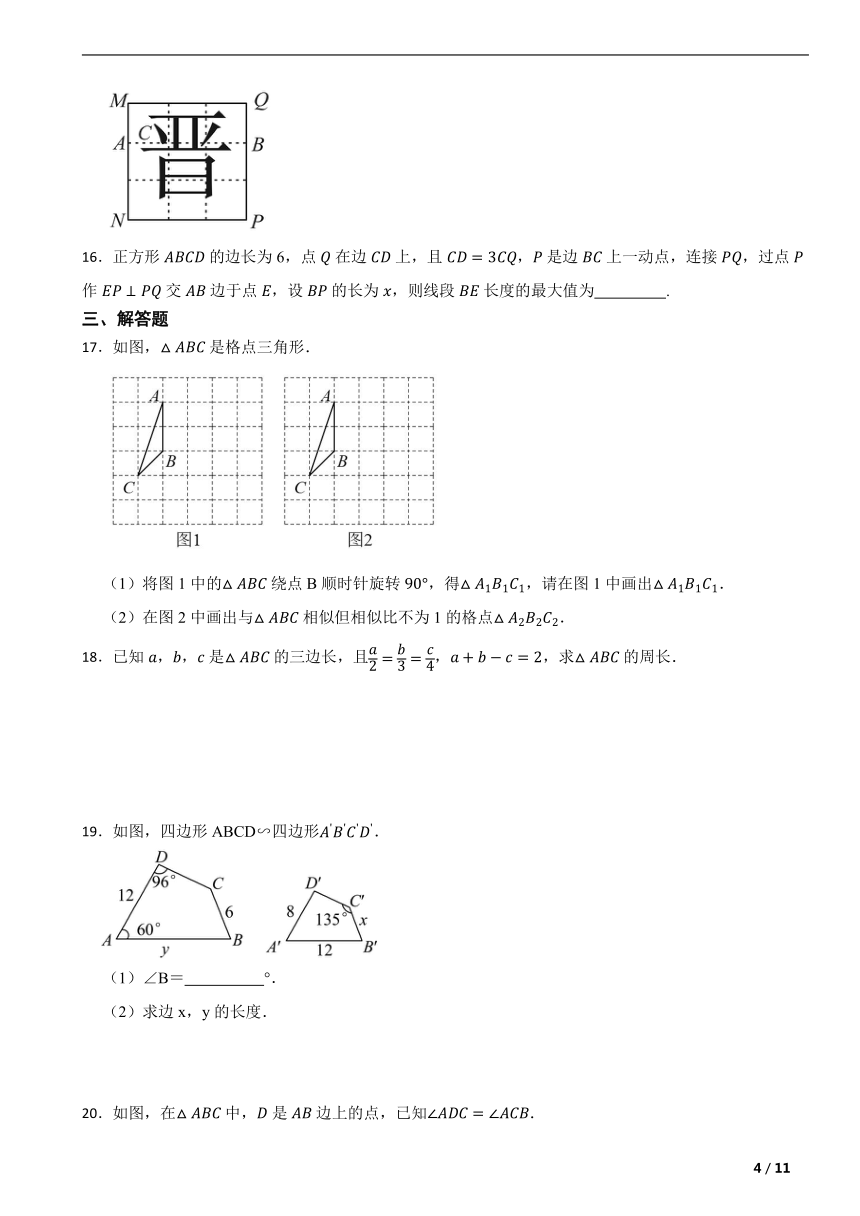
15.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在习字格的边上,且,“晋”字的笔画“、”的位置在的黄金分割点C处,且,若,则的长为 (结果保留根号).
16.正方形的边长为6,点在边上,且,是边上一动点,连接,过点作交边于点,设的长为,则线段长度的最大值为 .
三、解答题
17.如图,是格点三角形.
(1)将图1中的绕点B顺时针旋转,得,请在图1中画出.
(2)在图2中画出与相似但相似比不为1的格点.
18.已知,,是的三边长,且,,求的周长.
19.如图,四边形ABCD∽四边形.
(1)∠B= °.
(2)求边x,y的长度.
20.如图,在中,是边上的点,已知.
(1)求证:;
(2)若,,求的值.
21.如图,在中,点,分别在边,上,连接有以下四个条件:;;;.
(1)请你从中任选一个条件,使得∽,并说明理由.
注:如果选择多个结论分别作答,按第一个解答计分.
(2)在的前提下,若点为中点,,求线段的长.
22.如图,在矩形中,点E在边上,点F在对角线上,连接交于点O,且.
(1)求证:;
(2)判断与是否相似,并说明理由;
(3)若,,,求的长.
23.【项目式学习】
项目主题:学科融合—用数学的眼光观察世界
项目背景:学习完相似三角形性质后,某学校科学小组的同学们尝试用数学的知识和方法来研究凸透镜成像规律.
项目素材:
素材一:凸透镜成像规律:()表示凸透镜的焦距,()表示物体到凸透镜的距离,()表示像到凸透镜的距离,规律如下表
物体到凸透镜距离u 像到凸透镜距离v 像的大小 像的正倒
缩小 倒立
等大 倒立
放大 倒立
与物同侧 放大 正立
素材二:透镜成像中,光路图的规律:通过透镜中心的光线不发生改变;平行于主光轴的光线经过折射后光线经过焦点.
项目任务:
(1)任务一:凸透镜的焦距为,蜡烛的高为,离透镜中心的距离是时,请你利用所学的知识填空:①_________, ②_________,③ _________;
(2)任务二:某实验小组取焦距 为的凸透镜,高度是的蜡烛,设置物距时,测量蜡烛的成像的高,
①以为自变量,为因变量,写出与的关系式: ;
②当时,随的增大而 (选填“增大”或“减小”)
(提示:可在平面直角坐标系中作出函数的图象,不计分).
参考答案
1.B
2.A
3.D
4.C
5.D
6.D
7.A
8.A
9.B
10.D
11.
12.
13.20
14.
15.或
16.
17.(1)解:如图,△A1B1C1就是所求的三角形;
(2)解:如图,△A2B2C2就是所求的三角形;
18.解:设,则,,.
∵,
,解得.
的周长为.
答:的周长为18.
19.(1)
(2),
20.(1)证明:,,
(2)解:,
,
.
21.(1),
理由:,,
,
,
∽
注:答案不唯一,如选择;
(2),
,
点为中点,
,
∽,
,
,
,
,
线段的长为
22.(1)证明:∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:与相似,
理由是:∵,
∴;
(3)解:延长交于点G,
∵,
∴,
∴,
又∵,
∴,
∴
∵,
∴,
∴,
∴,
解得,
∴
23.(1),,;
(2)①;
②减小
1 / 1
一、选择题
1.下列各组线段中是成比例线段的是( )
A.1cm,2cm,3cm,4cm B.1cm,2cm,2cm,4cm
C.3cm,5cm,9cm,13cm D.1cm,2cm,2cm,3cm
2.如图,已知,,那么下列结论中,正确的是( )
A. B. C. D.
3.已知是的边上一点,连接,则下列不能判定的是( )
A. B. C. D.
4.若,相似比为,的周长为10,则的周长是( )
A.5 B.10 C.20 D.40
5.“今有井径五尺,不知其深,立五尺木于井上,从木末望水岸,入径四寸,问井深几何?”这是我国古代数学著作《九章算术》中的“井深几何”问题,它的题意可以由如图所示(单位:尺),已知井的截面图为矩形,设井深为尺,下列所列方程中,正确的是( )
A. B. C. D.
6.大自然巧夺天工,一片小心树叶也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP >PB),如果AP的长度为8cm,那么AB的长度是( )
A.-4 B.12- C.12+ D.+4
7.如图,,是双曲线图像上的两点,过A作轴,交于点D,垂足为点C,若为的中点,则的面积为( )
A. B.1 C.2 D.4
8.如图,点,在矩形的边,上,矩形矩形.①若四边形是正方形,则点是线段的黄金分割点.②若,则矩形矩形.上述命题,( )
A.①②都正确 B.①②都错误
C.①正确②错误 D.①错误②正确
9.在平面直角坐标系中,点,的坐标分别是,,以点为位似中心,相似比为,把缩小,得到,则点的对应点的坐标为( )
A.或 B.或
C.或 D.或
10.图1是捣谷物的“碓”,图2是其示意图,O为转动支点,于点B,与水平线夹角,,,.当点C绕点O旋转下落到上时,点A上升( )
A. B. C. D.
二、填空题
11.已知,则的值为 .
12.如图,为了测量学校旗杆的高度,小东用长的竹竿做测量工具.移动竹竿,使旗杆顶端的影子与竹竿顶端的影子恰好落在地面上的同一点,此时,竹竿与这一点相距,与旗杆相距,则旗杆的高为 .
13.如图,在四边形中,,,,,连接,过点A作,垂足为点E,则的长为 .
14.如图,和是以点为位似中心的位似图形,相似比为,则和的面积比是 .
15.黄金分割是汉字结构最基本的规律.借助如图的正方形习字格书写的汉字“晋”端庄稳重、舒展美观.已知一条分割线的端点A,B分别在习字格的边上,且,“晋”字的笔画“、”的位置在的黄金分割点C处,且,若,则的长为 (结果保留根号).
16.正方形的边长为6,点在边上,且,是边上一动点,连接,过点作交边于点,设的长为,则线段长度的最大值为 .
三、解答题
17.如图,是格点三角形.
(1)将图1中的绕点B顺时针旋转,得,请在图1中画出.
(2)在图2中画出与相似但相似比不为1的格点.
18.已知,,是的三边长,且,,求的周长.
19.如图,四边形ABCD∽四边形.
(1)∠B= °.
(2)求边x,y的长度.
20.如图,在中,是边上的点,已知.
(1)求证:;
(2)若,,求的值.
21.如图,在中,点,分别在边,上,连接有以下四个条件:;;;.
(1)请你从中任选一个条件,使得∽,并说明理由.
注:如果选择多个结论分别作答,按第一个解答计分.
(2)在的前提下,若点为中点,,求线段的长.
22.如图,在矩形中,点E在边上,点F在对角线上,连接交于点O,且.
(1)求证:;
(2)判断与是否相似,并说明理由;
(3)若,,,求的长.
23.【项目式学习】
项目主题:学科融合—用数学的眼光观察世界
项目背景:学习完相似三角形性质后,某学校科学小组的同学们尝试用数学的知识和方法来研究凸透镜成像规律.
项目素材:
素材一:凸透镜成像规律:()表示凸透镜的焦距,()表示物体到凸透镜的距离,()表示像到凸透镜的距离,规律如下表
物体到凸透镜距离u 像到凸透镜距离v 像的大小 像的正倒
缩小 倒立
等大 倒立
放大 倒立
与物同侧 放大 正立
素材二:透镜成像中,光路图的规律:通过透镜中心的光线不发生改变;平行于主光轴的光线经过折射后光线经过焦点.
项目任务:
(1)任务一:凸透镜的焦距为,蜡烛的高为,离透镜中心的距离是时,请你利用所学的知识填空:①_________, ②_________,③ _________;
(2)任务二:某实验小组取焦距 为的凸透镜,高度是的蜡烛,设置物距时,测量蜡烛的成像的高,
①以为自变量,为因变量,写出与的关系式: ;
②当时,随的增大而 (选填“增大”或“减小”)
(提示:可在平面直角坐标系中作出函数的图象,不计分).
参考答案
1.B
2.A
3.D
4.C
5.D
6.D
7.A
8.A
9.B
10.D
11.
12.
13.20
14.
15.或
16.
17.(1)解:如图,△A1B1C1就是所求的三角形;
(2)解:如图,△A2B2C2就是所求的三角形;
18.解:设,则,,.
∵,
,解得.
的周长为.
答:的周长为18.
19.(1)
(2),
20.(1)证明:,,
(2)解:,
,
.
21.(1),
理由:,,
,
,
∽
注:答案不唯一,如选择;
(2),
,
点为中点,
,
∽,
,
,
,
,
线段的长为
22.(1)证明:∵四边形是矩形,
∴,
∴,
∵,
∴,
∴,
∴;
(2)解:与相似,
理由是:∵,
∴;
(3)解:延长交于点G,
∵,
∴,
∴,
又∵,
∴,
∴
∵,
∴,
∴,
∴,
解得,
∴
23.(1),,;
(2)①;
②减小
1 / 1
同课章节目录
