1.5.3 三角形全等的判定 教案

中小学教育资源及组卷应用平台
分课时教学设计
第10课时《1.5.3 三角形全等的判定 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．
学习者分析 AAA，SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
教学目标 1．掌握角边角公理、角角边公理内容． 2．能应用角边角公理及其推论说明两个三角形全等．
教学重点 本节教学的重点是两个三角形全等的条件：两个角和其夹边对应相等的两个三角形全等．两角及其中一个角的对边对应相等的两个三角形全等．
教学难点 例题证明的思路较复杂，是本节教学的难点．
学习活动设计
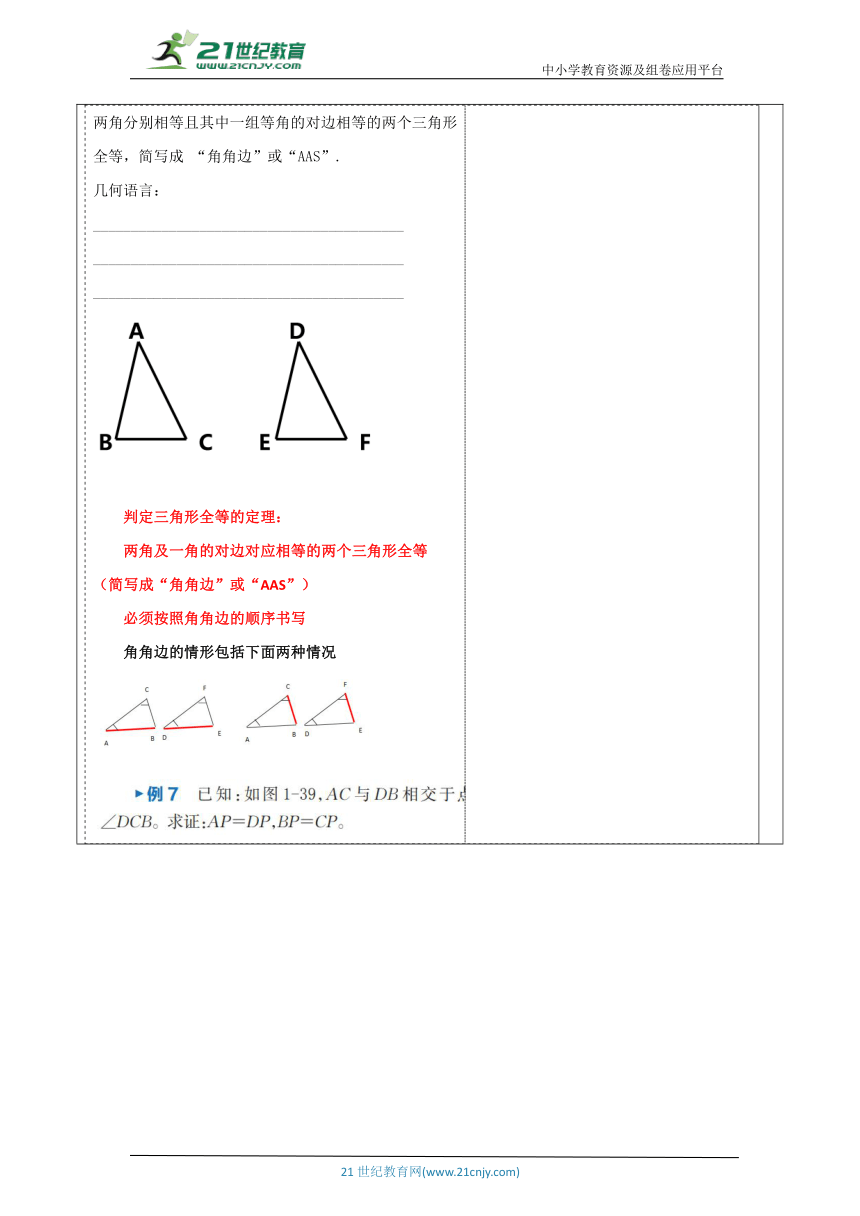
教师活动学生活动环节一：引入新课 复习回顾： 我们已经知道，三角形全等的判定条件有哪些 _________________________________ 那除了这两个条件，满足另一些条件的两个三角形是否也可能全等呢？今天我们就来探究三角形全等的另一些条件。 一张教学用的三角形硬纸板不小心被撕坏了，你能制作一张与原来同样大小的新教具吗？能恢复原来三角形的原貌吗 由前面的讨论我们知道，如果给出一个三角形三条边的长度，那么 由此得到的三角形是全等的。 如果已知一个三角形的两角及一边，那么有几种可能的情况呢？ 每种情况下得到的三角形全等吗？ 学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，从生活引入，通过提问题的方式，激发学生思考，进而讲授新知． 环节二：新知探究教师活动2： 【总结归纳】 两角及其夹边分别相等的两个三角形全等，简写成“______”或“______”. 几何语言： _________________________ _________________________ _________________________ 两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”. 学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．使学生经历探索三角形全等条件的过程,体会如何探索研究问题,并初步体会分类思想,提高学生分析问题和解决问题的能力． 环节三：典例精析 议一议 如果“两角及一边”条件中的边是其中一角的对边，情况会怎样呢？ 你能将它转化为“做一做”中的条件吗？ 【总结归纳】 两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成 “角角边”或“AAS”. 几何语言： _________________________________________ _________________________________________ _________________________________________ 判定三角形全等的定理： 两角及一角的对边对应相等的两个三角形全等 （简写成“角角边”或“AAS”） 必须按照角角边的顺序书写 角角边的情形包括下面两种情况 学生活动3： 参与教师分析和讲例题． 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，使学生经历探索三角形全等条件的过程,体会如何探索研究问题,并初步体会分类思想,提高学生分析问题和解决问题的能力．
板书设计
课堂练习 【知识技能类作业】 必做题： 1.如图，给出下列四个条件，不能判断△ABC≌△A′B′C′的是（　　）
①∠B=∠B′②∠C=∠C′
③AC=A′C′④BC=B′C′． A．①②③ B．①②④ C．①③④ D．②③④ 选做题： 如图∠ACB=∠DFE，BC=EF，请添加一个条件 ，（写出一个即可），能使△ABC≌△DEF 【综合拓展类作业】 3.王老师的一块三角形教学用玻璃不小心打破了（如图），他想再到玻璃店划一块，为了方便他只要带哪一块就可以了
课堂总结
作业设计 【知识技能类作业】 必做题： 1.如图，∠CAD=∠BAE，∠ACB=∠ADE，AB=AE， 则可判定（　） A．△AEF≌△ABD B．△ABC≌△AED C．△ADC≌△AFD D．以上答案都不对 选做题： 2．如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB＝AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD (　 　) A．∠B＝∠C B．AD＝AE C．BD＝CE D．BE＝CD 【综合拓展类作业】 3.点B，F，C，E在一条直线上，FB＝CE，AB∥ED，AC∥FD.求证：AC＝DF.
教学反思
21世纪教育网(www.21cnjy.com)