【章节考点培优】2.3有理数的乘法-2025-2026学年七年级上册数学浙教版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】2.3有理数的乘法-2025-2026学年七年级上册数学浙教版(2024)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 97.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 20:51:57 | ||
图片预览




文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优浙教版(2024)
第2章 有理数的运算 2.3 有理数的乘法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.有理数a,b在数轴上的位置如图所示,下列结论正确的是( )
A. B. C. D.
2.有理数在数轴上的位置如图所示,下列式子成立的是( )
A. B. C. D.
3.计算的结果是( )
A.8 B. C.6 D.
4.下列运算中,结果为负数的是( )
A. B.
C. D.
5.有理数a,b在数轴上的对应点如图所示,下列式子:①;②;③;④;⑤,其中正确的个数是( )
A.1 B.2 C.3 D.4
6.1.8的倒数是
A. B.- C. D.-
7.如果a+b>0,ab<0,则( )
A.a>0,b>0 B.a>0,b<0,|a|>|b|
C.a<0,b<0 D.a<0,b>0,|a|>|b|
8.多项式 的各项系数之积是( )
A. B.- C.3 D.-3
9.下列说法正确的是( )
A.|-2|与2互为相反数 B.与互为倒数
C.> D.是无理数
10.已知:,则( )
A. B. C. D.
二、填空题
11.绝对值小于π的所有正整数的积等于 .
12.一个数的倒数就是它本身,这个数是 .
13.﹣ 的倒数是 .
14.绝对值最小的数是 ;倒数等于它本身的数是 .
15.如果规定符号“※”的意义是a※b=a·a·b,那么5※(-2)= .
16.在某次比赛中,5位选手进入决赛环节,决赛赛制为单循环形式(每两位选手之间都赛一场).每位选手胜一场得3分.负一场得0分,平局得1分.已知这次比赛最终结果没有并列第一名,获得第一名的选手的成绩记为(分),则的最小值为 ;当获得第一名的选手的成绩恰好为最小值时,决赛环节的平局总数至少为 场.
三、计算题
17.简便计算:
(1)
(2)
四、解答题
18.已知:a,b互为倒数,c,d互为相反数,x的绝对值是2,求 的值.
19.学习有理数得乘法后,老师给同学们这样一道题目:计算:,看谁算的又快又对,有两位同学的解法如下:
小明:原式;
小军:原式;
(1)对于以上两种解法,你认为谁的解法较好?
(2)用你认为最合适的方法计算:.
20.计算:(-36).
21. 结合具体的数,通过特例进行归纳,然后判断下列说法是否正确. 如果认为正确,请说明理由; 如果认为错误,请举出反例.
(1) 任何数都不等于它的相反数;
(2)互为相反数的两个数的同一正偶数次幂相等;
(3) 如果a大于b,那么a的倒数小于b的倒数.
22.小华有5张写着不同数的卡片如下,请你按要求抽出卡片,完成下列各题:
(1)从中抽出2张卡片,使这2张卡片上的数乘积最大,最大值是______;
(2)从中抽出2张卡片,使这2张卡片上的数相除的商最小,最小值是______;
(3)从中抽出4张卡片,用学过的运算方法使结果为30,写出运算式子(至少写出两种).
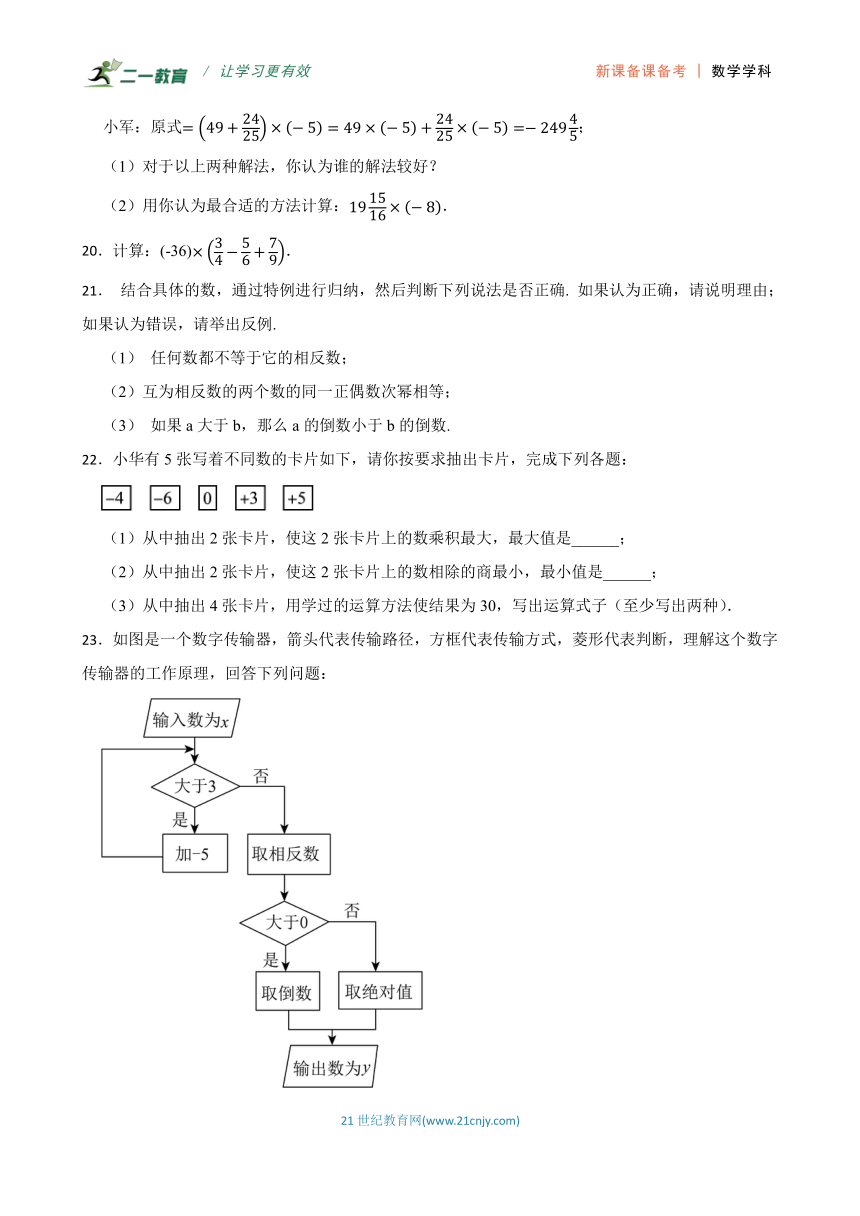
23.如图是一个数字传输器,箭头代表传输路径,方框代表传输方式,菱形代表判断,理解这个数字传输器的工作原理,回答下列问题:
(1)当时, ;当时, ;
(2)若输出的值为,则输入的为 ;
(3)若是自然数,请写出的所有可能值 .
参考答案及试题解析
1.B
2.B
3.B
4.B
5.B
6.A
【分析】根据互为倒数的两个数的乘积是1,用1除以一个数,即可求出它的倒数.
【解答】因为1÷1.8=,
所以1.8的倒数是.
故答案为:A.
【点评】此题主要考查了根据互为倒数的两个数的乘积是1求出一个数的倒数的能力
7.B
【解答】解:∵ab<0,
∴a、b异号,
又∵a+b>0,
∴正数的绝对值大于负数的绝对值.
故选:B.
【分析】由ab<0,根据有理数的乘法法则,可知a、b异号,又a+b>0,根据有理数的加法法则,可知正数的绝对值大于负数的绝对值.
8.D
【解答】解:多项式 的各项系数分别为 , ,
它们积为
故答案为:D
【分析】根据多项式的定义可得每项的系数,再利用有理数的乘法计算即可。
9.B
【解答】解:A、|-2|与2不互为相反数,则本项不符合题意,
B、与互为倒数,则本项符合题意,
C、,则本项不符合题意,
D、是有理数,则本项不符合题意,
故答案为:B.
【分析】根据互为相反数和倒数的性质即可判断A、B项;根据估计无理数的大小即可判断C项,根据无理数的定义即可判断D项.
10.C
11.6
【解答】∵绝对值小于π的所有正整数为:1,2,3,
∴绝对值小于π的所有正整数的积=1×2×3=6,
故答案为:6.
【分析】根据绝对值的性质写出符合题意的正整数,从而求出它们的积.
12.1或-1
【解答】解:∵
∴倒数是它本身的数是:1或-1.
故答案为:1或-1.
【分析】根据倒数的定义直接可得出答案.
13.﹣
【解答】解:(﹣ )×(﹣ )=1,
所以﹣ 的倒数是﹣ .
故答案为:﹣ .
【分析】根据倒数的定义即可解答.
14.0;±1
【解答】由绝对值的性质知正数的绝对值是本身,负数的绝对值是它的相反数,0的绝对值是0;1的倒数是1,-1的倒数是-1.
【分析】要牢记0的绝对值的特殊性,以及1,-1倒数的特殊性。
15.-50
【解答】解:由题意得
5※(-2)=5×5×(-2)=-5×5×2=-50
故答案为:-50.
【分析】根据定义新运算,列出乘法算式,再根据有理数的乘法法则算出结果即可。
16.6;4
17.(1)解:
=
=
=5;
(2)解:
=
=
=
=
【分析】(1)利用乘法的分配律先简便计算,然后进行加减运算即可;
(2)利用乘法的分配律先简便计算,然后进行减法运算即可.
18.解:由已知可得,
, , ,得 ,
【分析】根据a、b互为倒数得出ab=1,根据 c,d互为相反数得出c+d=1, 根据x的绝对值是2, 得出x2=4,最后代入原式求值即可.
19.(1)解:对于以上两种解法,小明使用了先求解括号内的值,在利用有理数的乘法,计算结果;
小军的解法中,使用了有理数运算的结合律,更容易运算,所以小军的解法较好.
(2)解:由
.
【分析】(1)本题考查了有理数乘法运算律,结合计算的简便程度,解得得到判断;
(2)把带分数进行适当的转化,利用乘法的分配律进行计算,由此可把写成,然后利用乘法分配律进行计算,即可得解.
(1)解:对于以上两种解法,小军的解法较好,
故答案为:小军;
(2)解:
.
20.解:原式=(﹣36)×(﹣+)
=(﹣36)×
=﹣25.
故答案为:﹣25.
【分析】先把括号内的分式通分,化为最简后再算乘法.
21.(1)解:错, 0 的相反数是它本身.
(2)解:对, 理由: 互为相反数的两个数的同一偶数次方符号相同, 绝对值相等。
(3)解:错, 如 , 但 3 的倒数 大于 -4 的倒数 .
【分析】(1) 有理数中,只有0的相反数等于它本身;
(2)经过偶次幂的处理,相反数的两个数的符号都会被统一成正号;
(3)一个数的倒数与原数的符号相同,故只需要举出正数a与负数b就可以判断为不正确.
22.(1)24
(2)
(3),(答案不唯一).
23.(1),
(2)()
(3),,,
【解答】解:(1)根据这个数字传输器的工作原理,可知:
当时,
不大于,取相反数,得:,
不大于,取绝对值,得:,
当时,;
当时,
大于,加,得:,
大于,加,得:,
大于,加,得:,
大于,加,得:,
大于,加,得:,
不大于,取相反数,得:,
大于,取倒数,得:,
当时,;
解:(2):根据这个数字传输器的工作原理,可知:
若输出的值为,
没有倒数,是取绝对值而来,
取绝对值之前的值是:,
又是取相反数而来,取相反数之前的值是:,
是输入的经过若干次加而来,
即:(),
(),
故输入的为:(),
故答案为:();
解:(3)根据这个数字传输器的工作原理,通过验证、分析、总结,可以发现:
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当()时,,
当()时,,
当()时,,
当()时,,
当()时,,
若是自然数,则的所有可能值为:,,,,
【分析】本题主要考查了程序流程图与有理数计算,有理数大小比较,有理数的加法运算,相反数与绝对值的定义,以及求倒数等知识点及应用.
(1)根据这个数字传输器的工作原理和操作步骤正向推导,即可得出答案;
(2)根据这个数字传输器的工作原理和操作步骤反向推导,即可得出答案;
(3)将自然数逐个输入求得输出,通过观察、分析,计算,即可总结出规律.
(1)解:根据这个数字传输器的工作原理,可知:
当时,
不大于,
取相反数,得:,
不大于,
取绝对值,得:,
当时,;
当时,
大于,
加,得:,
大于,
加,得:,
大于,
加,得:,
大于,
加,得:,
大于,
加,得:,
不大于,
取相反数,得:,
大于,
取倒数,得:,
当时,;
故答案为:,;
(2)解:根据这个数字传输器的工作原理,可知:
若输出的值为,
没有倒数,
是取绝对值而来,
取绝对值之前的值是:,
又是取相反数而来,
取相反数之前的值是:,
是输入的经过若干次加而来,
即:(),
(),
故输入的为:(),
故答案为:();
(3)解:根据这个数字传输器的工作原理,通过验证、分析、总结,可以发现:
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当()时,,
当()时,,
当()时,,
当()时,,
当()时,,
若是自然数,则的所有可能值为:,,,,
故答案为:,,,.
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优浙教版(2024)
第2章 有理数的运算 2.3 有理数的乘法
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.有理数a,b在数轴上的位置如图所示,下列结论正确的是( )
A. B. C. D.
2.有理数在数轴上的位置如图所示,下列式子成立的是( )
A. B. C. D.
3.计算的结果是( )
A.8 B. C.6 D.
4.下列运算中,结果为负数的是( )
A. B.
C. D.
5.有理数a,b在数轴上的对应点如图所示,下列式子:①;②;③;④;⑤,其中正确的个数是( )
A.1 B.2 C.3 D.4
6.1.8的倒数是
A. B.- C. D.-
7.如果a+b>0,ab<0,则( )
A.a>0,b>0 B.a>0,b<0,|a|>|b|
C.a<0,b<0 D.a<0,b>0,|a|>|b|
8.多项式 的各项系数之积是( )
A. B.- C.3 D.-3
9.下列说法正确的是( )
A.|-2|与2互为相反数 B.与互为倒数
C.> D.是无理数
10.已知:,则( )
A. B. C. D.
二、填空题
11.绝对值小于π的所有正整数的积等于 .
12.一个数的倒数就是它本身,这个数是 .
13.﹣ 的倒数是 .
14.绝对值最小的数是 ;倒数等于它本身的数是 .
15.如果规定符号“※”的意义是a※b=a·a·b,那么5※(-2)= .
16.在某次比赛中,5位选手进入决赛环节,决赛赛制为单循环形式(每两位选手之间都赛一场).每位选手胜一场得3分.负一场得0分,平局得1分.已知这次比赛最终结果没有并列第一名,获得第一名的选手的成绩记为(分),则的最小值为 ;当获得第一名的选手的成绩恰好为最小值时,决赛环节的平局总数至少为 场.
三、计算题
17.简便计算:
(1)
(2)
四、解答题
18.已知:a,b互为倒数,c,d互为相反数,x的绝对值是2,求 的值.
19.学习有理数得乘法后,老师给同学们这样一道题目:计算:,看谁算的又快又对,有两位同学的解法如下:
小明:原式;
小军:原式;
(1)对于以上两种解法,你认为谁的解法较好?
(2)用你认为最合适的方法计算:.
20.计算:(-36).
21. 结合具体的数,通过特例进行归纳,然后判断下列说法是否正确. 如果认为正确,请说明理由; 如果认为错误,请举出反例.
(1) 任何数都不等于它的相反数;
(2)互为相反数的两个数的同一正偶数次幂相等;
(3) 如果a大于b,那么a的倒数小于b的倒数.
22.小华有5张写着不同数的卡片如下,请你按要求抽出卡片,完成下列各题:
(1)从中抽出2张卡片,使这2张卡片上的数乘积最大,最大值是______;
(2)从中抽出2张卡片,使这2张卡片上的数相除的商最小,最小值是______;
(3)从中抽出4张卡片,用学过的运算方法使结果为30,写出运算式子(至少写出两种).
23.如图是一个数字传输器,箭头代表传输路径,方框代表传输方式,菱形代表判断,理解这个数字传输器的工作原理,回答下列问题:
(1)当时, ;当时, ;
(2)若输出的值为,则输入的为 ;
(3)若是自然数,请写出的所有可能值 .
参考答案及试题解析
1.B
2.B
3.B
4.B
5.B
6.A
【分析】根据互为倒数的两个数的乘积是1,用1除以一个数,即可求出它的倒数.
【解答】因为1÷1.8=,
所以1.8的倒数是.
故答案为:A.
【点评】此题主要考查了根据互为倒数的两个数的乘积是1求出一个数的倒数的能力
7.B
【解答】解:∵ab<0,
∴a、b异号,
又∵a+b>0,
∴正数的绝对值大于负数的绝对值.
故选:B.
【分析】由ab<0,根据有理数的乘法法则,可知a、b异号,又a+b>0,根据有理数的加法法则,可知正数的绝对值大于负数的绝对值.
8.D
【解答】解:多项式 的各项系数分别为 , ,
它们积为
故答案为:D
【分析】根据多项式的定义可得每项的系数,再利用有理数的乘法计算即可。
9.B
【解答】解:A、|-2|与2不互为相反数,则本项不符合题意,
B、与互为倒数,则本项符合题意,
C、,则本项不符合题意,
D、是有理数,则本项不符合题意,
故答案为:B.
【分析】根据互为相反数和倒数的性质即可判断A、B项;根据估计无理数的大小即可判断C项,根据无理数的定义即可判断D项.
10.C
11.6
【解答】∵绝对值小于π的所有正整数为:1,2,3,
∴绝对值小于π的所有正整数的积=1×2×3=6,
故答案为:6.
【分析】根据绝对值的性质写出符合题意的正整数,从而求出它们的积.
12.1或-1
【解答】解:∵
∴倒数是它本身的数是:1或-1.
故答案为:1或-1.
【分析】根据倒数的定义直接可得出答案.
13.﹣
【解答】解:(﹣ )×(﹣ )=1,
所以﹣ 的倒数是﹣ .
故答案为:﹣ .
【分析】根据倒数的定义即可解答.
14.0;±1
【解答】由绝对值的性质知正数的绝对值是本身,负数的绝对值是它的相反数,0的绝对值是0;1的倒数是1,-1的倒数是-1.
【分析】要牢记0的绝对值的特殊性,以及1,-1倒数的特殊性。
15.-50
【解答】解:由题意得
5※(-2)=5×5×(-2)=-5×5×2=-50
故答案为:-50.
【分析】根据定义新运算,列出乘法算式,再根据有理数的乘法法则算出结果即可。
16.6;4
17.(1)解:
=
=
=5;
(2)解:
=
=
=
=
【分析】(1)利用乘法的分配律先简便计算,然后进行加减运算即可;
(2)利用乘法的分配律先简便计算,然后进行减法运算即可.
18.解:由已知可得,
, , ,得 ,
【分析】根据a、b互为倒数得出ab=1,根据 c,d互为相反数得出c+d=1, 根据x的绝对值是2, 得出x2=4,最后代入原式求值即可.
19.(1)解:对于以上两种解法,小明使用了先求解括号内的值,在利用有理数的乘法,计算结果;
小军的解法中,使用了有理数运算的结合律,更容易运算,所以小军的解法较好.
(2)解:由
.
【分析】(1)本题考查了有理数乘法运算律,结合计算的简便程度,解得得到判断;
(2)把带分数进行适当的转化,利用乘法的分配律进行计算,由此可把写成,然后利用乘法分配律进行计算,即可得解.
(1)解:对于以上两种解法,小军的解法较好,
故答案为:小军;
(2)解:
.
20.解:原式=(﹣36)×(﹣+)
=(﹣36)×
=﹣25.
故答案为:﹣25.
【分析】先把括号内的分式通分,化为最简后再算乘法.
21.(1)解:错, 0 的相反数是它本身.
(2)解:对, 理由: 互为相反数的两个数的同一偶数次方符号相同, 绝对值相等。
(3)解:错, 如 , 但 3 的倒数 大于 -4 的倒数 .
【分析】(1) 有理数中,只有0的相反数等于它本身;
(2)经过偶次幂的处理,相反数的两个数的符号都会被统一成正号;
(3)一个数的倒数与原数的符号相同,故只需要举出正数a与负数b就可以判断为不正确.
22.(1)24
(2)
(3),(答案不唯一).
23.(1),
(2)()
(3),,,
【解答】解:(1)根据这个数字传输器的工作原理,可知:
当时,
不大于,取相反数,得:,
不大于,取绝对值,得:,
当时,;
当时,
大于,加,得:,
大于,加,得:,
大于,加,得:,
大于,加,得:,
大于,加,得:,
不大于,取相反数,得:,
大于,取倒数,得:,
当时,;
解:(2):根据这个数字传输器的工作原理,可知:
若输出的值为,
没有倒数,是取绝对值而来,
取绝对值之前的值是:,
又是取相反数而来,取相反数之前的值是:,
是输入的经过若干次加而来,
即:(),
(),
故输入的为:(),
故答案为:();
解:(3)根据这个数字传输器的工作原理,通过验证、分析、总结,可以发现:
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当()时,,
当()时,,
当()时,,
当()时,,
当()时,,
若是自然数,则的所有可能值为:,,,,
【分析】本题主要考查了程序流程图与有理数计算,有理数大小比较,有理数的加法运算,相反数与绝对值的定义,以及求倒数等知识点及应用.
(1)根据这个数字传输器的工作原理和操作步骤正向推导,即可得出答案;
(2)根据这个数字传输器的工作原理和操作步骤反向推导,即可得出答案;
(3)将自然数逐个输入求得输出,通过观察、分析,计算,即可总结出规律.
(1)解:根据这个数字传输器的工作原理,可知:
当时,
不大于,
取相反数,得:,
不大于,
取绝对值,得:,
当时,;
当时,
大于,
加,得:,
大于,
加,得:,
大于,
加,得:,
大于,
加,得:,
大于,
加,得:,
不大于,
取相反数,得:,
大于,
取倒数,得:,
当时,;
故答案为:,;
(2)解:根据这个数字传输器的工作原理,可知:
若输出的值为,
没有倒数,
是取绝对值而来,
取绝对值之前的值是:,
又是取相反数而来,
取相反数之前的值是:,
是输入的经过若干次加而来,
即:(),
(),
故输入的为:(),
故答案为:();
(3)解:根据这个数字传输器的工作原理,通过验证、分析、总结,可以发现:
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当时,,
当()时,,
当()时,,
当()时,,
当()时,,
当()时,,
若是自然数,则的所有可能值为:,,,,
故答案为:,,,.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
