【章节考点培优】2.6有理数的混合运算-2025-2026学年七年级上册数学浙教版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】2.6有理数的混合运算-2025-2026学年七年级上册数学浙教版(2024)(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 82.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 21:01:51 | ||
图片预览




文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优浙教版(2024)
第2章 有理数的运算 2.6 有理数的混合运算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若等式2≤(﹣2)=0成立,则“≤”内的运算符号是( ).
A.+ B.﹣ C.× D.÷
2.下列计算正确的是( )
A. B.
C. D.
3.2020年3月抗击“新冠肺炎”居家学习期间,小华计划每天背诵6个汉语成语.将超过的个数记为正数,不足的个数记为负数,某一周连续5天的背诵记录如下:,则这5天他共背诵汉语成语( )
A.8个 B.14个 C.38个 D.36个
4.若a、b互为相反数,x、y互为倒数,则的值是( )
A.3 B.2 C.1 D.5
5.如图,某公园有一长方形广场,长为米,宽为米,在其两角修建半径均为米的扇形花坛,在广场中心修建一个直径为米的圆形喷泉水池,则该广场的空地面积为(取3)( ).
A. B. C. D.
6. 计算 结果是 ( )
A. B. C. D.- 7
7.在遵义拍摄的历史剧《伟大的转折》刚在央视一套热播,为新中国70周年献上了一份大礼.红军行军过程中需要用密码进行信息传输,其中一组密码规定:输入任意一对有理数 (a,b)后就转换得到一个新数a2+b-2,例如输入 (3,-1)就得到32+(-1)-2=6,也就得到了6对应的字.如果输入(-4,7),则得到的对应数字为( )
A.-11 B.21 C.23 D.11
8.用计算器计算时,下列说法错误的是( )
A.“计算 ”的按键顺序是 1 ab/c 2 ﹣ 1 ab/c 3 ab/c 4 =
B.“计算 ”的按键顺序是 3 EXP 5 ﹣ 2 8 =
C.“已知SinA=0.3,求锐角A”的按键顺序是DEL 2ndF sin 0 . 3 =
D.“计算 ”的按键顺序是1 ab/c 2 2ndF 5 =
9.随着2010年元旦的到来, 宁波市各大百货公司纷纷推出各种优惠以答谢顾客, 其中一家百货公司贴出的优惠标语是: 买200元物品, 送100元购物券, 买400元物品送200购物券,……依次类推; 于是小红陪着她的妈妈一起来到百货公司买东西, 没过多少时间小红就看中了一件衣服, 一问价钱需要650元. 她心想贵是贵了点,但是能送300元的购物券还是挺划算的, 于是就花650元把这件衣服买了, 同时也得到了300元购物券. 后来小红又用这310元购物券买了一双鞋子, 这时就没有购物券送了. 则下列优惠中, 与小红在这次购物活动中所享受的优惠最接近的是( )
A.5折 B.6折 C.7折 D.8折
10.规定“!”是一种运算符号,
其中1!=1,
2!=1×2,
3!=1×2×3,
4!=1×2×3×4,…
则 的值为( )
A.2014 B.2015 C.2016 D.2017
二、填空题
11. 10头大象1天的食品可供1000只老鼠吃600天,假定每头大象的食量都一样,每只老鼠的食量也相等,那么m头大象1天的食物可供100只老鼠吃 天.
12.若xyz<0,则 的值为
13.已知有理数a、b、c的和为0,且a=7,b=﹣2,则c= .
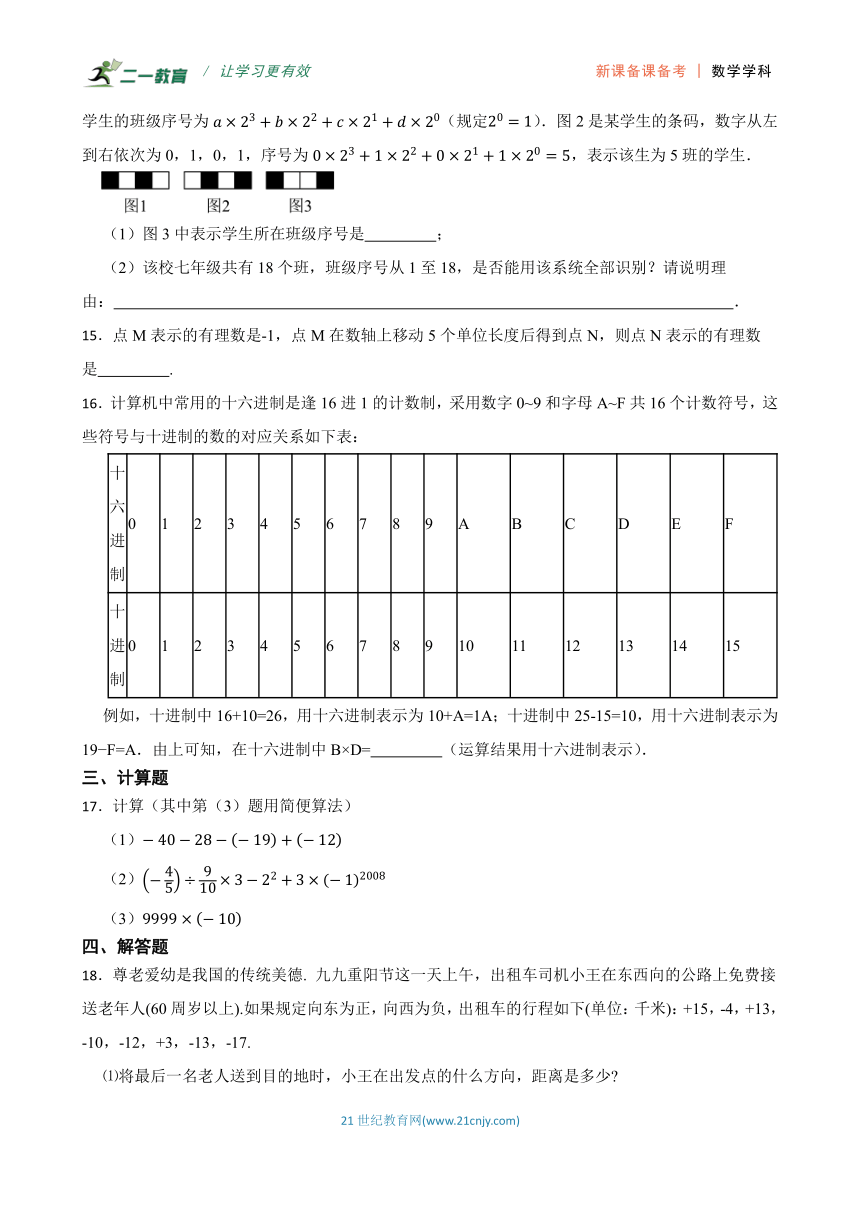
14.某校建立了一个身份识别系统,利用如图1(由四个小正方形组成)的条码可以对学生所在班级序号进行识别.黑色小正方形表示1,白色小正方形表示0将数字从左到右依次记为a,b,c,d,则学生的班级序号为(规定).图2是某学生的条码,数字从左到右依次为0,1,0,1,序号为,表示该生为5班的学生.
(1)图3中表示学生所在班级序号是 ;
(2)该校七年级共有18个班,班级序号从1至18,是否能用该系统全部识别?请说明理由: .
15.点M表示的有理数是-1,点M在数轴上移动5个单位长度后得到点N,则点N表示的有理数是 .
16.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 0 1 2 3 4 5 6 7 8 9 A B C D E F
十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例如,十进制中16+10=26,用十六进制表示为10+A=1A;十进制中25-15=10,用十六进制表示为19 F=A.由上可知,在十六进制中B×D= (运算结果用十六进制表示).
三、计算题
17.计算(其中第(3)题用简便算法)
(1)
(2)
(3)
四、解答题
18.尊老爱幼是我国的传统美德. 九九重阳节这一天上午,出租车司机小王在东西向的公路上免费接送老年人(60周岁以上).如果规定向东为正,向西为负,出租车的行程如下(单位:千米):+15,-4,+13,-10,-12,+3,-13,-17.
⑴将最后一名老人送到目的地时,小王在出发点的什么方向,距离是多少
⑵若出租车耗油量为0.07升/千米,这天上午小王的出租车共耗油多少升
19.出租车司机小王某天下午的一段时间内营运全是在南北走向的北海路上进行的。如果向南记作“+”,向北记作“-”,那么他这段时间内行车情况如下(单位: km。每次行车都有乘客):-4,+7,-2,-3,-8,+8。请解答下列问题:
(1)小王将最后一名乘客送到目的地时,在下午出车的出发地的什么方向 距下午出车的出发地多远
(2)若规定每次乘坐出租车的起步价是8元,且3 km以内(含 3km)只收起步价;若超过3km,除收起步价外,超过的每千米还需收1.8元。小王这段时间内收到乘客所给的车费共多少元
(3)若小王的出租车每千米耗油0.1L,每升汽油7元。不计汽车损耗的情况下,除去汽油钱,请你帮小王计算一下,这段时间内他赚了多少钱
20.上午出租车司机小王在东西向的公路上免费接送老师.如果规定向东为正,向西为负,出租车的行程如下 (单位:千米) :
(1) 最后一名老师送到目的地时,小王距出车地点的距离是多少
(2) 若汽车耗油量为0.4升/千米,这天上午汽车共耗油多少升
21.某校举行了以“珍爱生命、远离水患”为主题的知识竞赛.下表是善思小组6位同学参加此次竞赛的成绩(以100分为标准,超过100分记为“+”,不足100分记为“-”),请根据表中信息解决下列问题.
编号 1 2 3 4 5 6
知识竞赛成绩/分
(1)求这6位同学本次竞赛的最高得分.
(2)最高分超出最低分多少分?
(3)求这6位同学本次竞赛成绩的总分.
22.某校举办了“废纸回收,变废为宝”活动,各班收集的废纸均以5kg为标准,超过的部分记为“+”,不足的部分记为“-”,七年级六个班级的废纸收集情况如下表所示,统计员小虎不小心将一个数据弄脏看不清了,但他记得三班收集的废纸最少,且收集废纸最多的班级和最少的班级质量差4kg.
班级 一 二 三 四 五 六
超过(不足)(kg) +1 +2 -1.5 0 -1
(1)请你计算七年级六班同学收集废纸的质量;
(2)若本次活动收集废纸质量排名前三的班级可获得荣誉称号,请计算获得荣誉称号的班级收集废纸的总质量;
(3)若七年级六个班级将本次活动收集的废纸以1.5元/kg的价格集中卖出,求这些废纸卖出的总钱数.
23.如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为3,BC=2,AB=6.
(1)则点A对应的数是 、点B对应的数是 ;
(2)动点P、Q分别同时从A、C出发,分别以每秒8个单位和4个单位的速度沿数轴正方向运动.M在线段AP上,且AM=MP,N在线段CQ上,且 ,设运动时间为t(t>0).
①求点M、N对应的数(用含t的式子表示);
②猜想MQ的长度是否与t无关为定值,若为定值请求出该定值,若不为定值请说明理由;
③探究t为何值时,OM=2BN.
参考答案及试题解析
1.A
2.A
3.C
4.A
【解答】解:由题意得:,,
∴.
故选:A.
【分析】根据利用相反数,倒数的定义求出,,代入原式计算求解即可.
5.B
6.C
【解答】解:
.
故答案为:C.
【分析】首先计算第二个括号内的部分,然后将除法转换成乘法并计算即可.
7.B
【解答】解:∵输入(a,b)后,会得到一个新的有理数:a2+b-2,
∴输入(-4,7),得到的结果为:(-4)2+7-2=16+7-2=21,
故答案为:B.
【分析】根据新定义法则列出算式,再根据有理数的加减法法则即可算出答案.
8.D
【解答】解:A、“计算
”的按键顺序是 1 、ab/c 、2 、﹣ 、1 、ab/c 、3、 ab/c、 4 、= 、是正确的,不符题意;
B、“计算
”的按键顺序是 3、 EXP、 5 、﹣、 2 8 、=、是正确的,不符题意;
C、“已知SinA=0.3,求锐角A”的按键顺序是DEL、 2ndF、 sin、 0 . 3、 =、是正确的,不符题意;
D、“计算
”的按键顺序是1 、ab/c 、2 、
、 5、 =、原来的说法是错误的,符合题意;
故答案为:D.
【分析】根据计算器上分数、科学记数法、三角函数及乘方计算方法可得答案.
9.C
【分析】首先计算一下小红实际花了多少钱;650+310-300=660(元),如果不享受优惠则需要花;650+310=960(元),用实际花的钱÷不优惠花的钱,可得到打了几折.
【解答】
实际花钱数÷不优惠花钱数=(650+310-300)÷(650+310)=0.6875≈0.7,
∴小红在这次购物活动中所享受的优惠最接近的是7折.
故选:C.
【点评】此题主要考查了实际生活中的数学问题,解题关键是要读懂题目的意思,找出合适的等量关系.
10.D
【解答】解:根据题中的新定义得:原式= =2017,
故选D
【分析】原式根据题中的新定义化简,计算即可得到结果.
11.600m
【解答】解: m÷100=600m(天).
故答案为:600m.
【分析】根据已知10头大象1天的食品可供1000只老鼠吃600天,假定每头大象的食量都一样,每只老鼠的食量也相等,可求出那么m头大象1天的食品可供100只老鼠吃多少天.
12.-4或0
【解答】解:∵xyz<0,
∴x,y,z中负数的个数为1个或3个
∴当x<0,y>0,z>0时
原式=;
当x<0,y<0,z<0时,
原式=;
∴的值为-4或0.
故答案为:-4或0
【分析】利用xyz<0,可知x,y,z中负数的个数为1个或3个,分情况讨论,利用绝对值的性质,可求出结果.
13.-5
【解答】解:∵a+b+c=0,
而a=7,b=﹣2,
∴7+(﹣2)+c=0,即7﹣2+c=0,
∴5+c=0,
∴c=﹣5.
【分析】根据三个数的和为0,即可根据a和b的值求出c的值。
14.9;不能,∵,∴不能用该系统全部识别;
15.-6或4
【解答】若点M向右移动5个单位长度,则点N表示的数为:-1+5=4;
若点M向左移动5个单位长度,则点N表示的数为:-1-5=-6;
综上,点N表示的数是-6或4,
故答案为-6或4.
【分析】由已知条件:点M在数轴上移动5个单位长度后得到点N就是将点M向左或向右平移5个单位,再列式计算。
16.8F
【解答】解:B×D用十进制表示为:11×13,
∵11×13=143,
∵143÷16=8······15,
143用十六进制8F.
故答案为:8F.
【分析】先把B×D用十进制表示,求出这两个数的乘积,然后把结果转化为十六进制表示即可.
17.(1)
(2)
(3)
18.(1)小王在出车地点的西方,距出车地点的距离是25千米;(2)6.09.
19.(1)解: -4+7-2-3-8+8=-2 ,
故小王在下午出车的出发地的北方,距离出发地2km处
(2)解: 8×6+1.8×(4-3)+1.8× (7-3)+1.8×(8-3)×2 =75 (元),
所以小王这天下午收到乘客所给的车费共75元
(3)解:(km),
32×0.1×7=22.4(元),
75 -22.4=52.6(元),
所以小王这天下午赚了52.6元
【分析】 (1)把行车的数据相加,根据和进行判定作答即可;
(2)先计算6次的起步价的全部金额,再找出超过 3km的行车数据,计算超过数量,根据加收金额=1.8超过数量计算即可 ;
(3) 先计算行车数量的绝对值的和,根据 耗油量=0,1行车总量,汽油钱=7 耗油量,用行车收到的费用减去汽油钱即为赚的费用.
20.(1)解: (千米)
答:最后一名老师送到月的地时,小王距出车地点 25 千米。
(2)解: (千米),
(升)
答:这天上午汽车共耗油 34.8 升。
【分析】(1)将题干中的数据相加,再根据结果分析判断即可;
(2)先将题干中的数据的绝对值相加,再利用“总油耗=每千米的油耗×总路程”列出算式求解即可.
21.(1)这6位同学本次竞赛的最高得分是150分
(2)最高分超出最低分80分
(3)这6位同学本次竞赛成绩的总分是618分
22.(1)解:由题意得六班收集废纸的质量最多,超出标准的质量为:(kg),
所以六班收集废纸的质量为(kg).
(2)解:因为六班收集废纸的质量最多,超过标准质量2.5kg,
所以本次活动收集废纸质量排名前三的班级分别为一班、二班、六班.
(kg).
答:获得荣誉称号的班级收集废纸的总质量为20.5kg.
(3)解:(kg),
(元).
答:这些废纸卖出的总钱数为49.5元.
【分析】(1)利用已知“ 收集废纸最多的班级和最少的班级质量差4k ”,可求出超出标准的质量,然后根据各班收集的废纸均以5kg为标准,可求出七年级六班同学收集废纸的质量.
(2)利用表中数据分别计算,然后求出获得荣誉称号的班级收集废纸的总质量.
(3)先列式计算求出总质量,再用总质量×单价,列式计算即可.
23.(1)-5;1
(2)①由于动点P、Q分别同时从A、C出发,分别以每秒8个单位和4个单位的速度沿数轴正方向运动,则AP=8t,CQ=4t,
又 , ,
所以AM=4t,CN=t,
所以点M对应的数为:-5+4t,点N对应的数为:3+t;
②MQ的长度与t无关,为定值8,理由如下:
由于CQ=4t,
所以点Q对应的数为:3+4t,
则MQ=3+4t-(-5+4t)=8;
即MQ的长度与t无关,为定值8;
③因点M对应的数为:-5+4t,点N对应的数为:3+t,
则OM=|-5+4t|,BN=(3+t)-1=t+2,
由于OM=2BN,
所以|-5+4t|=2(t+2),
解得: 或 ;
即当 或 时,OM=2BN.
【解答】解:(1)因为点C对应的数为3,且BC=2,由图知,B点在C的右边,所以点B对应的数为:3-2=1;由AB=6,且点A在原点的左边,所以点A对应的数为:1-6=-5;
故答案为:-5,1;
【分析】(1)根据数轴得知A、B所处的位置,然后由已知条件和数轴上两点间的距离即可求得两点对应的数;
(2)①由路程=速度×时间,根据题意可求得AM、CN的长度,从而由A、C对应的数即可求得M、N对应的数;
②由题意先求出CQ的长,从而得出点Q对应的数,然后再求出MQ的长度是8,它是一个定值,即可作出判断;
③先分别表示出OM、BN的长度,然后根据OM=2BN列出关于t的方程求解即可.
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优浙教版(2024)
第2章 有理数的运算 2.6 有理数的混合运算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若等式2≤(﹣2)=0成立,则“≤”内的运算符号是( ).
A.+ B.﹣ C.× D.÷
2.下列计算正确的是( )
A. B.
C. D.
3.2020年3月抗击“新冠肺炎”居家学习期间,小华计划每天背诵6个汉语成语.将超过的个数记为正数,不足的个数记为负数,某一周连续5天的背诵记录如下:,则这5天他共背诵汉语成语( )
A.8个 B.14个 C.38个 D.36个
4.若a、b互为相反数,x、y互为倒数,则的值是( )
A.3 B.2 C.1 D.5
5.如图,某公园有一长方形广场,长为米,宽为米,在其两角修建半径均为米的扇形花坛,在广场中心修建一个直径为米的圆形喷泉水池,则该广场的空地面积为(取3)( ).
A. B. C. D.
6. 计算 结果是 ( )
A. B. C. D.- 7
7.在遵义拍摄的历史剧《伟大的转折》刚在央视一套热播,为新中国70周年献上了一份大礼.红军行军过程中需要用密码进行信息传输,其中一组密码规定:输入任意一对有理数 (a,b)后就转换得到一个新数a2+b-2,例如输入 (3,-1)就得到32+(-1)-2=6,也就得到了6对应的字.如果输入(-4,7),则得到的对应数字为( )
A.-11 B.21 C.23 D.11
8.用计算器计算时,下列说法错误的是( )
A.“计算 ”的按键顺序是 1 ab/c 2 ﹣ 1 ab/c 3 ab/c 4 =
B.“计算 ”的按键顺序是 3 EXP 5 ﹣ 2 8 =
C.“已知SinA=0.3,求锐角A”的按键顺序是DEL 2ndF sin 0 . 3 =
D.“计算 ”的按键顺序是1 ab/c 2 2ndF 5 =
9.随着2010年元旦的到来, 宁波市各大百货公司纷纷推出各种优惠以答谢顾客, 其中一家百货公司贴出的优惠标语是: 买200元物品, 送100元购物券, 买400元物品送200购物券,……依次类推; 于是小红陪着她的妈妈一起来到百货公司买东西, 没过多少时间小红就看中了一件衣服, 一问价钱需要650元. 她心想贵是贵了点,但是能送300元的购物券还是挺划算的, 于是就花650元把这件衣服买了, 同时也得到了300元购物券. 后来小红又用这310元购物券买了一双鞋子, 这时就没有购物券送了. 则下列优惠中, 与小红在这次购物活动中所享受的优惠最接近的是( )
A.5折 B.6折 C.7折 D.8折
10.规定“!”是一种运算符号,
其中1!=1,
2!=1×2,
3!=1×2×3,
4!=1×2×3×4,…
则 的值为( )
A.2014 B.2015 C.2016 D.2017
二、填空题
11. 10头大象1天的食品可供1000只老鼠吃600天,假定每头大象的食量都一样,每只老鼠的食量也相等,那么m头大象1天的食物可供100只老鼠吃 天.
12.若xyz<0,则 的值为
13.已知有理数a、b、c的和为0,且a=7,b=﹣2,则c= .
14.某校建立了一个身份识别系统,利用如图1(由四个小正方形组成)的条码可以对学生所在班级序号进行识别.黑色小正方形表示1,白色小正方形表示0将数字从左到右依次记为a,b,c,d,则学生的班级序号为(规定).图2是某学生的条码,数字从左到右依次为0,1,0,1,序号为,表示该生为5班的学生.
(1)图3中表示学生所在班级序号是 ;
(2)该校七年级共有18个班,班级序号从1至18,是否能用该系统全部识别?请说明理由: .
15.点M表示的有理数是-1,点M在数轴上移动5个单位长度后得到点N,则点N表示的有理数是 .
16.计算机中常用的十六进制是逢16进1的计数制,采用数字0~9和字母A~F共16个计数符号,这些符号与十进制的数的对应关系如下表:
十六进制 0 1 2 3 4 5 6 7 8 9 A B C D E F
十进制 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
例如,十进制中16+10=26,用十六进制表示为10+A=1A;十进制中25-15=10,用十六进制表示为19 F=A.由上可知,在十六进制中B×D= (运算结果用十六进制表示).
三、计算题
17.计算(其中第(3)题用简便算法)
(1)
(2)
(3)
四、解答题
18.尊老爱幼是我国的传统美德. 九九重阳节这一天上午,出租车司机小王在东西向的公路上免费接送老年人(60周岁以上).如果规定向东为正,向西为负,出租车的行程如下(单位:千米):+15,-4,+13,-10,-12,+3,-13,-17.
⑴将最后一名老人送到目的地时,小王在出发点的什么方向,距离是多少
⑵若出租车耗油量为0.07升/千米,这天上午小王的出租车共耗油多少升
19.出租车司机小王某天下午的一段时间内营运全是在南北走向的北海路上进行的。如果向南记作“+”,向北记作“-”,那么他这段时间内行车情况如下(单位: km。每次行车都有乘客):-4,+7,-2,-3,-8,+8。请解答下列问题:
(1)小王将最后一名乘客送到目的地时,在下午出车的出发地的什么方向 距下午出车的出发地多远
(2)若规定每次乘坐出租车的起步价是8元,且3 km以内(含 3km)只收起步价;若超过3km,除收起步价外,超过的每千米还需收1.8元。小王这段时间内收到乘客所给的车费共多少元
(3)若小王的出租车每千米耗油0.1L,每升汽油7元。不计汽车损耗的情况下,除去汽油钱,请你帮小王计算一下,这段时间内他赚了多少钱
20.上午出租车司机小王在东西向的公路上免费接送老师.如果规定向东为正,向西为负,出租车的行程如下 (单位:千米) :
(1) 最后一名老师送到目的地时,小王距出车地点的距离是多少
(2) 若汽车耗油量为0.4升/千米,这天上午汽车共耗油多少升
21.某校举行了以“珍爱生命、远离水患”为主题的知识竞赛.下表是善思小组6位同学参加此次竞赛的成绩(以100分为标准,超过100分记为“+”,不足100分记为“-”),请根据表中信息解决下列问题.
编号 1 2 3 4 5 6
知识竞赛成绩/分
(1)求这6位同学本次竞赛的最高得分.
(2)最高分超出最低分多少分?
(3)求这6位同学本次竞赛成绩的总分.
22.某校举办了“废纸回收,变废为宝”活动,各班收集的废纸均以5kg为标准,超过的部分记为“+”,不足的部分记为“-”,七年级六个班级的废纸收集情况如下表所示,统计员小虎不小心将一个数据弄脏看不清了,但他记得三班收集的废纸最少,且收集废纸最多的班级和最少的班级质量差4kg.
班级 一 二 三 四 五 六
超过(不足)(kg) +1 +2 -1.5 0 -1
(1)请你计算七年级六班同学收集废纸的质量;
(2)若本次活动收集废纸质量排名前三的班级可获得荣誉称号,请计算获得荣誉称号的班级收集废纸的总质量;
(3)若七年级六个班级将本次活动收集的废纸以1.5元/kg的价格集中卖出,求这些废纸卖出的总钱数.
23.如图,已知点A、B、C是数轴上三点,O为原点.点C对应的数为3,BC=2,AB=6.
(1)则点A对应的数是 、点B对应的数是 ;
(2)动点P、Q分别同时从A、C出发,分别以每秒8个单位和4个单位的速度沿数轴正方向运动.M在线段AP上,且AM=MP,N在线段CQ上,且 ,设运动时间为t(t>0).
①求点M、N对应的数(用含t的式子表示);
②猜想MQ的长度是否与t无关为定值,若为定值请求出该定值,若不为定值请说明理由;
③探究t为何值时,OM=2BN.
参考答案及试题解析
1.A
2.A
3.C
4.A
【解答】解:由题意得:,,
∴.
故选:A.
【分析】根据利用相反数,倒数的定义求出,,代入原式计算求解即可.
5.B
6.C
【解答】解:
.
故答案为:C.
【分析】首先计算第二个括号内的部分,然后将除法转换成乘法并计算即可.
7.B
【解答】解:∵输入(a,b)后,会得到一个新的有理数:a2+b-2,
∴输入(-4,7),得到的结果为:(-4)2+7-2=16+7-2=21,
故答案为:B.
【分析】根据新定义法则列出算式,再根据有理数的加减法法则即可算出答案.
8.D
【解答】解:A、“计算
”的按键顺序是 1 、ab/c 、2 、﹣ 、1 、ab/c 、3、 ab/c、 4 、= 、是正确的,不符题意;
B、“计算
”的按键顺序是 3、 EXP、 5 、﹣、 2 8 、=、是正确的,不符题意;
C、“已知SinA=0.3,求锐角A”的按键顺序是DEL、 2ndF、 sin、 0 . 3、 =、是正确的,不符题意;
D、“计算
”的按键顺序是1 、ab/c 、2 、
、 5、 =、原来的说法是错误的,符合题意;
故答案为:D.
【分析】根据计算器上分数、科学记数法、三角函数及乘方计算方法可得答案.
9.C
【分析】首先计算一下小红实际花了多少钱;650+310-300=660(元),如果不享受优惠则需要花;650+310=960(元),用实际花的钱÷不优惠花的钱,可得到打了几折.
【解答】
实际花钱数÷不优惠花钱数=(650+310-300)÷(650+310)=0.6875≈0.7,
∴小红在这次购物活动中所享受的优惠最接近的是7折.
故选:C.
【点评】此题主要考查了实际生活中的数学问题,解题关键是要读懂题目的意思,找出合适的等量关系.
10.D
【解答】解:根据题中的新定义得:原式= =2017,
故选D
【分析】原式根据题中的新定义化简,计算即可得到结果.
11.600m
【解答】解: m÷100=600m(天).
故答案为:600m.
【分析】根据已知10头大象1天的食品可供1000只老鼠吃600天,假定每头大象的食量都一样,每只老鼠的食量也相等,可求出那么m头大象1天的食品可供100只老鼠吃多少天.
12.-4或0
【解答】解:∵xyz<0,
∴x,y,z中负数的个数为1个或3个
∴当x<0,y>0,z>0时
原式=;
当x<0,y<0,z<0时,
原式=;
∴的值为-4或0.
故答案为:-4或0
【分析】利用xyz<0,可知x,y,z中负数的个数为1个或3个,分情况讨论,利用绝对值的性质,可求出结果.
13.-5
【解答】解:∵a+b+c=0,
而a=7,b=﹣2,
∴7+(﹣2)+c=0,即7﹣2+c=0,
∴5+c=0,
∴c=﹣5.
【分析】根据三个数的和为0,即可根据a和b的值求出c的值。
14.9;不能,∵,∴不能用该系统全部识别;
15.-6或4
【解答】若点M向右移动5个单位长度,则点N表示的数为:-1+5=4;
若点M向左移动5个单位长度,则点N表示的数为:-1-5=-6;
综上,点N表示的数是-6或4,
故答案为-6或4.
【分析】由已知条件:点M在数轴上移动5个单位长度后得到点N就是将点M向左或向右平移5个单位,再列式计算。
16.8F
【解答】解:B×D用十进制表示为:11×13,
∵11×13=143,
∵143÷16=8······15,
143用十六进制8F.
故答案为:8F.
【分析】先把B×D用十进制表示,求出这两个数的乘积,然后把结果转化为十六进制表示即可.
17.(1)
(2)
(3)
18.(1)小王在出车地点的西方,距出车地点的距离是25千米;(2)6.09.
19.(1)解: -4+7-2-3-8+8=-2 ,
故小王在下午出车的出发地的北方,距离出发地2km处
(2)解: 8×6+1.8×(4-3)+1.8× (7-3)+1.8×(8-3)×2 =75 (元),
所以小王这天下午收到乘客所给的车费共75元
(3)解:(km),
32×0.1×7=22.4(元),
75 -22.4=52.6(元),
所以小王这天下午赚了52.6元
【分析】 (1)把行车的数据相加,根据和进行判定作答即可;
(2)先计算6次的起步价的全部金额,再找出超过 3km的行车数据,计算超过数量,根据加收金额=1.8超过数量计算即可 ;
(3) 先计算行车数量的绝对值的和,根据 耗油量=0,1行车总量,汽油钱=7 耗油量,用行车收到的费用减去汽油钱即为赚的费用.
20.(1)解: (千米)
答:最后一名老师送到月的地时,小王距出车地点 25 千米。
(2)解: (千米),
(升)
答:这天上午汽车共耗油 34.8 升。
【分析】(1)将题干中的数据相加,再根据结果分析判断即可;
(2)先将题干中的数据的绝对值相加,再利用“总油耗=每千米的油耗×总路程”列出算式求解即可.
21.(1)这6位同学本次竞赛的最高得分是150分
(2)最高分超出最低分80分
(3)这6位同学本次竞赛成绩的总分是618分
22.(1)解:由题意得六班收集废纸的质量最多,超出标准的质量为:(kg),
所以六班收集废纸的质量为(kg).
(2)解:因为六班收集废纸的质量最多,超过标准质量2.5kg,
所以本次活动收集废纸质量排名前三的班级分别为一班、二班、六班.
(kg).
答:获得荣誉称号的班级收集废纸的总质量为20.5kg.
(3)解:(kg),
(元).
答:这些废纸卖出的总钱数为49.5元.
【分析】(1)利用已知“ 收集废纸最多的班级和最少的班级质量差4k ”,可求出超出标准的质量,然后根据各班收集的废纸均以5kg为标准,可求出七年级六班同学收集废纸的质量.
(2)利用表中数据分别计算,然后求出获得荣誉称号的班级收集废纸的总质量.
(3)先列式计算求出总质量,再用总质量×单价,列式计算即可.
23.(1)-5;1
(2)①由于动点P、Q分别同时从A、C出发,分别以每秒8个单位和4个单位的速度沿数轴正方向运动,则AP=8t,CQ=4t,
又 , ,
所以AM=4t,CN=t,
所以点M对应的数为:-5+4t,点N对应的数为:3+t;
②MQ的长度与t无关,为定值8,理由如下:
由于CQ=4t,
所以点Q对应的数为:3+4t,
则MQ=3+4t-(-5+4t)=8;
即MQ的长度与t无关,为定值8;
③因点M对应的数为:-5+4t,点N对应的数为:3+t,
则OM=|-5+4t|,BN=(3+t)-1=t+2,
由于OM=2BN,
所以|-5+4t|=2(t+2),
解得: 或 ;
即当 或 时,OM=2BN.
【解答】解:(1)因为点C对应的数为3,且BC=2,由图知,B点在C的右边,所以点B对应的数为:3-2=1;由AB=6,且点A在原点的左边,所以点A对应的数为:1-6=-5;
故答案为:-5,1;
【分析】(1)根据数轴得知A、B所处的位置,然后由已知条件和数轴上两点间的距离即可求得两点对应的数;
(2)①由路程=速度×时间,根据题意可求得AM、CN的长度,从而由A、C对应的数即可求得M、N对应的数;
②由题意先求出CQ的长,从而得出点Q对应的数,然后再求出MQ的长度是8,它是一个定值,即可作出判断;
③先分别表示出OM、BN的长度,然后根据OM=2BN列出关于t的方程求解即可.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
