【章节考点培优】3.4实数的运算-2025-2026学年七年级上册数学浙教版(2024)(含答案解析)
文档属性
| 名称 | 【章节考点培优】3.4实数的运算-2025-2026学年七年级上册数学浙教版(2024)(含答案解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 199.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 00:00:00 | ||
图片预览




文档简介
/ 让学习更有效 新课备课备考 | 数学学科
2025-2026学年七年级上册数学单元考点培优浙教版(2024)
第2章 实数 3.4 实数的运算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列长度的三条线段能组成直角三角形的是( )
A.,, B.,, C.,, D.,,
2.下列式子运算正确的是( )
A.a2+a3=a5 B.a8÷a2=a6
C.(a+1)0+()﹣1=﹣1 D. +=0
3.要使算式□的运算结果最大,则“□”内应填入的运算符号为( )
A. B. C. D.
4.比实数3 的相反数小7的数是( )
A.3 +7 B.3 -7 C.-3 +7 D.-3 -7
5.计算(-2)2019+22018的结果是( )
A.-22018 B.22018 C.22019 D.-2
6.计算:( )﹣1+tan30° sin60°=( )
A.﹣ B.2 C. D.
7.估计 的值在( )
A.3和3.5之间 B.2.5和3之间 C.2和2.5之间 D.1.5和2之间
8.下列计算正确的是( )
A.-= B.×=6 C.+=5 D.÷=4
9.计算的结果,正确的是( )
A. B. C. D.
10.我们定义一种新运算ab(a,b是实数),规定:ab=a2﹣ab﹣10b,等式右边是正常的实数运算,若x2=4,则x的值为( )
A.6或﹣4 B.﹣6或4 C.1+或1﹣ D.5或﹣4
二、填空题
11.计算: =
12.计算: = .
13.计算:﹣22+()﹣1+=
14.用“ ”定义新运算:对于任意实数a,b,都有 .例如: ,那么2022 5= ;当m为实数时, = .
15.在实数范围内因式分解: .
16.设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是 .①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是1;④存在实数x,使[x)-x=0.5成立.
三、计算题
17.(1)计算:.
(2)化简:.
四、解答题
18.计算:
(1)(﹣5)0﹣()2+|﹣3|; (2)(x+1)2﹣2(x﹣2).
19.为推进乡村振兴,把家乡建设成为生态宜居、交通便利的美丽家园,某地大力修建崭新的公路.如图,现从A地分别向C、D、B三地修了三条笔直的公路、和,C地、D地、B地在同一笔直公路上,公路和公路互相垂直,又从D地修了一条笔直的公路与公路在H处连接,且公路和公路互相垂直,已知千米,千米,千米.
(1)求公路、的长度;
(2)若修公路每千米的费用是2000万元,请求出修建公路的费用.
20.先阅读下面的文字,然后解答问题.
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用表示的小数部分,你同意小明的表示方法吗 事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
由此我们还可以得到一个真命题:如果,其中是整数,且,那么,.请解答下列问题:
(1)如果,其中a是整数,且,那么 ,b= ;
(2)已知,其中m是整数,且,求的值;
(3)的整数部分是 ,小数部分是 .
21.计算:(﹣1)2011+2tan60°+20﹣+|1﹣|.
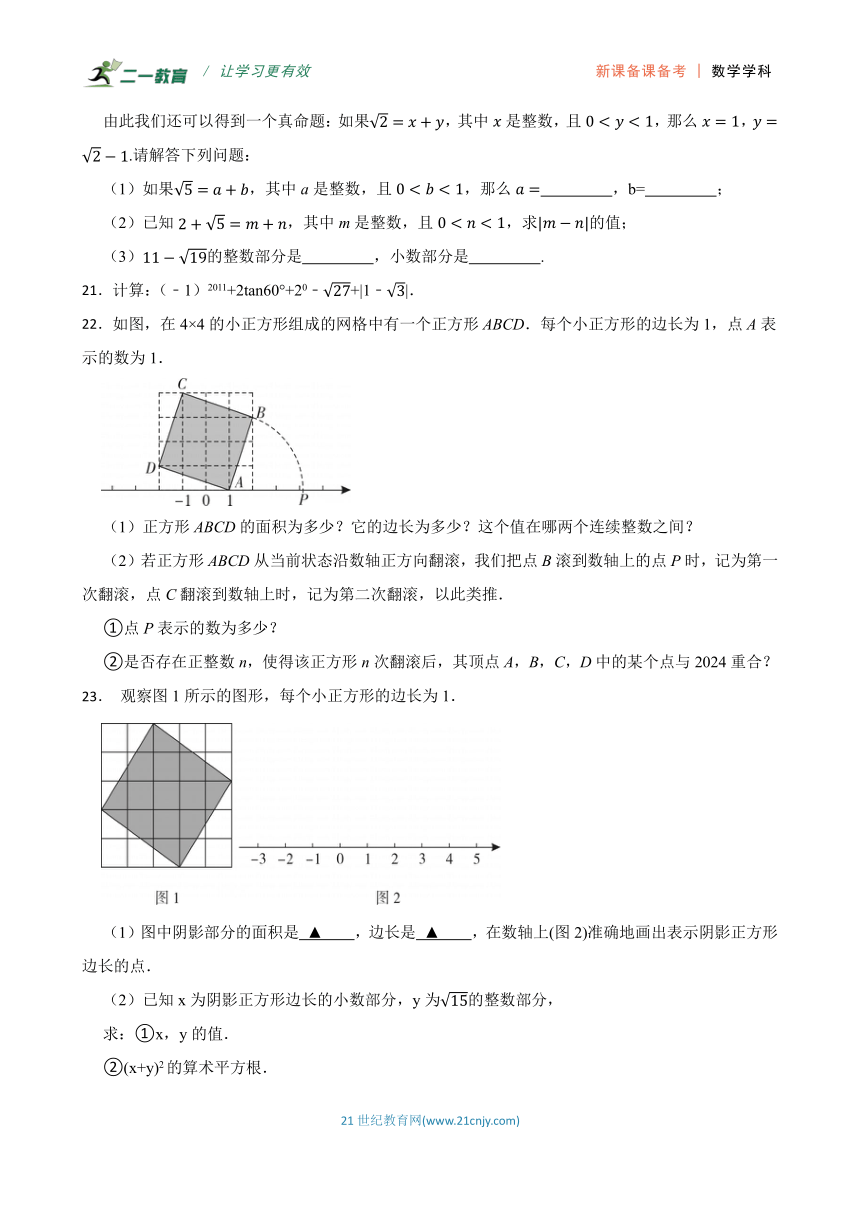
22.如图,在4×4的小正方形组成的网格中有一个正方形ABCD.每个小正方形的边长为1,点A表示的数为1.
(1)正方形ABCD的面积为多少?它的边长为多少?这个值在哪两个连续整数之间?
(2)若正方形ABCD从当前状态沿数轴正方向翻滚,我们把点B滚到数轴上的点P时,记为第一次翻滚,点C翻滚到数轴上时,记为第二次翻滚,以此类推.
①点P表示的数为多少?
②是否存在正整数n,使得该正方形n次翻滚后,其顶点A,B,C,D中的某个点与2024重合?
23. 观察图1所示的图形,每个小正方形的边长为1.
(1)图中阴影部分的面积是 ▲ ,边长是 ▲ ,在数轴上(图2)准确地画出表示阴影正方形边长的点.
(2)已知x为阴影正方形边长的小数部分,y为的整数部分,
求:①x,y的值.
②(x+y)2的算术平方根.
参考答案及试题解析
1.【答案】D
【解析】【解答】解:A、,故A不符合题意;
B、 ,故B不符合题意;
C、,故C不符合题意;
D、 ,故D符合题意;
故答案为:D.
【分析】
根据勾股定理逆定理 :如果一个三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形;逐项分析即可求解.
2.【答案】B
【解析】【解答】解:A.∵a2与a3不是同类项,不能合并,∴选项A不符合题意;
B.∵a8÷a2=a6,∴选项B符合题意;
C.∵(a+1)0+()﹣1=1+2=3,∴选项C不符合题意;
D.∵+=2﹣2≠0,∴选项D不符合题意.
故答案为:B.
【分析】根据合并同类项、同底数幂的除法、幂的乘方的运算、算术平方根及立方根分别计算,再判断即可.
3.【答案】A
【解析】【解答】解:A、
B、
C、
D、
∵
故答案为:A.
【分析】根据有理数的计算法则,逐项计算进而比较即可.
4.【答案】D
【解析】【解答】解:∵实数3 的相反数是:-3 ,
∴比实数3 的相反数小7的数是: -3 -7.
故答案为:D.
【分析】先求出实数3 的相反数,再求出比实数3 的相反数小7的数即是:-3 和7的差.
5.【答案】A
【解析】【解答】(-2)2019+22018=(-2)×22018+22018=22018×(-2+1)=-22018
故答案为:A
【分析】逆用同底数幂相乘底数不变指数相加,把(-2)2019变形为(-2)×22018,再利用提公因式法即可求出答案.
6.【答案】C
【解析】【解答】( )﹣1+tan30° sin60°
=2+
=2+
= ,
故答案为:C.
【分析】根据负指数的意义,特殊锐角三角函数值,分别化简,再根据实数的运算法则,算出答案。
7.【答案】A
【解析】【解答】解:
=2+
= ;
∵4<5<6.25,
∴2< <2.5,
∴3< <3.5,
即 的值在3和3.5之间.
故答案为:A.
【分析】先利用二次根式混合运算求解,再估算大小即可。
8.【答案】A
【解析】【解答】解:A、原式=2﹣=,正确;
B、原式==,错误;
C、+为最简结果,错误;
D、原式==2,错误,
故选A
【分析】原式各项化简得到结果,即可做出判断.
9.【答案】B
【解析】【解答】解:
=
=
=.
故答案为:B.
【分析】根据二次根式的性质、绝对值的性质以及特殊角的三角函数值分别化简,然后计算乘法,再合并同类二次根式即可.
10.【答案】A
【解析】【解答】解:∵ab=a2﹣ab﹣10b,
∴x2=x2﹣2x﹣20=4,解得x1=﹣4,x2=6.
故选A.
【分析】先根据题意列出关于x的方程,求出x的值即可.
11.【答案】-10
【解析】【解答】解:原式=-3-7=-10.
故答案为:-10.
【分析】先进行平方根和立方根的化简,再进行有理数的减法运算,即得结果.
12.【答案】
【解析】【解答】解:
=
= ;
故答案为: .
【分析】根据绝对值,二次根式的性质,算术平方根进行化简,即可得到答案.
13.【答案】-3
【解析】【解答】解:原式=﹣4+2+﹣1=﹣3,
故答案为: ﹣3
【分析】原式第一项利用乘方的意义计算,第二项利用负整数指数幂法则计算,最后一项利用二次根式性质计算即可得到结果.
14.【答案】26;26
【解析】【解答】解:20225=52+1=26;
m(m2)=m(22+1)=52+1=26.
故答案为:26;26.
【分析】根据定义运算:ab=b2+1,分别代入数据进行计算,即可求解.
15.【答案】
16.【答案】③④
【解析】【解答】解:①[0)=1,故本项错误;②[x)-x>0,但是取不到0,故本项错误;③[x)-x≤1,即最大值为1,故本项正确;④存在实数x,使[x)-x=0.5成立,例如x=0.5时,故本项正确.
故答案为③④.
【分析】关于实数的新定义问题,根据定义进行判断即可。
17.【答案】(1)解:,
,
;
(2)解:,
,
.
【解析】【分析】本题考查了二次根式性质、绝对值化简、零指数幂以及整式的混合运算运算等知识,解题的关键是掌握运算的顺序和相关运算的法则.
(1)根据二次根式性质、任何不为0的数的0次幂都等于1和负数的绝对值是其相反数的计算法则化简每一项,再进行加减混合运算即可;
(2)利用两个数的和与这两个数的差相乘,等于这两个数的平方差,单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加,再进行合并同类项计算即可.
18.【答案】解:(1)原式=1﹣3+3=1.(2)原式=x2+2x+1﹣2x+4=x2+5.
【解析】【解答】(1)原式=1﹣3+3=1.(2)原式=x2+2x+1﹣2x+4=x2+5.
【分析】(1)先算0指数幂、平方和绝对值,再算加减;(2)利用完全平方公式计算,再合并得出答案即可.
19.【答案】(1)解:∵,千米,千米,
∴千米,
∵千米,
∴千米,
∴千米;
(2)解:∵,
∴,
∵BD=5千米,AC=9千米,AB=15千米,
∴千米,
∴修建公路的费用为(万元).
【解析】【分析】(1)根据勾股定理得出千米,再求出千米,然后根据勾股定理即可得出答案;
(2)根据面积相等得,代入数据,即可得出答案.
20.【答案】(1)2;
(2)解:根据题意得
∵,∴.
∴的整数部分为2+2=4.∴.
∵,∴.
∴把,代入.
.
(3)6;
【解析】【解答】解:(1)∵2<<3,且,其中a是整数,且
∴a=2,b=-2.
故答案为:2,-2.
(3)∵4<<5,
∴-5<-<-4,
∴11-5<11-<11-4,即6<11-<7,
∴的整数部分是6, 小数部分是-6= .
故答案为:6,.
【分析】(1)根据夹逼法知:2<<3,据此解答即可;
(2)根据夹逼法知2<<3,从而得出4<2+<5,就确定m、n的值,再将七代人计算即可;
(3)由4<<5可得-5<-<-4,继而得出11-5<11-<11-4,据此即可求解.
21.【答案】解:原式=﹣1+2+1﹣3+﹣1
=﹣1.
【解析】【分析】根据零指数幂、乘方、特殊角的三角函数值以及绝对值进行计算即可.
22.【答案】(1)解:则正方形ABCD的面积;它的边长为;在3和4之间.
(2)①点P表示的数为1+;
②由题意,n+1=2024,整理,得=-,∵n是正整数,∴左边是无理数,右边是有理数,∴不存在正整数n,使得该正方形n次翻滚后,其顶点A,B,C,D中的某个点与2024重合.
【解析】【分析】(1)、由图可以看出,正方形ABCD与非阴影区的4个相等的直角三角形共同构成了外围的大正方形,只需用大正方形的面积减去4个直角三角形的面积及可求出;求的算术平方根即可求出边长为;因为32<10<42,所以,即介乎3和4这两个整数之间;(2)、①由图可知,为,则P所表示的数为+1;②滚动1次后B落于数轴,从此时开始继续滚动,C、D、A、B、C……循环落于数轴,每滚动1次,新落于数轴的点所表示的数比上一次落于数轴的点所表示的数大,n次后即为n+1. 不难看出,n是正整数的前提下,n+1不可能等于一个正整数,也就不可能等于2024.
23.【答案】(1)13;
如图,点P即为表示的点.
(2)①∵3<<4,
∴的小数部分为-3,
即x=-3.
又∵3<<4,
的整数部分是3,
即y=3.
②当x=-3,y=3时,
(x+y)2=(-3+3)2=13.
所以(x+y)2的算术平方根为.
【解析】【解答】解:(1)),
边长.
故答案为:13;;
【分析】(1)先利用割补法计算出阴影部分面积,再根据正方形的性质求得边长,然后通过勾股定理在数轴上表示出点P;
(2)①被开方数的值越大,对应的算术平方根的值也越大,找到与被开方数相邻近的平方数是解题关键,从而确定的取值范围,得到x、y的值;
②代入x、y的值,求得(x+y)2的算术平方根.
21世纪教育网(www.21cnjy.com)
2025-2026学年七年级上册数学单元考点培优浙教版(2024)
第2章 实数 3.4 实数的运算
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列长度的三条线段能组成直角三角形的是( )
A.,, B.,, C.,, D.,,
2.下列式子运算正确的是( )
A.a2+a3=a5 B.a8÷a2=a6
C.(a+1)0+()﹣1=﹣1 D. +=0
3.要使算式□的运算结果最大,则“□”内应填入的运算符号为( )
A. B. C. D.
4.比实数3 的相反数小7的数是( )
A.3 +7 B.3 -7 C.-3 +7 D.-3 -7
5.计算(-2)2019+22018的结果是( )
A.-22018 B.22018 C.22019 D.-2
6.计算:( )﹣1+tan30° sin60°=( )
A.﹣ B.2 C. D.
7.估计 的值在( )
A.3和3.5之间 B.2.5和3之间 C.2和2.5之间 D.1.5和2之间
8.下列计算正确的是( )
A.-= B.×=6 C.+=5 D.÷=4
9.计算的结果,正确的是( )
A. B. C. D.
10.我们定义一种新运算ab(a,b是实数),规定:ab=a2﹣ab﹣10b,等式右边是正常的实数运算,若x2=4,则x的值为( )
A.6或﹣4 B.﹣6或4 C.1+或1﹣ D.5或﹣4
二、填空题
11.计算: =
12.计算: = .
13.计算:﹣22+()﹣1+=
14.用“ ”定义新运算:对于任意实数a,b,都有 .例如: ,那么2022 5= ;当m为实数时, = .
15.在实数范围内因式分解: .
16.设[x)表示大于x的最小整数,如[3)=4,[-1.2)=-1,则下列结论中正确的是 .①[0)=0;②[x)-x的最小值是0;③[x)-x的最大值是1;④存在实数x,使[x)-x=0.5成立.
三、计算题
17.(1)计算:.
(2)化简:.
四、解答题
18.计算:
(1)(﹣5)0﹣()2+|﹣3|; (2)(x+1)2﹣2(x﹣2).
19.为推进乡村振兴,把家乡建设成为生态宜居、交通便利的美丽家园,某地大力修建崭新的公路.如图,现从A地分别向C、D、B三地修了三条笔直的公路、和,C地、D地、B地在同一笔直公路上,公路和公路互相垂直,又从D地修了一条笔直的公路与公路在H处连接,且公路和公路互相垂直,已知千米,千米,千米.
(1)求公路、的长度;
(2)若修公路每千米的费用是2000万元,请求出修建公路的费用.
20.先阅读下面的文字,然后解答问题.
大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用表示的小数部分,你同意小明的表示方法吗 事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
由此我们还可以得到一个真命题:如果,其中是整数,且,那么,.请解答下列问题:
(1)如果,其中a是整数,且,那么 ,b= ;
(2)已知,其中m是整数,且,求的值;
(3)的整数部分是 ,小数部分是 .
21.计算:(﹣1)2011+2tan60°+20﹣+|1﹣|.
22.如图,在4×4的小正方形组成的网格中有一个正方形ABCD.每个小正方形的边长为1,点A表示的数为1.
(1)正方形ABCD的面积为多少?它的边长为多少?这个值在哪两个连续整数之间?
(2)若正方形ABCD从当前状态沿数轴正方向翻滚,我们把点B滚到数轴上的点P时,记为第一次翻滚,点C翻滚到数轴上时,记为第二次翻滚,以此类推.
①点P表示的数为多少?
②是否存在正整数n,使得该正方形n次翻滚后,其顶点A,B,C,D中的某个点与2024重合?
23. 观察图1所示的图形,每个小正方形的边长为1.
(1)图中阴影部分的面积是 ▲ ,边长是 ▲ ,在数轴上(图2)准确地画出表示阴影正方形边长的点.
(2)已知x为阴影正方形边长的小数部分,y为的整数部分,
求:①x,y的值.
②(x+y)2的算术平方根.
参考答案及试题解析
1.【答案】D
【解析】【解答】解:A、,故A不符合题意;
B、 ,故B不符合题意;
C、,故C不符合题意;
D、 ,故D符合题意;
故答案为:D.
【分析】
根据勾股定理逆定理 :如果一个三角形的三边a,b,c满足a2+b2=c2,则这个三角形是直角三角形;逐项分析即可求解.
2.【答案】B
【解析】【解答】解:A.∵a2与a3不是同类项,不能合并,∴选项A不符合题意;
B.∵a8÷a2=a6,∴选项B符合题意;
C.∵(a+1)0+()﹣1=1+2=3,∴选项C不符合题意;
D.∵+=2﹣2≠0,∴选项D不符合题意.
故答案为:B.
【分析】根据合并同类项、同底数幂的除法、幂的乘方的运算、算术平方根及立方根分别计算,再判断即可.
3.【答案】A
【解析】【解答】解:A、
B、
C、
D、
∵
故答案为:A.
【分析】根据有理数的计算法则,逐项计算进而比较即可.
4.【答案】D
【解析】【解答】解:∵实数3 的相反数是:-3 ,
∴比实数3 的相反数小7的数是: -3 -7.
故答案为:D.
【分析】先求出实数3 的相反数,再求出比实数3 的相反数小7的数即是:-3 和7的差.
5.【答案】A
【解析】【解答】(-2)2019+22018=(-2)×22018+22018=22018×(-2+1)=-22018
故答案为:A
【分析】逆用同底数幂相乘底数不变指数相加,把(-2)2019变形为(-2)×22018,再利用提公因式法即可求出答案.
6.【答案】C
【解析】【解答】( )﹣1+tan30° sin60°
=2+
=2+
= ,
故答案为:C.
【分析】根据负指数的意义,特殊锐角三角函数值,分别化简,再根据实数的运算法则,算出答案。
7.【答案】A
【解析】【解答】解:
=2+
= ;
∵4<5<6.25,
∴2< <2.5,
∴3< <3.5,
即 的值在3和3.5之间.
故答案为:A.
【分析】先利用二次根式混合运算求解,再估算大小即可。
8.【答案】A
【解析】【解答】解:A、原式=2﹣=,正确;
B、原式==,错误;
C、+为最简结果,错误;
D、原式==2,错误,
故选A
【分析】原式各项化简得到结果,即可做出判断.
9.【答案】B
【解析】【解答】解:
=
=
=.
故答案为:B.
【分析】根据二次根式的性质、绝对值的性质以及特殊角的三角函数值分别化简,然后计算乘法,再合并同类二次根式即可.
10.【答案】A
【解析】【解答】解:∵ab=a2﹣ab﹣10b,
∴x2=x2﹣2x﹣20=4,解得x1=﹣4,x2=6.
故选A.
【分析】先根据题意列出关于x的方程,求出x的值即可.
11.【答案】-10
【解析】【解答】解:原式=-3-7=-10.
故答案为:-10.
【分析】先进行平方根和立方根的化简,再进行有理数的减法运算,即得结果.
12.【答案】
【解析】【解答】解:
=
= ;
故答案为: .
【分析】根据绝对值,二次根式的性质,算术平方根进行化简,即可得到答案.
13.【答案】-3
【解析】【解答】解:原式=﹣4+2+﹣1=﹣3,
故答案为: ﹣3
【分析】原式第一项利用乘方的意义计算,第二项利用负整数指数幂法则计算,最后一项利用二次根式性质计算即可得到结果.
14.【答案】26;26
【解析】【解答】解:20225=52+1=26;
m(m2)=m(22+1)=52+1=26.
故答案为:26;26.
【分析】根据定义运算:ab=b2+1,分别代入数据进行计算,即可求解.
15.【答案】
16.【答案】③④
【解析】【解答】解:①[0)=1,故本项错误;②[x)-x>0,但是取不到0,故本项错误;③[x)-x≤1,即最大值为1,故本项正确;④存在实数x,使[x)-x=0.5成立,例如x=0.5时,故本项正确.
故答案为③④.
【分析】关于实数的新定义问题,根据定义进行判断即可。
17.【答案】(1)解:,
,
;
(2)解:,
,
.
【解析】【分析】本题考查了二次根式性质、绝对值化简、零指数幂以及整式的混合运算运算等知识,解题的关键是掌握运算的顺序和相关运算的法则.
(1)根据二次根式性质、任何不为0的数的0次幂都等于1和负数的绝对值是其相反数的计算法则化简每一项,再进行加减混合运算即可;
(2)利用两个数的和与这两个数的差相乘,等于这两个数的平方差,单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加,再进行合并同类项计算即可.
18.【答案】解:(1)原式=1﹣3+3=1.(2)原式=x2+2x+1﹣2x+4=x2+5.
【解析】【解答】(1)原式=1﹣3+3=1.(2)原式=x2+2x+1﹣2x+4=x2+5.
【分析】(1)先算0指数幂、平方和绝对值,再算加减;(2)利用完全平方公式计算,再合并得出答案即可.
19.【答案】(1)解:∵,千米,千米,
∴千米,
∵千米,
∴千米,
∴千米;
(2)解:∵,
∴,
∵BD=5千米,AC=9千米,AB=15千米,
∴千米,
∴修建公路的费用为(万元).
【解析】【分析】(1)根据勾股定理得出千米,再求出千米,然后根据勾股定理即可得出答案;
(2)根据面积相等得,代入数据,即可得出答案.
20.【答案】(1)2;
(2)解:根据题意得
∵,∴.
∴的整数部分为2+2=4.∴.
∵,∴.
∴把,代入.
.
(3)6;
【解析】【解答】解:(1)∵2<<3,且,其中a是整数,且
∴a=2,b=-2.
故答案为:2,-2.
(3)∵4<<5,
∴-5<-<-4,
∴11-5<11-<11-4,即6<11-<7,
∴的整数部分是6, 小数部分是-6= .
故答案为:6,.
【分析】(1)根据夹逼法知:2<<3,据此解答即可;
(2)根据夹逼法知2<<3,从而得出4<2+<5,就确定m、n的值,再将七代人计算即可;
(3)由4<<5可得-5<-<-4,继而得出11-5<11-<11-4,据此即可求解.
21.【答案】解:原式=﹣1+2+1﹣3+﹣1
=﹣1.
【解析】【分析】根据零指数幂、乘方、特殊角的三角函数值以及绝对值进行计算即可.
22.【答案】(1)解:则正方形ABCD的面积;它的边长为;在3和4之间.
(2)①点P表示的数为1+;
②由题意,n+1=2024,整理,得=-,∵n是正整数,∴左边是无理数,右边是有理数,∴不存在正整数n,使得该正方形n次翻滚后,其顶点A,B,C,D中的某个点与2024重合.
【解析】【分析】(1)、由图可以看出,正方形ABCD与非阴影区的4个相等的直角三角形共同构成了外围的大正方形,只需用大正方形的面积减去4个直角三角形的面积及可求出;求的算术平方根即可求出边长为;因为32<10<42,所以,即介乎3和4这两个整数之间;(2)、①由图可知,为,则P所表示的数为+1;②滚动1次后B落于数轴,从此时开始继续滚动,C、D、A、B、C……循环落于数轴,每滚动1次,新落于数轴的点所表示的数比上一次落于数轴的点所表示的数大,n次后即为n+1. 不难看出,n是正整数的前提下,n+1不可能等于一个正整数,也就不可能等于2024.
23.【答案】(1)13;
如图,点P即为表示的点.
(2)①∵3<<4,
∴的小数部分为-3,
即x=-3.
又∵3<<4,
的整数部分是3,
即y=3.
②当x=-3,y=3时,
(x+y)2=(-3+3)2=13.
所以(x+y)2的算术平方根为.
【解析】【解答】解:(1)),
边长.
故答案为:13;;
【分析】(1)先利用割补法计算出阴影部分面积,再根据正方形的性质求得边长,然后通过勾股定理在数轴上表示出点P;
(2)①被开方数的值越大,对应的算术平方根的值也越大,找到与被开方数相邻近的平方数是解题关键,从而确定的取值范围,得到x、y的值;
②代入x、y的值,求得(x+y)2的算术平方根.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
