2.6 有理数的混合运算 同步练习(含答案)
文档属性
| 名称 | 2.6 有理数的混合运算 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 315.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-23 15:56:34 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2.6 有理数的混合运算
一、单选题
1.(2023七上·平泉期末)计算:( ).
A.0 B. C. D.
2.现规定一种新运算“※”:a※ 如 则 ※ 的值为 ( )
A.4 B.3 C.1 D.-1
3.(2024七上·西山月考)在数学课上,老师让甲、乙、丙、丁四位同学分别做了一道有理数运算题,你认为做对的同学是( )
甲:;
乙:;
丙:;
丁:.
A.甲 B.乙 C.丙 D.丁
4.(2024·和平模拟)计算的结果等于( )
A. B. C. D.
5.(2024七上·韶山月考)计算:( )
A. B. C.0 D.2
6.在计算器的键盘中,表示开启电源的键是( )
A.OFF B.AC/ON C.MODE D.SHIFT
7.把(﹣8)﹣(+4)+(﹣5)﹣(﹣2)写成省略加号的形式是( )
A.﹣8+4﹣5+2 B.﹣8﹣4﹣5+2
C.﹣8﹣4+5+2 D.8﹣4﹣5+2
8.(2020七上·怀宁期末)下列运算中正确的是( ).
A.8-(-2)=8+2 B.(-5)÷( )=-5×2
C.(-3)×(-4)=-7 D.2-7=(+2)+(+7)
9.若|x|=3,y2=4,且x+y<0,则xy的值为( )
A.6 B.±6 C.-6 D.3
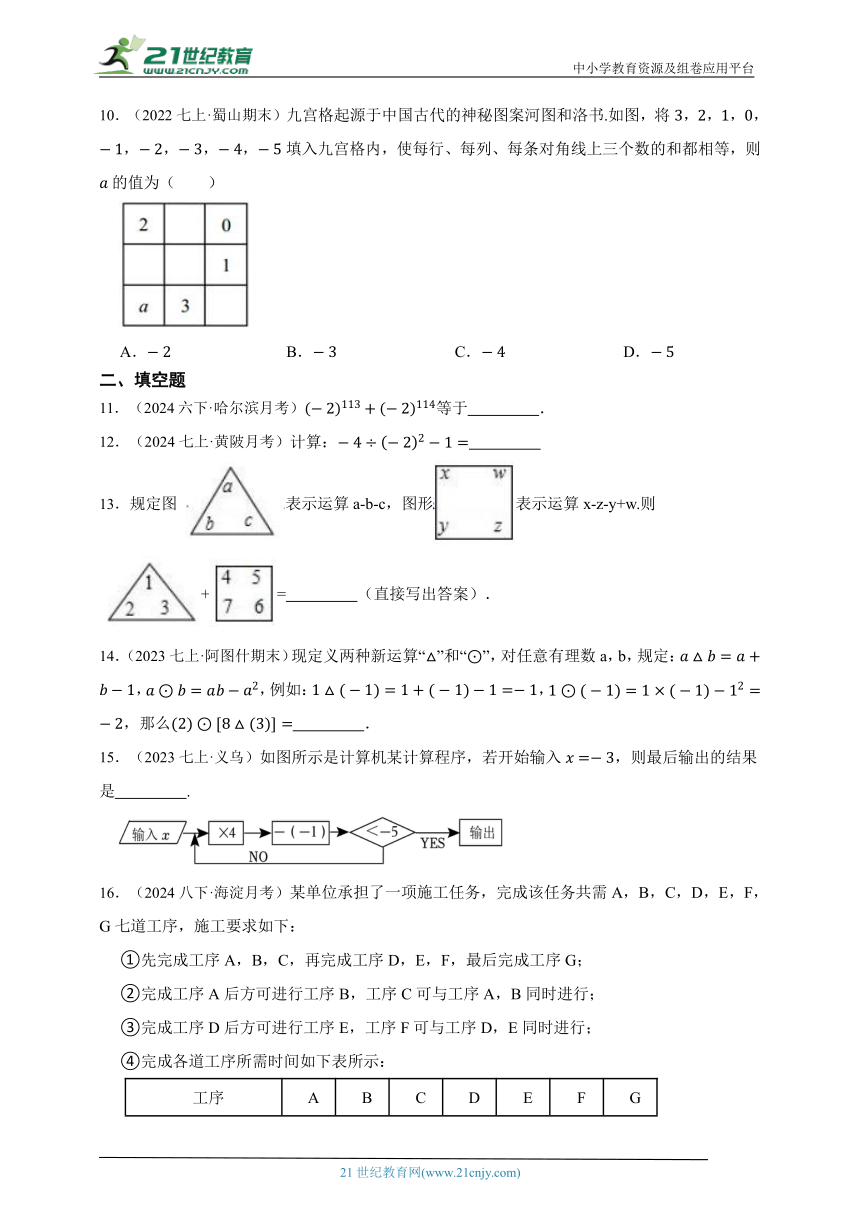
10.(2022七上·蜀山期末)九宫格起源于中国古代的神秘图案河图和洛书.如图,将,,,,,,,,填入九宫格内,使每行、每列、每条对角线上三个数的和都相等,则的值为( )
A. B. C. D.
二、填空题
11.(2024六下·哈尔滨月考)等于 .
12.(2024七上·黄陂月考)计算:
13.规定图表示运算a-b-c,图形表示运算x-z-y+w.则+= (直接写出答案).
14.(2023七上·阿图什期末)现定义两种新运算“”和“”,对任意有理数a,b,规定:,,例如:,,那么 .
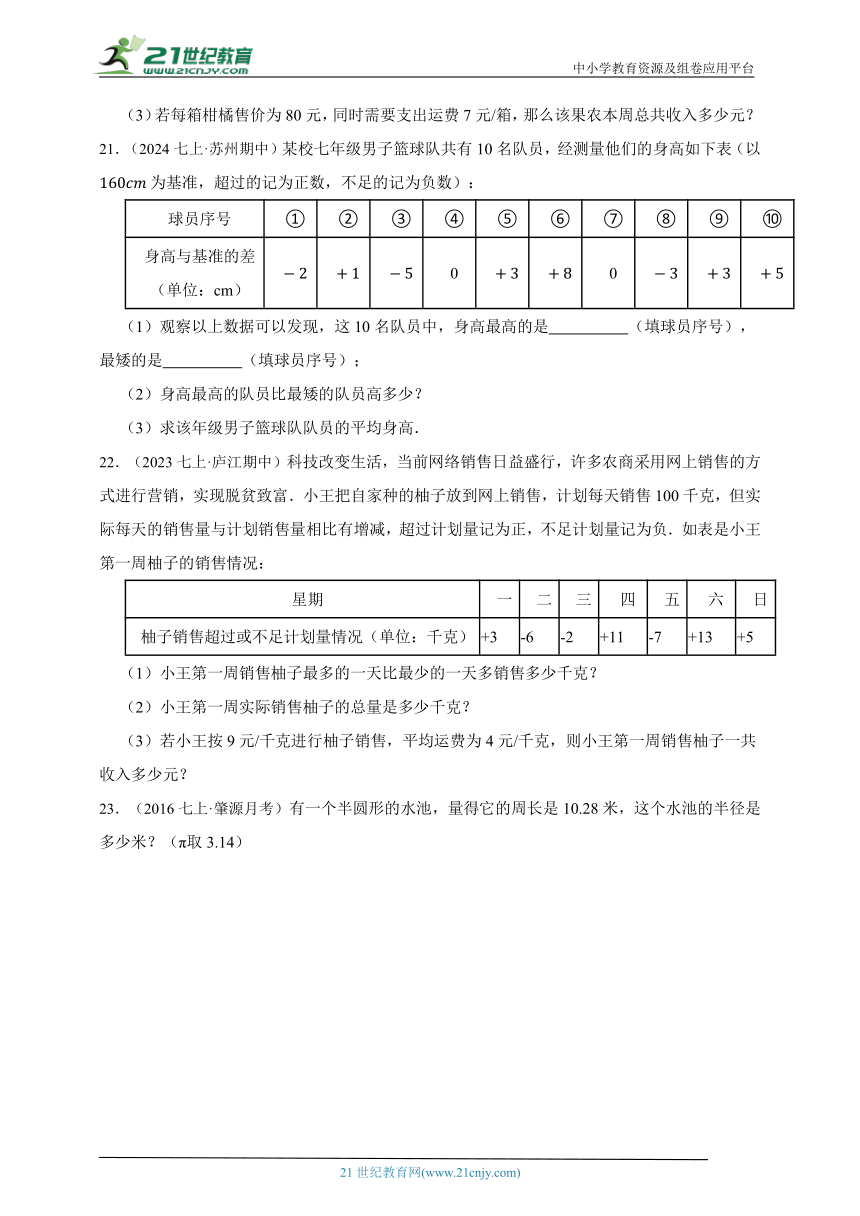
15.(2023七上·义乌)如图所示是计算机某计算程序,若开始输入,则最后输出的结果是 .
16.(2024八下·海淀月考)某单位承担了一项施工任务,完成该任务共需A,B,C,D,E,F,G七道工序,施工要求如下:
①先完成工序A,B,C,再完成工序D,E,F,最后完成工序G;
②完成工序A后方可进行工序B,工序C可与工序A,B同时进行;
③完成工序D后方可进行工序E,工序F可与工序D,E同时进行;
④完成各道工序所需时间如下表所示:
工序 A B C D E F G
所需时间/天 11 15 28 17 16 31 25
(1)在不考虑其它因素的前提下,该施工任务最少 天完成;
(2)现因情况有变,需将工期缩短到80天,工序A,C,D每缩短1天需增加的投入分别为5万元,4万元,6万元,其余工序所需时间不可缩短,则所增加的投入最少是 万元.
三、计算题
17.(2024七上·苏州期中)计算:
(1)
(2)
(3)
(4)
18.(2022七上·博白期末)计算:
(1)
(2)
19.(2024七上·成都期中)观察下列式子:
将以上三个等式两边分别相加得:
.
(1)直接写出结果:_______;
(2)请用上述方法计算(写出具体过程):______;;
(3)直接写出计算结果:_______;
(4)直接写出计算结果:________;
四、解答题
20.(2023七上·吴兴期中)某果农把自家果园的柑橘包装后放到了网上销售.原计划每天卖10箱,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某个星期的销售情况(超额记为正,不足记为负,单位:箱).
星期 一 二 三 四 五 六 日
与计划量的差值 +4 ﹣3 ﹣5 +7 ﹣8 +21 ﹣6
(1)根据记录的数据可知前五天共卖出多少箱?
(2)本周实际销售总量达到了计划数量没有?
(3)若每箱柑橘售价为80元,同时需要支出运费7元/箱,那么该果农本周总共收入多少元?
21.(2024七上·苏州期中)某校七年级男子篮球队共有10名队员,经测量他们的身高如下表(以为基准,超过的记为正数,不足的记为负数):
球员序号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
身高与基准的差 (单位:cm) 0 0
(1)观察以上数据可以发现,这10名队员中,身高最高的是 (填球员序号),最矮的是 (填球员序号);
(2)身高最高的队员比最矮的队员高多少?
(3)求该年级男子篮球队队员的平均身高.
22.(2023七上·庐江期中)科技改变生活,当前网络销售日益盛行,许多农商采用网上销售的方式进行营销,实现脱贫致富.小王把自家种的柚子放到网上销售,计划每天销售100千克,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负.如表是小王第一周柚子的销售情况:
星期 一 二 三 四 五 六 日
柚子销售超过或不足计划量情况(单位:千克) +3 -6 -2 +11 -7 +13 +5
(1)小王第一周销售柚子最多的一天比最少的一天多销售多少千克?
(2)小王第一周实际销售柚子的总量是多少千克?
(3)若小王按9元/千克进行柚子销售,平均运费为4元/千克,则小王第一周销售柚子一共收入多少元?
23.(2016七上·肇源月考)有一个半圆形的水池,量得它的周长是10.28米,这个水池的半径是多少米?(π取3.14)
答案解析部分
1.【答案】C
【知识点】有理数混合运算法则(含乘方)
2.【答案】B
【知识点】有理数混合运算法则(含乘方)
3.【答案】C
【知识点】有理数的乘法运算律;有理数的加减乘除混合运算的法则;有理数混合运算法则(含乘方)
4.【答案】D
【知识点】有理数的加减乘除混合运算的法则
5.【答案】C
【知识点】有理数混合运算法则(含乘方)
6.【答案】B
【知识点】计算器-有理数的混合运算
7.【答案】B
【知识点】有理数的加减乘除混合运算的法则
8.【答案】A
【知识点】有理数的加减乘除混合运算的法则
9.【答案】B
【知识点】有理数的加减乘除混合运算的法则
10.【答案】A
【知识点】有理数的加减乘除混合运算的法则
11.【答案】
【知识点】有理数混合运算法则(含乘方)
12.【答案】
【知识点】有理数混合运算法则(含乘方)
13.【答案】8
【知识点】含括号的有理数混合运算
14.【答案】
【知识点】有理数的加减乘除混合运算的法则
15.【答案】
【知识点】有理数的加减乘除混合运算的法则
16.【答案】86;38
【知识点】有理数混合运算的实际应用
17.【答案】(1)
(2)
(3)
(4)
【知识点】有理数混合运算法则(含乘方)
18.【答案】(1)解:
=2-9-6
=-13
(2)解:
【知识点】有理数的乘法运算律;有理数混合运算法则(含乘方)
19.【答案】(1)
(2);
(3);
(4);
【知识点】有理数的加减乘除混合运算的法则
20.【答案】(1)解:10×5+4﹣3﹣5+7﹣8=45(箱),
答:根据记录的数据可知前五天共卖出45箱;
(2)解:4﹣3﹣5+7﹣8+21﹣6=10>0,
答:本周实际销售总量达到了计划数量;
(3)解:(10×7+10)×80﹣(10×7+10)×7=5840(元),
答:该果农本周总共收入5840元.
【知识点】有理数混合运算的实际应用
21.【答案】(1)⑥;③
(2)
(3)
【知识点】有理数混合运算的实际应用;正数、负数的实际应用;有理数大小比较的实际应用;有理数减法的实际应用
22.【答案】(1)解:周六销售柚子最多,销售量为(千克),
最少的是周五,销售量为(千克),
所以最多的一天比最少的一天多销售(千克),
【或(千克)】
答:小王第一周销售柚子最多的一天比最少的一天多销售20千克;
(2)解:(千克),
答:小王第一周实际销售柚子的总量是717千克;
(3)解:(元),
答:小王第一周销售柚子一共收入3585元.
【知识点】有理数混合运算的实际应用
23.【答案】解:设半圆的半径为 米,根据题意得
答:这个水池的半径是2米
【知识点】有理数混合运算的实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2.6 有理数的混合运算
一、单选题
1.(2023七上·平泉期末)计算:( ).
A.0 B. C. D.
2.现规定一种新运算“※”:a※ 如 则 ※ 的值为 ( )
A.4 B.3 C.1 D.-1
3.(2024七上·西山月考)在数学课上,老师让甲、乙、丙、丁四位同学分别做了一道有理数运算题,你认为做对的同学是( )
甲:;
乙:;
丙:;
丁:.
A.甲 B.乙 C.丙 D.丁
4.(2024·和平模拟)计算的结果等于( )
A. B. C. D.
5.(2024七上·韶山月考)计算:( )
A. B. C.0 D.2
6.在计算器的键盘中,表示开启电源的键是( )
A.OFF B.AC/ON C.MODE D.SHIFT
7.把(﹣8)﹣(+4)+(﹣5)﹣(﹣2)写成省略加号的形式是( )
A.﹣8+4﹣5+2 B.﹣8﹣4﹣5+2
C.﹣8﹣4+5+2 D.8﹣4﹣5+2
8.(2020七上·怀宁期末)下列运算中正确的是( ).
A.8-(-2)=8+2 B.(-5)÷( )=-5×2
C.(-3)×(-4)=-7 D.2-7=(+2)+(+7)
9.若|x|=3,y2=4,且x+y<0,则xy的值为( )
A.6 B.±6 C.-6 D.3
10.(2022七上·蜀山期末)九宫格起源于中国古代的神秘图案河图和洛书.如图,将,,,,,,,,填入九宫格内,使每行、每列、每条对角线上三个数的和都相等,则的值为( )
A. B. C. D.
二、填空题
11.(2024六下·哈尔滨月考)等于 .
12.(2024七上·黄陂月考)计算:
13.规定图表示运算a-b-c,图形表示运算x-z-y+w.则+= (直接写出答案).
14.(2023七上·阿图什期末)现定义两种新运算“”和“”,对任意有理数a,b,规定:,,例如:,,那么 .
15.(2023七上·义乌)如图所示是计算机某计算程序,若开始输入,则最后输出的结果是 .
16.(2024八下·海淀月考)某单位承担了一项施工任务,完成该任务共需A,B,C,D,E,F,G七道工序,施工要求如下:
①先完成工序A,B,C,再完成工序D,E,F,最后完成工序G;
②完成工序A后方可进行工序B,工序C可与工序A,B同时进行;
③完成工序D后方可进行工序E,工序F可与工序D,E同时进行;
④完成各道工序所需时间如下表所示:
工序 A B C D E F G
所需时间/天 11 15 28 17 16 31 25
(1)在不考虑其它因素的前提下,该施工任务最少 天完成;
(2)现因情况有变,需将工期缩短到80天,工序A,C,D每缩短1天需增加的投入分别为5万元,4万元,6万元,其余工序所需时间不可缩短,则所增加的投入最少是 万元.
三、计算题
17.(2024七上·苏州期中)计算:
(1)
(2)
(3)
(4)
18.(2022七上·博白期末)计算:
(1)
(2)
19.(2024七上·成都期中)观察下列式子:
将以上三个等式两边分别相加得:
.
(1)直接写出结果:_______;
(2)请用上述方法计算(写出具体过程):______;;
(3)直接写出计算结果:_______;
(4)直接写出计算结果:________;
四、解答题
20.(2023七上·吴兴期中)某果农把自家果园的柑橘包装后放到了网上销售.原计划每天卖10箱,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某个星期的销售情况(超额记为正,不足记为负,单位:箱).
星期 一 二 三 四 五 六 日
与计划量的差值 +4 ﹣3 ﹣5 +7 ﹣8 +21 ﹣6
(1)根据记录的数据可知前五天共卖出多少箱?
(2)本周实际销售总量达到了计划数量没有?
(3)若每箱柑橘售价为80元,同时需要支出运费7元/箱,那么该果农本周总共收入多少元?
21.(2024七上·苏州期中)某校七年级男子篮球队共有10名队员,经测量他们的身高如下表(以为基准,超过的记为正数,不足的记为负数):
球员序号 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩
身高与基准的差 (单位:cm) 0 0
(1)观察以上数据可以发现,这10名队员中,身高最高的是 (填球员序号),最矮的是 (填球员序号);
(2)身高最高的队员比最矮的队员高多少?
(3)求该年级男子篮球队队员的平均身高.
22.(2023七上·庐江期中)科技改变生活,当前网络销售日益盛行,许多农商采用网上销售的方式进行营销,实现脱贫致富.小王把自家种的柚子放到网上销售,计划每天销售100千克,但实际每天的销售量与计划销售量相比有增减,超过计划量记为正,不足计划量记为负.如表是小王第一周柚子的销售情况:
星期 一 二 三 四 五 六 日
柚子销售超过或不足计划量情况(单位:千克) +3 -6 -2 +11 -7 +13 +5
(1)小王第一周销售柚子最多的一天比最少的一天多销售多少千克?
(2)小王第一周实际销售柚子的总量是多少千克?
(3)若小王按9元/千克进行柚子销售,平均运费为4元/千克,则小王第一周销售柚子一共收入多少元?
23.(2016七上·肇源月考)有一个半圆形的水池,量得它的周长是10.28米,这个水池的半径是多少米?(π取3.14)
答案解析部分
1.【答案】C
【知识点】有理数混合运算法则(含乘方)
2.【答案】B
【知识点】有理数混合运算法则(含乘方)
3.【答案】C
【知识点】有理数的乘法运算律;有理数的加减乘除混合运算的法则;有理数混合运算法则(含乘方)
4.【答案】D
【知识点】有理数的加减乘除混合运算的法则
5.【答案】C
【知识点】有理数混合运算法则(含乘方)
6.【答案】B
【知识点】计算器-有理数的混合运算
7.【答案】B
【知识点】有理数的加减乘除混合运算的法则
8.【答案】A
【知识点】有理数的加减乘除混合运算的法则
9.【答案】B
【知识点】有理数的加减乘除混合运算的法则
10.【答案】A
【知识点】有理数的加减乘除混合运算的法则
11.【答案】
【知识点】有理数混合运算法则(含乘方)
12.【答案】
【知识点】有理数混合运算法则(含乘方)
13.【答案】8
【知识点】含括号的有理数混合运算
14.【答案】
【知识点】有理数的加减乘除混合运算的法则
15.【答案】
【知识点】有理数的加减乘除混合运算的法则
16.【答案】86;38
【知识点】有理数混合运算的实际应用
17.【答案】(1)
(2)
(3)
(4)
【知识点】有理数混合运算法则(含乘方)
18.【答案】(1)解:
=2-9-6
=-13
(2)解:
【知识点】有理数的乘法运算律;有理数混合运算法则(含乘方)
19.【答案】(1)
(2);
(3);
(4);
【知识点】有理数的加减乘除混合运算的法则
20.【答案】(1)解:10×5+4﹣3﹣5+7﹣8=45(箱),
答:根据记录的数据可知前五天共卖出45箱;
(2)解:4﹣3﹣5+7﹣8+21﹣6=10>0,
答:本周实际销售总量达到了计划数量;
(3)解:(10×7+10)×80﹣(10×7+10)×7=5840(元),
答:该果农本周总共收入5840元.
【知识点】有理数混合运算的实际应用
21.【答案】(1)⑥;③
(2)
(3)
【知识点】有理数混合运算的实际应用;正数、负数的实际应用;有理数大小比较的实际应用;有理数减法的实际应用
22.【答案】(1)解:周六销售柚子最多,销售量为(千克),
最少的是周五,销售量为(千克),
所以最多的一天比最少的一天多销售(千克),
【或(千克)】
答:小王第一周销售柚子最多的一天比最少的一天多销售20千克;
(2)解:(千克),
答:小王第一周实际销售柚子的总量是717千克;
(3)解:(元),
答:小王第一周销售柚子一共收入3585元.
【知识点】有理数混合运算的实际应用
23.【答案】解:设半圆的半径为 米,根据题意得
答:这个水池的半径是2米
【知识点】有理数混合运算的实际应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
