2025年秋浙教版八年级数学上册 第4章 图形与坐标 综合测试卷(含答案)
文档属性
| 名称 | 2025年秋浙教版八年级数学上册 第4章 图形与坐标 综合测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 77.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-25 07:32:43 | ||
图片预览




文档简介
一、选择题(每题3分,共30分)
1.[2025宁波期末]元旦期间,小宁想去王阳明故居纪念馆参观,以下表示王阳明故居纪念馆位置最合理的是( )
A.东经121°08′,北纬30°03′ B.在余姚博物馆的东北方向
C.距离余姚北站约6公里 D.在浙江省
2.下列各点在第一象限内的是( )
A.(1,3) B.(-1,-3) C.(1,-3) D.(-1,3)
3.如图,一艘船在A处遇险后,立即向相距50 nmile位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置是( )
A.北偏东15°,50 nmile B.南偏东15°,50 nmile
C.南偏西15°,50 nmile D.北偏西15°,50 nmile
(第3题) (第4题) (第5题)
4.将如图所示的围棋盘放置在某个平面直角坐标系内,如果白棋②的坐标为(5,2),白棋③的坐标为(6,-2),那么黑棋①的坐标应该是( )
A.(9,3) B.(-1,-1) C.(-1,3) D.(9,-1)
5.在如图所示的平面直角坐标系中,△ABC经过平移后得到△A1B1C1(两个三角形的顶点都在格点上),已知在AC上一点P(2.4,2)平移后的对应点为P1,则点P1的坐标为( )
A.(-0.4,-1) B.(-1.5,-1)
C.(-2.4,-2) D.(-1.6,-1)
6.在平面直角坐标系中,点A(-2,3),B(2,-1),经过点A的直线a∥x轴,点C是直线a上的一个动点,连结BC,当线段BC的长度最短时,点C的坐标为( )
A.(0,-1) B.(-1,-2) C.(-2,-1) D.(2,3)
7.四盏灯笼悬挂点的位置如图.已知A,B,C,D的坐标分别是(-1,b),(1,b),(2,b),(3.5,b),移动y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则移动的方法可以是( )
A.将B移到(-2,b) B.将D移到(-2,b)
C.将C移到(-2,b) D.将B移到(-3.5,b)
(第7题) (第8题) (第10题)
8.如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a与b的数量关系为( )
A.6a-2b=1 B.6a+2b=1 C.6a-b=1 D.6a+b=1
9.在平面直角坐标系xOy中,已知点A(2,-2),在y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有( )
A.1个 B.2个 C.3个 D.4个
10.蜂巢结构精巧,其巢房横截面的形状均为正六边形(各内角为120°,各边相等).如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点P,Q,M均为正六边形的顶点.若点P,Q的坐标分别为(-2,3),(0,-3),则点M的坐标为( )
A.(3,-2) B.(3,2)
C.(2,-3) D.(-2,-3)
二、填空题(每题4分,共24分)
11.在平面直角坐标系中,点P(-3,2)在第________象限,点P到x轴的距离是________.
12.在平面直角坐标系中,点A是x轴上的点,则点A的坐标可以是________.(写出一个即可)
13.[2025金华月考]已知点P(3,-2)与点Q关于y轴对称,则点Q的坐标为________.
14.若点A(a,2)向右平移2个单位长度后所得的点位于第一象限,且点A关于x轴的对称点在第三象限,则a的取值范围是________.
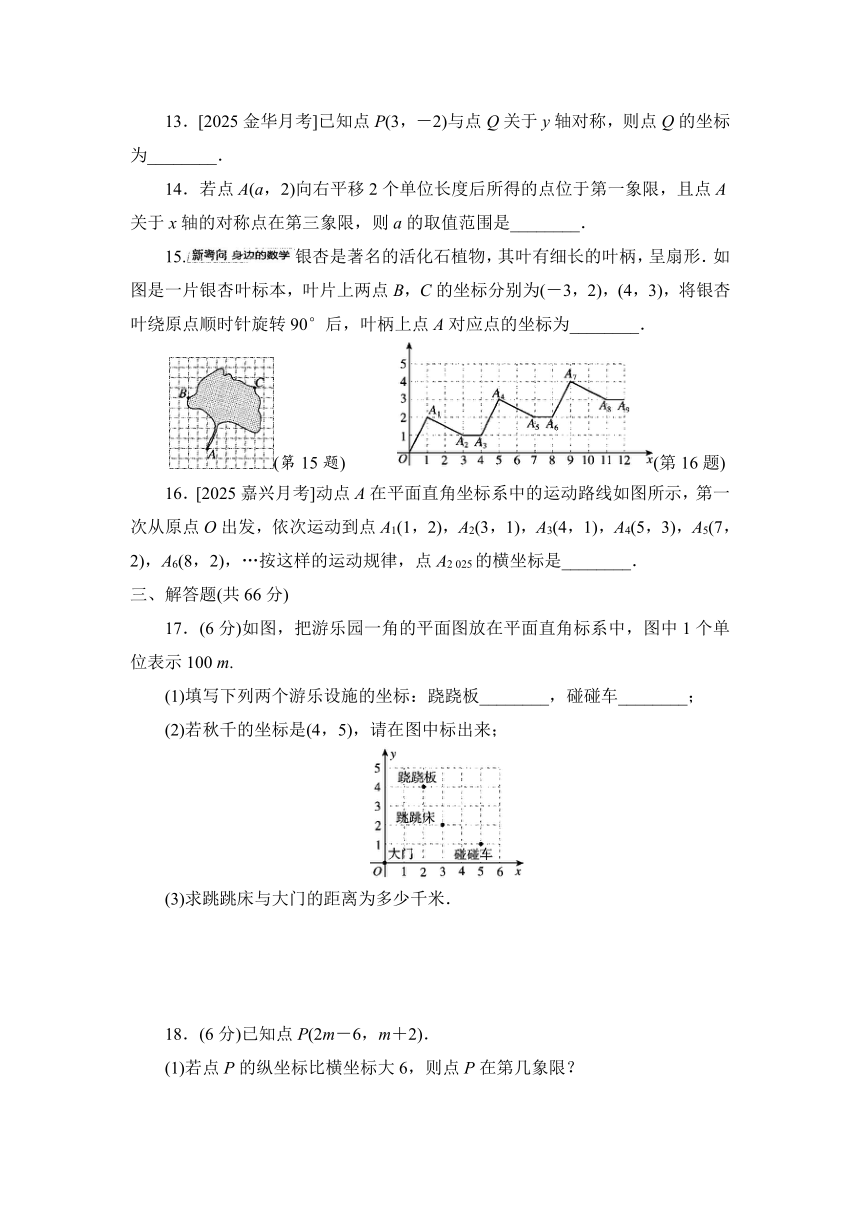
15.银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如图是一片银杏叶标本,叶片上两点B,C的坐标分别为(-3,2),(4,3),将银杏叶绕原点顺时针旋转90°后,叶柄上点A对应点的坐标为________.
(第15题) (第16题)
16.[2025嘉兴月考]动点A在平面直角坐标系中的运动路线如图所示,第一次从原点O出发,依次运动到点A1(1,2),A2(3,1),A3(4,1),A4(5,3),A5(7,2),A6(8,2),…按这样的运动规律,点A2 025的横坐标是________.
三、解答题(共66分)
17.(6分)如图,把游乐园一角的平面图放在平面直角标系中,图中1个单位表示100 m.
(1)填写下列两个游乐设施的坐标:跷跷板________,碰碰车________;
(2)若秋千的坐标是(4,5),请在图中标出来;
(3)求跳跳床与大门的距离为多少千米.
18.(6分)已知点P(2m-6,m+2).
(1)若点P的纵坐标比横坐标大6,则点P在第几象限?
(2)已知点Q(4,3),且PQ∥y轴,求点P的坐标.
19.(6分)[2025杭州月考]如图,A(-3,2),B(-1,-2),C(1,-1).将△ABC先向右平移3个单位长度,再向上平移1个单位长度,可以得到△A1B1C1.
(1)在图中画出△A1B1C1;
(2)求△ABB1的面积.
20.(8分)已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+b)2 025的值.
21.(8分)[2025温州期末]在平面直角坐标系xOy中,O为坐标原点,点A(-4,21-5a)位于第三象限,点B(-4,-a+6)位于第二象限,且a为整数.
(1)求点A和点B的坐标.
(2)若点C(m,0)为x轴上一点,且△ABC是以BC为底边的等腰三角形,求m的值.
22.(10分)如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,边CD与y轴交于点G,点A的坐标为(-2,0),点E在边CD上.将△BCE沿BE所在直线折叠,点C恰好落在点F(0,6)处.
(1)求正方形的边长;
(2)求点E的坐标.
23.(10分)阅读下列文字,回答问题.
已知平面内两点P1(X1,Y1),P2(X2,Y2),则这两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴时,这两点间距离公式可简化为|X1-X2|或|Y1-Y2|.
(1)已知A,B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为-1,试求A,B两点间的距离.
(2)已知一个三角形各顶点坐标分别为C(1,-2),D(3,2),E(-1,4),你能判断△CDE的形状吗?说明理由.
(3)在(2)的条件下,在x轴上找一点P,使PD+PE的值最小,求PD+PE的最小值.
24.(12分)在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,0).
(1)如图①,平移线段AB到线段DC,使点A的对应点为D,点B的对应点为C,若点C的坐标为(-2,4),则点D的坐标为________.
(2)平移线段AB到线段DC,使点C在y轴的正半轴上,点D在第二象限内,连结BC,BD,如图②,若△BCD的面积为7,求点C,D的坐标.
(3)在(2)的条件下,在y轴上是否存在一点P,使△PBD与△BCD的面积之比为12∶7?若存在,求出点P的坐标;若不存在,请说明理由.
答案
一、1.A 2.A 3.C 4.D 5.D 6.D 7.B 8.B 9.D 10.A
二、11.二;2 12.(1,0)(答案不唯一) 13.(-3,-2)
14.-216.2 700 【点拨】根据点A1(1,2),A2(3,1),A3(4,1),A4(5,3),A5(7,2),A6(8,2)的运动规律,
可知从A1到A2 025,横坐标的变化规律依次是+2、+1、+1、+2、…,从A1到A2 025的横坐标共增加了2 025-1=2 024(次).
因为2 024÷3=674……2,所以A2 024的横坐标为1+674×(2+1+1)+2+1=2 700.
三、17.【解】(1)(2,4);(5,1)
(2)如图所示.
(3)跳跳床与大门的距离为=(km).
18.【解】(1)由题意可得m+2-(2m-6)=6,
解得m=2,则2m-6=-2,m+2=4,
所以点P的坐标为(-2,4),所以点P在第二象限.
(2)因为PQ∥y轴,所以点P与点Q的横坐标相等,即2m-6=4,
解得m=5,则m+2=7,所以点P的坐标为(4,7).
19.【解】(1)如图,△A1B1C1即为所作.
(2)如图,S△ABB1=×(1+4)×5-×4×2-×3×1=7.
20.【解】(1)因为点A,B关于x轴对称,
所以解得
(2)因为点A,B关于y轴对称,
所以解得
所以(4a+b)2025==-1.
21.【解】(1)因为点A(-4,21-5a)位于第三象限,
点B(-4,-a+6)位于第二象限,
所以,解得因为a为整数,所以a=5,所以易知A(-4,-4),B(-4,1).
(2)因为A(-4,-4),B(-4,1),所以AB=1-(-4)=5.
因为点C(m,0)为x轴上一点,且△ABC是以BC为底的等腰三角形,所以AC=AB=5.
因为AC=,所以(m+4)2+16=25,
解得m1=-1,m2=-7.所以m的值为-1或-7.
22.【解】(1)设正方形的边长为a,则OB=AB-OA=a-2,
由折叠得FB=CB=a.易知OF=6.
在Rt△OBF中,OF2+OB2=BF2,
即62+(a-2)2=a2,解得a=10.
所以正方形的边长是10.
(2)设GE=m.
易知DG=OA=2,OG=10,所以GF=4.
由折叠的性质,得EF=EC=CD-DG-GE=10-2-m=8-m,在Rt△GEF中,GE2+GF2=EF2,即m2+42=(8-m)2,解得m=3,所以GE=3.所以E(3,10).
23.【解】(1)因为AB∥y轴,点A的纵坐标为4,点B的纵坐标为-1,
所以AB=|4-(-1)|=5.
(2)根据两点间的距离公式可得CD=,DE=,CE=,所以CD=DE,CE2=CD2+DE2,
所以△CDE是等腰直角三角形.
(3)作点D(3,2)关于x轴的对称点D1(3,-2),连结D1E交x轴于点P.
易知此时PD+PE的值最小,最小值为D1E的长.根据两点间的距离公式可得D1E=,所以PD+PE的最小值为.
24.【解】(1)(-4,2)
(2)因为点C在y轴上,B(3,0),所以点B向左平移3个单位长度,所以点A也向左平移3个单位长度,即点D的横坐标为1-3=-2.
因为点D在第二象限,
所以设点A向上平移了(2+y)个单位长度,
则线段AB向左平移3个单位长度,向上平移(2+y)个单位长度得到线段CD,
所以C(0,2+y),D(-2,y),易知OB=3,OC=2+y,
连结OD.因为S△BCD=S△BOC+S△COD-S△BOD=7,
所以OB×OC+OC×2-OB×y=7,
即×3×(2+y)+×2×(2+y)-×3y=7,
所以y=2,所以C(0,4),D(-2,2).
(3)存在.由(2)得D(-2,2),
因为S△BCD=7,=,所以S△PBD=12.
如图①,当点P在x轴上方时,连结OD,
则×OP×2+×3×OP-×3×2=12,解得OP=6,所以P(0,6);
如图②,当点P在x轴下方时,连结OD,
则×OP×2+×3×OP+×3×2=12,解得OP=,所以P.
综上,点P的坐标为(0,6)或.
1.[2025宁波期末]元旦期间,小宁想去王阳明故居纪念馆参观,以下表示王阳明故居纪念馆位置最合理的是( )
A.东经121°08′,北纬30°03′ B.在余姚博物馆的东北方向
C.距离余姚北站约6公里 D.在浙江省
2.下列各点在第一象限内的是( )
A.(1,3) B.(-1,-3) C.(1,-3) D.(-1,3)
3.如图,一艘船在A处遇险后,立即向相距50 nmile位于B处的救生船报警,用方向和距离描述遇险船相对于救生船的位置是( )
A.北偏东15°,50 nmile B.南偏东15°,50 nmile
C.南偏西15°,50 nmile D.北偏西15°,50 nmile
(第3题) (第4题) (第5题)
4.将如图所示的围棋盘放置在某个平面直角坐标系内,如果白棋②的坐标为(5,2),白棋③的坐标为(6,-2),那么黑棋①的坐标应该是( )
A.(9,3) B.(-1,-1) C.(-1,3) D.(9,-1)
5.在如图所示的平面直角坐标系中,△ABC经过平移后得到△A1B1C1(两个三角形的顶点都在格点上),已知在AC上一点P(2.4,2)平移后的对应点为P1,则点P1的坐标为( )
A.(-0.4,-1) B.(-1.5,-1)
C.(-2.4,-2) D.(-1.6,-1)
6.在平面直角坐标系中,点A(-2,3),B(2,-1),经过点A的直线a∥x轴,点C是直线a上的一个动点,连结BC,当线段BC的长度最短时,点C的坐标为( )
A.(0,-1) B.(-1,-2) C.(-2,-1) D.(2,3)
7.四盏灯笼悬挂点的位置如图.已知A,B,C,D的坐标分别是(-1,b),(1,b),(2,b),(3.5,b),移动y轴右侧的一盏灯笼,使得y轴两侧的灯笼对称,则移动的方法可以是( )
A.将B移到(-2,b) B.将D移到(-2,b)
C.将C移到(-2,b) D.将B移到(-3.5,b)
(第7题) (第8题) (第10题)
8.如图,在平面直角坐标系中,以点O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P,若点P的坐标为(6a,2b-1),则a与b的数量关系为( )
A.6a-2b=1 B.6a+2b=1 C.6a-b=1 D.6a+b=1
9.在平面直角坐标系xOy中,已知点A(2,-2),在y轴上确定一点P,使△AOP为等腰三角形,则符合条件的点P有( )
A.1个 B.2个 C.3个 D.4个
10.蜂巢结构精巧,其巢房横截面的形状均为正六边形(各内角为120°,各边相等).如图是部分巢房的横截面图,图中7个全等的正六边形不重叠且无缝隙,将其放在平面直角坐标系中,点P,Q,M均为正六边形的顶点.若点P,Q的坐标分别为(-2,3),(0,-3),则点M的坐标为( )
A.(3,-2) B.(3,2)
C.(2,-3) D.(-2,-3)
二、填空题(每题4分,共24分)
11.在平面直角坐标系中,点P(-3,2)在第________象限,点P到x轴的距离是________.
12.在平面直角坐标系中,点A是x轴上的点,则点A的坐标可以是________.(写出一个即可)
13.[2025金华月考]已知点P(3,-2)与点Q关于y轴对称,则点Q的坐标为________.
14.若点A(a,2)向右平移2个单位长度后所得的点位于第一象限,且点A关于x轴的对称点在第三象限,则a的取值范围是________.
15.银杏是著名的活化石植物,其叶有细长的叶柄,呈扇形.如图是一片银杏叶标本,叶片上两点B,C的坐标分别为(-3,2),(4,3),将银杏叶绕原点顺时针旋转90°后,叶柄上点A对应点的坐标为________.
(第15题) (第16题)
16.[2025嘉兴月考]动点A在平面直角坐标系中的运动路线如图所示,第一次从原点O出发,依次运动到点A1(1,2),A2(3,1),A3(4,1),A4(5,3),A5(7,2),A6(8,2),…按这样的运动规律,点A2 025的横坐标是________.
三、解答题(共66分)
17.(6分)如图,把游乐园一角的平面图放在平面直角标系中,图中1个单位表示100 m.
(1)填写下列两个游乐设施的坐标:跷跷板________,碰碰车________;
(2)若秋千的坐标是(4,5),请在图中标出来;
(3)求跳跳床与大门的距离为多少千米.
18.(6分)已知点P(2m-6,m+2).
(1)若点P的纵坐标比横坐标大6,则点P在第几象限?
(2)已知点Q(4,3),且PQ∥y轴,求点P的坐标.
19.(6分)[2025杭州月考]如图,A(-3,2),B(-1,-2),C(1,-1).将△ABC先向右平移3个单位长度,再向上平移1个单位长度,可以得到△A1B1C1.
(1)在图中画出△A1B1C1;
(2)求△ABB1的面积.
20.(8分)已知点A(2a-b,5+a),B(2b-1,-a+b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求(4a+b)2 025的值.
21.(8分)[2025温州期末]在平面直角坐标系xOy中,O为坐标原点,点A(-4,21-5a)位于第三象限,点B(-4,-a+6)位于第二象限,且a为整数.
(1)求点A和点B的坐标.
(2)若点C(m,0)为x轴上一点,且△ABC是以BC为底边的等腰三角形,求m的值.
22.(10分)如图,在平面直角坐标系中,正方形ABCD的边AB在x轴上,边CD与y轴交于点G,点A的坐标为(-2,0),点E在边CD上.将△BCE沿BE所在直线折叠,点C恰好落在点F(0,6)处.
(1)求正方形的边长;
(2)求点E的坐标.
23.(10分)阅读下列文字,回答问题.
已知平面内两点P1(X1,Y1),P2(X2,Y2),则这两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴时,这两点间距离公式可简化为|X1-X2|或|Y1-Y2|.
(1)已知A,B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为-1,试求A,B两点间的距离.
(2)已知一个三角形各顶点坐标分别为C(1,-2),D(3,2),E(-1,4),你能判断△CDE的形状吗?说明理由.
(3)在(2)的条件下,在x轴上找一点P,使PD+PE的值最小,求PD+PE的最小值.
24.(12分)在平面直角坐标系中,点A的坐标为(1,-2),点B的坐标为(3,0).
(1)如图①,平移线段AB到线段DC,使点A的对应点为D,点B的对应点为C,若点C的坐标为(-2,4),则点D的坐标为________.
(2)平移线段AB到线段DC,使点C在y轴的正半轴上,点D在第二象限内,连结BC,BD,如图②,若△BCD的面积为7,求点C,D的坐标.
(3)在(2)的条件下,在y轴上是否存在一点P,使△PBD与△BCD的面积之比为12∶7?若存在,求出点P的坐标;若不存在,请说明理由.
答案
一、1.A 2.A 3.C 4.D 5.D 6.D 7.B 8.B 9.D 10.A
二、11.二;2 12.(1,0)(答案不唯一) 13.(-3,-2)
14.-2
可知从A1到A2 025,横坐标的变化规律依次是+2、+1、+1、+2、…,从A1到A2 025的横坐标共增加了2 025-1=2 024(次).
因为2 024÷3=674……2,所以A2 024的横坐标为1+674×(2+1+1)+2+1=2 700.
三、17.【解】(1)(2,4);(5,1)
(2)如图所示.
(3)跳跳床与大门的距离为=(km).
18.【解】(1)由题意可得m+2-(2m-6)=6,
解得m=2,则2m-6=-2,m+2=4,
所以点P的坐标为(-2,4),所以点P在第二象限.
(2)因为PQ∥y轴,所以点P与点Q的横坐标相等,即2m-6=4,
解得m=5,则m+2=7,所以点P的坐标为(4,7).
19.【解】(1)如图,△A1B1C1即为所作.
(2)如图,S△ABB1=×(1+4)×5-×4×2-×3×1=7.
20.【解】(1)因为点A,B关于x轴对称,
所以解得
(2)因为点A,B关于y轴对称,
所以解得
所以(4a+b)2025==-1.
21.【解】(1)因为点A(-4,21-5a)位于第三象限,
点B(-4,-a+6)位于第二象限,
所以,解得
(2)因为A(-4,-4),B(-4,1),所以AB=1-(-4)=5.
因为点C(m,0)为x轴上一点,且△ABC是以BC为底的等腰三角形,所以AC=AB=5.
因为AC=,所以(m+4)2+16=25,
解得m1=-1,m2=-7.所以m的值为-1或-7.
22.【解】(1)设正方形的边长为a,则OB=AB-OA=a-2,
由折叠得FB=CB=a.易知OF=6.
在Rt△OBF中,OF2+OB2=BF2,
即62+(a-2)2=a2,解得a=10.
所以正方形的边长是10.
(2)设GE=m.
易知DG=OA=2,OG=10,所以GF=4.
由折叠的性质,得EF=EC=CD-DG-GE=10-2-m=8-m,在Rt△GEF中,GE2+GF2=EF2,即m2+42=(8-m)2,解得m=3,所以GE=3.所以E(3,10).
23.【解】(1)因为AB∥y轴,点A的纵坐标为4,点B的纵坐标为-1,
所以AB=|4-(-1)|=5.
(2)根据两点间的距离公式可得CD=,DE=,CE=,所以CD=DE,CE2=CD2+DE2,
所以△CDE是等腰直角三角形.
(3)作点D(3,2)关于x轴的对称点D1(3,-2),连结D1E交x轴于点P.
易知此时PD+PE的值最小,最小值为D1E的长.根据两点间的距离公式可得D1E=,所以PD+PE的最小值为.
24.【解】(1)(-4,2)
(2)因为点C在y轴上,B(3,0),所以点B向左平移3个单位长度,所以点A也向左平移3个单位长度,即点D的横坐标为1-3=-2.
因为点D在第二象限,
所以设点A向上平移了(2+y)个单位长度,
则线段AB向左平移3个单位长度,向上平移(2+y)个单位长度得到线段CD,
所以C(0,2+y),D(-2,y),易知OB=3,OC=2+y,
连结OD.因为S△BCD=S△BOC+S△COD-S△BOD=7,
所以OB×OC+OC×2-OB×y=7,
即×3×(2+y)+×2×(2+y)-×3y=7,
所以y=2,所以C(0,4),D(-2,2).
(3)存在.由(2)得D(-2,2),
因为S△BCD=7,=,所以S△PBD=12.
如图①,当点P在x轴上方时,连结OD,
则×OP×2+×3×OP-×3×2=12,解得OP=6,所以P(0,6);
如图②,当点P在x轴下方时,连结OD,
则×OP×2+×3×OP+×3×2=12,解得OP=,所以P.
综上,点P的坐标为(0,6)或.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
