第6章 图形的初步知识(新课预习.培优卷)(含解析)-2025-2026学年七年级上册数学浙教版(2024)
文档属性
| 名称 | 第6章 图形的初步知识(新课预习.培优卷)(含解析)-2025-2026学年七年级上册数学浙教版(2024) |

|
|
| 格式 | docx | ||
| 文件大小 | 424.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-04 00:00:00 | ||
图片预览




文档简介
第6章 图形的初步知识
一、选择题
1.下列数学语言,不正确的是( )
A.画直线MN,在直线MN上任取一点P
B.以点M为端点画射线MA
C.直线a,b相交于点m
D.延长线段MN到点P,使NP=MN
2.如图,已知,,且∠COD=10°,则∠AOB等于( )
A.110° B.120° C.130° D.140°
3.如图,在A、B两处观测到C处的方位角分别是( )
A.北偏东65°,北偏西40°
B.北偏东65°,北偏西50°
C.北偏东25°,北偏西40°
D.北偏东35°,北偏西50°
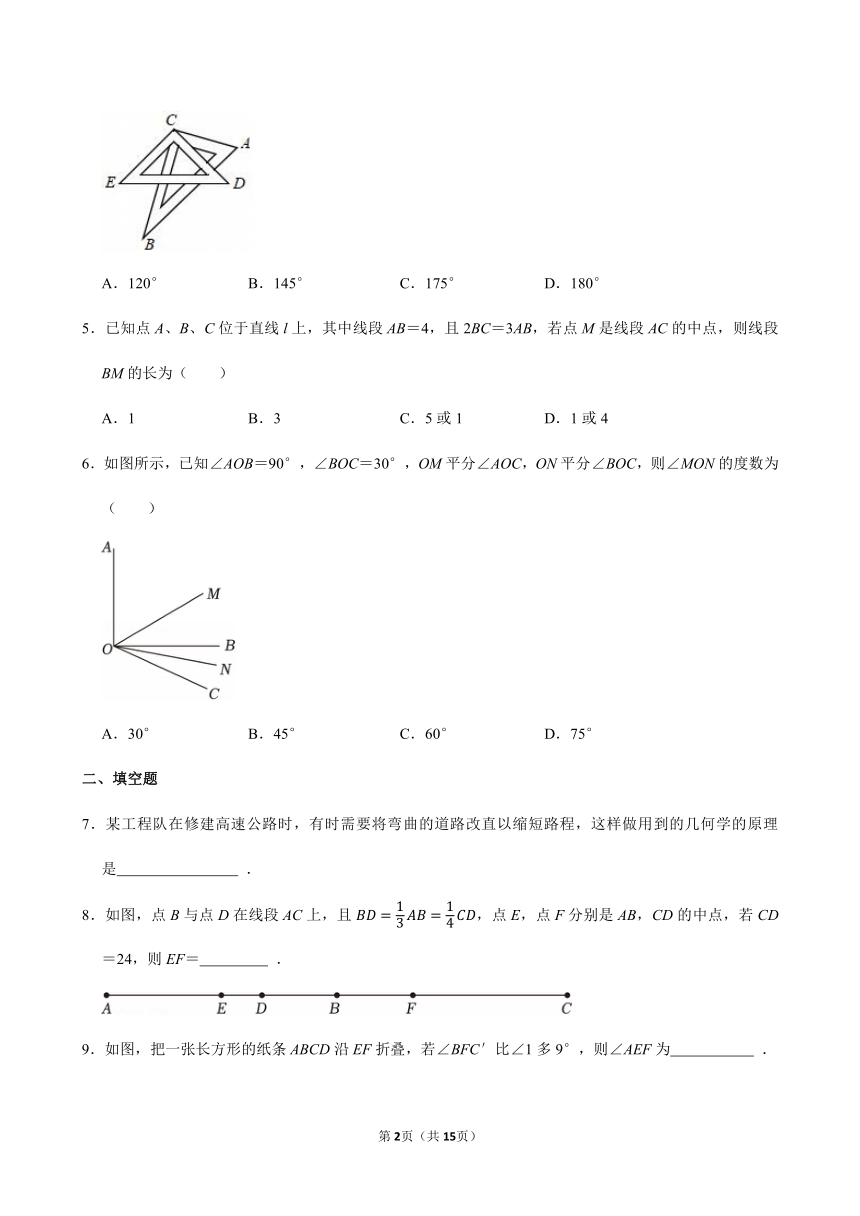
4.如图,将一副三角板叠放在一起,使直角顶点重合于点C,则∠ACE+∠BCD等于( )
A.120° B.145° C.175° D.180°
5.已知点A、B、C位于直线l上,其中线段AB=4,且2BC=3AB,若点M是线段AC的中点,则线段BM的长为( )
A.1 B.3 C.5或1 D.1或4
6.如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为( )
A.30° B.45° C.60° D.75°
二、填空题
7.某工程队在修建高速公路时,有时需要将弯曲的道路改直以缩短路程,这样做用到的几何学的原理是 .
8.如图,点B与点D在线段AC上,且,点E,点F分别是AB,CD的中点,若CD=24,则EF= .
9.如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFC′比∠1多9°,则∠AEF为 .
10.如图,直线AB与CD相交于点O,∠AOC=60°,一直角三角尺EOF的直角顶点与点O重合,OE平分∠AOC,现将三角尺EOF以每秒3°的速度绕点O顺时针旋转,同时直线CD也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(t<40),当CD平分∠EOF时,t的值为 .
三、解答题
11.如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.
12.已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
第6章 图形的初步知识
参考答案与试题解析
一、选择题
1.下列数学语言,不正确的是( )
A.画直线MN,在直线MN上任取一点P
B.以点M为端点画射线MA
C.直线a,b相交于点m
D.延长线段MN到点P,使NP=MN
【答案】C
【分析】根据直线,射线,线段的定义即可得到结论.
【解答】解:A、画直线MN,在直线MN上任取一点P,正确;
B、以点M为端点画射线MA,正确;
C、直线a,b相交于点M,点应该用大写的英文字母表示,故错误;
D、延长线段MN到点P,使NP=MN,正确;
故选:C.
【点评】本题考查了直线,射线,线段,熟记定义是解题的关键.
2.如图,已知,,且∠COD=10°,则∠AOB等于( )
A.110° B.120° C.130° D.140°
【答案】B
【分析】找到题中∠COD的度数是∠AOB的度数的几分之几,再根据∠COD=10°,用分数除法求出结果.
【解答】解:∵,,
∴∠COD=()∠AOB∠AOB,
∴∠AOB=10120°,
故选:B.
【点评】本题考查了角的计算,解题的关键是找到角之间的数量关系再解答.
3.如图,在A、B两处观测到C处的方位角分别是( )
A.北偏东65°,北偏西40°
B.北偏东65°,北偏西50°
C.北偏东25°,北偏西40°
D.北偏东35°,北偏西50°
【答案】B
【分析】根据方向角的定义即可判断.
【解答】解:A处观测到的C处的方向角是:北偏东65°,
B处观测到的C处的方向角是:北偏西50°.
故选:B.
【点评】本题考查了方向角,方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
4.如图,将一副三角板叠放在一起,使直角顶点重合于点C,则∠ACE+∠BCD等于( )
A.120° B.145° C.175° D.180°
【答案】D
【分析】由题意可知∠ACB=∠DCE=90°,根据补角的定义可得∠ACE+∠BCD等于180°.
【解答】解:∵∠ACB=∠DCE=90°,
∴∠ACE+∠BCD=∠DCE+(∠ACD+∠BCD)=∠DCE+∠ACB=180°.
故选:D.
【点评】本题考查了补角,如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
5.已知点A、B、C位于直线l上,其中线段AB=4,且2BC=3AB,若点M是线段AC的中点,则线段BM的长为( )
A.1 B.3 C.5或1 D.1或4
【答案】C
【分析】分两种情况:当点C在点B的右侧时和当点C在点B的左侧时,根据题意,画出图形,再根据线段之间的数量关系,计算即可.
【解答】解:如图,当点C在点B的右侧时,
∵AB=4,且2BC=3AB,
∴BC=6,
∴AC=AB+BC=4+6=10,
∵点M是线段AC的中点,
∴,
∴BM=AM﹣AB=5﹣4=1,
如图,当点C在点B的左侧时,
∵AB=4,且2BC=3AB,
∴BC=6,
∴AC=BC﹣AB=6﹣4=2,
∵点M是线段AC的中点,
∴,
∴BM=AB+AM=4+1=5,
综上所述,线段BM的长为5或1.
故选:C.
【点评】本题考查了线段之间的数量关系,掌握数形结合和分类讨论思想是关键.
6.如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为( )
A.30° B.45° C.60° D.75°
【答案】B
【分析】根据角平分线的定义得到∠MOC∠AOC,∠NOC∠BOC,则∠MON=∠MOC﹣∠NOC(∠AOC﹣∠BOC)∠AOB,然后把∠AOB的度数代入计算即可.
【解答】解:∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC∠AOC,∠NOC∠BOC,
∵∠AOC=∠AOB+∠BOC,
∴∠MON=∠MOC﹣∠NOC(∠AOB+∠BOC﹣∠BOC)∠AOB,
∵∠AOB=90°,
∴∠MON90°=45°.
故选:B.
【点评】本题考查了角平分线的定义,做这类题时学生总会认为条件不够,其实只要把这些等量关系合并化简即可求出角的度数,所以学生做题时有是不要急于计算,而是要先化简后再合并,属于基础题.
二、填空题
7.某工程队在修建高速公路时,有时需要将弯曲的道路改直以缩短路程,这样做用到的几何学的原理是 两点之间,线段最短 .
【答案】见试题解答内容
【分析】此题为数学知识的应用,由题意将弯曲的道路改直以缩短路程,就用到两点间线段最短定理.
【解答】解:弯曲的道路改直,使两点处于同一条线段上,两点之间线段最短.
故答案为:两点之间,线段最短.
【点评】此题主要考查了两点之间线段最短的性质,正确将数学定理应用于实际生活是解题关键.
8.如图,点B与点D在线段AC上,且,点E,点F分别是AB,CD的中点,若CD=24,则EF= 15 .
【答案】15.
【分析】先根据和CD的长分别求出BD、AB和AC的长,然后根据点E,点F分别是AB,CD的中点求出AE和CF的长,最后用AC减去AE和CF就是EF的长.
【解答】解:∵,CD=24,
∴BDCD=6,
∴AB=3BD=18,
∴AC=AB+CD﹣BD=18+24﹣6=36,
∵点E,点F分别是AB,CD的中点,
∴AEAB=9,CFCD=12,
∴EF=AC﹣AE﹣CF=36﹣9﹣12=15.
故答案为:15.
【点评】本题主要考查线段的计算和线段中点定义,熟练掌握线段的和差倍分的计算方法是解决问题的关键.
9.如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFC′比∠1多9°,则∠AEF为 123° .
【答案】见试题解答内容
【分析】∠EFC=x,∠1=y,则∠BFC′=x﹣y,根据“∠BFC′比∠1多9°、∠1与∠EFC互补”得出关于x、y的方程组,解之求得x的值,再根据AD∥BC可得∠AEF=∠EFC.
【解答】解:设∠EFC=x,∠1=y,则∠BFC′=x﹣y,
∵∠BFC′比∠1多9°,
∴x﹣2y=9,
∵x+y=180°,
可得x=123°,即∠1=123°,
∵AD∥BC,
∴∠AEF=∠EFC=123°,
故答案为:123°.
【点评】本题重点考查了平行线的性质及折叠问题,解题的关键是学会利用参数,构建方程组解决问题及平行线的性质.
10.如图,直线AB与CD相交于点O,∠AOC=60°,一直角三角尺EOF的直角顶点与点O重合,OE平分∠AOC,现将三角尺EOF以每秒3°的速度绕点O顺时针旋转,同时直线CD也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(t<40),当CD平分∠EOF时,t的值为 2.5或32.5 .
【答案】2.5或32.5.
【分析】分两种情况进行讨论:当OC平分∠EOF时,∠COE=45°;当OD平分∠EOF 时,∠DOE=45°,分别依据角的和差关系进行列方程即可得到t的值.
【解答】解:∵∠AOC=60°,OE平分∠AOC,
∴∠AOE=30°,
CD平分∠EOF,分两种情况:
①当OC平分∠EOF时,∠COE=45°,
∴∠AOC﹣∠AOE=45°,
即(60°+9°t)﹣(30°+3°t)=45°,
解得t=2.5;
②当OD平分∠EOF时,∠DOE=45°,
∴∠AOC'+∠C'OD﹣∠AOE=45°,
即9°t﹣(180°﹣60°)﹣(30°+3°t)=45°,
解得t=32.5.
综上所述,当CD平分∠EOF时,t的值为2.5或32.5.
故答案为:2.5或32.5.
【点评】本题主要考查了一元一次方程的应用,角平分线的定义,旋转的速度,角度,时间的关系,解题的关键是应用方程的思想解决问题.
三、解答题
11.如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.
【答案】见试题解答内容
【分析】由OM平分∠AOB,ON平分∠DOC可知∠AOM=∠BOM,∠DON=∠CON,可知∠BOM+∠CON=∠AOM+∠DON=∠AOD﹣∠MON,又知∠BOC=∠MON﹣(∠BOM+∠CON),故可得到∠BOC的度数.
【解答】解:∵OM平分∠AOB,ON平分∠DOC,
∴∠AOM=∠BOM,∠DON=∠CON,
∴∠BOM+∠CON=∠AOM+∠DON=∠AOD﹣∠MON=96°﹣68°=28°,
∴∠BOC=∠MON﹣(∠BOM+∠CON)=68°﹣28°=40°.
【点评】本题主要考查了角平分线的定义以及角的和差与运算;熟练掌握角平分线的定义,弄清各个角之间的关系是解决问题的突破口.
12.已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= 4 ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
【答案】见试题解答内容
【分析】(1)根据已知AB=6,CQ=2AQ,CP=2BP,以及线段的中点的定义解答;
(2)根据已知AB=m(m为常数),CQ=2AQ,CP=2BP;
(3)根据题意,画出图形,求得2AP+CQ﹣2PQ=0,即可得出2AP+CQ﹣2PQ与1的大小关系.
【解答】解:(1)∵CQ=2AQ,CP=2BP,
∴CQAC,CPBC,
∵点C恰好在线段AB中点,
∴AC=BCAB,
∵AB=m(m为常数),
∴PQ=CQ+CPACBCABABAB6=4;
故答案为:4;
(2)①点C在线段AB上:
∵CQ=2AQ,CP=2BP,
∴CQAC,CPBC,
∵AB=m(m为常数),
∴PQ=CQ+CPACBC(AC+BC)ABm;
②点C在线段BA的延长线上:
∵CQ=2AQ,CP=2BP,
∴CQAC,CPBC,
∵AB=m(m为常数),
∴PQ=CP﹣CQBCAC(BC﹣AC)ABm;
③点C在线段AB的延长线上:
∵CQ=2AQ,CP=2BP,
∴CQAC,CPBC,
∵AB=m(m为常数),
∴PQ=CQ﹣CPACBC(AC﹣BC)ABm;
故PQ是一个常数,即是常数m;
(3)如图:
∵CQ=2AQ,
∴2AP+CQ﹣2PQ
=2AP+CQ﹣2(AP+AQ)
=2AP+CQ﹣2AP﹣2AQ
=CQ﹣2AQ
=2AQ﹣2AQ
=0,
∴2AP+CQ﹣2PQ<1.
【点评】本题主要考查两点间的距离,掌握线段的中点的性质、线段的和差运算是解题的关键.
第1页(共1页)
一、选择题
1.下列数学语言,不正确的是( )
A.画直线MN,在直线MN上任取一点P
B.以点M为端点画射线MA
C.直线a,b相交于点m
D.延长线段MN到点P,使NP=MN
2.如图,已知,,且∠COD=10°,则∠AOB等于( )
A.110° B.120° C.130° D.140°
3.如图,在A、B两处观测到C处的方位角分别是( )
A.北偏东65°,北偏西40°
B.北偏东65°,北偏西50°
C.北偏东25°,北偏西40°
D.北偏东35°,北偏西50°
4.如图,将一副三角板叠放在一起,使直角顶点重合于点C,则∠ACE+∠BCD等于( )
A.120° B.145° C.175° D.180°
5.已知点A、B、C位于直线l上,其中线段AB=4,且2BC=3AB,若点M是线段AC的中点,则线段BM的长为( )
A.1 B.3 C.5或1 D.1或4
6.如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为( )
A.30° B.45° C.60° D.75°
二、填空题
7.某工程队在修建高速公路时,有时需要将弯曲的道路改直以缩短路程,这样做用到的几何学的原理是 .
8.如图,点B与点D在线段AC上,且,点E,点F分别是AB,CD的中点,若CD=24,则EF= .
9.如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFC′比∠1多9°,则∠AEF为 .
10.如图,直线AB与CD相交于点O,∠AOC=60°,一直角三角尺EOF的直角顶点与点O重合,OE平分∠AOC,现将三角尺EOF以每秒3°的速度绕点O顺时针旋转,同时直线CD也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(t<40),当CD平分∠EOF时,t的值为 .
三、解答题
11.如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.
12.已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
第6章 图形的初步知识
参考答案与试题解析
一、选择题
1.下列数学语言,不正确的是( )
A.画直线MN,在直线MN上任取一点P
B.以点M为端点画射线MA
C.直线a,b相交于点m
D.延长线段MN到点P,使NP=MN
【答案】C
【分析】根据直线,射线,线段的定义即可得到结论.
【解答】解:A、画直线MN,在直线MN上任取一点P,正确;
B、以点M为端点画射线MA,正确;
C、直线a,b相交于点M,点应该用大写的英文字母表示,故错误;
D、延长线段MN到点P,使NP=MN,正确;
故选:C.
【点评】本题考查了直线,射线,线段,熟记定义是解题的关键.
2.如图,已知,,且∠COD=10°,则∠AOB等于( )
A.110° B.120° C.130° D.140°
【答案】B
【分析】找到题中∠COD的度数是∠AOB的度数的几分之几,再根据∠COD=10°,用分数除法求出结果.
【解答】解:∵,,
∴∠COD=()∠AOB∠AOB,
∴∠AOB=10120°,
故选:B.
【点评】本题考查了角的计算,解题的关键是找到角之间的数量关系再解答.
3.如图,在A、B两处观测到C处的方位角分别是( )
A.北偏东65°,北偏西40°
B.北偏东65°,北偏西50°
C.北偏东25°,北偏西40°
D.北偏东35°,北偏西50°
【答案】B
【分析】根据方向角的定义即可判断.
【解答】解:A处观测到的C处的方向角是:北偏东65°,
B处观测到的C处的方向角是:北偏西50°.
故选:B.
【点评】本题考查了方向角,方向角是表示方向的角;以正北,正南方向为基准,来描述物体所处的方向.
4.如图,将一副三角板叠放在一起,使直角顶点重合于点C,则∠ACE+∠BCD等于( )
A.120° B.145° C.175° D.180°
【答案】D
【分析】由题意可知∠ACB=∠DCE=90°,根据补角的定义可得∠ACE+∠BCD等于180°.
【解答】解:∵∠ACB=∠DCE=90°,
∴∠ACE+∠BCD=∠DCE+(∠ACD+∠BCD)=∠DCE+∠ACB=180°.
故选:D.
【点评】本题考查了补角,如果两个角的和等于180°(平角),就说这两个角互为补角.即其中一个角是另一个角的补角.
5.已知点A、B、C位于直线l上,其中线段AB=4,且2BC=3AB,若点M是线段AC的中点,则线段BM的长为( )
A.1 B.3 C.5或1 D.1或4
【答案】C
【分析】分两种情况:当点C在点B的右侧时和当点C在点B的左侧时,根据题意,画出图形,再根据线段之间的数量关系,计算即可.
【解答】解:如图,当点C在点B的右侧时,
∵AB=4,且2BC=3AB,
∴BC=6,
∴AC=AB+BC=4+6=10,
∵点M是线段AC的中点,
∴,
∴BM=AM﹣AB=5﹣4=1,
如图,当点C在点B的左侧时,
∵AB=4,且2BC=3AB,
∴BC=6,
∴AC=BC﹣AB=6﹣4=2,
∵点M是线段AC的中点,
∴,
∴BM=AB+AM=4+1=5,
综上所述,线段BM的长为5或1.
故选:C.
【点评】本题考查了线段之间的数量关系,掌握数形结合和分类讨论思想是关键.
6.如图所示,已知∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,则∠MON的度数为( )
A.30° B.45° C.60° D.75°
【答案】B
【分析】根据角平分线的定义得到∠MOC∠AOC,∠NOC∠BOC,则∠MON=∠MOC﹣∠NOC(∠AOC﹣∠BOC)∠AOB,然后把∠AOB的度数代入计算即可.
【解答】解:∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC∠AOC,∠NOC∠BOC,
∵∠AOC=∠AOB+∠BOC,
∴∠MON=∠MOC﹣∠NOC(∠AOB+∠BOC﹣∠BOC)∠AOB,
∵∠AOB=90°,
∴∠MON90°=45°.
故选:B.
【点评】本题考查了角平分线的定义,做这类题时学生总会认为条件不够,其实只要把这些等量关系合并化简即可求出角的度数,所以学生做题时有是不要急于计算,而是要先化简后再合并,属于基础题.
二、填空题
7.某工程队在修建高速公路时,有时需要将弯曲的道路改直以缩短路程,这样做用到的几何学的原理是 两点之间,线段最短 .
【答案】见试题解答内容
【分析】此题为数学知识的应用,由题意将弯曲的道路改直以缩短路程,就用到两点间线段最短定理.
【解答】解:弯曲的道路改直,使两点处于同一条线段上,两点之间线段最短.
故答案为:两点之间,线段最短.
【点评】此题主要考查了两点之间线段最短的性质,正确将数学定理应用于实际生活是解题关键.
8.如图,点B与点D在线段AC上,且,点E,点F分别是AB,CD的中点,若CD=24,则EF= 15 .
【答案】15.
【分析】先根据和CD的长分别求出BD、AB和AC的长,然后根据点E,点F分别是AB,CD的中点求出AE和CF的长,最后用AC减去AE和CF就是EF的长.
【解答】解:∵,CD=24,
∴BDCD=6,
∴AB=3BD=18,
∴AC=AB+CD﹣BD=18+24﹣6=36,
∵点E,点F分别是AB,CD的中点,
∴AEAB=9,CFCD=12,
∴EF=AC﹣AE﹣CF=36﹣9﹣12=15.
故答案为:15.
【点评】本题主要考查线段的计算和线段中点定义,熟练掌握线段的和差倍分的计算方法是解决问题的关键.
9.如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFC′比∠1多9°,则∠AEF为 123° .
【答案】见试题解答内容
【分析】∠EFC=x,∠1=y,则∠BFC′=x﹣y,根据“∠BFC′比∠1多9°、∠1与∠EFC互补”得出关于x、y的方程组,解之求得x的值,再根据AD∥BC可得∠AEF=∠EFC.
【解答】解:设∠EFC=x,∠1=y,则∠BFC′=x﹣y,
∵∠BFC′比∠1多9°,
∴x﹣2y=9,
∵x+y=180°,
可得x=123°,即∠1=123°,
∵AD∥BC,
∴∠AEF=∠EFC=123°,
故答案为:123°.
【点评】本题重点考查了平行线的性质及折叠问题,解题的关键是学会利用参数,构建方程组解决问题及平行线的性质.
10.如图,直线AB与CD相交于点O,∠AOC=60°,一直角三角尺EOF的直角顶点与点O重合,OE平分∠AOC,现将三角尺EOF以每秒3°的速度绕点O顺时针旋转,同时直线CD也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(t<40),当CD平分∠EOF时,t的值为 2.5或32.5 .
【答案】2.5或32.5.
【分析】分两种情况进行讨论:当OC平分∠EOF时,∠COE=45°;当OD平分∠EOF 时,∠DOE=45°,分别依据角的和差关系进行列方程即可得到t的值.
【解答】解:∵∠AOC=60°,OE平分∠AOC,
∴∠AOE=30°,
CD平分∠EOF,分两种情况:
①当OC平分∠EOF时,∠COE=45°,
∴∠AOC﹣∠AOE=45°,
即(60°+9°t)﹣(30°+3°t)=45°,
解得t=2.5;
②当OD平分∠EOF时,∠DOE=45°,
∴∠AOC'+∠C'OD﹣∠AOE=45°,
即9°t﹣(180°﹣60°)﹣(30°+3°t)=45°,
解得t=32.5.
综上所述,当CD平分∠EOF时,t的值为2.5或32.5.
故答案为:2.5或32.5.
【点评】本题主要考查了一元一次方程的应用,角平分线的定义,旋转的速度,角度,时间的关系,解题的关键是应用方程的思想解决问题.
三、解答题
11.如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.
【答案】见试题解答内容
【分析】由OM平分∠AOB,ON平分∠DOC可知∠AOM=∠BOM,∠DON=∠CON,可知∠BOM+∠CON=∠AOM+∠DON=∠AOD﹣∠MON,又知∠BOC=∠MON﹣(∠BOM+∠CON),故可得到∠BOC的度数.
【解答】解:∵OM平分∠AOB,ON平分∠DOC,
∴∠AOM=∠BOM,∠DON=∠CON,
∴∠BOM+∠CON=∠AOM+∠DON=∠AOD﹣∠MON=96°﹣68°=28°,
∴∠BOC=∠MON﹣(∠BOM+∠CON)=68°﹣28°=40°.
【点评】本题主要考查了角平分线的定义以及角的和差与运算;熟练掌握角平分线的定义,弄清各个角之间的关系是解决问题的突破口.
12.已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足CQ=2AQ,CP=2BP.
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= 4 ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
【答案】见试题解答内容
【分析】(1)根据已知AB=6,CQ=2AQ,CP=2BP,以及线段的中点的定义解答;
(2)根据已知AB=m(m为常数),CQ=2AQ,CP=2BP;
(3)根据题意,画出图形,求得2AP+CQ﹣2PQ=0,即可得出2AP+CQ﹣2PQ与1的大小关系.
【解答】解:(1)∵CQ=2AQ,CP=2BP,
∴CQAC,CPBC,
∵点C恰好在线段AB中点,
∴AC=BCAB,
∵AB=m(m为常数),
∴PQ=CQ+CPACBCABABAB6=4;
故答案为:4;
(2)①点C在线段AB上:
∵CQ=2AQ,CP=2BP,
∴CQAC,CPBC,
∵AB=m(m为常数),
∴PQ=CQ+CPACBC(AC+BC)ABm;
②点C在线段BA的延长线上:
∵CQ=2AQ,CP=2BP,
∴CQAC,CPBC,
∵AB=m(m为常数),
∴PQ=CP﹣CQBCAC(BC﹣AC)ABm;
③点C在线段AB的延长线上:
∵CQ=2AQ,CP=2BP,
∴CQAC,CPBC,
∵AB=m(m为常数),
∴PQ=CQ﹣CPACBC(AC﹣BC)ABm;
故PQ是一个常数,即是常数m;
(3)如图:
∵CQ=2AQ,
∴2AP+CQ﹣2PQ
=2AP+CQ﹣2(AP+AQ)
=2AP+CQ﹣2AP﹣2AQ
=CQ﹣2AQ
=2AQ﹣2AQ
=0,
∴2AP+CQ﹣2PQ<1.
【点评】本题主要考查两点间的距离,掌握线段的中点的性质、线段的和差运算是解题的关键.
第1页(共1页)
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
