浙教版八年级上数学第一章三角形的初步认识单元练习
文档属性
| 名称 | 浙教版八年级上数学第一章三角形的初步认识单元练习 |  | |
| 格式 | zip | ||
| 文件大小 | 383.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-21 17:17:40 | ||
图片预览


文档简介
浙教版八年级上数学第一章三角形的初步认识单元练习
一.选择题(共10小题)
1.(2016?岳阳)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm C.3cm,4cm,8cm D.3cm,3cm,4cm
2.(2014?襄阳)下列命题错误的是( )
A.所有的实数都可用数轴上的点表示 B.等角的补角相等
C.无理数包括正无理数,0,负无理数 D.两点之间,线段最短
3.(2015春?普陀区期末)下列说法正确的是( )
A.两个等边三角形一定全等 B.腰对应相等的两个等腰三角形全等
C.形状相同的两个三角形全等 D.全等三角形的面积一定相等
4.(2014秋?新泰)如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
A.∠1=∠2
B.AC=CA
C.∠D=∠B
D.AC=BC
5.(2016?宁波模拟)如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能
判定△ABD≌△BAC的是( )
A.∠D=∠C
B.BD=AC
C.∠CAD=∠DBC
D.AD=BC
6.(2015?台州)某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( ) 21*cnjy*com
A.若甲对,则乙对 B.若乙对,则甲对
C.若乙错,则甲错 D.若甲错,则乙对
7.(2016春?商水)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
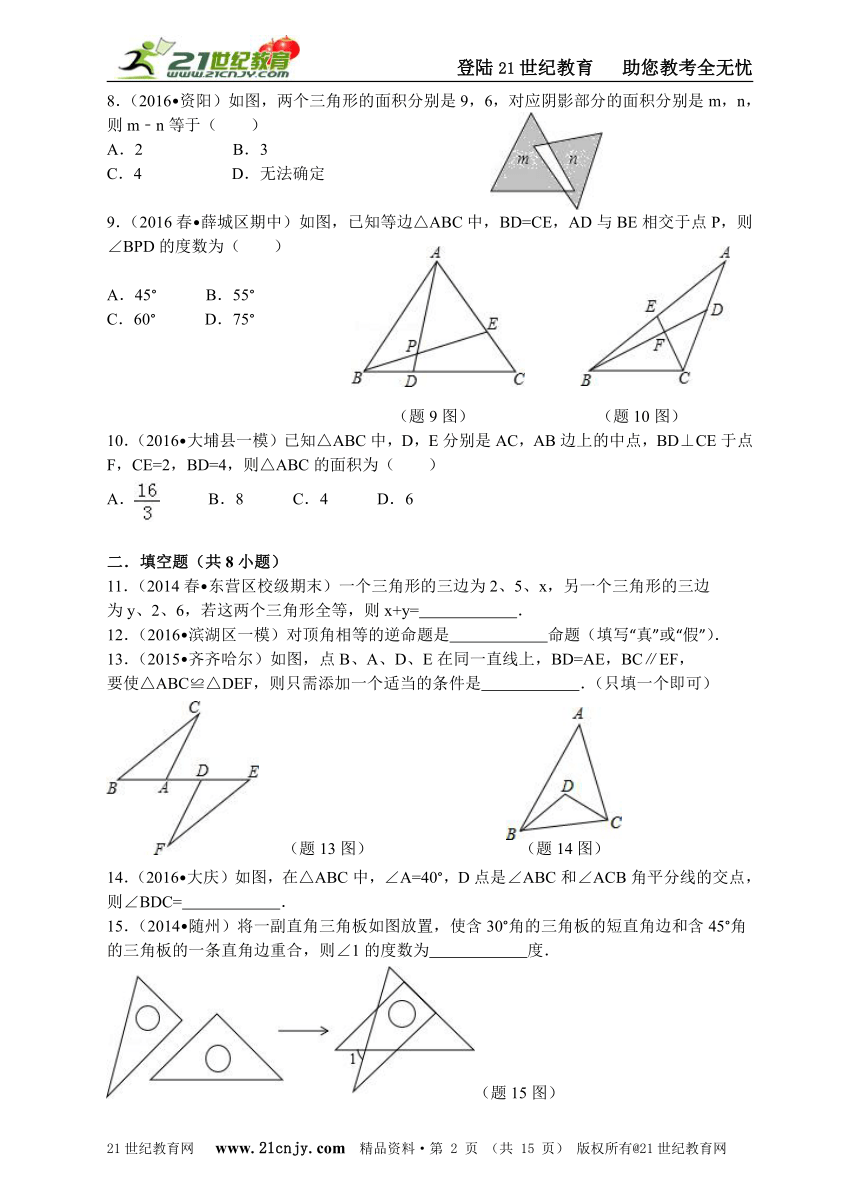
8.(2016?资阳)如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m﹣n等于( )
A.2 B.3
C.4 D.无法确定
9.(2016春?薛城区期中)如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )
A.45° B.55°
C.60° D.75°
(题9图) (题10图)
10.(2016?大埔县一模)已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
A. B.8 C.4 D.6
二.填空题(共8小题)
11.(2014春?东营区校级期末)一个三角形的三边为2、5、x,另一个三角形的三边
为y、2、6,若这两个三角形全等,则x+y= .
12.(2016?滨湖区一模)对顶角相等的逆命题是 命题(填写“真”或“假”).
13.(2015?齐齐哈尔)如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,
要使△ABC≌△DEF,则只需添加一个适当的条件是 .(只填一个即可)
(题13图) (题14图)
14.(2016?大庆)如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= .
15.(2014?随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 度.
(题15图)
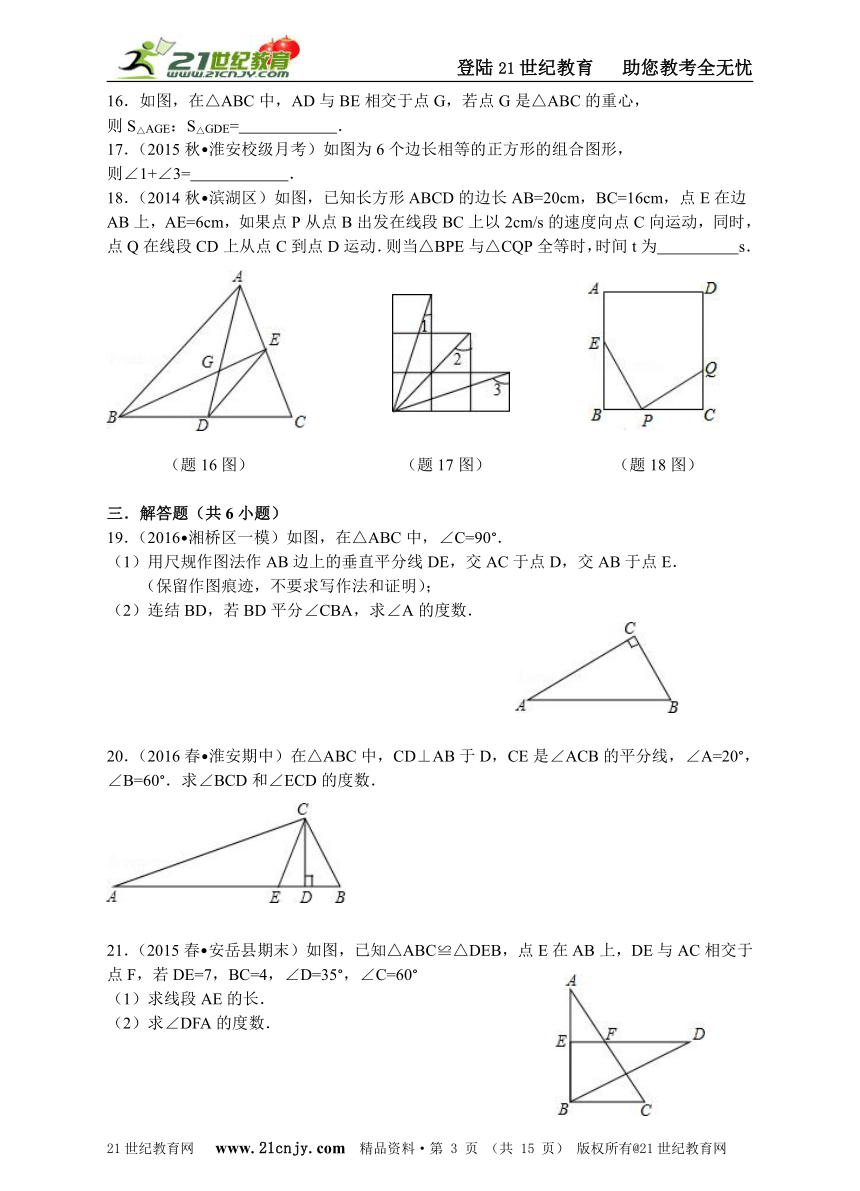
16.如图,在△ABC中,AD与BE相交于点G,若点G是△ABC的重心,
则S△AGE:S△GDE= .
17.(2015秋?淮安校级月考)如图为6个边长相等的正方形的组合图形,
则∠1+∠3= .
18.(2014秋?滨湖区)如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为 s.
(题16图) (题17图) (题18图)
三.解答题(共6小题)
19.(2016?湘桥区一模)如图,在△ABC中,∠C=90°.
(1)用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.
(保留作图痕迹,不要求写作法和证明);
(2)连结BD,若BD平分∠CBA,求∠A的度数.
20.(2016春?淮安期中)在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.【来源:21·世纪·教育·网】
21.(2015春?安岳县期末)如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°2-1-c-n-j-y
(1)求线段AE的长.
(2)求∠DFA的度数.
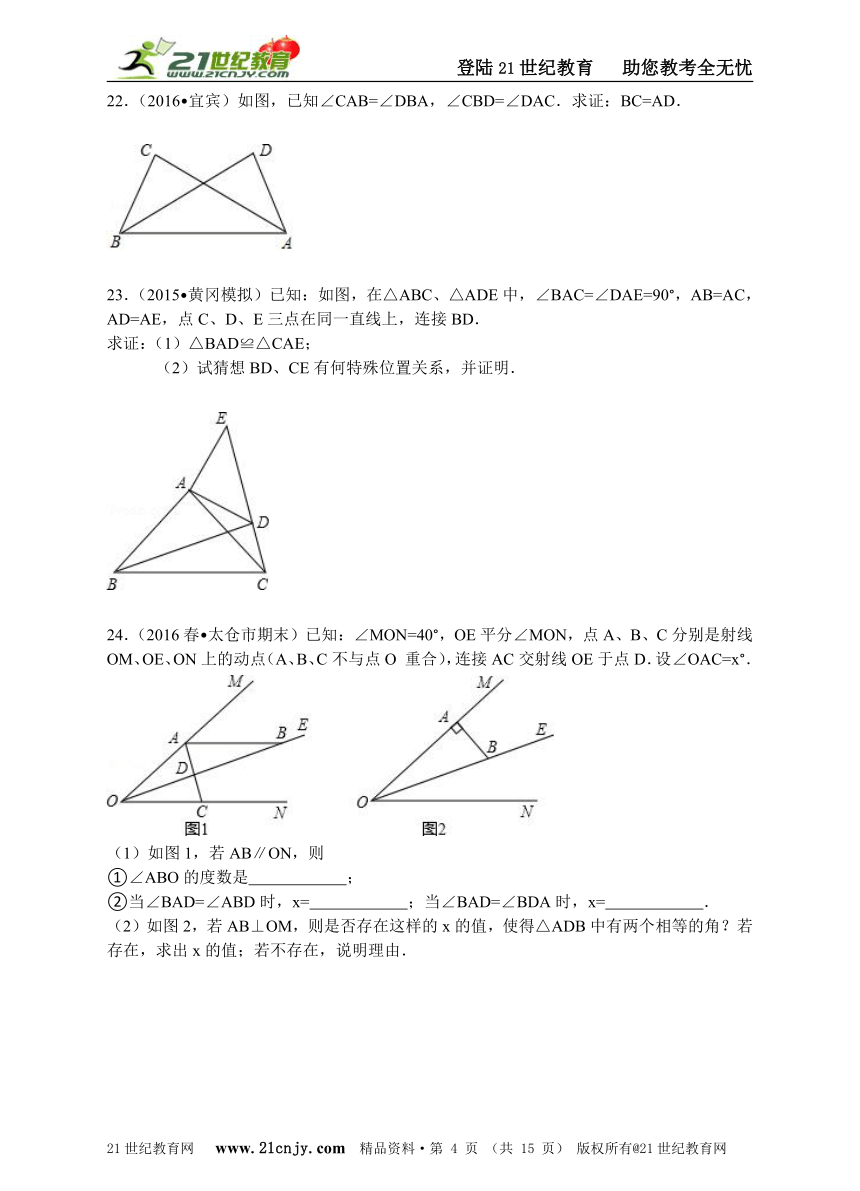
22.(2016?宜宾)如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.
23.(2015?黄冈模拟)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.【版权所有:21教育】
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
24.(2016春?太仓市期末)已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则
①∠ABO的度数是 ;
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
浙教版八年级上数学第一章三角形的初步认识单元练习
参考答案与试题解析
一.选择题(共10小题)
1.(2016?岳阳)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cmB.7cm,4cm,2cmC.3cm,4cm,8cmD.3cm,3cm,4cm
【分析】依据三角形任意两边之和大于第三边求解即可.
【解答】解:A、因为2+3=5,所以不能构成三角形,故A错误;
B、因为2+4<6,所以不能构成三角形,故B错误;
C、因为3+4<8,所以不能构成三角形,故C错误;
D、因为3+3>4,所以能构成三角形,故D正确.故选:D.
【点评】本题主要考查的是三角形的三边关系,掌握三角形的三边关系是解题的关键.
2.(2014?襄阳)下列命题错误的是( )
A.所有的实数都可用数轴上的点表示
B.等角的补角相等
C.无理数包括正无理数,0,负无理数
D.两点之间,线段最短
【点评】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.21·世纪*教育网
3.(2015春?普陀区期末)下列说法正确的是( )
A.两个等边三角形一定全等
B.腰对应相等的两个等腰三角形全等
C.形状相同的两个三角形全等
D.全等三角形的面积一定相等
【分析】根据全等图形的判定和性质对各个选项进行判断即可.
【解答】解:两个等边三角形边长不一定相等,所以不一定全等,A错误;
腰对应相等的两个等腰三角形对应角不一定相等,所以不一定全等,B错误;
形状相同的两个三角形对应边不一定相等,所以不一定全等,C错误;
全等三角形的面积一定相等,所以D正确,故选:D.
【点评】本题考查的是全等图形的判定和性质,对应角相等、对应边相等的两个图形确定,全等形的周长和面积相等.21·cn·jy·com
4.(2014秋?新泰)如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
A.∠1=∠2B.AC=CAC.∠D=∠BD.AC=BC
【分析】由△ABC≌△CDA,并且AB=CD,AC和CA是公共边,可知∠1和∠2,∠D和∠B是对应角.全等三角形的对应角相等,因而前三个选项一定正确.AC和BC不是对应边,不一定相等.2·1·c·n·j·y
【点评】本题主要考查了全等三角形性质;而根据已知条件正确找着对应边、对应角是正确解决本题的关键.
5.(2016?宁波模拟)如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
A.∠D=∠CB.BD=ACC.∠CAD=∠DBCD.AD=BC
【分析】根据图形知道隐含条件BC=BC,根据全等三角形的判定定理逐个判断即可.
【解答】解:A、添加条件∠D=∠C,还有已知条件∠CAB=∠DBA,BC=BC,符合全等三角形的判定定理AAS,能推出△ABD≌△BAC,故本选项错误;21cnjy.com
B、添加条件BD=AC,还有已知条件∠CAB=∠DBA,BC=BC,符合全等三角形的判定定理SAS,能推出△ABD≌△BAC,故本选项错误;
C、∵∠CAB=∠DBA,∠CAD=∠DBC,
∴∠DAB=∠CBA,
还有已知条件∠CAB=∠DBA,BC=BC,符合全等三角形的判定定理ASA,能推出△ABD≌△BAC,故本选项错误;
D、添加条件AD=BC,还有已知条件∠CAB=∠DBA,BC=BC,不符合全等三角形的判定定理,不能推出△ABD≌△BAC,故本选项正确;故选D.
【点评】本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,符合SSA和AAA不能推出两三角形全等.
6.(2015?台州)某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A.若甲对,则乙对B.若乙对,则甲对C.若乙错,则甲错D.若甲错,则乙对
【分析】分别假设甲说的对和乙说的正确,进而得出答案.
【解答】解:若甲对,即只参加一项的人数大于14人,假设只参加一项的人数是15人,
则两项都参加的人数为5人,故乙错.
若乙对,即两项都参加的人数小于5人,则两项都参加的人数至多为4人,
此时只参加一项的人数为16人,故甲对.故选:B.
【点评】此题主要考查了推理与论证,关键是分两种情况分别进行分析.
7.(2016春?商水)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
【分析】根据全等三角形对应边相等,全等三角形对应角相等结合图象解答即可.
【解答】解:∵△ABC≌△AEF,
∴AC=AF,故①正确;∠EAF=∠BAC,
∴∠FAC=∠EAB≠∠FAB,故②错误;EF=BC,故③正确;
∠EAB=∠FAC,故④正确;综上所述,结论正确的是①③④共3个.故选C.
【点评】本题考查了全等三角形的性质,熟记性质并准确识图,准确确定出对应边和对应角是解题的关键.
【分析】设空白出的面积为x,根据题意列出关系式,相减即可求出m﹣n的值.
【解答】解:设空白出图形的面积为x,
根据题意得:m+x=9,n+x=6,则m﹣n=9﹣6=3.故选B.
【点评】本题考查了三角形的面积;设出未知数,根据三角形的面积得出关系式是解决问题的关键.
9.(2016春?薛城区期中)如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )21教育名师原创作品
A.45°B.55°
C.60°D.75°
【分析】根据等边三角形性质得出∠ABD=∠C=60°,AB=BC,证出△ABD≌△BCE,根据全等三角形的性质得出∠BAD=∠CBE,根据三角形外角性质得出∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC,即可得出答案.
【解答】解:∵△ABC是等边三角形,∴∠ABD=∠C=60°,AB=BC,
在△ABD和△BCE中,,∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,∴∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.故选C.
【点评】本题考查了等边三角形的性质,全等三角形的性质和判定,三角形外角性质的应用,解此题的关键是求出△ABD≌△BCE.
【分析】连接ED,根据三角形中位线定理证明△ADE∽△ABC,且相似比为1:2,求出四边形EBCD的面积,根据相似三角形的面积比等于相似比的平方列式计算即可.
【解答】解:连接ED,
∵BD⊥CE,∴四边形EBCD的面积=×BD×CE=4,设△ABC的面积为x,
∵D,E分别是AC,AB边上的中点,∴BC=2DE,ED∥BC,∴△ADE∽△ABC,
△ABC的面积=4×△ADE的面积,即x=4(x﹣4),解得x=.故选:A.
【点评】本题考查的是三角形的中位线的性质和相似三角形的判定和性质,掌握三角形的中位线定理和相似三角形的性质定理是解题的关键.
二.填空题(共8小题)
11.(2014春?东营区校级期末)一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= 11 .
【分析】根据已知条件分清对应边,结合全的三角形的性质可得出答案.
【解答】解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5∴x+y=11.故填11.
【点评】本题考查了全等三角形的性质及对应边的找法;根据两个三角形中都有2找对对应边是解决本题的关键.
12.(2016?滨湖区一模)对顶角相等的逆命题是 假 命题(填写“真”或“假”).
【分析】先根据互逆命题的定义写出对顶角相等的逆命题,再判断真假.
【解答】解:“对顶角相等”的逆命题是:相等的角是对顶角,它是假命题.故答案为:假.
【点评】本题考查了互逆命题及真假命题的定义.两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题;正确的命题叫做真命题,错误的命题叫做假命题.
13.(2015?齐齐哈尔)如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是 BC=EF或∠BAC=∠EDF .(只填一个即可)
【分析】BC=EF或∠BAC=∠EDF,若BC=EF,根据条件利用SAS即可得证;若∠BAC=∠EDF,根据条件利用ASA即可得证.
在△ABC和△DEF中,,∴△ABC≌△DEF(SAS);
若添加∠BAC=∠EDF,∵BC∥EF,∴∠B=∠E,
∵BD=AE,∴BD﹣AD=AE﹣AD,即BA=ED,
在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),
故答案为:BC=EF或∠BAC=∠EDF
【点评】此题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解本题的关键.
14.(2016?大庆)如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= 110° .
【分析】由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70,再利用三角形内角和定理即可求出∠BDC的度数.
【解答】解:∵D点是∠ABC和∠ACB角平分线的交点,
∴有∠CBD=∠ABD=∠ABC,∠BCD=∠ACD=∠ACB,
∴∠ABC+∠ACB=180﹣40=140,∴∠OBC+∠OCB=70,∴∠BOC=180﹣70=110°,
故答案为:110°.
【点评】此题主要考查学生对角平分线性质,三角形内角和定理,三角形的外角性质等知识点的理解和掌握,难度不大,是一道基础题,熟记三角形内角和定理是解决问题的关键.
15.(2014?随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 75 度.www-2-1-cnjy-com
【分析】根据三角形三内角之和等于180°求解.
16.如图,在△ABC中,AD与BE相交于点G,若点G是△ABC的重心,则S△AGE:S△GDE= 2:1 .
【分析】根据重心的性质得到AG=2GD,根据三角形的面积公式计算即可.
【解答】解:∵点G是△ABC的重心,
∴AG=2GD,∴S△AGE=2S△GDE,∴S△AGE:S△GDE=2:1,故答案为:2:1.
【点评】本题考查的是三角形重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.
17.(2015秋?淮安校级月考)如图为6个边长相等的正方形的组合图形,则∠1+∠3= 90° .
【分析】首先利用SAS定理判定△ABC≌△DBE,根据全等三角形的性质可得∠3=∠ACB,再由∠ACB+∠1=90°,可得∠1+∠3=90°.www.21-cn-jy.com
【解答】解:∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),∴∠3=∠ACB,
∵∠ACB+∠1=90°,∴∠1+∠3=90°,故答案为:90°.
【点评】此题主要考查了全等图形,关键是掌握全等三角形的判定,以及全等三角形对应角相等.
18.(2014秋?滨湖区期中)如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为 1或4 s.
【分析】由条件分两种情况,当△BPE≌△CQP时,则有BE=PC,由条件可得到关于t的方程,当△BPE≌△CPQ,则有BP=PC,同样可得出t的方程,可求出t的值.
【解答】解:
当△BPE≌△CQP时,则有BE=PC,即14=16﹣2t,解得t=1,
当△BPE≌△CPQ时,则有BP=PC,即2t=16﹣2t,解得t=4,
故答案为:1或4.
【点评】本题主要考查全等三角形的性质,由条件分两种情况得到关于t的方程是解题的关键.
三.解答题(共6小题)
19.(2016?湘桥区一模)如图,在△ABC中,∠C=90°.
(1)用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连结BD,若BD平分∠CBA,求∠A的度数.
【分析】(1)直接利用线段垂直平分线的作法得出即可;
(2)利用线段垂直平分线的性质得出AD=BD,再利用角平分线的性质求出即可.
【解答】解:(1)如图所示,DE为所求作的垂直平分线;
(2)∵DE是AB边上的垂直平分线,
∴AD=BD,∴∠ABD=∠A,
∵BD平分∠CBA,∴∠CBD=∠ABD=∠A,
∵∠C=90°,∴∠CBD+∠ABD+∠A=90°,
∴∠A=30°.
【点评】此题主要考查了基本作图以及线段垂直平分线的性质与作法,熟练掌握线段垂直平分线的性质是解题关键.21教育网
20.(2016春?淮安期中)在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.【来源:21cnj*y.co*m】
【分析】由CD⊥AB与∠B=60°,根据两锐角互余,即可求得∠BCD的度数,又由∠A=20°,∠B=60°,求得∠ACB的度数,由CE是∠ACB的平分线,可求得∠ACE的度数,然后根据三角形外角的性质,求得∠CEB的度数.
【解答】解:∵CD⊥AB,∴∠CDB=90°,
∵∠B=60°,∴∠BCD=90°﹣∠B=90°﹣60°=30°;
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,∴∠ACB=100°,
∵CE是∠ACB的平分线,∴∠ACE=∠ACB=50°,
∴∠CEB=∠A+∠ACE=20°+50°=70°,∠ECD=90°﹣70°=20°
【点评】此题考查了三角形的内角和定理,三角形外角的性质以及三角形高线,角平分线的定义等知识.此题难度不大,解题的关键是数形结合思想的应用.
21.(2015春?安岳县期末)如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°
(1)求线段AE的长.
(2)求∠DFA的度数.
【分析】(1)根据全等三角形的性质解答即可;
(2)根据全等三角形的性质解答即可.
22.(2016?宜宾)如图,已知∠CAB=∠DBA,∠CBD=∠DAC.
求证:BC=AD.
【分析】先根据题意得出∠DAB=∠CBA,再由ASA定理可得出△ADB≌△BCA,由此可得出结论.
【解答】解:∵∠CAB=∠DBA,∠CBD=∠DAC,∴∠DAB=∠CBA.
在△ADB与△BCA中,,∴△ADB≌△BCA(ASA),∴BC=AD.
【点评】本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.
23.(2015?黄冈模拟)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.21*cnjy*com
求证:(1)△BAD≌△CAE;(2)试猜想BD、CE有何特殊位置关系,并证明.
【分析】要证(1)△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由∠BAC=∠DAE=90°很易证得.(2)BD、CE有何特殊位置关系,从图形上可看出是垂直关系,可向这方面努力.要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.【出处:21教育名师】
(2)BD、CE特殊位置关系为BD⊥CE.
证明如下:由(1)知△BAD≌△CAE,∴∠ADB=∠E.
∵∠DAE=90°,∴∠E+∠ADE=90°.∴∠ADB+∠ADE=90°.
即∠BDE=90°.∴BD、CE特殊位置关系为BD⊥CE.
【点评】本题考查了全等三角形的判定和性质;全等问题要注意找条件,有些条件需在图形是仔细观察,认真推敲方可.做题时,有时需要先猜后证.
24.(2016春?太仓市期末)已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则
①∠ABO的度数是 20° ;
②当∠BAD=∠ABD时,x= 120° ;当∠BAD=∠BDA时,x= 60° .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
【分析】利用角平分线的性质求出∠ABO的度数是关键,分类讨论的思想.
【解答】解:(1)①∵∠MON=40°,OE平分∠MON∴∠AOB=∠BON=20°
∵AB∥ON∴∠ABO=20°
②∵∠BAD=∠ABD∴∠BAD=20°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=120°
∵∠BAD=∠BDA,∠ABO=20°∴∠BAD=80°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=60°
故答案为:①20 ②120,60
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=125.
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=20、35、50、125.
【点评】本题考查了三角形的内角和定理和三角形的外角性质的应用,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角之和.21世纪教育网版权所有
一.选择题(共10小题)
1.(2016?岳阳)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm C.3cm,4cm,8cm D.3cm,3cm,4cm
2.(2014?襄阳)下列命题错误的是( )
A.所有的实数都可用数轴上的点表示 B.等角的补角相等
C.无理数包括正无理数,0,负无理数 D.两点之间,线段最短
3.(2015春?普陀区期末)下列说法正确的是( )
A.两个等边三角形一定全等 B.腰对应相等的两个等腰三角形全等
C.形状相同的两个三角形全等 D.全等三角形的面积一定相等
4.(2014秋?新泰)如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
A.∠1=∠2
B.AC=CA
C.∠D=∠B
D.AC=BC
5.(2016?宁波模拟)如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能
判定△ABD≌△BAC的是( )
A.∠D=∠C
B.BD=AC
C.∠CAD=∠DBC
D.AD=BC
6.(2015?台州)某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( ) 21*cnjy*com
A.若甲对,则乙对 B.若乙对,则甲对
C.若乙错,则甲错 D.若甲错,则乙对
7.(2016春?商水)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
8.(2016?资阳)如图,两个三角形的面积分别是9,6,对应阴影部分的面积分别是m,n,则m﹣n等于( )
A.2 B.3
C.4 D.无法确定
9.(2016春?薛城区期中)如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )
A.45° B.55°
C.60° D.75°
(题9图) (题10图)
10.(2016?大埔县一模)已知△ABC中,D,E分别是AC,AB边上的中点,BD⊥CE于点F,CE=2,BD=4,则△ABC的面积为( )
A. B.8 C.4 D.6
二.填空题(共8小题)
11.(2014春?东营区校级期末)一个三角形的三边为2、5、x,另一个三角形的三边
为y、2、6,若这两个三角形全等,则x+y= .
12.(2016?滨湖区一模)对顶角相等的逆命题是 命题(填写“真”或“假”).
13.(2015?齐齐哈尔)如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,
要使△ABC≌△DEF,则只需添加一个适当的条件是 .(只填一个即可)
(题13图) (题14图)
14.(2016?大庆)如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= .
15.(2014?随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 度.
(题15图)
16.如图,在△ABC中,AD与BE相交于点G,若点G是△ABC的重心,
则S△AGE:S△GDE= .
17.(2015秋?淮安校级月考)如图为6个边长相等的正方形的组合图形,
则∠1+∠3= .
18.(2014秋?滨湖区)如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为 s.
(题16图) (题17图) (题18图)
三.解答题(共6小题)
19.(2016?湘桥区一模)如图,在△ABC中,∠C=90°.
(1)用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.
(保留作图痕迹,不要求写作法和证明);
(2)连结BD,若BD平分∠CBA,求∠A的度数.
20.(2016春?淮安期中)在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.【来源:21·世纪·教育·网】
21.(2015春?安岳县期末)如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°2-1-c-n-j-y
(1)求线段AE的长.
(2)求∠DFA的度数.
22.(2016?宜宾)如图,已知∠CAB=∠DBA,∠CBD=∠DAC.求证:BC=AD.
23.(2015?黄冈模拟)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.【版权所有:21教育】
求证:(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
24.(2016春?太仓市期末)已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则
①∠ABO的度数是 ;
②当∠BAD=∠ABD时,x= ;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
浙教版八年级上数学第一章三角形的初步认识单元练习
参考答案与试题解析
一.选择题(共10小题)
1.(2016?岳阳)下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cmB.7cm,4cm,2cmC.3cm,4cm,8cmD.3cm,3cm,4cm
【分析】依据三角形任意两边之和大于第三边求解即可.
【解答】解:A、因为2+3=5,所以不能构成三角形,故A错误;
B、因为2+4<6,所以不能构成三角形,故B错误;
C、因为3+4<8,所以不能构成三角形,故C错误;
D、因为3+3>4,所以能构成三角形,故D正确.故选:D.
【点评】本题主要考查的是三角形的三边关系,掌握三角形的三边关系是解题的关键.
2.(2014?襄阳)下列命题错误的是( )
A.所有的实数都可用数轴上的点表示
B.等角的补角相等
C.无理数包括正无理数,0,负无理数
D.两点之间,线段最短
【点评】本题考查了命题与定理:判断事物的语句叫命题;正确的命题称为真命题,错误的命题称为假命题;经过推理论证的真命题称为定理.21·世纪*教育网
3.(2015春?普陀区期末)下列说法正确的是( )
A.两个等边三角形一定全等
B.腰对应相等的两个等腰三角形全等
C.形状相同的两个三角形全等
D.全等三角形的面积一定相等
【分析】根据全等图形的判定和性质对各个选项进行判断即可.
【解答】解:两个等边三角形边长不一定相等,所以不一定全等,A错误;
腰对应相等的两个等腰三角形对应角不一定相等,所以不一定全等,B错误;
形状相同的两个三角形对应边不一定相等,所以不一定全等,C错误;
全等三角形的面积一定相等,所以D正确,故选:D.
【点评】本题考查的是全等图形的判定和性质,对应角相等、对应边相等的两个图形确定,全等形的周长和面积相等.21·cn·jy·com
4.(2014秋?新泰)如图,△ABC≌△CDA,并且AB=CD,那么下列结论错误的是( )
A.∠1=∠2B.AC=CAC.∠D=∠BD.AC=BC
【分析】由△ABC≌△CDA,并且AB=CD,AC和CA是公共边,可知∠1和∠2,∠D和∠B是对应角.全等三角形的对应角相等,因而前三个选项一定正确.AC和BC不是对应边,不一定相等.2·1·c·n·j·y
【点评】本题主要考查了全等三角形性质;而根据已知条件正确找着对应边、对应角是正确解决本题的关键.
5.(2016?宁波模拟)如图,点C,D在AB同侧,∠CAB=∠DBA,下列条件中不能判定△ABD≌△BAC的是( )
A.∠D=∠CB.BD=ACC.∠CAD=∠DBCD.AD=BC
【分析】根据图形知道隐含条件BC=BC,根据全等三角形的判定定理逐个判断即可.
【解答】解:A、添加条件∠D=∠C,还有已知条件∠CAB=∠DBA,BC=BC,符合全等三角形的判定定理AAS,能推出△ABD≌△BAC,故本选项错误;21cnjy.com
B、添加条件BD=AC,还有已知条件∠CAB=∠DBA,BC=BC,符合全等三角形的判定定理SAS,能推出△ABD≌△BAC,故本选项错误;
C、∵∠CAB=∠DBA,∠CAD=∠DBC,
∴∠DAB=∠CBA,
还有已知条件∠CAB=∠DBA,BC=BC,符合全等三角形的判定定理ASA,能推出△ABD≌△BAC,故本选项错误;
D、添加条件AD=BC,还有已知条件∠CAB=∠DBA,BC=BC,不符合全等三角形的判定定理,不能推出△ABD≌△BAC,故本选项正确;故选D.
【点评】本题考查了全等三角形的判定定理的应用,能熟记全等三角形的判定定理是解此题的关键,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,符合SSA和AAA不能推出两三角形全等.
6.(2015?台州)某班有20位同学参加围棋、象棋比赛,甲说:“只参加一项的人数大于14人.”乙说:“两项都参加的人数小于5.”对于甲、乙两人的说法,有下列四个命题,其中真命题的是( )
A.若甲对,则乙对B.若乙对,则甲对C.若乙错,则甲错D.若甲错,则乙对
【分析】分别假设甲说的对和乙说的正确,进而得出答案.
【解答】解:若甲对,即只参加一项的人数大于14人,假设只参加一项的人数是15人,
则两项都参加的人数为5人,故乙错.
若乙对,即两项都参加的人数小于5人,则两项都参加的人数至多为4人,
此时只参加一项的人数为16人,故甲对.故选:B.
【点评】此题主要考查了推理与论证,关键是分两种情况分别进行分析.
7.(2016春?商水)如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
【分析】根据全等三角形对应边相等,全等三角形对应角相等结合图象解答即可.
【解答】解:∵△ABC≌△AEF,
∴AC=AF,故①正确;∠EAF=∠BAC,
∴∠FAC=∠EAB≠∠FAB,故②错误;EF=BC,故③正确;
∠EAB=∠FAC,故④正确;综上所述,结论正确的是①③④共3个.故选C.
【点评】本题考查了全等三角形的性质,熟记性质并准确识图,准确确定出对应边和对应角是解题的关键.
【分析】设空白出的面积为x,根据题意列出关系式,相减即可求出m﹣n的值.
【解答】解:设空白出图形的面积为x,
根据题意得:m+x=9,n+x=6,则m﹣n=9﹣6=3.故选B.
【点评】本题考查了三角形的面积;设出未知数,根据三角形的面积得出关系式是解决问题的关键.
9.(2016春?薛城区期中)如图,已知等边△ABC中,BD=CE,AD与BE相交于点P,则∠BPD的度数为( )21教育名师原创作品
A.45°B.55°
C.60°D.75°
【分析】根据等边三角形性质得出∠ABD=∠C=60°,AB=BC,证出△ABD≌△BCE,根据全等三角形的性质得出∠BAD=∠CBE,根据三角形外角性质得出∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC,即可得出答案.
【解答】解:∵△ABC是等边三角形,∴∠ABD=∠C=60°,AB=BC,
在△ABD和△BCE中,,∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,∴∠BPD=∠ABE+∠BAD=∠ABE+∠CBE=∠ABC=60°.故选C.
【点评】本题考查了等边三角形的性质,全等三角形的性质和判定,三角形外角性质的应用,解此题的关键是求出△ABD≌△BCE.
【分析】连接ED,根据三角形中位线定理证明△ADE∽△ABC,且相似比为1:2,求出四边形EBCD的面积,根据相似三角形的面积比等于相似比的平方列式计算即可.
【解答】解:连接ED,
∵BD⊥CE,∴四边形EBCD的面积=×BD×CE=4,设△ABC的面积为x,
∵D,E分别是AC,AB边上的中点,∴BC=2DE,ED∥BC,∴△ADE∽△ABC,
△ABC的面积=4×△ADE的面积,即x=4(x﹣4),解得x=.故选:A.
【点评】本题考查的是三角形的中位线的性质和相似三角形的判定和性质,掌握三角形的中位线定理和相似三角形的性质定理是解题的关键.
二.填空题(共8小题)
11.(2014春?东营区校级期末)一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y= 11 .
【分析】根据已知条件分清对应边,结合全的三角形的性质可得出答案.
【解答】解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5∴x+y=11.故填11.
【点评】本题考查了全等三角形的性质及对应边的找法;根据两个三角形中都有2找对对应边是解决本题的关键.
12.(2016?滨湖区一模)对顶角相等的逆命题是 假 命题(填写“真”或“假”).
【分析】先根据互逆命题的定义写出对顶角相等的逆命题,再判断真假.
【解答】解:“对顶角相等”的逆命题是:相等的角是对顶角,它是假命题.故答案为:假.
【点评】本题考查了互逆命题及真假命题的定义.两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题;正确的命题叫做真命题,错误的命题叫做假命题.
13.(2015?齐齐哈尔)如图,点B、A、D、E在同一直线上,BD=AE,BC∥EF,要使△ABC≌△DEF,则只需添加一个适当的条件是 BC=EF或∠BAC=∠EDF .(只填一个即可)
【分析】BC=EF或∠BAC=∠EDF,若BC=EF,根据条件利用SAS即可得证;若∠BAC=∠EDF,根据条件利用ASA即可得证.
在△ABC和△DEF中,,∴△ABC≌△DEF(SAS);
若添加∠BAC=∠EDF,∵BC∥EF,∴∠B=∠E,
∵BD=AE,∴BD﹣AD=AE﹣AD,即BA=ED,
在△ABC和△DEF中,,∴△ABC≌△DEF(ASA),
故答案为:BC=EF或∠BAC=∠EDF
【点评】此题考查了全等三角形的判定,熟练掌握全等三角形的判定方法是解本题的关键.
14.(2016?大庆)如图,在△ABC中,∠A=40°,D点是∠ABC和∠ACB角平分线的交点,则∠BDC= 110° .
【分析】由D点是∠ABC和∠ACB角平分线的交点可推出∠DBC+∠DCB=70,再利用三角形内角和定理即可求出∠BDC的度数.
【解答】解:∵D点是∠ABC和∠ACB角平分线的交点,
∴有∠CBD=∠ABD=∠ABC,∠BCD=∠ACD=∠ACB,
∴∠ABC+∠ACB=180﹣40=140,∴∠OBC+∠OCB=70,∴∠BOC=180﹣70=110°,
故答案为:110°.
【点评】此题主要考查学生对角平分线性质,三角形内角和定理,三角形的外角性质等知识点的理解和掌握,难度不大,是一道基础题,熟记三角形内角和定理是解决问题的关键.
15.(2014?随州)将一副直角三角板如图放置,使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合,则∠1的度数为 75 度.www-2-1-cnjy-com
【分析】根据三角形三内角之和等于180°求解.
16.如图,在△ABC中,AD与BE相交于点G,若点G是△ABC的重心,则S△AGE:S△GDE= 2:1 .
【分析】根据重心的性质得到AG=2GD,根据三角形的面积公式计算即可.
【解答】解:∵点G是△ABC的重心,
∴AG=2GD,∴S△AGE=2S△GDE,∴S△AGE:S△GDE=2:1,故答案为:2:1.
【点评】本题考查的是三角形重心的概念和性质:三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍.
17.(2015秋?淮安校级月考)如图为6个边长相等的正方形的组合图形,则∠1+∠3= 90° .
【分析】首先利用SAS定理判定△ABC≌△DBE,根据全等三角形的性质可得∠3=∠ACB,再由∠ACB+∠1=90°,可得∠1+∠3=90°.www.21-cn-jy.com
【解答】解:∵在△ABC和△DBE中,
∴△ABC≌△DBE(SAS),∴∠3=∠ACB,
∵∠ACB+∠1=90°,∴∠1+∠3=90°,故答案为:90°.
【点评】此题主要考查了全等图形,关键是掌握全等三角形的判定,以及全等三角形对应角相等.
18.(2014秋?滨湖区期中)如图,已知长方形ABCD的边长AB=20cm,BC=16cm,点E在边AB上,AE=6cm,如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动,同时,点Q在线段CD上从点C到点D运动.则当△BPE与△CQP全等时,时间t为 1或4 s.
【分析】由条件分两种情况,当△BPE≌△CQP时,则有BE=PC,由条件可得到关于t的方程,当△BPE≌△CPQ,则有BP=PC,同样可得出t的方程,可求出t的值.
【解答】解:
当△BPE≌△CQP时,则有BE=PC,即14=16﹣2t,解得t=1,
当△BPE≌△CPQ时,则有BP=PC,即2t=16﹣2t,解得t=4,
故答案为:1或4.
【点评】本题主要考查全等三角形的性质,由条件分两种情况得到关于t的方程是解题的关键.
三.解答题(共6小题)
19.(2016?湘桥区一模)如图,在△ABC中,∠C=90°.
(1)用尺规作图法作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)连结BD,若BD平分∠CBA,求∠A的度数.
【分析】(1)直接利用线段垂直平分线的作法得出即可;
(2)利用线段垂直平分线的性质得出AD=BD,再利用角平分线的性质求出即可.
【解答】解:(1)如图所示,DE为所求作的垂直平分线;
(2)∵DE是AB边上的垂直平分线,
∴AD=BD,∴∠ABD=∠A,
∵BD平分∠CBA,∴∠CBD=∠ABD=∠A,
∵∠C=90°,∴∠CBD+∠ABD+∠A=90°,
∴∠A=30°.
【点评】此题主要考查了基本作图以及线段垂直平分线的性质与作法,熟练掌握线段垂直平分线的性质是解题关键.21教育网
20.(2016春?淮安期中)在△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.求∠BCD和∠ECD的度数.【来源:21cnj*y.co*m】
【分析】由CD⊥AB与∠B=60°,根据两锐角互余,即可求得∠BCD的度数,又由∠A=20°,∠B=60°,求得∠ACB的度数,由CE是∠ACB的平分线,可求得∠ACE的度数,然后根据三角形外角的性质,求得∠CEB的度数.
【解答】解:∵CD⊥AB,∴∠CDB=90°,
∵∠B=60°,∴∠BCD=90°﹣∠B=90°﹣60°=30°;
∵∠A=20°,∠B=60°,∠A+∠B+∠ACB=180°,∴∠ACB=100°,
∵CE是∠ACB的平分线,∴∠ACE=∠ACB=50°,
∴∠CEB=∠A+∠ACE=20°+50°=70°,∠ECD=90°﹣70°=20°
【点评】此题考查了三角形的内角和定理,三角形外角的性质以及三角形高线,角平分线的定义等知识.此题难度不大,解题的关键是数形结合思想的应用.
21.(2015春?安岳县期末)如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°
(1)求线段AE的长.
(2)求∠DFA的度数.
【分析】(1)根据全等三角形的性质解答即可;
(2)根据全等三角形的性质解答即可.
22.(2016?宜宾)如图,已知∠CAB=∠DBA,∠CBD=∠DAC.
求证:BC=AD.
【分析】先根据题意得出∠DAB=∠CBA,再由ASA定理可得出△ADB≌△BCA,由此可得出结论.
【解答】解:∵∠CAB=∠DBA,∠CBD=∠DAC,∴∠DAB=∠CBA.
在△ADB与△BCA中,,∴△ADB≌△BCA(ASA),∴BC=AD.
【点评】本题考查的是全等三角形的判定与性质,熟知全等三角形的判定定理是解答此题的关键.
23.(2015?黄冈模拟)已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.21*cnjy*com
求证:(1)△BAD≌△CAE;(2)试猜想BD、CE有何特殊位置关系,并证明.
【分析】要证(1)△BAD≌△CAE,现有AB=AC,AD=AE,需它们的夹角∠BAD=∠CAE,而由∠BAC=∠DAE=90°很易证得.(2)BD、CE有何特殊位置关系,从图形上可看出是垂直关系,可向这方面努力.要证BD⊥CE,需证∠BDE=90°,需证∠ADB+∠ADE=90°可由直角三角形提供.【出处:21教育名师】
(2)BD、CE特殊位置关系为BD⊥CE.
证明如下:由(1)知△BAD≌△CAE,∴∠ADB=∠E.
∵∠DAE=90°,∴∠E+∠ADE=90°.∴∠ADB+∠ADE=90°.
即∠BDE=90°.∴BD、CE特殊位置关系为BD⊥CE.
【点评】本题考查了全等三角形的判定和性质;全等问题要注意找条件,有些条件需在图形是仔细观察,认真推敲方可.做题时,有时需要先猜后证.
24.(2016春?太仓市期末)已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则
①∠ABO的度数是 20° ;
②当∠BAD=∠ABD时,x= 120° ;当∠BAD=∠BDA时,x= 60° .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
【分析】利用角平分线的性质求出∠ABO的度数是关键,分类讨论的思想.
【解答】解:(1)①∵∠MON=40°,OE平分∠MON∴∠AOB=∠BON=20°
∵AB∥ON∴∠ABO=20°
②∵∠BAD=∠ABD∴∠BAD=20°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=120°
∵∠BAD=∠BDA,∠ABO=20°∴∠BAD=80°∵∠AOB+∠ABO+∠OAB=180°∴∠OAC=60°
故答案为:①20 ②120,60
②当点D在射线BE上时,因为∠ABE=110°,且三角形的内角和为180°,
所以只有∠BAD=∠BDA,此时x=125.
综上可知,存在这样的x的值,使得△ADB中有两个相等的角,
且x=20、35、50、125.
【点评】本题考查了三角形的内角和定理和三角形的外角性质的应用,注意:三角形的内角和等于180°,三角形的一个外角等于和它不相邻的两个内角之和.21世纪教育网版权所有
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
