2.6.1直角三角形 学案

中小学教育资源及组卷应用平台
学习任务单
课程基本信息
学科 数学 年级 八年级 学期 上学期
课题 2.6.1直角三角形
教科书 书 名：义务教育教科书数学八年级上册 出版社：浙江教育出版社
学生信息
姓名 学校 班级 学号
学习目标
理解直角三角形的概念； 2.掌握直角三角形的性质，并能运用．
课前学习任务
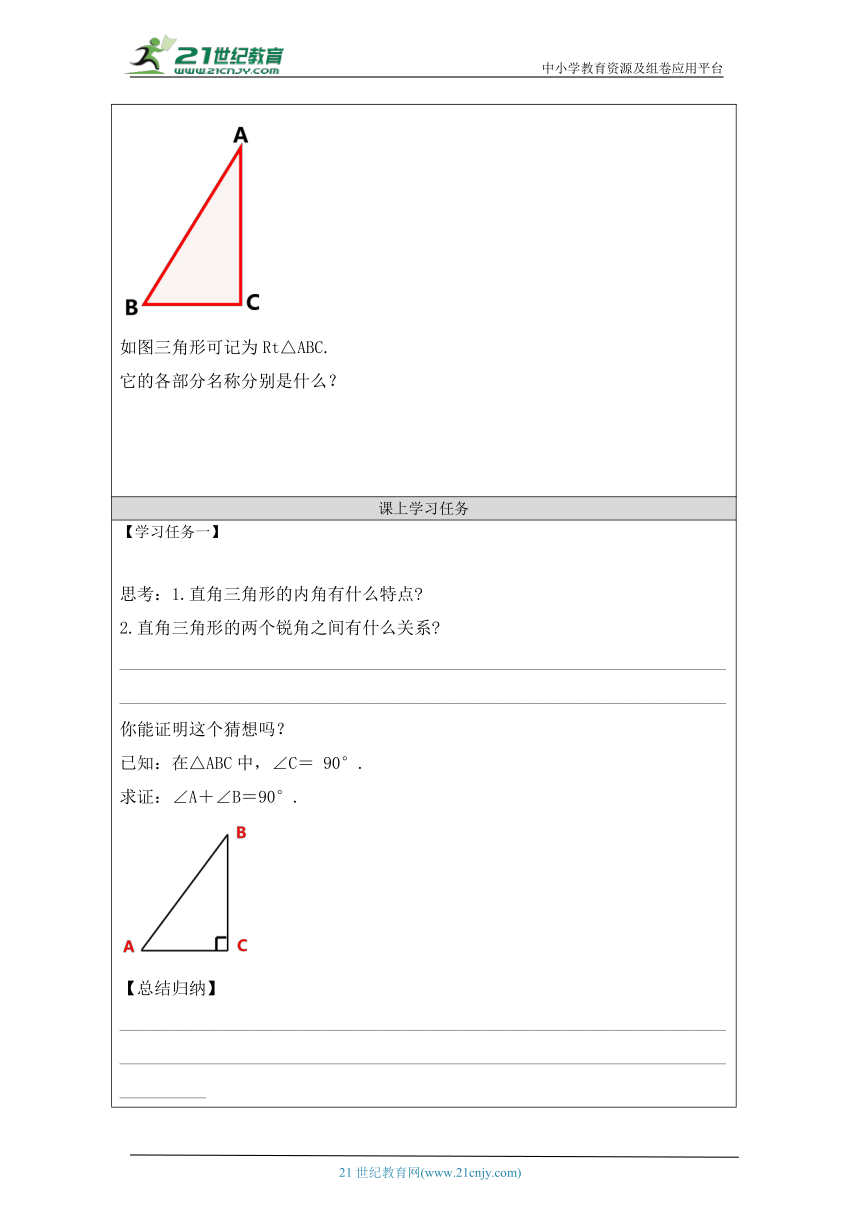
复习引入 什么样的三角形叫做直角三角形？ 日常生活中常见的直角三角形有哪些 直角三角形的表示方法。 直角三角形可以用符号“Rt△”表示。 如图三角形可记为Rt△ABC. 它的各部分名称分别是什么？
课上学习任务
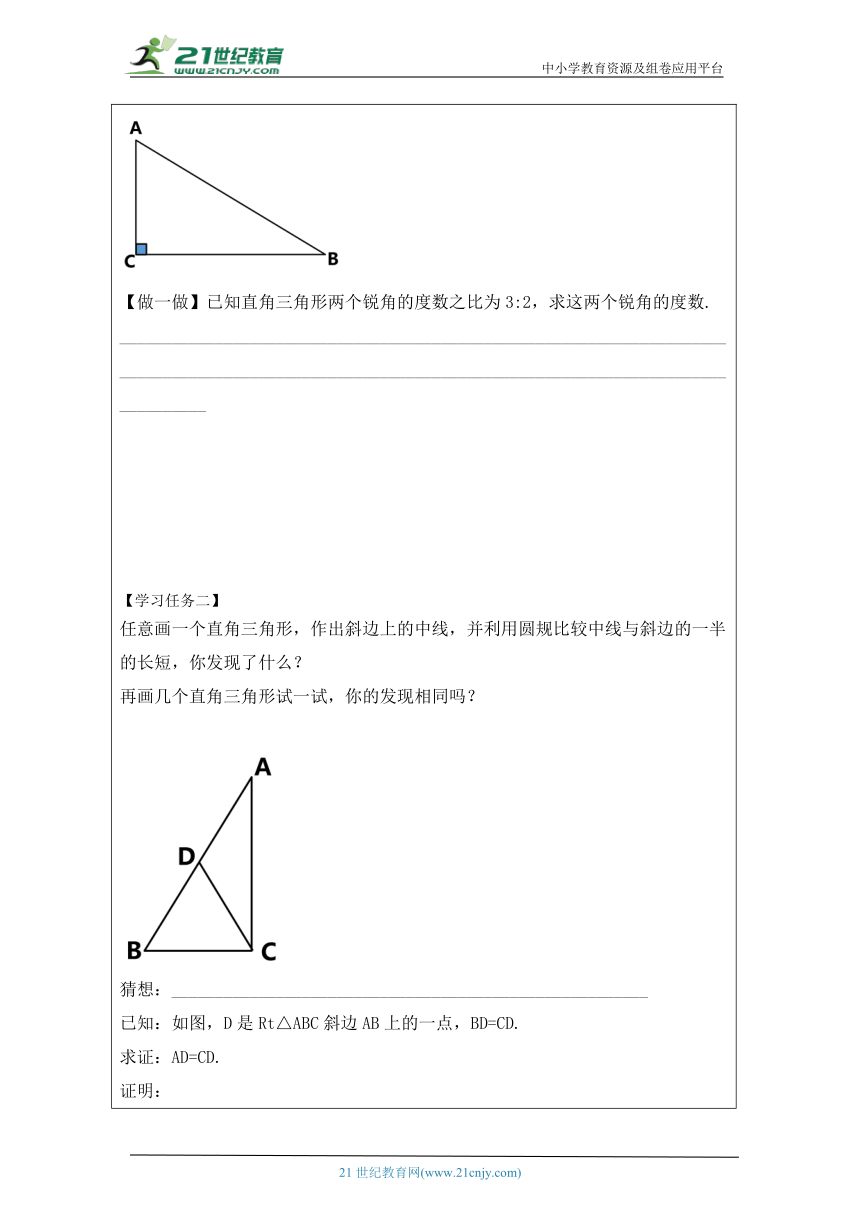
【学习任务一】 思考：1.直角三角形的内角有什么特点 2.直角三角形的两个锐角之间有什么关系 ____________________________________________________________________________________________________________________________________________ 你能证明这个猜想吗？ 已知：在△ABC中，∠C＝ 90°. 求证：∠A＋∠B＝90°. 【总结归纳】 ______________________________________________________________________________________________________________________________________________________ 【做一做】已知直角三角形两个锐角的度数之比为3:2，求这两个锐角的度数. ______________________________________________________________________________________________________________________________________________________ 【学习任务二】 任意画一个直角三角形，作出斜边上的中线，并利用圆规比较中线与斜边的一半的长短，你发现了什么？ 再画几个直角三角形试一试，你的发现相同吗？ 猜想：_______________________________________________________ 已知：如图，D是Rt△ABC斜边AB上的一点，BD=CD. 求证：AD=CD. 证明： ________________________________________________________________________________________________________________________________________________________________________________________________________________________________ 直角三角形的性质2： ______________________________________________________________ 用数学语言表述为： ________________________________________________________________________________________________________________________________________________________________________________________________________________________________ 【学习任务三】 例1 如图，一名滑雪运动员沿着倾斜角为30°的斜坡，从A滑行至B.已知AB＝200m，问这名滑雪运动员的高度下降了多少米？ 解： ________________________________________________________________________________________________________________________________________________________________________________________________________________________________ 【学习任务四】课堂练习 必做题： 1.如图，公路AC，BC互相垂直，公路AB的中点M与点C被湖隔开，若测得AM的长为1.2 km，则M，C两点间的距离为(　　) A．0.5 km B．0.6 km C．0.9 km D．1.2 km 2.如图，在Rt△ACB中，∠ACB＝90°，CD为AB边上的中线， ∠A＝30°. 若CD＝6，则BC的长度为(　　) A．2 B．4 C．6 D．8 选做题： 3.如图，在△ACB中，∠ACB＝90°，CD⊥AB于D. (1)求证：∠ACD＝∠B； (2)若AF平分∠CAB分别交CD，BC于E，F，求证：∠CEF＝∠CFE. 【综合拓展类作业】 4.在四边形ABCD中，∠ABC＝∠ADC＝90°，M，N分别是AC，BD的中点，猜一猜MN与BD的位置关系，再证明你的结论． 【知识技能类作业】 必做题： 1.如图，某社会实践学习小组为测量学校A与河对岸江景房B之间的距离，在学校附近选一点C，利用测量仪器测得∠A＝60°，∠C＝90°，AC＝30米．由此可求得学校与江景房之间的距离AB等于（　　） A．15米 B．60米 C．80米 D．120米 选做题： 在四边形ABCD中，∠ABC＝∠ADC＝90°，M，N分别是AC，BD的中点，猜一猜MN与BD的位置关系，再证明你的结论． 【综合拓展类作业】 3.用一副三角尺拼出甲、乙两个图形，求: 图中,∠ABD的度数. 图中,∠DCF，∠CFD,∠AEF的度数.
21世纪教育网(www.21cnjy.com)