2.7.1探索勾股定理 课件(共30张PPT)
文档属性
| 名称 | 2.7.1探索勾股定理 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 09:03:34 | ||
图片预览






文档简介
(共30张PPT)
第二章 特殊三角形
2.7.1探索勾股定理
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.了解拼图验证勾股定理的方法;
2.掌握勾股定理,会利用两边边长求直角三角形的另一边长;
3.会利用勾股定理解决实际问题.
02
新知导入
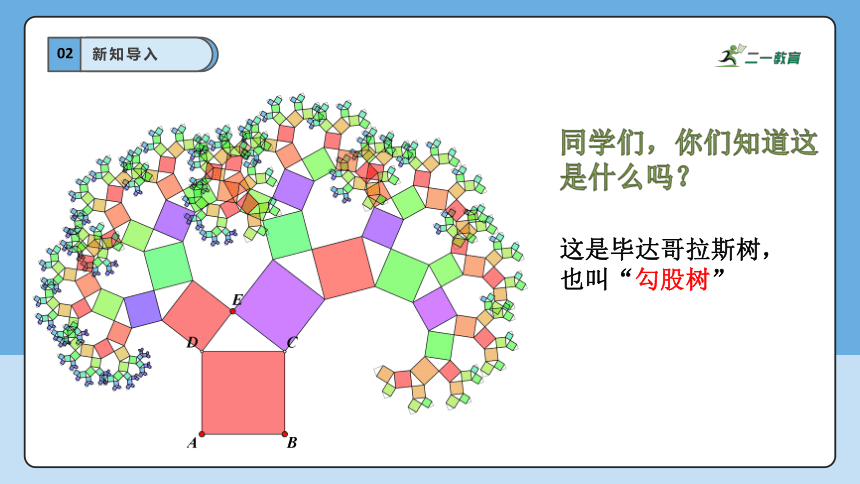
同学们,你们知道这是什么吗?
这是毕达哥拉斯树,也叫“勾股树”
03
新知探究
这节课我们就一起来探索“勾股树”所蕴含的数学知识——勾股定理,体验数学文化之美。
03
新知探究
合作学习
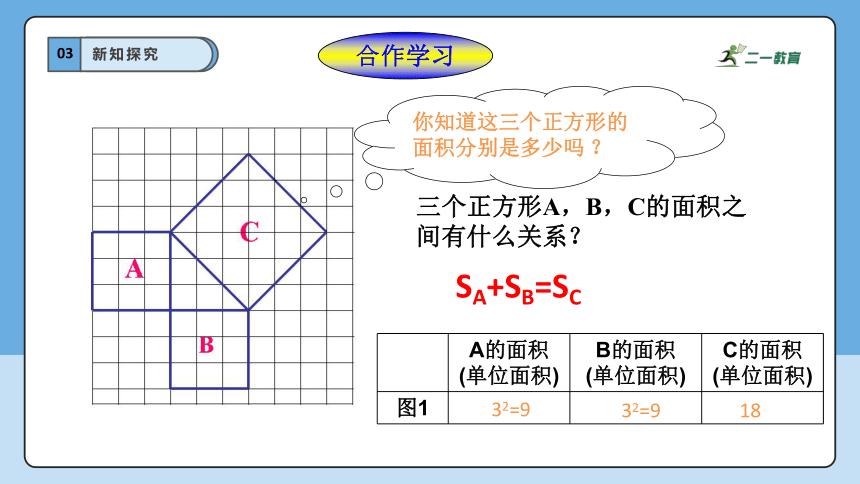
你知道这三个正方形的面积分别是多少吗 ?
三个正方形A,B,C的面积之间有什么关系?
SA+SB=SC
A的面积 (单位面积) B的面积 (单位面积) C的面积
(单位面积)
图1
32=9
32=9
18
03
新知讲解
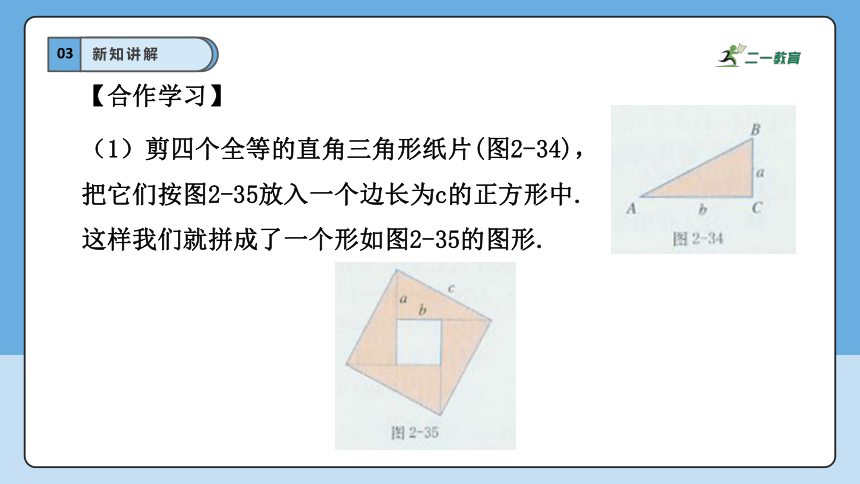
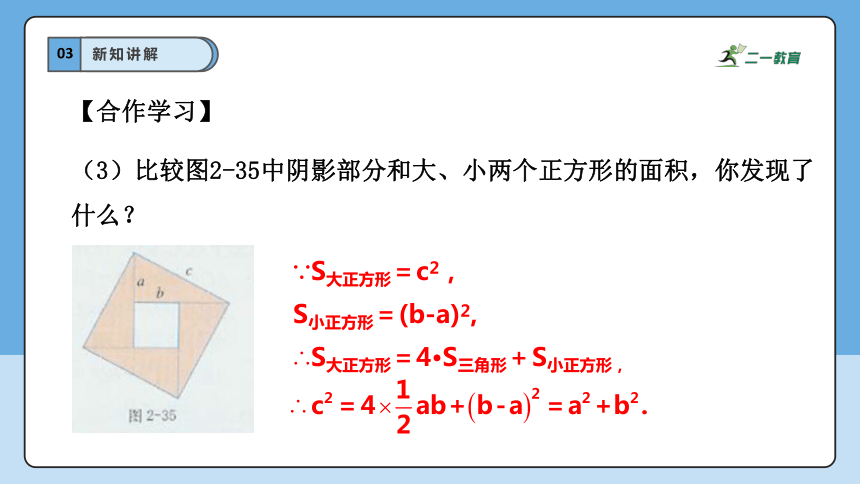
(1)剪四个全等的直角三角形纸片(图2-34),把它们按图2-35放入一个边长为c的正方形中.
这样我们就拼成了一个形如图2-35的图形.
【合作学习】
03
新知讲解
(2)设剪出的直角三角形纸片的两条直角边长分别为a,b,斜边长为c.分别计算图2-35中的阴影部分的面积和大、小两个正方形的面积.
S大正方形=c2,
S小正方形=(b-a)2,
【合作学习】
S阴影=
03
新知讲解
(3)比较图2-35中阴影部分和大、小两个正方形的面积,你发现了什么?
【合作学习】
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
03
新知讲解
如图是在北京召开的第24届国际数学家大会(ICM- 2002 )的会标,它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图。用弦图证明勾股定理在数学史上有着重要的地位.
03
新知讲解
提炼概念
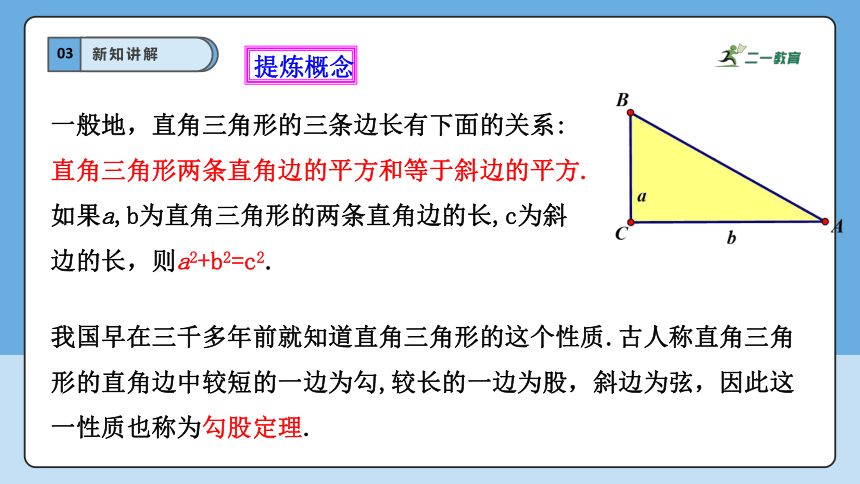
一般地,直角三角形的三条边长有下面的关系:
直角三角形两条直角边的平方和等于斜边的平方.
如果a,b为直角三角形的两条直角边的长,c为斜边的长,则a2+b2=c2.
我国早在三千多年前就知道直角三角形的这个性质.古人称直角三角形的直角边中较短的一边为勾,较长的一边为股,斜边为弦,因此这一性质也称为勾股定理.
03
新知讲解
【拓展延伸】
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
03
新知讲解
方法 图形 证明
“赵爽弦图”
勾股定理的多种证法
03
新知讲解
方法 图形 证明
刘徽“青朱出入图”
加菲尔德总统拼图
03
新知讲解
方法 图形 证明
毕达哥拉斯拼图
古印度的“无字证明”,单靠移动几个图形就直观地验证了勾股定理
03
新知讲解
例1
已知在△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=c
(1)若 a=1, b=2, 求c;
(2)若 a=15, c=17, 求b.
c2=a2+b2=12 +22 =5
∵c>0,
解:(1)根据勾股定理,得
∴c=
(2)根据勾股定理,得
∵b>0 , ∴b=8.
=172 -152
=64.
=(17+15)(17-15)
b2 = c2 -a2
03
新知讲解
如图,这是一个长方形零件图.根据所给的尺寸(单位:mm),求两孔中心A,B之间的距离.
分析:解决问题的关键是构造出含所求线段的直角三角形,然后用勾股定理求解.
例2
03
新知讲解
例2.如图,这是一个长方形零件图.根据所给的尺寸(单位:mm),求两孔中心A,B之间的距离.
解:过A作铅垂线,过B作水平线,两线交于点C,则∠ACB=90°,AC=90- 40= 50( mm),
BC= 160- 40= 120( mm).
由勾股定理,得AB2=AC2+ BC2= 502+ 1202= 16 900( mm2).
∵ AB>0,∴AB= 130(mm).
答:两孔中心A,B之间的距离为130 mm.
03
新知讲解
利用勾股定理求直角三角形的边长的方法:
一般都要经过“一分二代三化简”这“三步曲”,即
一分:分清哪条边是斜边,哪些是直角边;
二代:将已知边长及两边之间的关系式代入a2+b2=c2(假设c是斜边);
三化简.
【总结提升】
04
课堂练习
【知识技能类作业】必做题:
1.如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是 ( )
C
A.12 B.13 C.144 D.194
04
课堂练习
【知识技能类作业】选做题:
2.在直角三角形中,已知其中两边分别为3和4,则第三边等于__________.
04
课堂练习
【综合拓展类作业】
3.在△ABC中,∠C=Rt∠,AB=c,BC=a,AC=b.
(1)如果a= 9,b=12,求c.
(2)如果a=12,c=13,求b.
(3)如果c=34,a:b=8:15,求a,b.
解: ∵在△ABC中,∠C=Rt∠,AB=c,BC=a,AC=b.
∴ a2+b2=c2
(1)∵c2=a2+b2=92+122=225 又∵c>0 ∴c=15
04
课堂练习
【综合拓展类作业】
解: (2)∵ b2=c2-a2=132-122=25
又∵b>0
∴b=5
(3)设a=8x,则b=15x
∴64x2+225x2=342
∴x=2
则a=8x=16,b=15x=30
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1.如图,在△ABC中,AD⊥BC于D,AB=17,BD=15,DC=6,则AC的长为( )
A.11 B.10 C.9 D.8
B
06
作业布置
【知识技能类作业】选做题:
2.我国古代的数学家很早就发现并应用勾股定理,而且尝试对勾股定理做出证明.最早对勾股定理进行证明的是三国时期吴国的数学家赵爽.如图,就是著名的“赵爽弦图”.△ABE,△BCF,△CDG和△DAH是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.已知AB=5, AH=3,求EF的长.小敏的思路是设EF=x,根据题意,小敏所列的方程是 .
32+(x+3)2=52
06
作业布置
【综合拓展类作业】
(1)求墙的高度
解:
∴AC=
∵∠ACB=90°AB=3,BC=1
=
=
(2)若梯子的顶端下滑0.5米,
底端将向外水平移动多少米
A
A′
B
B′
3m
1m
C
∴ AB2=AC2+BC2
3. 有一架3米长的梯子靠在学校围墙上,刚好与墙头对齐,此时梯脚B与墙脚C的距离是1米。
06
作业布置
【综合拓展类作业】
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第二章 特殊三角形
2.7.1探索勾股定理
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.了解拼图验证勾股定理的方法;
2.掌握勾股定理,会利用两边边长求直角三角形的另一边长;
3.会利用勾股定理解决实际问题.
02
新知导入
同学们,你们知道这是什么吗?
这是毕达哥拉斯树,也叫“勾股树”
03
新知探究
这节课我们就一起来探索“勾股树”所蕴含的数学知识——勾股定理,体验数学文化之美。
03
新知探究
合作学习
你知道这三个正方形的面积分别是多少吗 ?
三个正方形A,B,C的面积之间有什么关系?
SA+SB=SC
A的面积 (单位面积) B的面积 (单位面积) C的面积
(单位面积)
图1
32=9
32=9
18
03
新知讲解
(1)剪四个全等的直角三角形纸片(图2-34),把它们按图2-35放入一个边长为c的正方形中.
这样我们就拼成了一个形如图2-35的图形.
【合作学习】
03
新知讲解
(2)设剪出的直角三角形纸片的两条直角边长分别为a,b,斜边长为c.分别计算图2-35中的阴影部分的面积和大、小两个正方形的面积.
S大正方形=c2,
S小正方形=(b-a)2,
【合作学习】
S阴影=
03
新知讲解
(3)比较图2-35中阴影部分和大、小两个正方形的面积,你发现了什么?
【合作学习】
∵S大正方形=c2,
S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
03
新知讲解
如图是在北京召开的第24届国际数学家大会(ICM- 2002 )的会标,它的设计思路可追溯到3世纪中国数学家赵爽所使用的弦图。用弦图证明勾股定理在数学史上有着重要的地位.
03
新知讲解
提炼概念
一般地,直角三角形的三条边长有下面的关系:
直角三角形两条直角边的平方和等于斜边的平方.
如果a,b为直角三角形的两条直角边的长,c为斜边的长,则a2+b2=c2.
我国早在三千多年前就知道直角三角形的这个性质.古人称直角三角形的直角边中较短的一边为勾,较长的一边为股,斜边为弦,因此这一性质也称为勾股定理.
03
新知讲解
【拓展延伸】
在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.
勾
股
03
新知讲解
方法 图形 证明
“赵爽弦图”
勾股定理的多种证法
03
新知讲解
方法 图形 证明
刘徽“青朱出入图”
加菲尔德总统拼图
03
新知讲解
方法 图形 证明
毕达哥拉斯拼图
古印度的“无字证明”,单靠移动几个图形就直观地验证了勾股定理
03
新知讲解
例1
已知在△ABC中, ∠C=Rt∠,BC=a,AC=b,AB=c
(1)若 a=1, b=2, 求c;
(2)若 a=15, c=17, 求b.
c2=a2+b2=12 +22 =5
∵c>0,
解:(1)根据勾股定理,得
∴c=
(2)根据勾股定理,得
∵b>0 , ∴b=8.
=172 -152
=64.
=(17+15)(17-15)
b2 = c2 -a2
03
新知讲解
如图,这是一个长方形零件图.根据所给的尺寸(单位:mm),求两孔中心A,B之间的距离.
分析:解决问题的关键是构造出含所求线段的直角三角形,然后用勾股定理求解.
例2
03
新知讲解
例2.如图,这是一个长方形零件图.根据所给的尺寸(单位:mm),求两孔中心A,B之间的距离.
解:过A作铅垂线,过B作水平线,两线交于点C,则∠ACB=90°,AC=90- 40= 50( mm),
BC= 160- 40= 120( mm).
由勾股定理,得AB2=AC2+ BC2= 502+ 1202= 16 900( mm2).
∵ AB>0,∴AB= 130(mm).
答:两孔中心A,B之间的距离为130 mm.
03
新知讲解
利用勾股定理求直角三角形的边长的方法:
一般都要经过“一分二代三化简”这“三步曲”,即
一分:分清哪条边是斜边,哪些是直角边;
二代:将已知边长及两边之间的关系式代入a2+b2=c2(假设c是斜边);
三化简.
【总结提升】
04
课堂练习
【知识技能类作业】必做题:
1.如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的面积是 ( )
C
A.12 B.13 C.144 D.194
04
课堂练习
【知识技能类作业】选做题:
2.在直角三角形中,已知其中两边分别为3和4,则第三边等于__________.
04
课堂练习
【综合拓展类作业】
3.在△ABC中,∠C=Rt∠,AB=c,BC=a,AC=b.
(1)如果a= 9,b=12,求c.
(2)如果a=12,c=13,求b.
(3)如果c=34,a:b=8:15,求a,b.
解: ∵在△ABC中,∠C=Rt∠,AB=c,BC=a,AC=b.
∴ a2+b2=c2
(1)∵c2=a2+b2=92+122=225 又∵c>0 ∴c=15
04
课堂练习
【综合拓展类作业】
解: (2)∵ b2=c2-a2=132-122=25
又∵b>0
∴b=5
(3)设a=8x,则b=15x
∴64x2+225x2=342
∴x=2
则a=8x=16,b=15x=30
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1.如图,在△ABC中,AD⊥BC于D,AB=17,BD=15,DC=6,则AC的长为( )
A.11 B.10 C.9 D.8
B
06
作业布置
【知识技能类作业】选做题:
2.我国古代的数学家很早就发现并应用勾股定理,而且尝试对勾股定理做出证明.最早对勾股定理进行证明的是三国时期吴国的数学家赵爽.如图,就是著名的“赵爽弦图”.△ABE,△BCF,△CDG和△DAH是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.已知AB=5, AH=3,求EF的长.小敏的思路是设EF=x,根据题意,小敏所列的方程是 .
32+(x+3)2=52
06
作业布置
【综合拓展类作业】
(1)求墙的高度
解:
∴AC=
∵∠ACB=90°AB=3,BC=1
=
=
(2)若梯子的顶端下滑0.5米,
底端将向外水平移动多少米
A
A′
B
B′
3m
1m
C
∴ AB2=AC2+BC2
3. 有一架3米长的梯子靠在学校围墙上,刚好与墙头对齐,此时梯脚B与墙脚C的距离是1米。
06
作业布置
【综合拓展类作业】
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
