2.8直角三角形全等的判定 课件(共29张PPT)
文档属性
| 名称 | 2.8直角三角形全等的判定 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-28 09:03:58 | ||
图片预览




文档简介
(共29张PPT)
第二章 特殊三角形
2.8直角三角形全等的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1、探索两个直角三角形全等的条件.
2、握两个直角三角形全等的条件(HL).
3、了解角平分线的性质:角的内部,到角两边距离相等的点,在角平分线上,及其简单应用. 探
02
新知导入
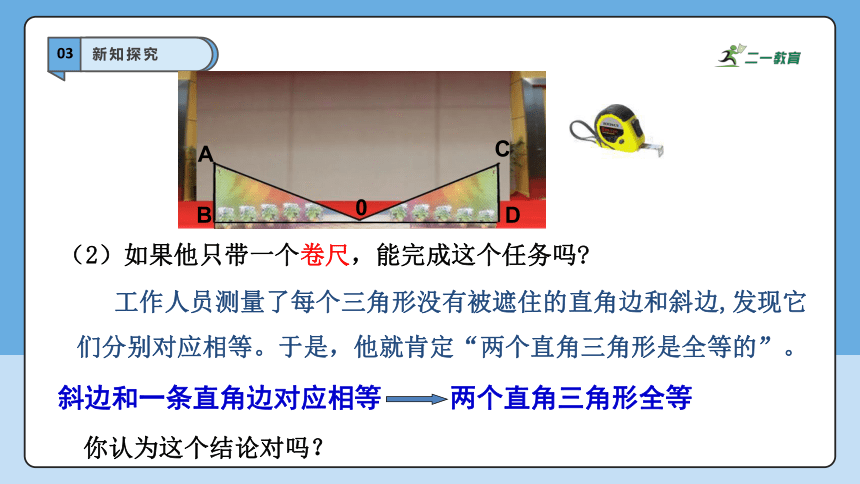
舞台背景的形状是两个直角三角形,工作人员带了量角器和卷尺。如果他想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量。
(1) 你能帮他想个办法吗?
生活中的数学
A
C
0
03
新知探究
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等。于是,他就肯定“两个直角三角形是全等的”。
你认为这个结论对吗?
(2)如果他只带一个卷尺,能完成这个任务吗
斜边和一条直角边对应相等 两个直角三角形全等
A
B
C
D
0
03
新知探究
合作学习
三角形全等的判定
定义:
基本事实:
AAS
证得
复习回顾
能够重合的两个三角形是全等三角形
SSS SAS ASA
03
新知讲解
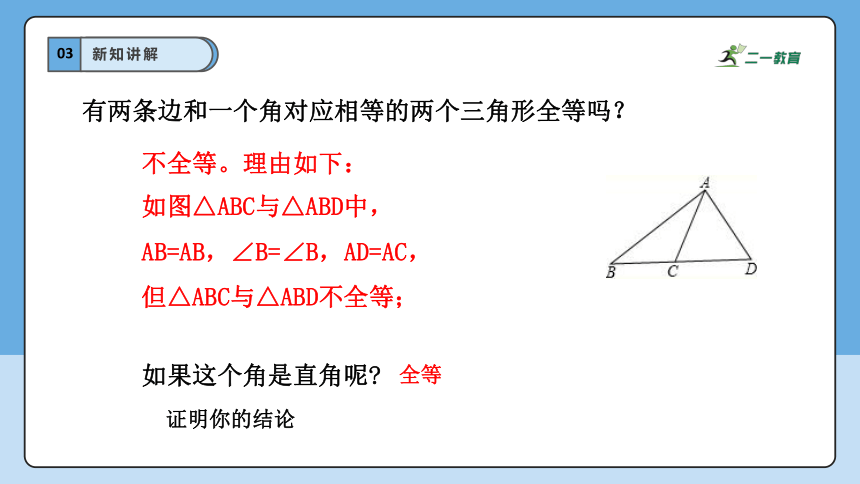
有两条边和一个角对应相等的两个三角形全等吗?
不全等。理由如下:
如果这个角是直角呢
如图△ABC与△ABD中,
AB=AB,∠B=∠B,AD=AC,
但△ABC与△ABD不全等;
全等
证明你的结论
03
新知讲解
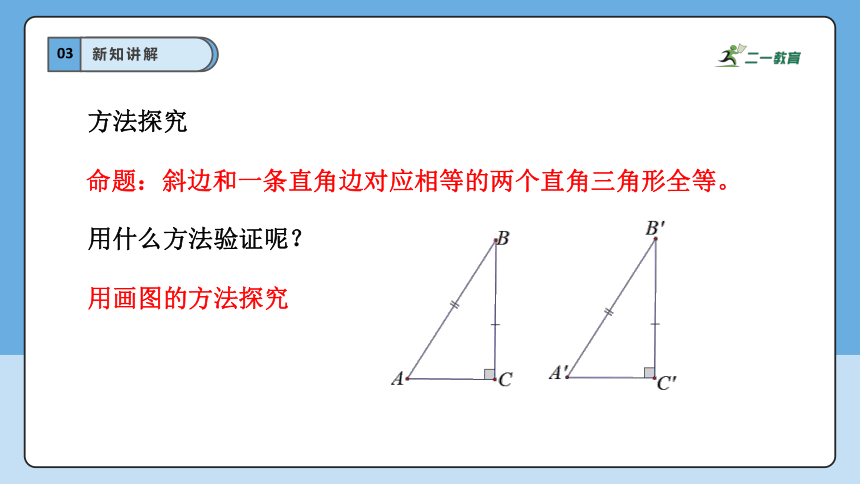
用画图的方法探究
方法探究
用什么方法验证呢?
命题:斜边和一条直角边对应相等的两个直角三角形全等。
03
新知讲解
A
B
C
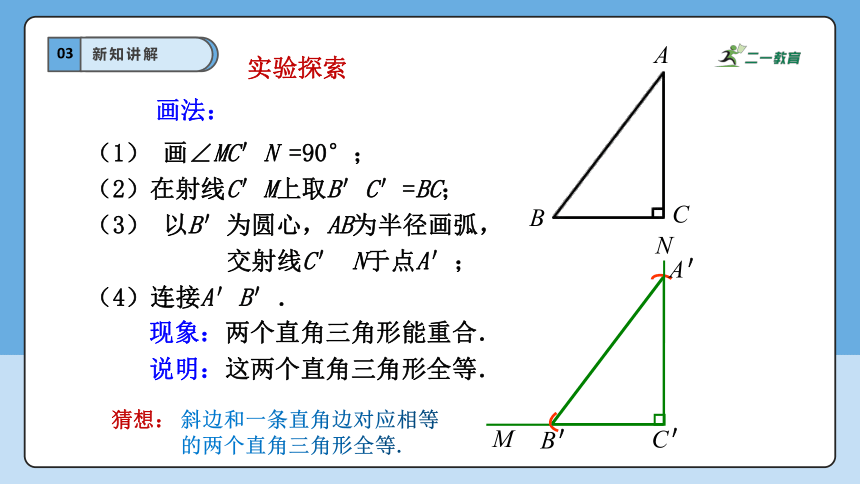
(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B'为圆心,AB为半径画弧,
交射线C' N于点A';
(4)连接A'B'.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A'
N
M
C'
B'
实验探索
猜想:
斜边和一条直角边对应相等的两个直角三角形全等.
03
新知讲解
下面我们给出证明.
已知:如图,在△ACB 和△A'C'B'中,∠C=∠C'=Rt∠,
AB=A'B',AC=A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
A
B
C
A'
B'
C'
03
新知讲解
已知Rt△ABC和Rt△A B C 中,AC’=AC’,AB=A’B’.
证明Rt△ABC≌ Rt△A B C
∵ Rt△ABC和Rt△A B C
∴ BC2=AB2 - AC2
B C 2=A B 2 - A C 2
又∵ AC=AC,AB=AB.
∴BC=B C
在△ABC和△A B C 中
A B=A B
A C=A C BC= B C
证明一
03
新知讲解
A
B
C
A’
B’
C’
∵ ∠ACB=∠A’B’C’=90 °
∴ B,C,B’在同一直线上,
AC ⊥BB’
∵ AB=A'B'
∴ BC=B'C'(等腰三角形三线合一)
∵ AC=A'C'(公共边)
∴ RtΔABC ≌ RtΔA'B'C'(SSS)
证明二
03
新知讲解
提炼概念
简写:“斜边、直角边”或“HL”
A B=A B
A C=A C
直角三角形全等的判定定理:
几何语言:
斜边和一条直角边对应相等的两个直角三角形全等.
( 或BC= B C )
在Rt△ABC与Rt△ A B C 中
B'
C'
A'
A
C
B
03
新知讲解
例
已知:如图,P是∠AOB内一点,PD⊥OA,PE⊥OB,D,E分别是垂足,且PD=PE. 求证:点P在∠AOB的平分线上.
03
新知讲解
证明 如图,作射线OP.
∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°.
又∵OP=OP(公共边),PD=PE(已知),
∴Rt△PDO≌Rt△PEO(HL).
∴∠1=∠2,
即点P在∠AOB的平分线上(角平分线的定义).
03
新知讲解
几何语言:
∵DP⊥OA,PE⊥OB,且DP=EP
∴OP平分∠AOB
角平分线性质定理:
角的内部,到角两边距离相等的点,在这个角的平分线上.
03
新知讲解
归纳概念
1.直角三角形全等的判定定理(HL)
斜边和一条直角边对应相等的两个直角三角形全等.
角的内部,到角两边距离相等的点,在这个角的平分线上。
2.角平分线的性质定理的逆定理:
04
课堂练习
【知识技能类作业】必做题:
1.下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
D
04
课堂练习
【知识技能类作业】必做题:
2.如图,点P是∠CAB内一点,点P到AC,AB的距离分别为PE,PF,且PE=PF.若∠1=20°,则∠CAB等于( )
A.20° B.30° C.40° D.60°
C
04
课堂练习
【知识技能类作业】选做题:
3.如图,AD是△ABC的中线,DE⊥AB于E点,DF⊥AC于F点,且BE=CF。求证:AD平分∠BAC。
证明:在Rt△DEB和Rt△DFC中,
BE=CF,
DB=DC,
∴Rt△DEB≌Rt△DFC(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC(到角的两边距离相等的点在这个角的平分线上)
04
课堂练习
【综合拓展类作业】
4.三条公路两两相交,现在决定在三角形区内建立一个公路维修站,要求到三条公路的距离相等,请问维修站应该建立在何处?请画出图形
L1
L3
04
课堂练习
【综合拓展类作业】
如图所示:
(1)作出△ABC两内角的平分线,其交点为O1;
(2)分别作出△ABC两外角平分线,其交点分别为O2,O3,O4,
故满足条件的修建点有四处,即O1,O2,O3,O4.
21cnjy.com
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1.现要在一块三角形草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在 ( )
A.三角形三条中线的交点
B.三角形三边的垂直平分线的交点
C.三角形三条角平分线的交点
D.三角形三条高所在直线的交点
C
06
作业布置
【知识技能类作业】选做题:
2.如图:在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F
求证:AF平分∠BAC
证明:∵BD⊥AC,CE⊥AB∴∠ADB=∠AEC=90
∵∠BAD=∠CAE,AB=AC
∴△ABD≌△ACE (AAS)
∴AE=AD
∵AF=AF∴△ADF≌△AEF (HL)
∴∠BAF=∠CAF ∴AF平分∠BAC
06
作业布置
【知识技能类作业】选做题:
3.已知,在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.
求证:△ABC是等边三角形.
06
作业布置
【综合拓展类作业】
证明:∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°.
∵D为AC的中点,∴AD=DC.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第二章 特殊三角形
2.8直角三角形全等的判定
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1、探索两个直角三角形全等的条件.
2、握两个直角三角形全等的条件(HL).
3、了解角平分线的性质:角的内部,到角两边距离相等的点,在角平分线上,及其简单应用. 探
02
新知导入
舞台背景的形状是两个直角三角形,工作人员带了量角器和卷尺。如果他想知道两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住,无法测量。
(1) 你能帮他想个办法吗?
生活中的数学
A
C
0
03
新知探究
工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等。于是,他就肯定“两个直角三角形是全等的”。
你认为这个结论对吗?
(2)如果他只带一个卷尺,能完成这个任务吗
斜边和一条直角边对应相等 两个直角三角形全等
A
B
C
D
0
03
新知探究
合作学习
三角形全等的判定
定义:
基本事实:
AAS
证得
复习回顾
能够重合的两个三角形是全等三角形
SSS SAS ASA
03
新知讲解
有两条边和一个角对应相等的两个三角形全等吗?
不全等。理由如下:
如果这个角是直角呢
如图△ABC与△ABD中,
AB=AB,∠B=∠B,AD=AC,
但△ABC与△ABD不全等;
全等
证明你的结论
03
新知讲解
用画图的方法探究
方法探究
用什么方法验证呢?
命题:斜边和一条直角边对应相等的两个直角三角形全等。
03
新知讲解
A
B
C
(1) 画∠MC'N =90°;
(2)在射线C'M上取B'C'=BC;
(3) 以B'为圆心,AB为半径画弧,
交射线C' N于点A';
(4)连接A'B'.
现象:两个直角三角形能重合.
说明:这两个直角三角形全等.
画法:
A'
N
M
C'
B'
实验探索
猜想:
斜边和一条直角边对应相等的两个直角三角形全等.
03
新知讲解
下面我们给出证明.
已知:如图,在△ACB 和△A'C'B'中,∠C=∠C'=Rt∠,
AB=A'B',AC=A'C'.
求证:Rt△ABC≌Rt△A'B'C'.
A
B
C
A'
B'
C'
03
新知讲解
已知Rt△ABC和Rt△A B C 中,AC’=AC’,AB=A’B’.
证明Rt△ABC≌ Rt△A B C
∵ Rt△ABC和Rt△A B C
∴ BC2=AB2 - AC2
B C 2=A B 2 - A C 2
又∵ AC=AC,AB=AB.
∴BC=B C
在△ABC和△A B C 中
A B=A B
A C=A C BC= B C
证明一
03
新知讲解
A
B
C
A’
B’
C’
∵ ∠ACB=∠A’B’C’=90 °
∴ B,C,B’在同一直线上,
AC ⊥BB’
∵ AB=A'B'
∴ BC=B'C'(等腰三角形三线合一)
∵ AC=A'C'(公共边)
∴ RtΔABC ≌ RtΔA'B'C'(SSS)
证明二
03
新知讲解
提炼概念
简写:“斜边、直角边”或“HL”
A B=A B
A C=A C
直角三角形全等的判定定理:
几何语言:
斜边和一条直角边对应相等的两个直角三角形全等.
( 或BC= B C )
在Rt△ABC与Rt△ A B C 中
B'
C'
A'
A
C
B
03
新知讲解
例
已知:如图,P是∠AOB内一点,PD⊥OA,PE⊥OB,D,E分别是垂足,且PD=PE. 求证:点P在∠AOB的平分线上.
03
新知讲解
证明 如图,作射线OP.
∵PD⊥OA,PE⊥OB(已知),
∴∠PDO=∠PEO=90°.
又∵OP=OP(公共边),PD=PE(已知),
∴Rt△PDO≌Rt△PEO(HL).
∴∠1=∠2,
即点P在∠AOB的平分线上(角平分线的定义).
03
新知讲解
几何语言:
∵DP⊥OA,PE⊥OB,且DP=EP
∴OP平分∠AOB
角平分线性质定理:
角的内部,到角两边距离相等的点,在这个角的平分线上.
03
新知讲解
归纳概念
1.直角三角形全等的判定定理(HL)
斜边和一条直角边对应相等的两个直角三角形全等.
角的内部,到角两边距离相等的点,在这个角的平分线上。
2.角平分线的性质定理的逆定理:
04
课堂练习
【知识技能类作业】必做题:
1.下列可使两个直角三角形全等的条件是( )
A.一个锐角对应相等
B.两个锐角对应相等
C.一条边对应相等
D.两条边对应相等
D
04
课堂练习
【知识技能类作业】必做题:
2.如图,点P是∠CAB内一点,点P到AC,AB的距离分别为PE,PF,且PE=PF.若∠1=20°,则∠CAB等于( )
A.20° B.30° C.40° D.60°
C
04
课堂练习
【知识技能类作业】选做题:
3.如图,AD是△ABC的中线,DE⊥AB于E点,DF⊥AC于F点,且BE=CF。求证:AD平分∠BAC。
证明:在Rt△DEB和Rt△DFC中,
BE=CF,
DB=DC,
∴Rt△DEB≌Rt△DFC(HL),
∴DE=DF,
又∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC(到角的两边距离相等的点在这个角的平分线上)
04
课堂练习
【综合拓展类作业】
4.三条公路两两相交,现在决定在三角形区内建立一个公路维修站,要求到三条公路的距离相等,请问维修站应该建立在何处?请画出图形
L1
L3
04
课堂练习
【综合拓展类作业】
如图所示:
(1)作出△ABC两内角的平分线,其交点为O1;
(2)分别作出△ABC两外角平分线,其交点分别为O2,O3,O4,
故满足条件的修建点有四处,即O1,O2,O3,O4.
21cnjy.com
05
课堂小结
06
作业布置
【知识技能类作业】必做题:
1.现要在一块三角形草坪上建一座凉亭供大家休息,要使凉亭到草坪三条边的距离相等,则凉亭的位置应选在 ( )
A.三角形三条中线的交点
B.三角形三边的垂直平分线的交点
C.三角形三条角平分线的交点
D.三角形三条高所在直线的交点
C
06
作业布置
【知识技能类作业】选做题:
2.如图:在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F
求证:AF平分∠BAC
证明:∵BD⊥AC,CE⊥AB∴∠ADB=∠AEC=90
∵∠BAD=∠CAE,AB=AC
∴△ABD≌△ACE (AAS)
∴AE=AD
∵AF=AF∴△ADF≌△AEF (HL)
∴∠BAF=∠CAF ∴AF平分∠BAC
06
作业布置
【知识技能类作业】选做题:
3.已知,在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.
求证:△ABC是等边三角形.
06
作业布置
【综合拓展类作业】
证明:∵DE⊥AB,DF⊥BC,∴∠AED=∠CFD=90°.
∵D为AC的中点,∴AD=DC.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
