3.3.1不等式的基本性质 教学课件(共24张PPT)2025-2026学年浙教版(2024)八年级数学上册
文档属性
| 名称 | 3.3.1不等式的基本性质 教学课件(共24张PPT)2025-2026学年浙教版(2024)八年级数学上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-11 17:29:11 | ||
图片预览






文档简介
3.3.1不等式的基本性质
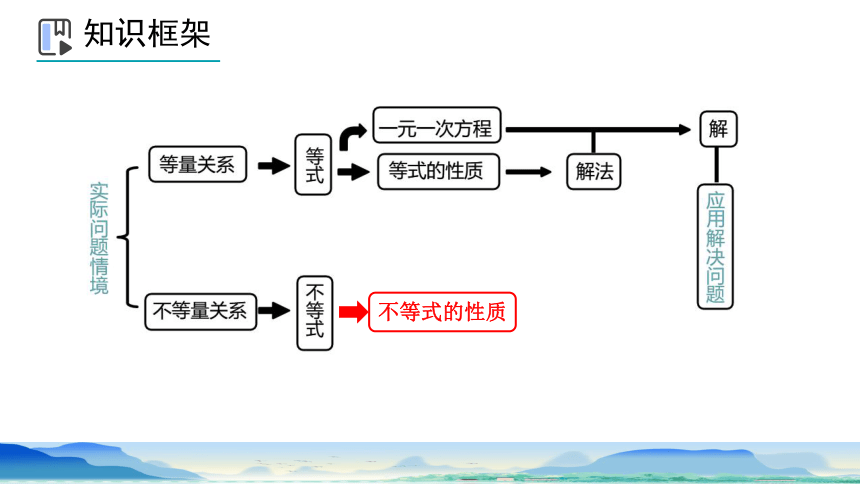
知识框架
不等式的性质
学习目标
1、经历不等式的基本性质的探索过程,掌握不等式的三个性质。
2、能运用不等式的基本性质将简单的不等式转化为“????>????”或“????3、会用不等式的基本性质比较整式的大小。
?
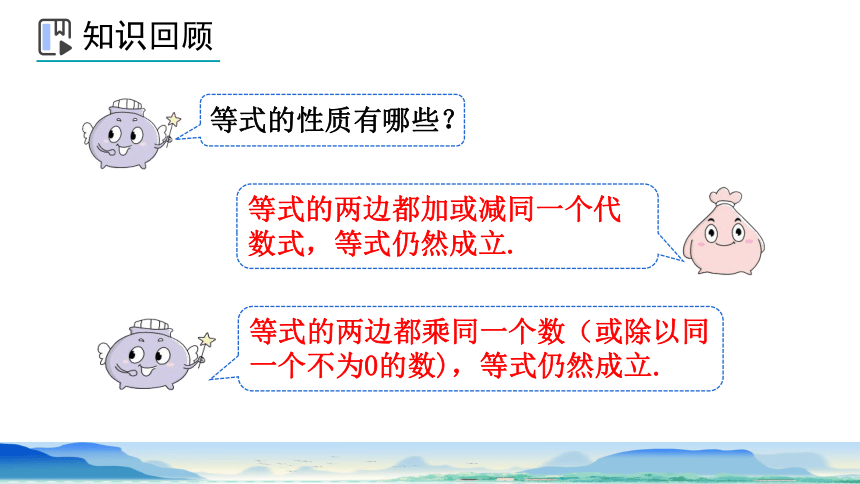
等式的性质有哪些?
等式的两边都加或减同一个代数式,等式仍然成立.
等式的两边都乘同一个数(或除以同一个不为0的数),等式仍然成立.
脑筋急转弯?
有两对父子,为何只有三个人?
70 40
五年后:
70+5 > 40+5
二十年前:
70-20 > 40-20
x年后:
x年前:
70+x > 40+x
70-x > 40-x
>
问:上面四个不等式与原来不等式相比,哪些地方发生了变化?哪些又始终没变?
符号语言:若 a>b,则 a±c > b±c.
不等式的基本性质1
不等式的两边都加(或减)同一个整式,不等号的方向不变。
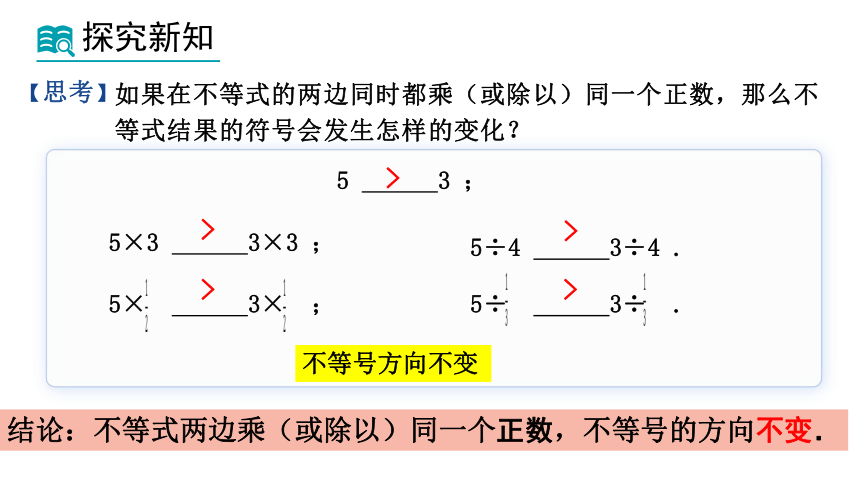
【思考】
如果在不等式的两边同时都乘(或除以)同一个正数,那么不等式结果的符号会发生怎样的变化?
5 3 ;
5×3 3×3 ;
5÷ 3÷ .
>
结论:不等式两边乘(或除以)同一个正数,不等号的方向不变.
12??????????????????????????
?
5× 3× ;
5÷4 3÷4 .
12??????????????????????????
?
13??????????????????????????
?
13??????????????????????????
?
>
>
>
>
不等号方向不变
【思考】
如果在不等式的两边同时都乘(或除以)同一个负数,那么不等式结果的符号会发生怎样的变化?
5 3 ;
5×(-3) 3×(-3) ;
5÷ 3÷ .
>
结论:不等式两边乘(或除以)同一个负数,不等号的方向改变.
5× 3× ;
5÷(-4) 3÷(-4) .
<
<
<
<
不等号方向改变
(?12)
?
(?12)
?
(?12)
?
(?12)
?
不等式的基本性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
符号语言:若a>b,c>0,则ac>bc(或???????? > ????????).
?
不等式的基本性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
符号语言:若a>b,c<0,则ac<bc(或???????? < ????????).
?
两边同乘的数不能是 0,若两边同乘 0,则不等式变为等式 0=0;两边同时除以的数也不能是 0,因为 0 作为除数无意义.
若 ????>????, 用“>”或“<”填空:
?
(1) ?????5 依据:
(2)6+???? 6+???? 依据:
(3) 依据:
(4)?2????? ?2???? 依据:
(5)?2????+1 ?2????+1 依据:
?
>
>
>
<
<
不等式的基本性质1
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
不等式的基本性质1和3
?????5
?
情境延伸
无论绳长l取何值,圆的面积总大于正方形的面积,即
????????????????>????????????????
?
你能利用不等式的基本性质解释这一结论吗?
速记小口诀
加减都用性质1 不等号方向不改变
乘除正数性质2 不等号方向还不变
乘除负数性质3 不等号方向必改变
典例分析
例1 将下列不等式化成“x>a”或“x解:
(1)根据不等式的基本性质1,两边都加5,得
即
(2)根据不等式的基本性质3,两边都除以–2,得
即
1、将下列不等式化成“x>a”或“x典例分析
例2、同桌的甲、乙两名同学,争论着一个问题:
甲同学说:“5a>4a。”乙同学说:“这不可能。”请你判断一下两名同学的观点究竟哪个正确?为什么?
分类讨论
2、比较下列各式的大小,并说出判断依据:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式的性质
不等式的性质1
不等式两边加(或减)同一个整式,不等号的方向 .
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向 .
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向 .
如果a>b,那么a±c>b±c.
如果a>b,c>0,那么ac>bc(或???????? > ????????).
?
不变
不变
改变
如果a>b,c<0,那么ac<bc(或???????? < ????????).
?
1、若 x>y,则ax >ay, 那么一定有( )
A. a>0 B.a≥0 C.a<0 D.a≤0
2.(2024?吉林)不等关系在生活中广泛存在.如图,a、b分别表示两位同学的身高,c表示台阶的高度.图中两人的对话体现的数学原理是( )
A.若a>b,则a+c>b+c
B.若a>b,b>c,则a>c
C.若a>b,c>0,则ac>bc
D.若a>b,c>0,则
A
A
3.(2024?苏州)若a>b﹣1,则下列结论一定正确的是( )
A.a+1<b B.a﹣1<b C.a>b D.a+1>b
4、已知 a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)3a-10 3b -10 .
<
D
<
5、把下列不等式化为 x>a 或 xx < 2;
x < 6.
(1)5>3+x;
(2)2x<x+6.
布置作业
必做题:习题任务单 1-6题.
1
探究性作业:习题任务单 第7题,第8题.
2
A层: 必做题.
B层: 必做题和探究性作业.
在数学天地里,重要的不是我们知道什么,
而是我们怎么知道什么。
---------毕达哥斯拉
知识框架
不等式的性质
学习目标
1、经历不等式的基本性质的探索过程,掌握不等式的三个性质。
2、能运用不等式的基本性质将简单的不等式转化为“????>????”或“????3、会用不等式的基本性质比较整式的大小。
?
等式的性质有哪些?
等式的两边都加或减同一个代数式,等式仍然成立.
等式的两边都乘同一个数(或除以同一个不为0的数),等式仍然成立.
脑筋急转弯?
有两对父子,为何只有三个人?
70 40
五年后:
70+5 > 40+5
二十年前:
70-20 > 40-20
x年后:
x年前:
70+x > 40+x
70-x > 40-x
>
问:上面四个不等式与原来不等式相比,哪些地方发生了变化?哪些又始终没变?
符号语言:若 a>b,则 a±c > b±c.
不等式的基本性质1
不等式的两边都加(或减)同一个整式,不等号的方向不变。
【思考】
如果在不等式的两边同时都乘(或除以)同一个正数,那么不等式结果的符号会发生怎样的变化?
5 3 ;
5×3 3×3 ;
5÷ 3÷ .
>
结论:不等式两边乘(或除以)同一个正数,不等号的方向不变.
12??????????????????????????
?
5× 3× ;
5÷4 3÷4 .
12??????????????????????????
?
13??????????????????????????
?
13??????????????????????????
?
>
>
>
>
不等号方向不变
【思考】
如果在不等式的两边同时都乘(或除以)同一个负数,那么不等式结果的符号会发生怎样的变化?
5 3 ;
5×(-3) 3×(-3) ;
5÷ 3÷ .
>
结论:不等式两边乘(或除以)同一个负数,不等号的方向改变.
5× 3× ;
5÷(-4) 3÷(-4) .
<
<
<
<
不等号方向改变
(?12)
?
(?12)
?
(?12)
?
(?12)
?
不等式的基本性质2
不等式两边乘(或除以)同一个正数,不等号的方向不变.
符号语言:若a>b,c>0,则ac>bc(或???????? > ????????).
?
不等式的基本性质3
不等式两边乘(或除以)同一个负数,不等号的方向改变.
符号语言:若a>b,c<0,则ac<bc(或???????? < ????????).
?
两边同乘的数不能是 0,若两边同乘 0,则不等式变为等式 0=0;两边同时除以的数也不能是 0,因为 0 作为除数无意义.
若 ????>????, 用“>”或“<”填空:
?
(1) ?????5 依据:
(2)6+???? 6+???? 依据:
(3) 依据:
(4)?2????? ?2???? 依据:
(5)?2????+1 ?2????+1 依据:
?
>
>
>
<
<
不等式的基本性质1
不等式的基本性质1
不等式的基本性质2
不等式的基本性质3
不等式的基本性质1和3
?????5
?
情境延伸
无论绳长l取何值,圆的面积总大于正方形的面积,即
????????????????>????????????????
?
你能利用不等式的基本性质解释这一结论吗?
速记小口诀
加减都用性质1 不等号方向不改变
乘除正数性质2 不等号方向还不变
乘除负数性质3 不等号方向必改变
典例分析
例1 将下列不等式化成“x>a”或“x
(1)根据不等式的基本性质1,两边都加5,得
即
(2)根据不等式的基本性质3,两边都除以–2,得
即
1、将下列不等式化成“x>a”或“x
例2、同桌的甲、乙两名同学,争论着一个问题:
甲同学说:“5a>4a。”乙同学说:“这不可能。”请你判断一下两名同学的观点究竟哪个正确?为什么?
分类讨论
2、比较下列各式的大小,并说出判断依据:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式的性质
不等式的性质1
不等式两边加(或减)同一个整式,不等号的方向 .
不等式的性质2
不等式两边乘(或除以)同一个正数,不等号的方向 .
不等式的性质3
不等式两边乘(或除以)同一个负数,不等号的方向 .
如果a>b,那么a±c>b±c.
如果a>b,c>0,那么ac>bc(或???????? > ????????).
?
不变
不变
改变
如果a>b,c<0,那么ac<bc(或???????? < ????????).
?
1、若 x>y,则ax >ay, 那么一定有( )
A. a>0 B.a≥0 C.a<0 D.a≤0
2.(2024?吉林)不等关系在生活中广泛存在.如图,a、b分别表示两位同学的身高,c表示台阶的高度.图中两人的对话体现的数学原理是( )
A.若a>b,则a+c>b+c
B.若a>b,b>c,则a>c
C.若a>b,c>0,则ac>bc
D.若a>b,c>0,则
A
A
3.(2024?苏州)若a>b﹣1,则下列结论一定正确的是( )
A.a+1<b B.a﹣1<b C.a>b D.a+1>b
4、已知 a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)3a-10 3b -10 .
<
D
<
5、把下列不等式化为 x>a 或 xx < 2;
x < 6.
(1)5>3+x;
(2)2x<x+6.
布置作业
必做题:习题任务单 1-6题.
1
探究性作业:习题任务单 第7题,第8题.
2
A层: 必做题.
B层: 必做题和探究性作业.
在数学天地里,重要的不是我们知道什么,
而是我们怎么知道什么。
---------毕达哥斯拉
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
