圆的角度,垂径定理 小结练习(含解析)
文档属性
| 名称 | 圆的角度,垂径定理 小结练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 816.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-11 21:58:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
圆的角度,垂径定理 小结练习
一.选择题(共12小题)
1.三角形的外心具有的性质是( )
A.到三边的距离相等
B.到三个顶点的距离相等
C.外心在三角形外
D.外心在三角形内
2.如图,⊙O的半径OC垂直于弦AB,D是优弧AB上的一点(不与点A、B重合),若∠AOC=50°,则∠CDB等于( )
A.25° B.30° C.40° D.50°
3.在直径为26cm的圆柱形容器装进一些水后,其横截面如图所示.已知水面的宽度AB=24cm,则水的最大深度为( )
A.5cm B.7cm C.8cm D.10cm
4.杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为3.2m,拱高(桥拱圆弧的中点到弦的距离)约为2m,则此桥拱的半径是( )
A.1.62m B.1.64m C.1.14m D.3.56m
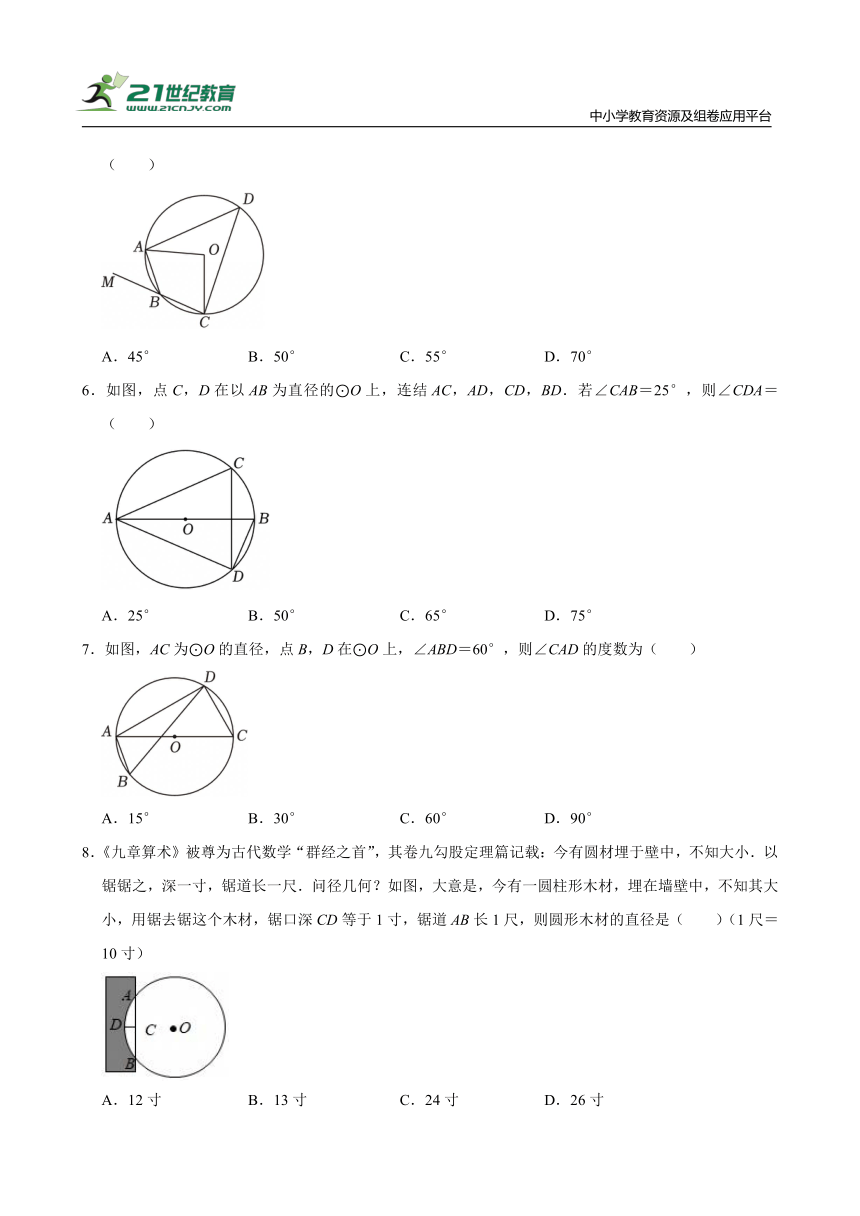
5.如图,四边形ABCD内接于⊙O,点M为边CB延长线上一点.若∠AOC=110°,则∠ABM的度数是( )
A.45° B.50° C.55° D.70°
6.如图,点C,D在以AB为直径的⊙O上,连结AC,AD,CD,BD.若∠CAB=25°,则∠CDA=( )
A.25° B.50° C.65° D.75°
7.如图,AC为⊙O的直径,点B,D在⊙O上,∠ABD=60°,则∠CAD的度数为( )
A.15° B.30° C.60° D.90°
8.《九章算术》被尊为古代数学“群经之首”,其卷九勾股定理篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这个木材,锯口深CD等于1寸,锯道AB长1尺,则圆形木材的直径是( )(1尺=10寸)
A.12寸 B.13寸 C.24寸 D.26寸
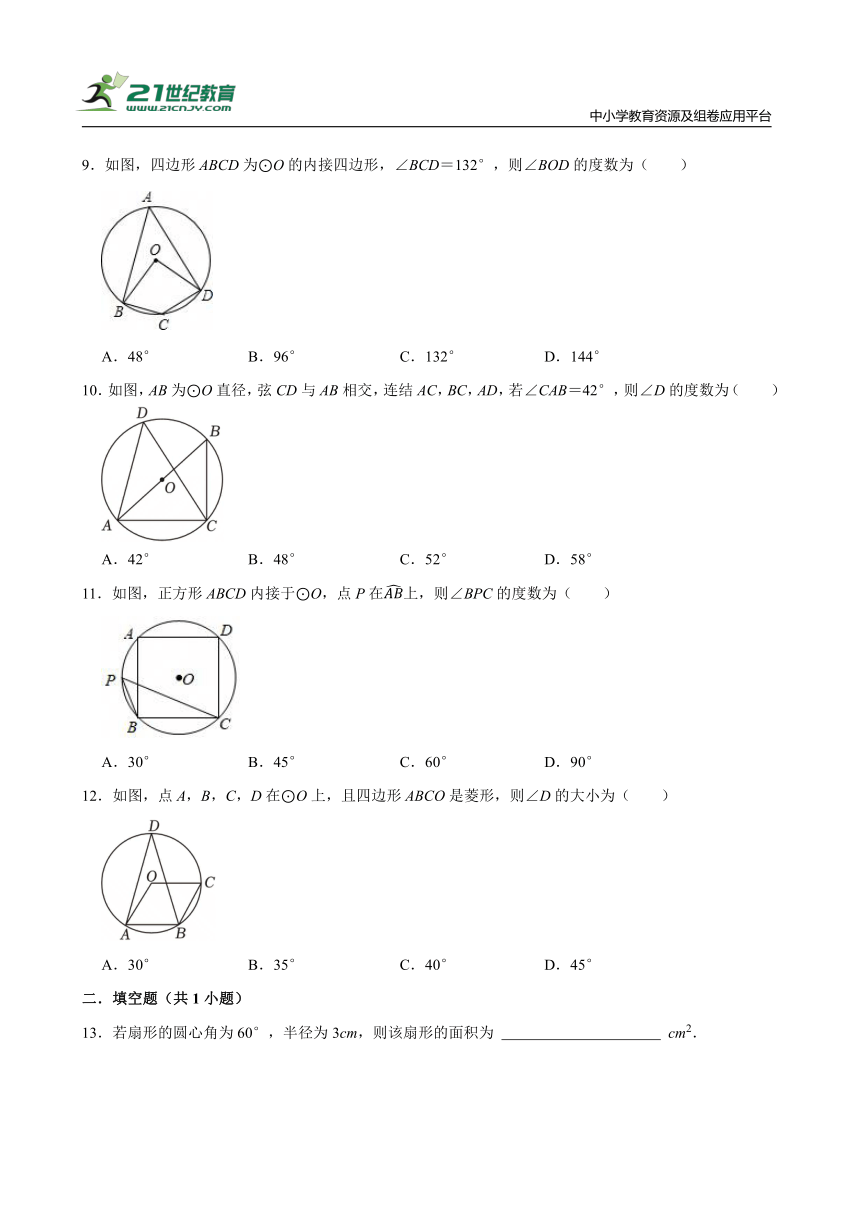
9.如图,四边形ABCD为⊙O的内接四边形,∠BCD=132°,则∠BOD的度数为( )
A.48° B.96° C.132° D.144°
10.如图,AB为⊙O直径,弦CD与AB相交,连结AC,BC,AD,若∠CAB=42°,则∠D的度数为( )
A.42° B.48° C.52° D.58°
11.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
12.如图,点A,B,C,D在⊙O上,且四边形ABCO是菱形,则∠D的大小为( )
A.30° B.35° C.40° D.45°
二.填空题(共1小题)
13.若扇形的圆心角为60°,半径为3cm,则该扇形的面积为 cm2.
圆的角度,垂径定理 小结练习
一.选择题(共12小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B A C B C C B D B B B
题号 12
答案 A
一.选择题(共12小题)
1.三角形的外心具有的性质是( )
A.到三边的距离相等
B.到三个顶点的距离相等
C.外心在三角形外
D.外心在三角形内
【思路点拔】根据三角形外心的定义进行解答即可.
【解答】解:A、∵三角形的外心是三角形三条边垂直平分线的交点,∴到三边的距离相等不一定相等,故本选项错误;
B、∵三角形的外心是三角形三条边垂直平分线的交点,∴到三个顶点的距离相等相等,故本选项正确;
C、∵锐角三角形的外心在三角形的内部,∴外心不一定在三角形外,故本选项错误;
D、∵顿角三角形的外心在三角形的外部,∴外心不一定在三角形内,故本选项错误.
故选:B.
【点评】本题考查的是三角形的外接圆与外心,熟知三角形外接圆的圆心是三角形三条边垂直平分线的交点是解答此题的关键.
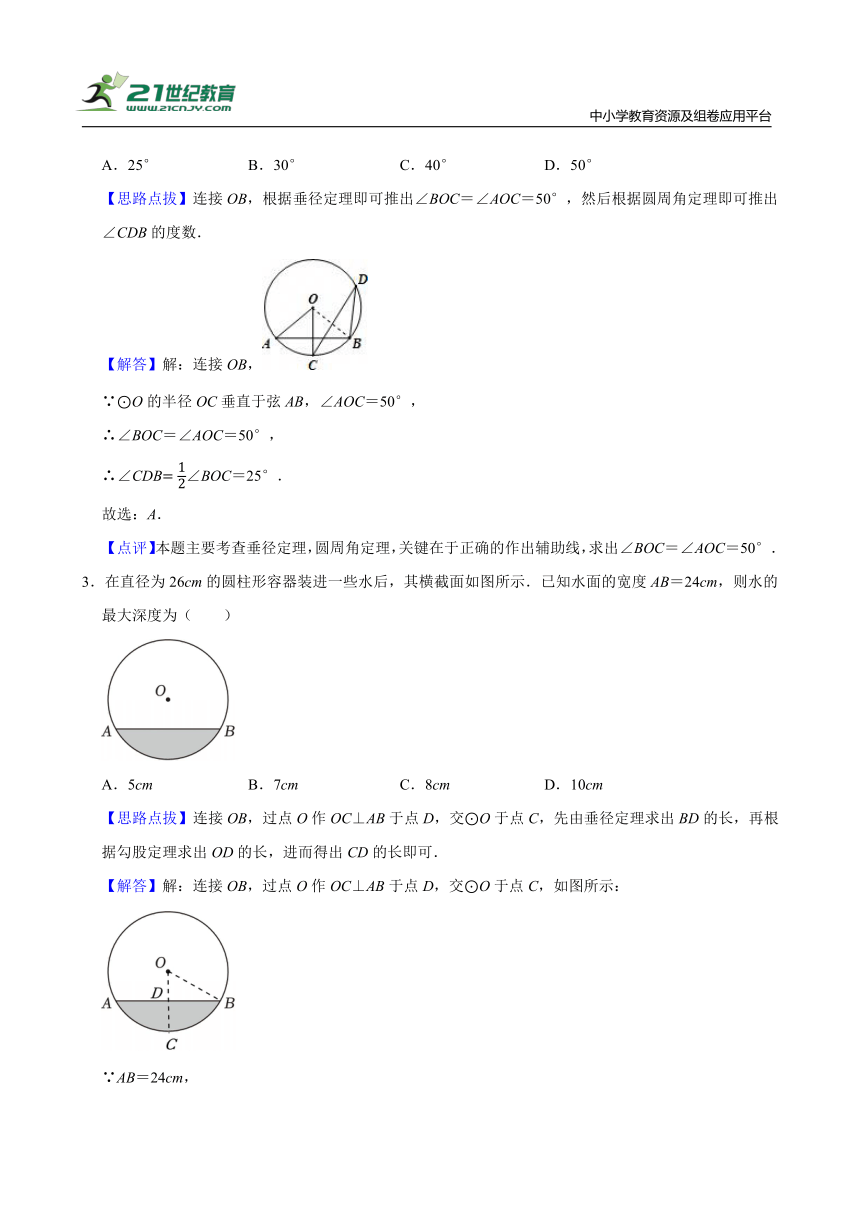
2.如图,⊙O的半径OC垂直于弦AB,D是优弧AB上的一点(不与点A、B重合),若∠AOC=50°,则∠CDB等于( )
A.25° B.30° C.40° D.50°
【思路点拔】连接OB,根据垂径定理即可推出∠BOC=∠AOC=50°,然后根据圆周角定理即可推出∠CDB的度数.
【解答】解:连接OB,
∵⊙O的半径OC垂直于弦AB,∠AOC=50°,
∴∠BOC=∠AOC=50°,
∴∠CDB∠BOC=25°.
故选:A.
【点评】本题主要考查垂径定理,圆周角定理,关键在于正确的作出辅助线,求出∠BOC=∠AOC=50°.
3.在直径为26cm的圆柱形容器装进一些水后,其横截面如图所示.已知水面的宽度AB=24cm,则水的最大深度为( )
A.5cm B.7cm C.8cm D.10cm
【思路点拔】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而得出CD的长即可.
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BDAB=12(cm),
∵⊙O的直径为26cm,
∴OB=OC=13cm,
在Rt△OBD中,OD5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:C.
【点评】本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键.
4.杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为3.2m,拱高(桥拱圆弧的中点到弦的距离)约为2m,则此桥拱的半径是( )
A.1.62m B.1.64m C.1.14m D.3.56m
【思路点拔】设圆心为O,作OD⊥AB于点D,DO的延长线交圆弧为点C,设半径为Rm,根据垂径定理得AD=BD=1.6m,OD=(2﹣R)m,由勾股定理得:R2=1.62+(2﹣R)2,即可求出答案.
【解答】解:如图,设圆心为O,作OD⊥AB于点D,DO的延长线交圆弧为点C,则C为优弧AB的中点,设半径为R m,
∴AD=BDAB=1.6m,CD=2m,
∴OD=(2﹣R)m,
由勾股定理得:OA2=OD2+AD2,
∴R2=1.62+(2﹣R)2,
解得:R=1.64,
故选:B.
【点评】该题主要考查了垂径定理、勾股定理及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.
5.如图,四边形ABCD内接于⊙O,点M为边CB延长线上一点.若∠AOC=110°,则∠ABM的度数是( )
A.45° B.50° C.55° D.70°
【思路点拔】由圆周角定理得到∠D∠AOC=55°,由圆内接四边形的性质和邻补角的性质推出∠ABM=∠D=55°.
【解答】解:∵∠AOC=110°,
∴∠D∠AOC=55°,
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∵∠ABM+∠ABC=180°,
∴∠ABM=∠D=55°.
故选:C.
【点评】本题考查圆周角定理,圆内接四边形的性质,关键是由圆周角定理得到∠D∠AOC,由圆内接四边形的性质推出∠ABM=∠D=55°.
6.如图,点C,D在以AB为直径的⊙O上,连结AC,AD,CD,BD.若∠CAB=25°,则∠CDA=( )
A.25° B.50° C.65° D.75°
【思路点拔】先根据AB为⊙O的直径得出∠ADB=90°,再由∠CAB=25°得出∠BDC=25°,进而可得出结论.
【解答】解:∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠CAB=25°,
∴∠BDC=∠CAB=25°,
∴∠CDA=∠ADB﹣∠BDC=90°﹣25°=65°.
故选:C.
【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等是解题的关键.
7.如图,AC为⊙O的直径,点B,D在⊙O上,∠ABD=60°,则∠CAD的度数为( )
A.15° B.30° C.60° D.90°
【思路点拔】由圆周角定理可得:∠ADC=90°,∠ACD=∠ABD=60°,则答案可解.
【解答】解:∵AC为⊙O的直径,
∴∠ADC=90°,
∵∠ACD=∠ABD,∠ABD=60°,
∴∠ACD=60°,
∴∠CAD=90°﹣∠ACD=90°﹣60°=30°,
故选:B.
【点评】本题主要考查了圆周角,掌握同弧所对的圆周角相等,直径所对的圆周角为直角是解题的关键.
8.《九章算术》被尊为古代数学“群经之首”,其卷九勾股定理篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这个木材,锯口深CD等于1寸,锯道AB长1尺,则圆形木材的直径是( )(1尺=10寸)
A.12寸 B.13寸 C.24寸 D.26寸
【思路点拔】连接OA、OC,由垂径定理得AC=BCAB=5寸,连接OA,设圆的半径为x寸,再在Rt△OAC中,由勾股定理列出方程,解方程可得半径,进而直径可求.
【解答】解:连接OA、OC,如图:
由题意得:C为AB的中点,
则O、C、D三点共线,OC⊥AB,
∴AC=BCAB=5(寸),
设圆的半径为x寸,则OC=(x﹣1)寸.
在Rt△OAC中,由勾股定理得:52+(x﹣1)2=x2,
解得:x=13.
∴圆材直径为2×13=26(寸).
故选:D.
【点评】本题主要考查了垂径定理的应用,勾股定理的应用,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
9.如图,四边形ABCD为⊙O的内接四边形,∠BCD=132°,则∠BOD的度数为( )
A.48° B.96° C.132° D.144°
【思路点拔】根据圆内接四边形的性质得出∠A+∠BCD=180°,求出∠A=48°,根据圆周角定理得出∠BOD=2∠A,再求出答案即可.
【解答】解:∵四边形ABCD为⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠BCD=132°,
∴∠A=48°,
∵对的圆周角是∠A,对的圆心角是∠BOD,
∴∠BOD=2∠A=96°,
故选:B.
【点评】本题考查了圆周角定理,和圆内接四边形的性质等知识点,能综合运用知识点进行推理和计算是解此题的关键,注意:圆内接四边形的对角互补,②一条弧所对的圆周角等于圆心角的一半.
10.如图,AB为⊙O直径,弦CD与AB相交,连结AC,BC,AD,若∠CAB=42°,则∠D的度数为( )
A.42° B.48° C.52° D.58°
【思路点拔】由AB为⊙O直径,则∠ACB=90°,由直角三角形的性质得∠B=48°,最后由圆周角定理即可求解.
【解答】解:∵AB为⊙O直径,
∴∠ACB=90°,
由条件可知∠B=48°,
∴∠D=∠B=48°,
故选:B.
【点评】此题考查了圆周角定理,直角三角形的性质,熟练掌握圆周角的有关性质是解题的关键.
11.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
【思路点拔】根据正方形的性质得到BC弧所对的圆心角为90°,则∠BOC=90°,然后根据圆周角定理求解.
【解答】解:连接OB、OC,如图,
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC∠BOC=45°.
故选:B.
【点评】本题考查了圆周角定理和正方形的性质,确定BC弧所对的圆心角为90°,是本题解题的关键.
12.如图,点A,B,C,D在⊙O上,且四边形ABCO是菱形,则∠D的大小为( )
A.30° B.35° C.40° D.45°
【思路点拔】连接CD,设∠ADB=x,先根据菱形的性质可得AB=BC,∠O=∠ABC,再求出∠CDB=∠ADB=x,然后根据圆周角定理可得∠ABC=∠O=2∠ADC=4x,最后根据圆内接四边形的性质可得∠ABC+∠ADC=180°,由此即可得∠ADB=30°.
【解答】解:如图,连接CD,
设∠ADB=x,
由条件可知AB=BC,∠O=∠ABC,
∴,
∴∠CDB=∠ADB=x,
∴∠ADC=∠CDB+∠ADB=2x,
由圆周角定理得:∠O=2∠ADC=4x,
∴∠ABC=4x,
由条件可知∠ABC+∠ADC=180°,
∴4x+2x=180°,
解得x=30°,
∴∠ADB=30°,
故选:A.
【点评】本题考查了菱形的性质、圆周角定理、圆内接四边形等知识,熟练掌握圆周角定理和圆内接四边形的性质是解题关键.
二.填空题(共1小题)
13.若扇形的圆心角为60°,半径为3cm,则该扇形的面积为 π cm2.
【思路点拔】直接根据扇形的面积公式计算即可.
【解答】解:该扇形的面积为 π(cm2).
故答案为:π.
【点评】本题考查扇形的面积,解题的关键是记住扇形的面积公式,属于中考常考题型.
圆的角度,垂径定理 小结练习
一.选择题(共12小题)
1.三角形的外心具有的性质是( )
A.到三边的距离相等
B.到三个顶点的距离相等
C.外心在三角形外
D.外心在三角形内
2.如图,⊙O的半径OC垂直于弦AB,D是优弧AB上的一点(不与点A、B重合),若∠AOC=50°,则∠CDB等于( )
A.25° B.30° C.40° D.50°
3.在直径为26cm的圆柱形容器装进一些水后,其横截面如图所示.已知水面的宽度AB=24cm,则水的最大深度为( )
A.5cm B.7cm C.8cm D.10cm
4.杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为3.2m,拱高(桥拱圆弧的中点到弦的距离)约为2m,则此桥拱的半径是( )
A.1.62m B.1.64m C.1.14m D.3.56m
5.如图,四边形ABCD内接于⊙O,点M为边CB延长线上一点.若∠AOC=110°,则∠ABM的度数是( )
A.45° B.50° C.55° D.70°
6.如图,点C,D在以AB为直径的⊙O上,连结AC,AD,CD,BD.若∠CAB=25°,则∠CDA=( )
A.25° B.50° C.65° D.75°
7.如图,AC为⊙O的直径,点B,D在⊙O上,∠ABD=60°,则∠CAD的度数为( )
A.15° B.30° C.60° D.90°
8.《九章算术》被尊为古代数学“群经之首”,其卷九勾股定理篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这个木材,锯口深CD等于1寸,锯道AB长1尺,则圆形木材的直径是( )(1尺=10寸)
A.12寸 B.13寸 C.24寸 D.26寸
9.如图,四边形ABCD为⊙O的内接四边形,∠BCD=132°,则∠BOD的度数为( )
A.48° B.96° C.132° D.144°
10.如图,AB为⊙O直径,弦CD与AB相交,连结AC,BC,AD,若∠CAB=42°,则∠D的度数为( )
A.42° B.48° C.52° D.58°
11.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
12.如图,点A,B,C,D在⊙O上,且四边形ABCO是菱形,则∠D的大小为( )
A.30° B.35° C.40° D.45°
二.填空题(共1小题)
13.若扇形的圆心角为60°,半径为3cm,则该扇形的面积为 cm2.
圆的角度,垂径定理 小结练习
一.选择题(共12小题)
题号 1 2 3 4 5 6 7 8 9 10 11
答案 B A C B C C B D B B B
题号 12
答案 A
一.选择题(共12小题)
1.三角形的外心具有的性质是( )
A.到三边的距离相等
B.到三个顶点的距离相等
C.外心在三角形外
D.外心在三角形内
【思路点拔】根据三角形外心的定义进行解答即可.
【解答】解:A、∵三角形的外心是三角形三条边垂直平分线的交点,∴到三边的距离相等不一定相等,故本选项错误;
B、∵三角形的外心是三角形三条边垂直平分线的交点,∴到三个顶点的距离相等相等,故本选项正确;
C、∵锐角三角形的外心在三角形的内部,∴外心不一定在三角形外,故本选项错误;
D、∵顿角三角形的外心在三角形的外部,∴外心不一定在三角形内,故本选项错误.
故选:B.
【点评】本题考查的是三角形的外接圆与外心,熟知三角形外接圆的圆心是三角形三条边垂直平分线的交点是解答此题的关键.
2.如图,⊙O的半径OC垂直于弦AB,D是优弧AB上的一点(不与点A、B重合),若∠AOC=50°,则∠CDB等于( )
A.25° B.30° C.40° D.50°
【思路点拔】连接OB,根据垂径定理即可推出∠BOC=∠AOC=50°,然后根据圆周角定理即可推出∠CDB的度数.
【解答】解:连接OB,
∵⊙O的半径OC垂直于弦AB,∠AOC=50°,
∴∠BOC=∠AOC=50°,
∴∠CDB∠BOC=25°.
故选:A.
【点评】本题主要考查垂径定理,圆周角定理,关键在于正确的作出辅助线,求出∠BOC=∠AOC=50°.
3.在直径为26cm的圆柱形容器装进一些水后,其横截面如图所示.已知水面的宽度AB=24cm,则水的最大深度为( )
A.5cm B.7cm C.8cm D.10cm
【思路点拔】连接OB,过点O作OC⊥AB于点D,交⊙O于点C,先由垂径定理求出BD的长,再根据勾股定理求出OD的长,进而得出CD的长即可.
【解答】解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=24cm,
∴BDAB=12(cm),
∵⊙O的直径为26cm,
∴OB=OC=13cm,
在Rt△OBD中,OD5(cm),
∴CD=OC﹣OD=13﹣5=8(cm),
即水的最大深度为8cm,
故选:C.
【点评】本题考查了垂径定理、勾股定理等知识;根据题意作出辅助线,构造出直角三角形是解答此题的关键.
4.杭州亚运会开幕式出现一座古今交汇拱底桥,桥面呈拱形.该桥的中间拱洞可以看成一种特殊的圆拱桥,此圆拱桥的跨径(桥拱圆弧所对的弦的长)约为3.2m,拱高(桥拱圆弧的中点到弦的距离)约为2m,则此桥拱的半径是( )
A.1.62m B.1.64m C.1.14m D.3.56m
【思路点拔】设圆心为O,作OD⊥AB于点D,DO的延长线交圆弧为点C,设半径为Rm,根据垂径定理得AD=BD=1.6m,OD=(2﹣R)m,由勾股定理得:R2=1.62+(2﹣R)2,即可求出答案.
【解答】解:如图,设圆心为O,作OD⊥AB于点D,DO的延长线交圆弧为点C,则C为优弧AB的中点,设半径为R m,
∴AD=BDAB=1.6m,CD=2m,
∴OD=(2﹣R)m,
由勾股定理得:OA2=OD2+AD2,
∴R2=1.62+(2﹣R)2,
解得:R=1.64,
故选:B.
【点评】该题主要考查了垂径定理、勾股定理及其应用问题;解题的关键是灵活运用有关定理来分析、判断、推理或解答.
5.如图,四边形ABCD内接于⊙O,点M为边CB延长线上一点.若∠AOC=110°,则∠ABM的度数是( )
A.45° B.50° C.55° D.70°
【思路点拔】由圆周角定理得到∠D∠AOC=55°,由圆内接四边形的性质和邻补角的性质推出∠ABM=∠D=55°.
【解答】解:∵∠AOC=110°,
∴∠D∠AOC=55°,
∵四边形ABCD是圆内接四边形,
∴∠D+∠ABC=180°,
∵∠ABM+∠ABC=180°,
∴∠ABM=∠D=55°.
故选:C.
【点评】本题考查圆周角定理,圆内接四边形的性质,关键是由圆周角定理得到∠D∠AOC,由圆内接四边形的性质推出∠ABM=∠D=55°.
6.如图,点C,D在以AB为直径的⊙O上,连结AC,AD,CD,BD.若∠CAB=25°,则∠CDA=( )
A.25° B.50° C.65° D.75°
【思路点拔】先根据AB为⊙O的直径得出∠ADB=90°,再由∠CAB=25°得出∠BDC=25°,进而可得出结论.
【解答】解:∵AB为⊙O的直径,
∴∠ADB=90°,
∵∠CAB=25°,
∴∠BDC=∠CAB=25°,
∴∠CDA=∠ADB﹣∠BDC=90°﹣25°=65°.
故选:C.
【点评】本题考查的是圆周角定理,熟知在同圆或等圆中,同弧或等弧所对的圆周角相等是解题的关键.
7.如图,AC为⊙O的直径,点B,D在⊙O上,∠ABD=60°,则∠CAD的度数为( )
A.15° B.30° C.60° D.90°
【思路点拔】由圆周角定理可得:∠ADC=90°,∠ACD=∠ABD=60°,则答案可解.
【解答】解:∵AC为⊙O的直径,
∴∠ADC=90°,
∵∠ACD=∠ABD,∠ABD=60°,
∴∠ACD=60°,
∴∠CAD=90°﹣∠ACD=90°﹣60°=30°,
故选:B.
【点评】本题主要考查了圆周角,掌握同弧所对的圆周角相等,直径所对的圆周角为直角是解题的关键.
8.《九章算术》被尊为古代数学“群经之首”,其卷九勾股定理篇记载:今有圆材埋于壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?如图,大意是,今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这个木材,锯口深CD等于1寸,锯道AB长1尺,则圆形木材的直径是( )(1尺=10寸)
A.12寸 B.13寸 C.24寸 D.26寸
【思路点拔】连接OA、OC,由垂径定理得AC=BCAB=5寸,连接OA,设圆的半径为x寸,再在Rt△OAC中,由勾股定理列出方程,解方程可得半径,进而直径可求.
【解答】解:连接OA、OC,如图:
由题意得:C为AB的中点,
则O、C、D三点共线,OC⊥AB,
∴AC=BCAB=5(寸),
设圆的半径为x寸,则OC=(x﹣1)寸.
在Rt△OAC中,由勾股定理得:52+(x﹣1)2=x2,
解得:x=13.
∴圆材直径为2×13=26(寸).
故选:D.
【点评】本题主要考查了垂径定理的应用,勾股定理的应用,熟练掌握垂径定理,由勾股定理得出方程是解题的关键.
9.如图,四边形ABCD为⊙O的内接四边形,∠BCD=132°,则∠BOD的度数为( )
A.48° B.96° C.132° D.144°
【思路点拔】根据圆内接四边形的性质得出∠A+∠BCD=180°,求出∠A=48°,根据圆周角定理得出∠BOD=2∠A,再求出答案即可.
【解答】解:∵四边形ABCD为⊙O的内接四边形,
∴∠A+∠BCD=180°,
∵∠BCD=132°,
∴∠A=48°,
∵对的圆周角是∠A,对的圆心角是∠BOD,
∴∠BOD=2∠A=96°,
故选:B.
【点评】本题考查了圆周角定理,和圆内接四边形的性质等知识点,能综合运用知识点进行推理和计算是解此题的关键,注意:圆内接四边形的对角互补,②一条弧所对的圆周角等于圆心角的一半.
10.如图,AB为⊙O直径,弦CD与AB相交,连结AC,BC,AD,若∠CAB=42°,则∠D的度数为( )
A.42° B.48° C.52° D.58°
【思路点拔】由AB为⊙O直径,则∠ACB=90°,由直角三角形的性质得∠B=48°,最后由圆周角定理即可求解.
【解答】解:∵AB为⊙O直径,
∴∠ACB=90°,
由条件可知∠B=48°,
∴∠D=∠B=48°,
故选:B.
【点评】此题考查了圆周角定理,直角三角形的性质,熟练掌握圆周角的有关性质是解题的关键.
11.如图,正方形ABCD内接于⊙O,点P在上,则∠BPC的度数为( )
A.30° B.45° C.60° D.90°
【思路点拔】根据正方形的性质得到BC弧所对的圆心角为90°,则∠BOC=90°,然后根据圆周角定理求解.
【解答】解:连接OB、OC,如图,
∵正方形ABCD内接于⊙O,
∴所对的圆心角为90°,
∴∠BOC=90°,
∴∠BPC∠BOC=45°.
故选:B.
【点评】本题考查了圆周角定理和正方形的性质,确定BC弧所对的圆心角为90°,是本题解题的关键.
12.如图,点A,B,C,D在⊙O上,且四边形ABCO是菱形,则∠D的大小为( )
A.30° B.35° C.40° D.45°
【思路点拔】连接CD,设∠ADB=x,先根据菱形的性质可得AB=BC,∠O=∠ABC,再求出∠CDB=∠ADB=x,然后根据圆周角定理可得∠ABC=∠O=2∠ADC=4x,最后根据圆内接四边形的性质可得∠ABC+∠ADC=180°,由此即可得∠ADB=30°.
【解答】解:如图,连接CD,
设∠ADB=x,
由条件可知AB=BC,∠O=∠ABC,
∴,
∴∠CDB=∠ADB=x,
∴∠ADC=∠CDB+∠ADB=2x,
由圆周角定理得:∠O=2∠ADC=4x,
∴∠ABC=4x,
由条件可知∠ABC+∠ADC=180°,
∴4x+2x=180°,
解得x=30°,
∴∠ADB=30°,
故选:A.
【点评】本题考查了菱形的性质、圆周角定理、圆内接四边形等知识,熟练掌握圆周角定理和圆内接四边形的性质是解题关键.
二.填空题(共1小题)
13.若扇形的圆心角为60°,半径为3cm,则该扇形的面积为 π cm2.
【思路点拔】直接根据扇形的面积公式计算即可.
【解答】解:该扇形的面积为 π(cm2).
故答案为:π.
【点评】本题考查扇形的面积,解题的关键是记住扇形的面积公式,属于中考常考题型.
同课章节目录
