1.3.2 证明 教案

中小学教育资源及组卷应用平台
分课时教学设计
第6课时《1.3.2 证明 》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 证明三角形内角和定理，掌握它的推论，并能运用这些定理解决简单的问题；经历探索与证明的过程，进一步发展推理论证能力；再次“尝试”证明，让学生充分发挥自已的知识积淀，从而对证明的格式有更深的理解.
学习者分析 通过多种思考方法的交流，促进学生发散思考，并在交流中，发展学生的合乎逻辑的思维、有条理的表达能力.
教学目标 掌握三角形的内角和定理及推论，并能进行简单的运用； 2.了解证明命题的格式和一般步骤．
教学重点 继续学会证明的方法和表述.
教学难点 例4需添辅助线，证明思路不易形成.
学习活动设计
教师活动学生活动环节一：引入新课 要判定一个命题是真命题，往往需要从命题的条件出发，根据已知的定义、基本事实、定理，一步一步推出结论成立，这样的推理过程叫做证明. 学生活动1： 学生在教师的引导下，能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明：激发学生兴趣,引入新课主题，激发学生的兴趣，理解学生思考，再次“尝试”证明，让学生充分发挥自已的知识积淀，从而对证明的格式有更深的理解． 环节二：新知探究教师活动2： 从基本事实“两直线平行，同位角相等”出发，如何证明“两直线平行，内错角相等”？ 1.画出图形，并根据图形写出已知、求证； 2.说出你的证题思路； 3.完成证明，并与同学交流. 学生活动2： 学生自学、互动。在具体计算时，可以通过小组合作交流，放手让学生去思考、讨论，猜想、发现结论． 学生自主解答，教师适时的进行提示 学生思考 活动意图说明：从旧知识出发，呼应引课问题，学生通过自己解决问题，让学生在小组内共同合作．通过大家思维的互补从而得出最佳的结果.这里也可让学生板演，让学生自主地写出完整的讲明过程，教师要引导学生，也可让学生自己分析． 环节三：典例精析 例3 证明命题“三角形三个内角的和等于180°”是真命题. 已知：∠BAC，∠B，∠C是△ABC的三个内角. 求证：∠BAC+∠B+∠C=180°. 证明：过A 作 AE // BC 则∠C＝∠2，∠B＝∠1 （两直线平行，内错角相等） ∴∠BAC+∠B+∠C ＝∠BAC+∠1+∠2 ＝∠DAE＝180 （平角的定义） 在解决几何问题时,有时需要添加辅助线,添辅助线的过程要写入证明中, 辅助线通常画成虚线。 你还有其他证明方法吗？ 证法2：作BC的延长线CD，过点C作射线CE//AB，则 ∠1＝∠Ａ（两直线平行，内错角相等） ∠2＝∠Ｂ（两直线平行，同位角相等） ∵∠1+∠2+∠ACB＝180° ∴∠Ａ+∠Ｂ+∠ACB＝180° 证法3:证明：在BC上任取一点D，过D作DE//AB，作DF//AC。 ∴∠1=∠B，∠2=∠C，∠DEC=∠A，
∵DE∥AB，∴∠3=∠DEC，
∴∠3=∠A，
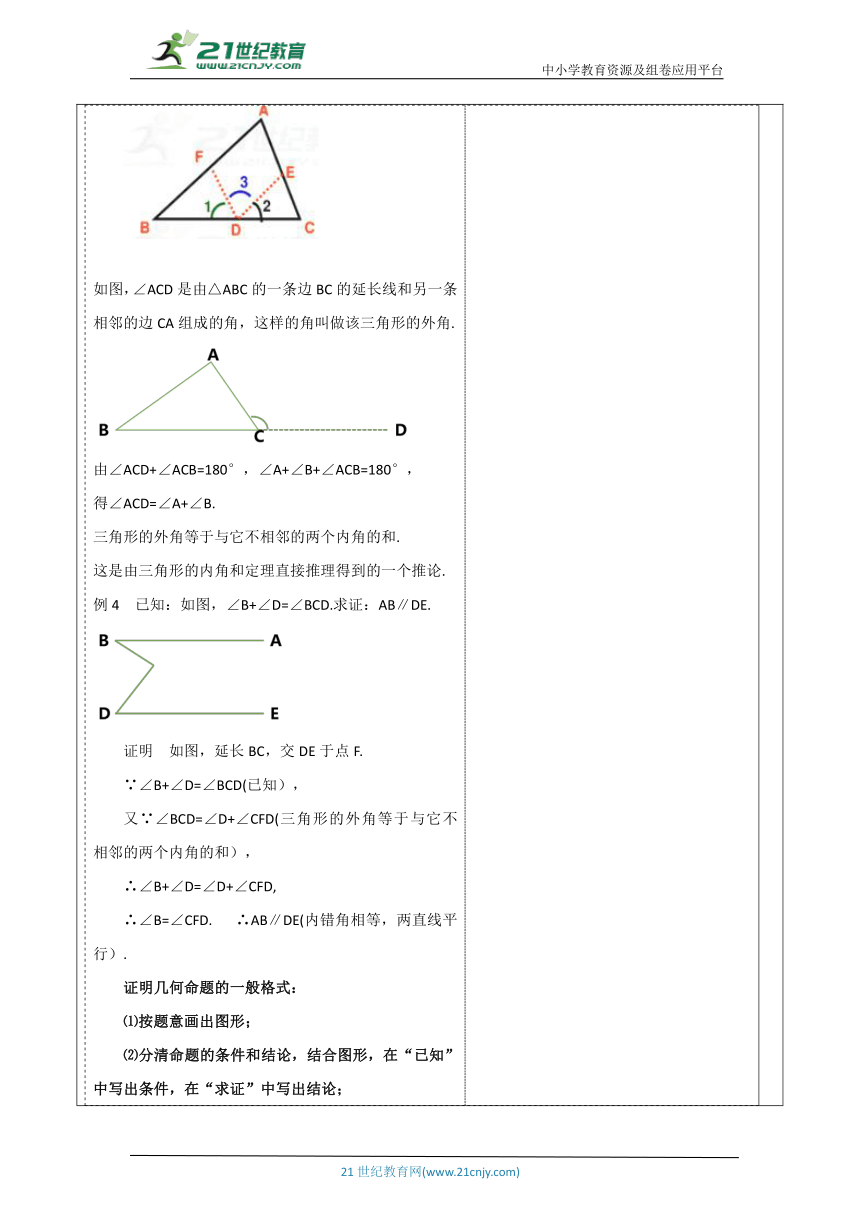
∵∠1+∠2+∠3=180° ∴∠Ａ+∠Ｂ+∠Ｃ＝180° 如图，∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边CA组成的角，这样的角叫做该三角形的外角. 由∠ACD+∠ACB=180°，∠A+∠B+∠ACB=180°， 得∠ACD=∠A+∠B. 三角形的外角等于与它不相邻的两个内角的和. 这是由三角形的内角和定理直接推理得到的一个推论. 例4 已知：如图，∠B+∠D=∠BCD.求证：AB∥DE. 证明 如图，延长BC，交DE于点F. ∵∠B+∠D=∠BCD(已知）， 又∵∠BCD=∠D+∠CFD(三角形的外角等于与它不相邻的两个内角的和）， ∴∠B+∠D=∠D+∠CFD, ∴∠B=∠CFD. ∴AB∥DE(内错角相等，两直线平行）. 证明几何命题的一般格式： ⑴按题意画出图形； ⑵分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论； ⑶在“证明”中写出推理过程 学生活动3： 参与教师分析和讲例题． 活动意图说明：熟练掌握.巩固学的知识，学生通过自己解决问题，充分发挥学习的主动性，感受数学的严谨，初步养成言之有理、落笔有据的推理习惯，感受数学的魅力．
板书设计
课堂练习 【知识技能类作业】 必做题： 1．如图，下列关于△ABC的外角的说法正确的是(　　) A．∠HBA是△ABC的外角 B．∠HBG是△ABC的外角 C．∠DCE是△ABC的外角 D．∠GBA是△ABC的外角 2．如图，∠A，∠1，∠2的大小关系是(　　) A．∠A＞∠1＞∠2 B．∠2＞∠1＞∠A C．∠A＞∠2＞∠1 D．∠2＞∠A＞∠1 选做题： 3.如图，在五角星图形中， 求：∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数。 【综合拓展类作业】 4.星期天，小明见爸爸愁眉苦脸地在看一张图纸，他便悄悄地来到爸爸身边，想看爸爸为什么犯愁．爸爸见到他，高兴地对他说：“来帮我一个忙，你看这是一个四边形零件的平面图，它要求∠BDC等于140°才算合格．”小明通过测量得∠A＝90°，∠B＝19°，∠C＝40°后就下结论说此零件不合格.于是爸爸让小明解释这是为什么？ 小明很轻松地说出了原因，并用如下的两种方法解出此题．请你代小明分别说出不合格的理由． ①如图(1)，连结AD并延长；②如图(2)，延长CD交AB于E.
课堂总结
作业设计 【知识技能类作业】 必做题： 1．如图，在△ABC中，∠A＝50°，点E，F在AB，AC上，沿EF向内折叠△AEF得到△DEF，则∠1＋∠2等于(　　) A．130° B．120° C．65° D．100° 选做题： 2.证明命题“三角形不共顶点的三个外角的和等于360°”是真命题. 已知：如图，△ABC的三个内角分别为∠1、 ∠2、 ∠3，相对应的外角为∠4、 ∠5、 ∠6. 求证： ∠4+∠5+∠6=360°. 【综合拓展类作业】 　3.AD是△ABC的高，BE平分∠ABC交AD于O，∠BAC＝50°，∠C＝54°.求：∠AEB和∠AOB的度数．
教学反思 课堂小结 1、三角形内角和定理的证明，证明思想是运用辅助线将原三角形处于不同位置的三个内角集中在一起，拼成一个平角.辅助线是联系命题的条件和结论的桥梁，今后我们还要学习它. 2、三角形的外角性质，是由三角形的内角和定理直接推理得到的一个推论.
21世纪教育网(www.21cnjy.com)