1.1 从自然数到有理数 课件(共51张PPT)
文档属性
| 名称 | 1.1 从自然数到有理数 课件(共51张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览











文档简介
1.1 从自然数到有理数
第1章 有理数
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
从自然数到有理数
课程目标
全面了解自然数、整数、分数和有理数的定义和基本特性。
掌握有理数的基本运算方法及其性质。
深入认识有理数在数学中的重要地位及其广泛应用。
自然数的定义和性质
定义:自然数是最基本的数集,从 1 开始,包括所有正整数(在新的定义中,0 也属于自然数)。如 1、2、3、4、5……
特性
唯一性:每个自然数都独一无二。
顺序性:可明确表示事物的先后顺序,如第 1 名、第 2 名等。
封闭性:自然数进行加法和乘法运算,结果仍为自然数。例如 2 + 3 = 5,2 × 3 = 6 。
自然数的应用
计数:生活中计算物体数量,如教室里有 30 张桌子。
排序:比赛排名,如小明在跑步比赛中获得第 5 名。
测量基础:测量长度、重量等时,测量结果常以自然数为基础单位进行记录 。
分数的定义和性质
定义:把单位 “1” 平均分成若干份,表示这样一份或几份的数叫分数。如\(\frac{1}{2}\)、\(\frac{3}{4}\) 。
性质
表示部分与整体关系:如将一个蛋糕平均分成 8 份,其中的 3 份可表示为\(\frac{3}{8}\) 。
分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数(0 除外),分数的大小不变。例如\(\frac{1}{2}=\frac{1×3}{2×3}=\frac{3}{6}\) 。
分数的应用
表示物品的一部分:一根绳子用去了\(\frac{2}{5}\) 。
描述比例关系:在一个班级中,男生占总人数的\(\frac{3}{5}\) 。
数学运算:分数的加、减、乘、除运算在实际问题和数学理论中广泛应用。如\(\frac{1}{2}+\frac{1}{3}=\frac{3 + 2}{6}=\frac{5}{6}\) 。
生活中的相反意义的量
实例
气温的零上 6℃和零下 3℃。
汽车向东行驶 2.5 千米和向西行驶 1.5 千米。
商场盈利 3000 万和亏损 2000 万。
股票指数上涨 100 点或下降 150 点。
特点
意义相反。
属于同一属性,与数值大小无关。
负数的引入
定义:为表示具有相反意义的量,把一种意义的量规定为正,用大于零的数表示,如 123、3.14 等,这样的数叫正数;把另一种与之意义相反的量规定为负,用大于 0 的数前面放上 “-”(读作负号)来表示,如 - 1、-2.5 等,这样的数叫做负数。
注意:0 既不是正数,也不是负数。
有理数的定义
有理数是能够表示为两个整数之比的数,包括整数和分数。整数可看作分母为 1 的分数。如 2 可表示为\(\frac{2}{1}\),-3 可表示为\(\frac{-3}{1}\),\(\frac{1}{2}\) 。
有理数的分类
按定义分类
整数:正整数、零、负整数统称整数。如 1、0、-1。
分数:正分数、负分数统称分数。如\(\frac{1}{2}\)、\(-\frac{3}{4}\) 。
按性质分类
正有理数:正整数和正分数。如 2、\(\frac{3}{5}\) 。
零:既不是正数也不是负数。
负有理数:负整数和负分数。如 - 3、\(-\frac{2}{3}\) 。
有理数的应用
测量与计算:生活中测量长度、重量、时间等,结果常用有理数表示。如铅笔长 15.5 厘米,即\(\frac{31}{2}\)厘米 。
金融领域:利率、股票价格、汇率等常用有理数表示。如年利率为 3.5%,即\(\frac{3.5}{100}\) 。
工程与科学:物理中的速度、加速度,工程中的比例尺等计算都离不开有理数。如汽车速度为 60 千米 / 小时,即\(\frac{60}{1}\)千米 / 小时 。
总结
数的发展:从自然数到分数,再到引入负数形成有理数。
重要概念:自然数、分数、负数、有理数的定义和性质。
有理数分类:按定义和性质两种分类方式。
应用广泛:在生活、金融、科学等多领域有重要应用。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.自然数的作用:
(1)计数,计量人或物的数量;
(2)测量,如长度、高度、质量等;
(3)标号或排序,如城市的公共汽车路线、门牌号码、邮编、身
份证号码等。
并不是所有的小数都能化为分数,如小学学过的π 就不能
化为分数。
?
典例1 李亮收集到以下信息:
(1)某城市有16条公共汽车线路;
(2)王刚乘坐T26 次火车去上海;
?
(3)刘风在校运动会上获得跳远比赛第1名。
其中,用自然数表示标号的有_______,表示排序的有_______,表
示计数的有_______。(填序号)
(2)
(3)
(1)
2.分数、小数的关系:
(1)分数可以看作两个整数相除,因此分数都可以化为小数
(有限小数或无限循环小数);
(2)有限小数、无限循环小数都可以化为分数。如
1.68=168100=4225,0.3?=13,20%=15 。
?
典例2 把下列各数化成分数:
2.7,0.13,12% 。
?
解:2.7=2710,0.13=13100,12%=12100=325 。
?
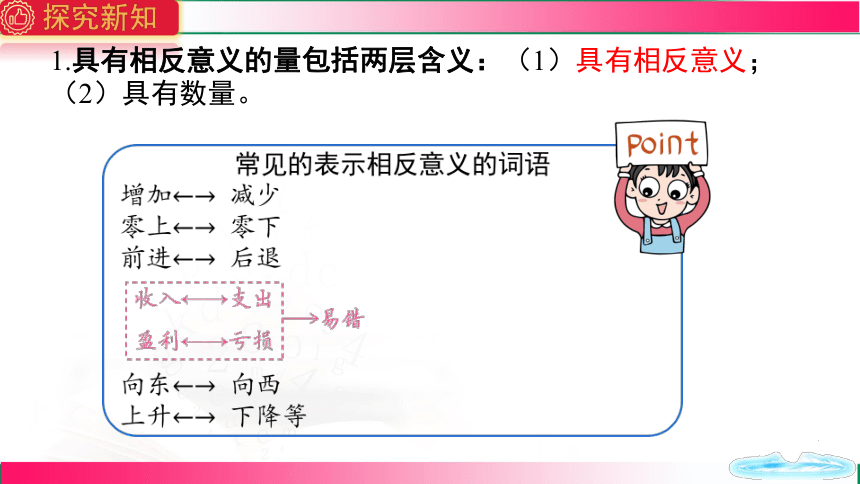
1.具有相反意义的量包括两层含义:(1)具有相反意义;
(2)具有数量。
常见的表示相反意义的词语
增加←→ 减少
零上←→ 零下
前进←→ 后退
向东←→ 向西
上升←→ 下降等
?
(2)具有数量。
敲黑板 具有相反意义的量的特点
特点
解读与举例
成对性
单独一个量不能成为具有相反意义的量,如上升10米。
同类性
具有相反意义的量必须是同类量,如向东走20米与盈利20元就不是具有相反意义的量。
不唯
一性
具有相反意义的量,不要求数量相等,如与盈利300元具有相反意义的量不唯一,可以是亏损400元,也可以是亏损100元等。
典例3 下列选项中,是具有相反意义的量的是( )
C
A.身高增加1?cm与体重减少1?kg
B.海平面以上与海平面以下
C.向东5?m与向西8?m
D.存入100元与降价10元
?
2.具有相反意义的量的表示
为了区别具有相反意义的量,通常把一种意义的量用以前学
过的数或者带有“+ ”(正号)的数表示;把另外一种与它意义
相反的量用带有“-”(负号)的数表示。
表示具有相反意义的量时,一定要说明数量和单位。
?
典例4(1) 2024年4月25日20时59分,搭载
神舟十八号载人飞船的长征二号F 遥十八运载火箭在酒泉卫星发射
中心成功发射。若运载火箭发射点火前5秒记为?5 秒,那么运载火
箭发射点火后10秒记作_____________________。
?
+10秒(注意带单位)
?
(2)如果某蓄水池的水位比标准水位高2米,记作+2 米,那么比
标准水位低0.5米,应记作________;恰好等于标准水位,应记作
_____。
?
?0.5米
?
0米
(3)手机移动支付给生活带来便捷,若规定收款为正,则+37 元
表示__________,?111 元表示___________。
?
收款37元
付款111元
(4)从山脚测山高为300?m,山脚高出海平面50?m 。若以海平面
为基准,山脚的高度记作+50?m ,则山高记作________;若以山脚
为基准,山高记作+300?m ,则海平面的高度记作_______。
(选择的基准不同,表示的结果也不同)
?
+350?m
?
?50?m
?
解题通法
用正数、负数表示具有相反意义的量的步骤
数的
分类
定义
举例
注意
正数
大于零的数。
123,13,1.31
正数前的“+ ”
常省略不写。
负数
用大于零的数前面放
上负号“-”来表示的
数。
?60,?0.5,?23
负数前的“-”不
能省略不写。
数的
分类
定义
举例
注意
正数
大于零的数。
负数
用大于零的数前面放
上负号“-”来表示的
数。
负数前的“-”不
能省略不写。
数的
分类
定义
举例
注意
0
(1)0是正数与负数的分界;
(2)0不仅可以表示“没有”,还可以表示
某种量的基准,如0?℃ 表示实际温度为冰
点时的计量结果。
0既不是正数,也不是负数。
数的
分类
定义
举例
注意
0
0既不是正数,也不是负数。
典例5 (宁波镇海区校级期中)下列各数?1,2,?3,0,π 中,
负数有( )
?
B
A.1个 B.2个 C.3个 D.4个
解析:用大于零的数前面放上负号“-”来表示的数叫作负数,
所以?1,?3 这两个数是负数。
?
1.整数:正整数、零和负整数统称整数,如?3,?2,?1 ,0,
1,2,3等。
整数分为奇数和偶数。奇数和偶数中也有负数,如?6 ,
?4,?2是偶数,?5,?3,?1 是奇数。
2.分数:正分数、负分数统称分数,如213,0.2,?1.25,?15 等。
3.有理数:整数和分数统称有理数。
(任何一个有理数都可以写成????????(????,????是整数,????≠0)的形式)
?
教材延伸
4.部分常用的数:
(1)正整数:如1,2,3,? 。
负整数:如?1,?2,?3,? 。
(2)正分数:如12,43,0.1,5.32,0.3?,? 。
负分数:如?13,?65,?0.1,?5.32,?0.3? ,…。
(3)非负数:正数和0。
非正数:负数和0。
非负整数:正整数和0。(即自然数)
?
典例6 下列说法正确的有( )
①不带负号的数都是正数;②正数、负数统称有理数;
③?3.14 既是负分数,也是有理数;④有理数中除了
正数就是负数。
?
B
A.0个 B.1个 C.2个 D.3个
解析:
序号
分析
判断
①
不带负号的数包括0,但0既不是正数也不是负数。
×
②
整数和分数统称有理数。
×
③
?3.14 既是负分数,也是有理数。
√
④
0是有理数,但0既不是正数也不是负数。
×
序号
分析
判断
①
不带负号的数包括0,但0既不是正数也不是负数。
②
整数和分数统称有理数。
③
√
④
0是有理数,但0既不是正数也不是负数。
故说法正确的只有1个。
1.按定义分类
2.按性质符号分类
敲黑板 有理数的分类三原则
(1)分类不重合——所分的各类应互不包含,如有理
数分为非负有理数、零和正有理数就违反了这一原则;
(2)分类无遗漏——所分各类之“和”必须是原来的全部,如
将有理数分为正有理数和负有理数就漏掉了0;
(3)标准要统一——必须按同一分类标准进行分类,如将有
理数分为正有理数、零和负分数,分类标准就不统一。
典例7 把下列各数填在相应的横线上。
+203,0,+6.4,?9,?57,2.6,?0.1 。
正整数:_ _;
负分数:_ _;
非正数:_ _;
有理数:_ _。
?
在典例7的条件下。
负整数:________;
正分数:________;
非负数:___ _____;
自然数:________。
+6.4,2.6
-9
+203,0
+203,0,+6.4,2.6
自然数及其应用
1. 一个长26厘米、宽19厘米、高0.7厘米的物体,最有可能
是( B )
A. 衣柜
B. 数学课本
C. 手机
D. 橡皮
B
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 小亮在看报纸时,收集到下列信息:①某地的国民生产总
值位列全国第5位;②某城市有16条公共汽车路线;③小
刚乘G56次高铁去北京;④小凤在校运会上获得跳远比赛
第1名.其中的数表示标号或排序的是( C )
A. ①②③
B. ①②④
C. ①③④
D. ②③④
C
1
2
3
4
5
6
7
8
9
10
11
12
13
3. [新考向·身边的数学]火车票上的车次号有两个意义,一是
数字越小表示车速越快,1~98次为特快列车,101~198
次为直快列车,301~398次为普快列车,401~498次为普
客列车;二是单数与双数表示不同的行驶方向,其中单数
表示从北京开出,双数表示开往北京.根据以上规定,杭
州开往北京的某一直快列车的车次号可能是( C )
A. 20
B. 119
C. 138
D. 319
C
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 一场演唱会的观众席是一个长100米、宽50米的长方形场
地,演唱会的门票全部卖光,观众席里站满了歌迷.下面
最有可能是参加演唱会的观众总人数的是( C )
A. 1 000
B. 2 000
C. 20 000
D. 100 000
C
1
2
3
4
5
6
7
8
9
10
11
12
13
5. [新考向·地域文化]下面关于六和塔的描述用了很多
数,说说它们哪些属于计数?哪些属于测量?哪些属
于标号或排序?
1
2
3
4
5
6
7
8
9
10
11
12
13
六和塔位于西湖之南,钱塘江畔月轮山腰上.北宋开宝三
年(公元970年),当时杭州为吴越国国都,国王为镇住钱
塘江潮水派人建造了六和塔.现在的六和塔塔身重建于南
宋,取佛教“六和敬”之义,命名为六和塔.塔高约60
米,其建造风格非常独特,塔内部砖石结构分7层,外部
木结构为8面13层.1961年被国务院定为全国重点文物保护
单位.
1
2
3
4
5
6
7
8
9
10
11
12
13
【解】属于计数的有:7,8,13;
属于测量的有:60;
属于标号或排序的有:970,1 961.
1
2
3
4
5
6
7
8
9
10
11
12
13
分数与小数的转化
6. 下列分数中,能化成有限小数的是( C )
A. ????????
B. ????????????
C. ????????????
D. ????????????
C
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 将下列小数化为分数,分数化为小数.
(1)0.32 (2)4.28 (3)7.2 (4)0.625
【解】(1)0.32=???????????? ;
(2)4.28=4???????????? ;
?
(3)7.2=7???????? ;
(4)0.625=???????? ;
?
1
2
3
4
5
6
7
8
9
10
11
12
13
(5)???????? (6)3???????? (7)???????????????? (8)????????????
?
(5)???????? =0.75;
?
(6)3???????? =3.875;
(7)???????????????? =0.68;
?
(8)???????????? =1.8????· .
?
1
2
3
4
5
6
7
8
9
10
11
12
13
小数、分数的应用
8. 我们把分子为1的分数叫作单位分数.如???????? ,???????? ,???????? ,…,
任何一个单位分数都可以拆分成两个不同单位分数的和,
如???????? =???????? +???????? ,???????? =???????? +???????????? ,???????? =???????? +???????????? ,….
?
(1)根据对上述式子的观察,你会发现???????? =????□ +????〇 ,则□
所表示的数为 ,〇所表示的数为 ?;
?
(2)进一步思考,单位分数???????? =????△ +????☆ (n是不小于2的自然
数),则△所表示的式子为 ,☆所表示的式子
为 ?.
?
6
30
n+1
n(n+1)
1
2
3
4
5
6
7
8
9
10
11
12
13
9. [新考向·传统文化 2024·浙江台州调研]《礼记·杂记上》记
载:“苇席以为屋,蒲席以为裳帷.”蒲为多年生草本植
物,生池沼中,高近2米,根茎长在泥里,可食.其中涉及
的自然数2属于( B )
A. 计数
B. 测量
C. 标号
D. 排序
B
1
2
3
4
5
6
7
8
9
10
11
12
13
10. [2023·金华义乌月考]按一定规律排列的一列数依次为:
???????? ,???????? ,???????????? ,???????????? ,???????????? ,???????????? ,…,按此规律排列下去,这
列数中的第9个数是 ?.
?
????????????
?
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)5名成人,5名儿童,选择哪种方案合算?
【解】方案一:5×150+5×60=1 050(元),
方案二:(5+5)×100=1 000(元),
1 050>1 000,因此选择方案二合算.
11. 如图,某旅行社推出了“西湖风景区一日游”的两种价
格方案.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)5名成人,10名儿童,怎样购票合算?
【解】5名成人选方案二,10名儿童选方案一购票
合算.
1
2
3
4
5
6
7
8
9
10
11
12
13
12. [母题 教材P8作业题T1]读完下面这段话,回答问题:
我们的教室长12 m,宽8 m,讲台长1.2 m,宽0.8 m,我们班有50人,占全年级人数的8%,多数同学都是13岁.
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)在老师刚才描述中出现了哪些数?其中哪些属于计
数?哪些属于测量?哪些属于标号或排序?
【解】在老师刚才描述中出现了:12、8、1.2、
0.8、50、8%、13,其中属于计数的有50、8%、
13,属于测量的有12、8、1.2、0.8,出现的数均不
属于标号或排序;
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)你能将这些数进行分类吗?
【解】能.按整数和分数分类:整数有12、8、50、
13,分数有1.2、0.8、8%;
1
2
3
4
5
6
7
8
9
10
11
12
13
(3)在实际生活中仅有整数和分数够用吗?请你举例
说明.
【解】仅有整数和分数不够用,例如求圆的周长和面
积时,发现圆周率,但圆周率的值并不能由两个整数
相除而得;又如求边长为1的正方形对角线长时,求
得的既不是整数也不是分数.(举例不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [新考法·阅读类比法]阅读材料:把无限循环小数化为分
数,可以按如下方法进行:
以0.????· 为例,令0.????· =x,
由0.????· =0.333…,可知10x=3.333…,所以10x=3+
x,解得x=???????? ,于是0.????· =???????? .
?
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)请把无限循环小数0.????· 化为分数是 ?;
(2)请把无限循环小数0.????????· 化为分数;
?
【解】令0.????????· =x,则100x=75.757 5…,
所以100x=75+x,所以x=???????????????? .
?
????????
?
(3)将0.????· 1????· 与0.????· 的积化为小数,则小数点后第999位
数字是 ?.
?
0
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
第1章 有理数
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
从自然数到有理数
课程目标
全面了解自然数、整数、分数和有理数的定义和基本特性。
掌握有理数的基本运算方法及其性质。
深入认识有理数在数学中的重要地位及其广泛应用。
自然数的定义和性质
定义:自然数是最基本的数集,从 1 开始,包括所有正整数(在新的定义中,0 也属于自然数)。如 1、2、3、4、5……
特性
唯一性:每个自然数都独一无二。
顺序性:可明确表示事物的先后顺序,如第 1 名、第 2 名等。
封闭性:自然数进行加法和乘法运算,结果仍为自然数。例如 2 + 3 = 5,2 × 3 = 6 。
自然数的应用
计数:生活中计算物体数量,如教室里有 30 张桌子。
排序:比赛排名,如小明在跑步比赛中获得第 5 名。
测量基础:测量长度、重量等时,测量结果常以自然数为基础单位进行记录 。
分数的定义和性质
定义:把单位 “1” 平均分成若干份,表示这样一份或几份的数叫分数。如\(\frac{1}{2}\)、\(\frac{3}{4}\) 。
性质
表示部分与整体关系:如将一个蛋糕平均分成 8 份,其中的 3 份可表示为\(\frac{3}{8}\) 。
分数的基本性质:分数的分子和分母同时乘或者除以一个相同的数(0 除外),分数的大小不变。例如\(\frac{1}{2}=\frac{1×3}{2×3}=\frac{3}{6}\) 。
分数的应用
表示物品的一部分:一根绳子用去了\(\frac{2}{5}\) 。
描述比例关系:在一个班级中,男生占总人数的\(\frac{3}{5}\) 。
数学运算:分数的加、减、乘、除运算在实际问题和数学理论中广泛应用。如\(\frac{1}{2}+\frac{1}{3}=\frac{3 + 2}{6}=\frac{5}{6}\) 。
生活中的相反意义的量
实例
气温的零上 6℃和零下 3℃。
汽车向东行驶 2.5 千米和向西行驶 1.5 千米。
商场盈利 3000 万和亏损 2000 万。
股票指数上涨 100 点或下降 150 点。
特点
意义相反。
属于同一属性,与数值大小无关。
负数的引入
定义:为表示具有相反意义的量,把一种意义的量规定为正,用大于零的数表示,如 123、3.14 等,这样的数叫正数;把另一种与之意义相反的量规定为负,用大于 0 的数前面放上 “-”(读作负号)来表示,如 - 1、-2.5 等,这样的数叫做负数。
注意:0 既不是正数,也不是负数。
有理数的定义
有理数是能够表示为两个整数之比的数,包括整数和分数。整数可看作分母为 1 的分数。如 2 可表示为\(\frac{2}{1}\),-3 可表示为\(\frac{-3}{1}\),\(\frac{1}{2}\) 。
有理数的分类
按定义分类
整数:正整数、零、负整数统称整数。如 1、0、-1。
分数:正分数、负分数统称分数。如\(\frac{1}{2}\)、\(-\frac{3}{4}\) 。
按性质分类
正有理数:正整数和正分数。如 2、\(\frac{3}{5}\) 。
零:既不是正数也不是负数。
负有理数:负整数和负分数。如 - 3、\(-\frac{2}{3}\) 。
有理数的应用
测量与计算:生活中测量长度、重量、时间等,结果常用有理数表示。如铅笔长 15.5 厘米,即\(\frac{31}{2}\)厘米 。
金融领域:利率、股票价格、汇率等常用有理数表示。如年利率为 3.5%,即\(\frac{3.5}{100}\) 。
工程与科学:物理中的速度、加速度,工程中的比例尺等计算都离不开有理数。如汽车速度为 60 千米 / 小时,即\(\frac{60}{1}\)千米 / 小时 。
总结
数的发展:从自然数到分数,再到引入负数形成有理数。
重要概念:自然数、分数、负数、有理数的定义和性质。
有理数分类:按定义和性质两种分类方式。
应用广泛:在生活、金融、科学等多领域有重要应用。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.自然数的作用:
(1)计数,计量人或物的数量;
(2)测量,如长度、高度、质量等;
(3)标号或排序,如城市的公共汽车路线、门牌号码、邮编、身
份证号码等。
并不是所有的小数都能化为分数,如小学学过的π 就不能
化为分数。
?
典例1 李亮收集到以下信息:
(1)某城市有16条公共汽车线路;
(2)王刚乘坐T26 次火车去上海;
?
(3)刘风在校运动会上获得跳远比赛第1名。
其中,用自然数表示标号的有_______,表示排序的有_______,表
示计数的有_______。(填序号)
(2)
(3)
(1)
2.分数、小数的关系:
(1)分数可以看作两个整数相除,因此分数都可以化为小数
(有限小数或无限循环小数);
(2)有限小数、无限循环小数都可以化为分数。如
1.68=168100=4225,0.3?=13,20%=15 。
?
典例2 把下列各数化成分数:
2.7,0.13,12% 。
?
解:2.7=2710,0.13=13100,12%=12100=325 。
?
1.具有相反意义的量包括两层含义:(1)具有相反意义;
(2)具有数量。
常见的表示相反意义的词语
增加←→ 减少
零上←→ 零下
前进←→ 后退
向东←→ 向西
上升←→ 下降等
?
(2)具有数量。
敲黑板 具有相反意义的量的特点
特点
解读与举例
成对性
单独一个量不能成为具有相反意义的量,如上升10米。
同类性
具有相反意义的量必须是同类量,如向东走20米与盈利20元就不是具有相反意义的量。
不唯
一性
具有相反意义的量,不要求数量相等,如与盈利300元具有相反意义的量不唯一,可以是亏损400元,也可以是亏损100元等。
典例3 下列选项中,是具有相反意义的量的是( )
C
A.身高增加1?cm与体重减少1?kg
B.海平面以上与海平面以下
C.向东5?m与向西8?m
D.存入100元与降价10元
?
2.具有相反意义的量的表示
为了区别具有相反意义的量,通常把一种意义的量用以前学
过的数或者带有“+ ”(正号)的数表示;把另外一种与它意义
相反的量用带有“-”(负号)的数表示。
表示具有相反意义的量时,一定要说明数量和单位。
?
典例4(1) 2024年4月25日20时59分,搭载
神舟十八号载人飞船的长征二号F 遥十八运载火箭在酒泉卫星发射
中心成功发射。若运载火箭发射点火前5秒记为?5 秒,那么运载火
箭发射点火后10秒记作_____________________。
?
+10秒(注意带单位)
?
(2)如果某蓄水池的水位比标准水位高2米,记作+2 米,那么比
标准水位低0.5米,应记作________;恰好等于标准水位,应记作
_____。
?
?0.5米
?
0米
(3)手机移动支付给生活带来便捷,若规定收款为正,则+37 元
表示__________,?111 元表示___________。
?
收款37元
付款111元
(4)从山脚测山高为300?m,山脚高出海平面50?m 。若以海平面
为基准,山脚的高度记作+50?m ,则山高记作________;若以山脚
为基准,山高记作+300?m ,则海平面的高度记作_______。
(选择的基准不同,表示的结果也不同)
?
+350?m
?
?50?m
?
解题通法
用正数、负数表示具有相反意义的量的步骤
数的
分类
定义
举例
注意
正数
大于零的数。
123,13,1.31
正数前的“+ ”
常省略不写。
负数
用大于零的数前面放
上负号“-”来表示的
数。
?60,?0.5,?23
负数前的“-”不
能省略不写。
数的
分类
定义
举例
注意
正数
大于零的数。
负数
用大于零的数前面放
上负号“-”来表示的
数。
负数前的“-”不
能省略不写。
数的
分类
定义
举例
注意
0
(1)0是正数与负数的分界;
(2)0不仅可以表示“没有”,还可以表示
某种量的基准,如0?℃ 表示实际温度为冰
点时的计量结果。
0既不是正数,也不是负数。
数的
分类
定义
举例
注意
0
0既不是正数,也不是负数。
典例5 (宁波镇海区校级期中)下列各数?1,2,?3,0,π 中,
负数有( )
?
B
A.1个 B.2个 C.3个 D.4个
解析:用大于零的数前面放上负号“-”来表示的数叫作负数,
所以?1,?3 这两个数是负数。
?
1.整数:正整数、零和负整数统称整数,如?3,?2,?1 ,0,
1,2,3等。
整数分为奇数和偶数。奇数和偶数中也有负数,如?6 ,
?4,?2是偶数,?5,?3,?1 是奇数。
2.分数:正分数、负分数统称分数,如213,0.2,?1.25,?15 等。
3.有理数:整数和分数统称有理数。
(任何一个有理数都可以写成????????(????,????是整数,????≠0)的形式)
?
教材延伸
4.部分常用的数:
(1)正整数:如1,2,3,? 。
负整数:如?1,?2,?3,? 。
(2)正分数:如12,43,0.1,5.32,0.3?,? 。
负分数:如?13,?65,?0.1,?5.32,?0.3? ,…。
(3)非负数:正数和0。
非正数:负数和0。
非负整数:正整数和0。(即自然数)
?
典例6 下列说法正确的有( )
①不带负号的数都是正数;②正数、负数统称有理数;
③?3.14 既是负分数,也是有理数;④有理数中除了
正数就是负数。
?
B
A.0个 B.1个 C.2个 D.3个
解析:
序号
分析
判断
①
不带负号的数包括0,但0既不是正数也不是负数。
×
②
整数和分数统称有理数。
×
③
?3.14 既是负分数,也是有理数。
√
④
0是有理数,但0既不是正数也不是负数。
×
序号
分析
判断
①
不带负号的数包括0,但0既不是正数也不是负数。
②
整数和分数统称有理数。
③
√
④
0是有理数,但0既不是正数也不是负数。
故说法正确的只有1个。
1.按定义分类
2.按性质符号分类
敲黑板 有理数的分类三原则
(1)分类不重合——所分的各类应互不包含,如有理
数分为非负有理数、零和正有理数就违反了这一原则;
(2)分类无遗漏——所分各类之“和”必须是原来的全部,如
将有理数分为正有理数和负有理数就漏掉了0;
(3)标准要统一——必须按同一分类标准进行分类,如将有
理数分为正有理数、零和负分数,分类标准就不统一。
典例7 把下列各数填在相应的横线上。
+203,0,+6.4,?9,?57,2.6,?0.1 。
正整数:_ _;
负分数:_ _;
非正数:_ _;
有理数:_ _。
?
在典例7的条件下。
负整数:________;
正分数:________;
非负数:___ _____;
自然数:________。
+6.4,2.6
-9
+203,0
+203,0,+6.4,2.6
自然数及其应用
1. 一个长26厘米、宽19厘米、高0.7厘米的物体,最有可能
是( B )
A. 衣柜
B. 数学课本
C. 手机
D. 橡皮
B
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 小亮在看报纸时,收集到下列信息:①某地的国民生产总
值位列全国第5位;②某城市有16条公共汽车路线;③小
刚乘G56次高铁去北京;④小凤在校运会上获得跳远比赛
第1名.其中的数表示标号或排序的是( C )
A. ①②③
B. ①②④
C. ①③④
D. ②③④
C
1
2
3
4
5
6
7
8
9
10
11
12
13
3. [新考向·身边的数学]火车票上的车次号有两个意义,一是
数字越小表示车速越快,1~98次为特快列车,101~198
次为直快列车,301~398次为普快列车,401~498次为普
客列车;二是单数与双数表示不同的行驶方向,其中单数
表示从北京开出,双数表示开往北京.根据以上规定,杭
州开往北京的某一直快列车的车次号可能是( C )
A. 20
B. 119
C. 138
D. 319
C
1
2
3
4
5
6
7
8
9
10
11
12
13
4. 一场演唱会的观众席是一个长100米、宽50米的长方形场
地,演唱会的门票全部卖光,观众席里站满了歌迷.下面
最有可能是参加演唱会的观众总人数的是( C )
A. 1 000
B. 2 000
C. 20 000
D. 100 000
C
1
2
3
4
5
6
7
8
9
10
11
12
13
5. [新考向·地域文化]下面关于六和塔的描述用了很多
数,说说它们哪些属于计数?哪些属于测量?哪些属
于标号或排序?
1
2
3
4
5
6
7
8
9
10
11
12
13
六和塔位于西湖之南,钱塘江畔月轮山腰上.北宋开宝三
年(公元970年),当时杭州为吴越国国都,国王为镇住钱
塘江潮水派人建造了六和塔.现在的六和塔塔身重建于南
宋,取佛教“六和敬”之义,命名为六和塔.塔高约60
米,其建造风格非常独特,塔内部砖石结构分7层,外部
木结构为8面13层.1961年被国务院定为全国重点文物保护
单位.
1
2
3
4
5
6
7
8
9
10
11
12
13
【解】属于计数的有:7,8,13;
属于测量的有:60;
属于标号或排序的有:970,1 961.
1
2
3
4
5
6
7
8
9
10
11
12
13
分数与小数的转化
6. 下列分数中,能化成有限小数的是( C )
A. ????????
B. ????????????
C. ????????????
D. ????????????
C
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 将下列小数化为分数,分数化为小数.
(1)0.32 (2)4.28 (3)7.2 (4)0.625
【解】(1)0.32=???????????? ;
(2)4.28=4???????????? ;
?
(3)7.2=7???????? ;
(4)0.625=???????? ;
?
1
2
3
4
5
6
7
8
9
10
11
12
13
(5)???????? (6)3???????? (7)???????????????? (8)????????????
?
(5)???????? =0.75;
?
(6)3???????? =3.875;
(7)???????????????? =0.68;
?
(8)???????????? =1.8????· .
?
1
2
3
4
5
6
7
8
9
10
11
12
13
小数、分数的应用
8. 我们把分子为1的分数叫作单位分数.如???????? ,???????? ,???????? ,…,
任何一个单位分数都可以拆分成两个不同单位分数的和,
如???????? =???????? +???????? ,???????? =???????? +???????????? ,???????? =???????? +???????????? ,….
?
(1)根据对上述式子的观察,你会发现???????? =????□ +????〇 ,则□
所表示的数为 ,〇所表示的数为 ?;
?
(2)进一步思考,单位分数???????? =????△ +????☆ (n是不小于2的自然
数),则△所表示的式子为 ,☆所表示的式子
为 ?.
?
6
30
n+1
n(n+1)
1
2
3
4
5
6
7
8
9
10
11
12
13
9. [新考向·传统文化 2024·浙江台州调研]《礼记·杂记上》记
载:“苇席以为屋,蒲席以为裳帷.”蒲为多年生草本植
物,生池沼中,高近2米,根茎长在泥里,可食.其中涉及
的自然数2属于( B )
A. 计数
B. 测量
C. 标号
D. 排序
B
1
2
3
4
5
6
7
8
9
10
11
12
13
10. [2023·金华义乌月考]按一定规律排列的一列数依次为:
???????? ,???????? ,???????????? ,???????????? ,???????????? ,???????????? ,…,按此规律排列下去,这
列数中的第9个数是 ?.
?
????????????
?
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)5名成人,5名儿童,选择哪种方案合算?
【解】方案一:5×150+5×60=1 050(元),
方案二:(5+5)×100=1 000(元),
1 050>1 000,因此选择方案二合算.
11. 如图,某旅行社推出了“西湖风景区一日游”的两种价
格方案.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)5名成人,10名儿童,怎样购票合算?
【解】5名成人选方案二,10名儿童选方案一购票
合算.
1
2
3
4
5
6
7
8
9
10
11
12
13
12. [母题 教材P8作业题T1]读完下面这段话,回答问题:
我们的教室长12 m,宽8 m,讲台长1.2 m,宽0.8 m,我们班有50人,占全年级人数的8%,多数同学都是13岁.
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)在老师刚才描述中出现了哪些数?其中哪些属于计
数?哪些属于测量?哪些属于标号或排序?
【解】在老师刚才描述中出现了:12、8、1.2、
0.8、50、8%、13,其中属于计数的有50、8%、
13,属于测量的有12、8、1.2、0.8,出现的数均不
属于标号或排序;
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)你能将这些数进行分类吗?
【解】能.按整数和分数分类:整数有12、8、50、
13,分数有1.2、0.8、8%;
1
2
3
4
5
6
7
8
9
10
11
12
13
(3)在实际生活中仅有整数和分数够用吗?请你举例
说明.
【解】仅有整数和分数不够用,例如求圆的周长和面
积时,发现圆周率,但圆周率的值并不能由两个整数
相除而得;又如求边长为1的正方形对角线长时,求
得的既不是整数也不是分数.(举例不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [新考法·阅读类比法]阅读材料:把无限循环小数化为分
数,可以按如下方法进行:
以0.????· 为例,令0.????· =x,
由0.????· =0.333…,可知10x=3.333…,所以10x=3+
x,解得x=???????? ,于是0.????· =???????? .
?
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)请把无限循环小数0.????· 化为分数是 ?;
(2)请把无限循环小数0.????????· 化为分数;
?
【解】令0.????????· =x,则100x=75.757 5…,
所以100x=75+x,所以x=???????????????? .
?
????????
?
(3)将0.????· 1????· 与0.????· 的积化为小数,则小数点后第999位
数字是 ?.
?
0
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
