1.3 绝对值 课件（共33张PPT）

(共33张PPT)
1.3 绝对值
第1章 有理数
【2025-2026学年】浙教版 数学 七年级上册
授课教师：********
班 级：********
时 间：********
绝对值
课程目标
理解绝对值的概念，掌握绝对值的几何意义和代数意义。
能够熟练计算一个数的绝对值。
学会利用绝对值解决实际问题及比较数的大小。
绝对值的定义
几何意义
在数轴上，一个数所对应的点与原点的距离叫做这个数的绝对值。例如，在数轴上表示数 3 的点与原点的距离是 3，所以 3 的绝对值是 3；表示数 - 3 的点与原点的距离也是 3，所以 - 3 的绝对值是 3。
代数意义
一个正数的绝对值是它本身。比如，|5|=5。
一个负数的绝对值是它的相反数。例如，|-4|=4。
0 的绝对值是 0，即 | 0|=0。
绝对值的表示方法
一个数 a 的绝对值记作 | a|。如 + 2 的绝对值记作 |+2|，-3 的绝对值记作 |-3|。
绝对值的性质
任何有理数的绝对值都是非负数，即 | a|≥0。
若 | a|=|b|，则 a=b 或 a=-b。例如，|2|=| -2 |，此时 2 和 - 2 互为相反数。
若 a 为有理数，则 | a|=|-a|。比如，|3|=| -3 |=3。
绝对值的计算
对于正数，直接去掉绝对值符号，结果就是其本身。如 | 7|=7。
对于负数，去掉绝对值符号后，结果是它的相反数。如 |-6|=6。
0 的绝对值是 0，即 | 0|=0。
利用绝对值比较两个负数的大小
两个负数比较大小，绝对值大的反而小。例如，比较 - 5 和 - 3 的大小：
先求出它们的绝对值，| -5 |=5，| -3 |=3。
因为 5＞3，所以 - 5＜-3。
绝对值的应用
实际距离计算：在数轴上，两点之间的距离可以用这两个数的绝对值的差或和来表示。比如，数轴上表示 3 和 - 2 的两点之间的距离是 | 3 - (-2)|=|3 + 2|=5。
表示误差范围：在生产中，产品的尺寸往往有一定的误差范围，通常用绝对值来表示。例如，某零件的标准长度是 50mm，允许的误差范围是 ±0.5mm，即长度 x 满足 | x - 50|≤0.5mm。
判断数的正负性相关问题：若 | a|=a，则 a 是非负数；若 | a|=-a，则 a 是非正数。
课堂练习
计算下列各数的绝对值：|+9|、|-12|、|0|、| -3.5 |。
比较下列各组数的大小：
-8 和 - 6
-\(\frac{3}{4}\)和 -\(\frac{2}{3}\)
已知 | x|=5，求 x 的值。
总结
绝对值的几何意义是数轴上数对应的点到原点的距离，代数意义要根据数的正负性来确定。
绝对值具有非负性，计算时要根据数的正负正确去掉绝对值符号。
利用绝对值可以比较两个负数的大小，也能解决实际生活中的一些距离、误差等问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.借助数轴理解绝对值的意义,体会数形结合的思想方法。
2.掌握求有理数的绝对值的方法。
3.掌握绝对值的性质。
4.会利用绝对值解决简单的问题,培养应用意识。
1.绝对值的概念：把一个数在数轴上对应的点到原点的距离
叫作这个数的绝对值。（由于绝对值是距离，所以绝对值具
有非负性）
2.表示方法：一个数的绝对值表示为，读作“ 的绝对值”。
一个数在数轴上对应的点到原点的距离越远，
绝对值越大；到原点的距离越近，绝对值越小。反之
也成立。（绝对值最小的数是0）
3.绝对值的性质
（1）一个正数的绝对值是它本身；一个负数的绝对值是它的
相反数；零的绝对值是零。
①如果，那么 ；
②如果，那么；简记为
③如果，那么 。
（2）互为相反数的两个数的绝对值相等。即若, 互为
相反数，则。（拓展：任何数的绝对值都不小于
它本身，即 ）
教材延伸
（1）绝对值是它本身的数是非负数，即若，则 ；
绝对值是其相反数的数是非正数，即若，则 。
（2）绝对值是某个正数的数有两个，它们互为相反数，即若
，则，如，则 。
（3）若两个数的绝对值相等，则这两个数相等或互为相反数，
即若,则或 。
典例1 求下列各数的绝对值：
6，,，， 。
解：,，，，
。
知识过关
①一个数在数轴上对应的点到原点的 　距离　叫作这个数的绝对值.
②一个正数的绝对值是 　它本身　；一个负数的绝对值是 　它的相反数　；0的绝对值是 　0　.
③互为相反数的两个数的绝对值 　相等　.
距离
它本身
它
的相反数
0
相等
绝对值的概念
1. －6的绝对值是(　A　)
A. 6
D. －6
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
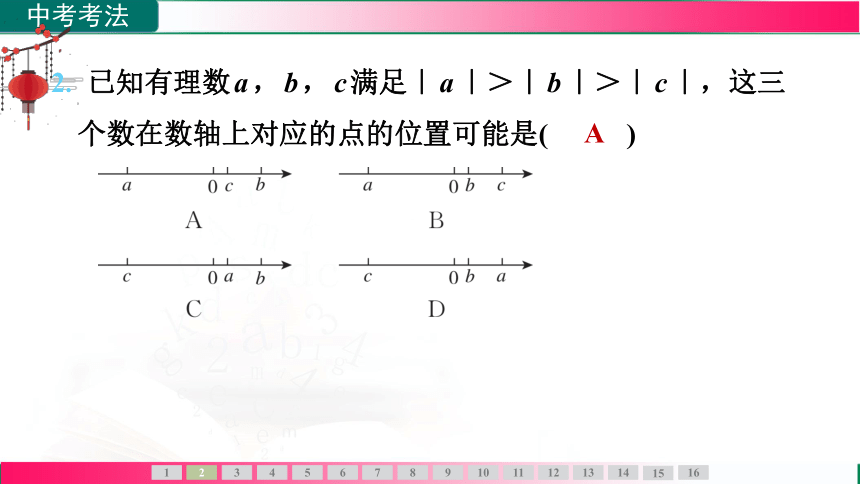
2. 已知有理数a，b，c满足｜a｜＞｜b｜＞｜c｜，这三
个数在数轴上对应的点的位置可能是(　A　)
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3. 在数轴上，下列数表示的点离原点最远的是(　A　)
A. －2 024 B. 2 004
C. －2 000 D. 2 023
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
绝对值的性质
4. [2023·台州黄岩区期末]已知｜a｜＝｜－2｜，则a等于
(　D　)
A. 2 B. －2
C. 0 D. ±2
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5. 下列说法不正确的是(　C　)
A. 任意一个有理数的绝对值不一定是正数
B. 负数的绝对值是它的相反数
C. 如果两个数的绝对值相等，那么这两个数相等
D. 0的绝对值是0
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6. [2024·衢州模拟]用符号语言表述“负数的绝对值等于它的
相反数”正确的是(　D　)
A. ｜－a｜＝a
B. ｜a｜＝－a
C. ｜－a｜＝a(a＜0)
D. ｜a｜＝－a(a＜0)
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 一个数具有以下两个特点：①它的绝对值等于3；②它是
负数.这个数是 .
－3　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. 在数轴上表示下列各数：
①｜－1 ｜；②｜0｜；③绝对值是1.5的负数；
④绝对值是3 的有理数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】① ＝1 ；②｜0｜＝0；③绝对值是1.5的负
数是－1.5；④绝对值是3 的有理数是±3 ，在数轴上表
示各数如答图所示：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
与绝对值有关的计算
9. 已知a＝－2，b＝1，则｜a｜＋｜－b｜的值为(　A　)
A. 3 B. 1 C. 0 D. －1
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. [母题 教材P22作业题T2]计算：
(1)｜－7｜＋ － ；
【解】原式＝7＋ －
＝7 .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2) － .
【解】原式＝ －
＝ .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. [新考法·分类讨论法]若a＝－5，｜a｜＝｜b｜，则b
的值等于(　D　)
A. ＋5 B. －5
C. 0 D. ±5
D
[易错题]因忽略绝对值相等的两个数有两种情况而漏解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
③如果｜a｜＝｜b｜，那么a＝±b；
④如果a是负数，那么a＋1是正数.
其中正确的个数是(　A　)
A. 1个 B. 2个
C. 3个 D. 4个
A
12. [2024·遂宁期中]下列说法：
①如果｜a｜＝－a，那么a为负数；
②如果a2＝b2，那么a＝b；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13. 若｜a－5｜＋｜b－2｜＝0，则a＋b＝ .
14. 如图，在数轴上，点B在点A的右侧.已知点A对应的数
为－1，点B对应的数为m，点C到原点的距离为2，且
AC＋BC＝5，则m的值为 .
7　
0或2或4　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
因为点C到原点的距离为2，
所以点C对应的数为±2.
当点C对应的数为2时，因为点A对应的数为－1，
所以AC＝3.
因为AC＋BC＝5，所以BC＝2，
所以点B对应的数为0或4，即m＝0或m＝4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
当m＝0或m＝4时，点B都在点A的右侧，符合题
意.
当点C对应的数为－2时，AC＝1，
因为AC＋BC＝5，所以BC＝4，
所以点B对应的数为2或－6，即m＝2或m＝－6.
当m＝2时，点B在点A的右侧，符合题意；当m
＝－6时，点B在点A的左侧，不符合题意.
综上可知，m的值为0或2或4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. [情境题·生活应用]某出租车司机一日从公司出发，在东
西方向的人民路上连续接送5批客人，行驶路程记录如下
(规定向东为正，向西为负，单位：km)：
第1批 第2批 第3批 第4批 第5批
5 2 －4 －3 10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
若该出租车每千米耗油0.08升，那么在这个过程中共耗
油多少升？
【解】｜5｜＋｜2｜＋｜－4｜＋｜－3｜＋｜10｜＝
24(km)，
0.08×24＝1.92(升).
答：在这个过程中共耗油1.92升.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16. [新考法·阅读类比法]同学们都知道，｜7－(－1)｜表示7
与－1之差的绝对值，实际上也可以理解为7与－1两数在
数轴上所对应的两点之间的距离.如｜x－6｜的几何意
义是数轴上表示数x的点与表示数6的点之间的距离.试
探索：
(1)求｜3－(－2)｜＝ ；若｜x－(－2)｜＝3，则x
＝ ；
(2)｜x－1｜＋｜x－(－3)｜的最小值是 ；
(3)求当x为何值时，｜x－(－1)｜＋｜x－2｜＋｜x－
4｜的值最小，最小值多少？
5　
1或－5　
4　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】因为｜x－(－1)｜＋｜x－2｜＋｜x－4｜可
以理解为表示x的点到表示－1，2，4三点的距离
之和，
当－1≤x≤4时， ＋ 有最小值，
最小值为4＋1＝5，
当x＝2时， 有最小值为0，
所以当x＝2时，｜x－(－1)｜＋｜x－2｜＋｜x－
4｜有最小值，最小值为5＋0＝5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看！