1.2 数轴 课件（共39张PPT）

(共39张PPT)
1.2 数轴
第1章 有理数
【2025-2026学年】浙教版 数学 七年级上册
授课教师：********
班 级：********
时 间：********
数轴
课程目标
理解数轴的概念，明确数轴的三要素。
能够正确地画出数轴，并在数轴上表示出有理数。
学会利用数轴比较有理数的大小。
数轴的定义
数轴是一条规定了原点、正方向和单位长度的直线。它是数学中表示数的重要工具，能将抽象的数直观地展示在直线上。
数轴的三要素
原点：在数轴上，确定的一个点表示数 0，这个点就是原点。它是数轴的基准点，所有数的位置都是相对于原点而言的。
正方向：通常规定数轴向右的方向为正方向，用箭头表示。相反，向左的方向则为负方向。
单位长度：数轴上选取适当的长度作为单位长度，用于衡量数轴上点与点之间的距离。例如，可规定 1 厘米代表 1 个单位长度，那么从原点向右 1 厘米的点表示 1，向左 1 厘米的点表示 - 1 。
数轴的绘制步骤
画一条水平的直线。
在直线上选取一点作为原点，用 0 表示。
确定正方向，通常向右为正，画上箭头。
根据实际需要，选取合适的单位长度，并在直线上标出对应的刻度。
数轴上的点与有理数的对应关系
每一个有理数都可以用数轴上的一个点来表示。例如，3 可以用原点右边距离原点 3 个单位长度的点表示；-2 可以用原点左边距离原点 2 个单位长度的点表示；\(\frac{1}{2}\)可以用原点右边距离原点\(\frac{1}{2}\)个单位长度的点表示 。
数轴上的点并不都表示有理数，还可以表示无理数，但我们目前主要研究数轴上表示有理数的点。
利用数轴比较有理数的大小
在数轴上，右边的数总比左边的数大。
正数都大于 0，负数都小于 0，正数大于一切负数。
例如，在数轴上，5 在 3 的右边，所以 5＞3；-1 在 0 的左边，所以 - 1＜0；3 在 - 2 的右边，所以 3＞-2 。
数轴的应用
直观表示数：能清晰地看出数的大小关系和位置分布，如在数轴上可以很容易比较出 - 3、2、0 的大小。
解决实际问题：在行程问题中，可利用数轴表示物体的运动方向和距离。比如，一辆汽车从原点出发，向东行驶 5 千米到达 A 点，向西行驶 3 千米到达 B 点，在数轴上就能直观地表示出 A、B 两点的位置 。
课堂练习
画出一条数轴，并在数轴上表示出 - 4、2.5、0、\(\frac{3}{2}\) 这些数。
利用数轴比较 - 3、1、-5、4 的大小，并用 “＜” 连接起来。
总结
数轴的三要素是原点、正方向和单位长度，这三者缺一不可。
有理数与数轴上的点存在对应关系，每个有理数都能在数轴上找到对应的点。
借助数轴可以方便地比较有理数的大小，右边的数总比左边的数大。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.数轴的概念：规定了原点、单位长度和正方向的直线叫作数轴。
2.数轴的三要素：数轴是一条可以向两个方向无限延伸的直线，
其中原点、单位长度和正方向称为数轴的三要素。在同一数轴中，
数轴的三要素一经确定，就不得改变。（（1）数轴是一条直线，
可以向两方无限延伸，但直线不一定是数轴；（2）同一条数轴
上的单位长度必须一致）
3.数轴的画法：
步骤 画法 图形
一画 画一条直线（一般画成水平的）。 ____________________________________
二取 ______________________________________
三定 规定直线的一个方向（一般取从左到 右的方向）为正方向，用箭头表示， 相反的方向为负方向。 _____________________________________
步骤 画法 图形
四标 __________________________________________
典例1 下列各选项中能正确表示数轴的是( )
D
A. B.
C. D.
解析：A中缺少原点,B中没有标出正方向,C中的单位长度不统一,
故选项A，B，C均不正确;选项D满足数轴的三要素，正确。
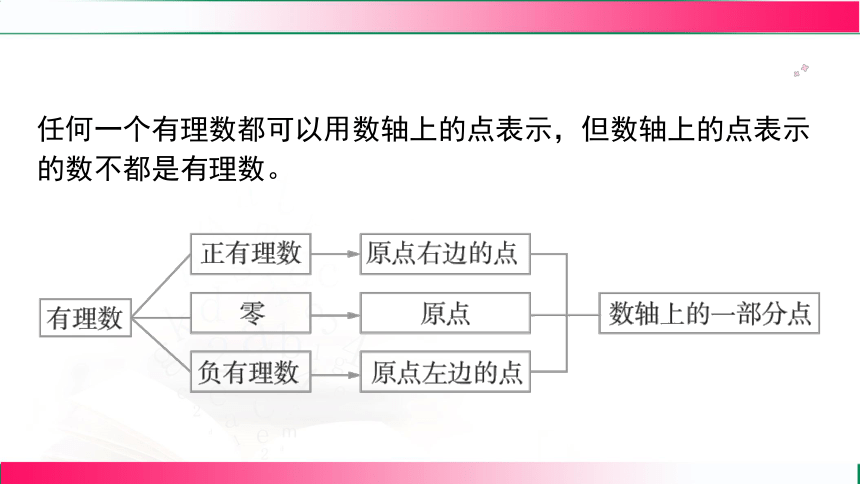
任何一个有理数都可以用数轴上的点表示，但数轴上的点表示
的数不都是有理数。
典例2 （1）如图，数轴上点，，，， 分别表示
什么数？（知点读数）
解：由图可知，点表示，点表示,点表示,
点 表示4,点 表示0。
（2）画出一条数轴，并在数轴上描出表示下列各数的点：
1.5，，，2， 。（ 知数画点）
解：如图所示：
1.相反数：如果两个数只有符号不同,那么我们称其中一个数为
另一个数的相反数,也称这两个数互为相反数（相反数是成对出
现的（0除外））。注意，0的相反数是0。（相反数等于它本身
的数只有0）
2.相反数的几何意义
在数轴上，表示互为相反数（0除外）的两个点，位于原点的
两侧，并且到原点的距离相等。
任何一个数都有唯一的相反数。
典例3 求下列各数的相反数。
，，，0，， 。
解：它们的相反数依次是，2，，0，6， 。
求一个数的相反数的方法
（1）若该数为正数，则直接在前面加“-”，若该数为负数，则
直接去掉符号，0的相反数仍是0；
（2）求一个字母或一个式子的相反数时，只需在这个字母或
这个式子的前面加上“-”，如的相反数为,的相反数为
。（ 可以是正数、零、负数）
解题通法
知识过关
①数轴的三要素： 　原点　、 　单位长度　、 　正方向　.
②任何一个有理数都可以用 　数轴上的点　表示.
③如果两个数只有 　符号　不同，那么我们称其中一个数为另
一个数的相反数；0的相反数是 　0　.
④在数轴上，表示互为相反数(0除外)的两个点，位于 　原点　
的两侧，并且到 　原点　的距离相等.
原点
单位长度
正方向
数轴上的点
符号
0
原点
原点
数轴的概念及画法
1. 下列关于数轴的画法不正确的有(　B　)
A. 4个 B. 3个
C. 2个 D. 1个
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. 下列语句中，错误的是(　B　)
A. 数轴上原点位置的确定是任意的
B. 数轴上两个不同的点可以表示同一个有理数
C. 数轴上单位长度的确定，可根据需要任意选取
D. 数轴上表示原点的数是0
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
数轴上的点与有理数的关系
3. 如图，数轴上玩偶所在点表示的数可能为(　C　)
A. 3 B. 1
C. －1 D. －4
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. 画出数轴，用数轴上的点表示下列各数.
3，－2，1.5，－ ，0，－0.5.
【解】如答图所示：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
相反数
5. 2 024的相反数是(　B　)
A. 2 024 B. －2 024
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6. [2024·长沙雨花区二模]有理数a，b，c在数轴上的对应
点的位置如图所示.若有理数a，b互为相反数，则下列
结论正确的是(　D　)
A. c＝0 B. b＜0
C. c＞0 D. c＜0
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 如图，数轴上A，B两点表示的数互为相反数，且点A与
点B之间的距离为4个单位长度，则点A表示的数是
.
－2　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. 已知a是－1的相反数，b的相反数是－3，c是最小的自
然数，求a＋b＋c的值.
【解】由题意，知a＝1，b＝3，c＝0，
所以a＋b＋c＝4.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[易错题]在数轴上根据距离求点时漏解
9. [母题 教材P20作业题T6]数轴上点A表示－3，从点A出
发，沿数轴移动4个单位长度到达点B，则点B表示的数
是 .
1或－7　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. [2024·苏州高新区期末]将一把刻度尺按如图所示的方式
放在数轴上(数轴的单位长度是1 cm)，刻度尺上的“1”
和“6”分别对应数轴上“－1.2”和“x”，则x的值
为(　A　)
A. 3.8 B. 2.8
C. 4.8 D. 6
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. 如图，在数轴上，注明了四段的范围，若某段上有两个
整数，则这段是(　A　)
A. 段① B. 段②
C. 段③ D. 段④
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. [新趋势·跨学科]5个城市的国际标准时间(单位：时)在数
轴上表示如图所示，那么北京时间2024年12月1日20时应
是(　B　)
A. 纽约时间2024年12月1日5时
B. 巴黎时间2024年12月1日13时
C. 首尔时间2024年12月1日19时
D. 伦敦时间2024年12月1日11时
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13. 如图，数轴上有A，B，C三点，A，B两点表示的有
理数分别是－2和8，若将该数轴从点C处折叠后，点A
和点B恰好重合，那么点C表示的有理数是 .
3　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. [2024·商洛期末]如图，数轴上标出了7个点，相邻两点之
间的距离都相等，已知点A表示－4，点G表示8.
(1)点B表示的有理数是 ，原点是点 .
(2)图中哪些点表示的有理数互为相反数？
【解】B和D，A和E.
－2　
C　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)图中的数轴上另有点M，到点A，点G的距离之和为
13，求点M表示的有理数.
【解】AG＝8＋4＝12，如果点M在点A，G之间，则AM＋MG＝AG＝12，与题意不符，故点M不在点A，G之间.当点M在点A的左侧时，MA＋MG＝MA＋MA＋AG＝13，得MA＝0.5，所以点M表示－4.5；当点M在点G的右侧时，MA＋MG＝MG＋MG＋AG＝13，得MG＝0.5，所以点M表示8.5.综上，点M表示－4.5或8.5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. [情境题·生活应用]一辆货车从百货大楼出发负责送货，
向东走了4千米到达小明家，继续向东走了1.5千米到达
小红家，然后向西走了8.5千米到达小刚家，最后返回百
货大楼.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)如图，以百货大楼为原点，向东为正方向，1个单位
长度表示1千米，请你在数轴上标出小明家、小红
家、小刚家的位置.(小明家用点A表示，小红家用点
B表示，小刚家用点C表示)
【解】如图所示：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)小明家与小刚家相距多远？
【解】小明家到百货大楼是4千米，小刚家到百货大
楼是3千米，所以小明家与小刚家相距4＋3＝7(千米).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)若货车每千米耗油0.1升，那么这辆货车此次送货共
耗油多少升？
【解】这辆货车此次送货共耗油：(4＋1.5＋8.5＋
3)×0.1＝1.7(升).
答：这辆货车此次送货共耗油1.7升.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16. [新考法·折叠法]已知在纸面上有一数轴如图所示，折叠
纸面.
(1)若数轴上表示1的点与表示－1的点重合，则表示－2
的点与表示何数的点重合？
【解】表示－2的点与表示2的点重合；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若数轴上表示－1的点与表示5的点重合，则表示0的
点与表示何数的点重合？
【解】表示0的点与表示4的点重合；
(3)若将数轴上表示－1的点与表示5的点之间的线段对折
2次，展开后，请写出所有折点表示的数.
【解】所有折点表示的数分别为0.5，2，3.5.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看！