2.1 有理数的加法 课件(共33张PPT)
文档属性
| 名称 | 2.1 有理数的加法 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览











文档简介
(共33张PPT)
2.1 有理数的加法
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的加法
课程目标
理解有理数加法的意义,掌握有理数加法的法则。
能够熟练运用有理数加法法则进行计算。
了解有理数加法的运算律,并能运用运算律简化计算。
学会运用有理数加法解决实际问题。
有理数加法的定义
有理数的加法是指求两个或多个有理数的和的运算。与小学阶段学习的正数加法不同,有理数加法还涉及负数的相加。
有理数加法法则
同号两数相加:取相同的符号,并把绝对值相加。
例如:(+3)+(+5)= +(3+5)= +8;(-3)+(-5)= -(3+5)= -8 。
异号两数相加
绝对值相等时(互为相反数的两数相加),和为 0。例如:(+3)+(-3)= 0 。
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。例如:(+5)+(-3)= +(5-3)= +2;(-5)+(+3)= -(5-3)= -2 。
一个数与 0 相加:仍得这个数。例如:0 +(+5)= +5;0 +(-5)= -5 。
有理数加法的运算步骤
确定和的符号:根据两个加数的符号,按照加法法则确定和的符号。
计算和的绝对值:依据加法法则计算和的绝对值。
写出结果:将确定的符号和计算出的绝对值组合起来,得到加法的结果。
有理数加法的运算律
加法交换律:两个数相加,交换加数的位置,和不变。用字母表示为:a + b = b + a 。例如:(+3)+(-5)=(-5)+(+3)= -2 。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。用字母表示为:(a + b)+ c = a +(b + c)。例如:[(+3)+(-5)] +(+2)=(+3)+[(-5)+(+2)] = 0 。
运用运算律简化计算
在进行多个有理数相加时,合理运用加法交换律和结合律,可以使计算更加简便。
例如:计算(-2)+(+3)+(+4)+(-5)
运用交换律和结合律可得:[(-2)+(-5)] + [(+3)+(+4)] =(-7)+(+7)= 0 。
实际应用举例
一个物体作左右方向的运动,规定向右为正,向左为负。如果物体先向右运动 5 米,再向右运动 3 米,那么两次运动的最后结果是什么?
可列式为:(+5)+(+3)= +8(米),即物体向右运动了 8 米。
小明的银行卡里原有 100 元,第一天存入 50 元,第二天取出 30 元,这时银行卡里有多少钱?
列式为:100 +(+50)+(-30)= 100 + 50 - 30 = 120(元),即银行卡里有 120 元。
课堂练习
计算下列各题:
(+7)+(+8)
(-7)+(-8)
(+7)+(-8)
(-7)+(+8)
0 +(-9)
运用运算律计算:(-12)+(+11)+(-8)+(+39)
总结
有理数加法法则是进行有理数加法运算的依据,要根据加数的符号情况正确应用法则。
计算时要先确定符号,再计算绝对值。
加法交换律和结合律可以简化有理数加法的计算,在实际运算中要灵活运用。
有理数加法在生活中有着广泛的应用,能帮助我们解决一些实际的数量变化问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.通过借助数轴理解有理数加法的意义,体会数形结合的
思想方法。
2.掌握有理数的加法法则,能熟练进行有理数的加法运算。
3.理解有理数加法的交换律和结合律,能运用加法运算律
简化运算,提高运算能力。
4.能运用有理数的加法解决简单的实际问题,形成应用意识。
1.有理数加法法则
类型 加法法则 示例
同号 相加 同号两数相加,取与加 数相同的符号,并把绝 对值相加。 __________________________________________
类型 加法法则 示例
异号 相加 异号两数相加,取绝对 值较大的加数的符号, 并用较大的绝对值减去 较小的绝对值。 __________________________________________________
互为相反数的两个数 相加得0。
类型 加法法则 示例
同0相加 一个数同0相加,仍 得这个数。 ____________________________________________________
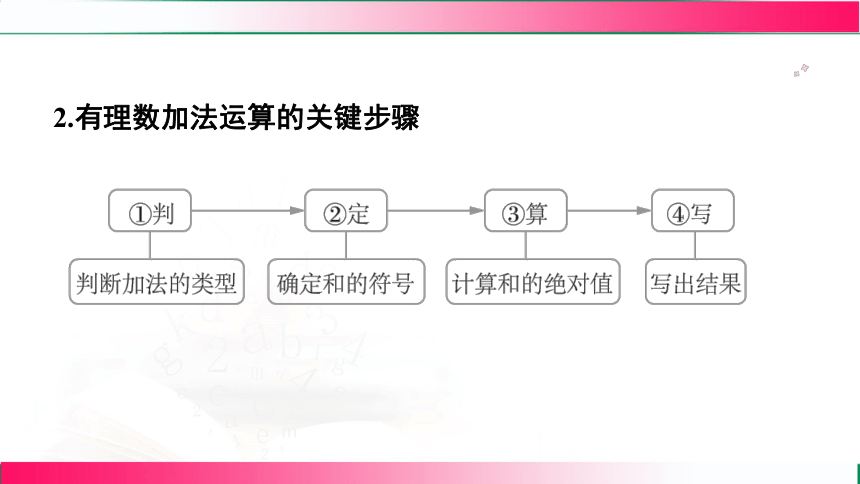
2.有理数加法运算的关键步骤
典例1 计算:
(1) ;
解: 。
一个数加一个正数,所得的和大于这个数,一个数加一个负数,所得的和小于这个数。
(2) ;
解: 。
一个数加一个正数,所得的和大于这个数,一个数加
一个负数,所得的和小于这个数。
(3) ;
解: 。
(4) 。
解: 。
互为相反数的两个数的和为0,反之也成立。
任何数同0相加,仍得这个数。
运算律 文字叙述 式子表示
加法交 换律 两个数相加,交换加数的位置,和不变。
加法结 合律 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
易错:
利用有理数的加法交换律时,要连同加数的符号一起交换,必要时需加括号,如。
有理数的加法运算律不但适用于两个数或三个数相加,
而且适用于三个以上的有理数相加。
知识过关
①法则:同号两数相加,取 与加数相同 的符号,并把 绝
对值 相加.异号两数相加,取 绝对值较大的加数 的符
号,并用 较大的绝对值 减去 较小的绝对值 .互为相
反数的两个数相加得 0 ;一个数同0相加,仍得 这个
数 .
②计算步骤:先确定结果的符号,再确定结果的绝对值.
与加数相同
绝
对值
绝对值较大的加数
较大的绝对值
较小的绝对值
0
这个
数
有理数的加法法则
1. 下列计算结果错误的是( D )
A. (-5)+(-3)=-8
B. (-5)+(+3)=-2
C. (-5)+(+5)=0
D. (-3)+0=0
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2. [2023·温州]如图,比数轴上点A表示的数大3的数是
( D )
A. -1 B. 0 C. 1 D. 2
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. 对于有理数a,b有下列说法:
①若a+b=0,则a与b互为相反数;
②若a+b<0,则a与b异号;
③若a+b>0,且a与b同号,则a>0,b>0;
④若|a|>|b|,且a,b异号,则a+b>0.
其中,正确的说法有 .(填写序号)
①③
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4. [母题 教材P34例1]计算:
(1)(+14)+(+6);
(2)(+16)+(-5);
【解】(+14)+(+6)
=+(14+6)
=+20.
【解】(+16)+(-5)
=+(16-5)
=+11.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)(-0.75)+ ;
(4)0+ .
【解】(-0.75)+
=0.
【解】0+
=-1 .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
有理数加法的应用
5. m是有理数,则m+|m|( B )
A. 可能是负数
B. 不可能是负数
C. 一定是正数
D. 可能是正数,也可能是负数
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. [新考向·数学文化]中国人最先使用负数,魏晋时期的数学
家刘徽在“正负术”的注文中指出,可将算筹(小棍形状
的记数工具)正放表示正数,斜放表示负数.如图,根据刘
徽的这种表示法,图①可列式计算为(+1)+(-1)=0,由
此可推算图②中计算所得的结果为( C )
A. +1 B. +7
C. -1 D. -7
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. 在计算|(-5)+□|的□中填上一个数,使结果等于
11,这个数是( D )
A. 16 B. 6
C. 16或6 D. 16或-6
8. 绝对值大于1且不大于4的所有整数的和是( C )
A. 8 B. -8 C. 0 D. 4
D
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. [2023·宁波舜水中学期中]两数相加,其和小于每一个加
数,那么( B )
A. 这两个加数一定有一个为零
B. 这两个加数一定都是负数
C. 这两个加数一正一负且负数的绝对值大
D. 这两个加数的符号无法确定
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10. [新视角·新定义题]定义新运算:对任意有理数a,b都
有a b= + ,例如,2 3= + = ,那么4
(-3)的值是 .
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
示例:如图①,4+3=7.
如图②,当x=2,y=- 时,z= .
11. 约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12. [新视角·开放性试题]小毛同学的作业本上出现了一个错
误的等式-3+2=5,请你在算式中添“括号”或“绝对
值符号”或“负号”(不限定个数),使等式成立,添加
符号后的等式为 .
+2=5(答案不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(1)[3.6]+[-2.7];
【解】[3.6]+[-2.7]=3+(-3)=0.
(2)[6.25]+[-3].
【解】[6.25]+[-3]=6+(-3)=3.
13. 若规定用[x]表示不超过x的整数中的最大的整数,如
[2.34]=2,[-3.24]=-4,计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. [新视角·规律探究题]如图,从左边第一个圆圈开始向右
数,在每个圆圈中都填入一个整数,使得其中任意三个
相邻圆圈中所填整数之和都相等.
(1)可求得a= ,b= ;
(2)第2 024个圆圈中的数为 ;
-6
2
-6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)若前m个圆圈中所填整数之和为2 015,求m的值.
【解】由题易知圆圈中的数的规律是9,-6,2的
循环.因为9+(-6)+2=5,所以每一个循环组的和为5.因为2 015÷5=403,所以2 015是403个循环组的和.因为403×3=1 209,所以m的值为1 209.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. 若|a|=14,|b|=2 024,|a+b|≠a+b,试
计算a+b的值.
【解】因为|a|=14,所以a=±14.
因为|b|=2 024,所以b=±2 024.
因为|a+b|≠a+b,
所以a+b<0.
当a=14,b=-2 024时,a+b=14+(-2 024)=
-2 010;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
当a=-14,b=-2 024时,a+b=(-14)+(-2 024)
=-2 038;
当b=2 024时,不合题意.
综上,a+b的值为-2 010或-2 038.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
谢谢观看!
2.1 有理数的加法
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的加法
课程目标
理解有理数加法的意义,掌握有理数加法的法则。
能够熟练运用有理数加法法则进行计算。
了解有理数加法的运算律,并能运用运算律简化计算。
学会运用有理数加法解决实际问题。
有理数加法的定义
有理数的加法是指求两个或多个有理数的和的运算。与小学阶段学习的正数加法不同,有理数加法还涉及负数的相加。
有理数加法法则
同号两数相加:取相同的符号,并把绝对值相加。
例如:(+3)+(+5)= +(3+5)= +8;(-3)+(-5)= -(3+5)= -8 。
异号两数相加
绝对值相等时(互为相反数的两数相加),和为 0。例如:(+3)+(-3)= 0 。
绝对值不相等时,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值。例如:(+5)+(-3)= +(5-3)= +2;(-5)+(+3)= -(5-3)= -2 。
一个数与 0 相加:仍得这个数。例如:0 +(+5)= +5;0 +(-5)= -5 。
有理数加法的运算步骤
确定和的符号:根据两个加数的符号,按照加法法则确定和的符号。
计算和的绝对值:依据加法法则计算和的绝对值。
写出结果:将确定的符号和计算出的绝对值组合起来,得到加法的结果。
有理数加法的运算律
加法交换律:两个数相加,交换加数的位置,和不变。用字母表示为:a + b = b + a 。例如:(+3)+(-5)=(-5)+(+3)= -2 。
加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。用字母表示为:(a + b)+ c = a +(b + c)。例如:[(+3)+(-5)] +(+2)=(+3)+[(-5)+(+2)] = 0 。
运用运算律简化计算
在进行多个有理数相加时,合理运用加法交换律和结合律,可以使计算更加简便。
例如:计算(-2)+(+3)+(+4)+(-5)
运用交换律和结合律可得:[(-2)+(-5)] + [(+3)+(+4)] =(-7)+(+7)= 0 。
实际应用举例
一个物体作左右方向的运动,规定向右为正,向左为负。如果物体先向右运动 5 米,再向右运动 3 米,那么两次运动的最后结果是什么?
可列式为:(+5)+(+3)= +8(米),即物体向右运动了 8 米。
小明的银行卡里原有 100 元,第一天存入 50 元,第二天取出 30 元,这时银行卡里有多少钱?
列式为:100 +(+50)+(-30)= 100 + 50 - 30 = 120(元),即银行卡里有 120 元。
课堂练习
计算下列各题:
(+7)+(+8)
(-7)+(-8)
(+7)+(-8)
(-7)+(+8)
0 +(-9)
运用运算律计算:(-12)+(+11)+(-8)+(+39)
总结
有理数加法法则是进行有理数加法运算的依据,要根据加数的符号情况正确应用法则。
计算时要先确定符号,再计算绝对值。
加法交换律和结合律可以简化有理数加法的计算,在实际运算中要灵活运用。
有理数加法在生活中有着广泛的应用,能帮助我们解决一些实际的数量变化问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.通过借助数轴理解有理数加法的意义,体会数形结合的
思想方法。
2.掌握有理数的加法法则,能熟练进行有理数的加法运算。
3.理解有理数加法的交换律和结合律,能运用加法运算律
简化运算,提高运算能力。
4.能运用有理数的加法解决简单的实际问题,形成应用意识。
1.有理数加法法则
类型 加法法则 示例
同号 相加 同号两数相加,取与加 数相同的符号,并把绝 对值相加。 __________________________________________
类型 加法法则 示例
异号 相加 异号两数相加,取绝对 值较大的加数的符号, 并用较大的绝对值减去 较小的绝对值。 __________________________________________________
互为相反数的两个数 相加得0。
类型 加法法则 示例
同0相加 一个数同0相加,仍 得这个数。 ____________________________________________________
2.有理数加法运算的关键步骤
典例1 计算:
(1) ;
解: 。
一个数加一个正数,所得的和大于这个数,一个数加一个负数,所得的和小于这个数。
(2) ;
解: 。
一个数加一个正数,所得的和大于这个数,一个数加
一个负数,所得的和小于这个数。
(3) ;
解: 。
(4) 。
解: 。
互为相反数的两个数的和为0,反之也成立。
任何数同0相加,仍得这个数。
运算律 文字叙述 式子表示
加法交 换律 两个数相加,交换加数的位置,和不变。
加法结 合律 三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
易错:
利用有理数的加法交换律时,要连同加数的符号一起交换,必要时需加括号,如。
有理数的加法运算律不但适用于两个数或三个数相加,
而且适用于三个以上的有理数相加。
知识过关
①法则:同号两数相加,取 与加数相同 的符号,并把 绝
对值 相加.异号两数相加,取 绝对值较大的加数 的符
号,并用 较大的绝对值 减去 较小的绝对值 .互为相
反数的两个数相加得 0 ;一个数同0相加,仍得 这个
数 .
②计算步骤:先确定结果的符号,再确定结果的绝对值.
与加数相同
绝
对值
绝对值较大的加数
较大的绝对值
较小的绝对值
0
这个
数
有理数的加法法则
1. 下列计算结果错误的是( D )
A. (-5)+(-3)=-8
B. (-5)+(+3)=-2
C. (-5)+(+5)=0
D. (-3)+0=0
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2. [2023·温州]如图,比数轴上点A表示的数大3的数是
( D )
A. -1 B. 0 C. 1 D. 2
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. 对于有理数a,b有下列说法:
①若a+b=0,则a与b互为相反数;
②若a+b<0,则a与b异号;
③若a+b>0,且a与b同号,则a>0,b>0;
④若|a|>|b|,且a,b异号,则a+b>0.
其中,正确的说法有 .(填写序号)
①③
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
4. [母题 教材P34例1]计算:
(1)(+14)+(+6);
(2)(+16)+(-5);
【解】(+14)+(+6)
=+(14+6)
=+20.
【解】(+16)+(-5)
=+(16-5)
=+11.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)(-0.75)+ ;
(4)0+ .
【解】(-0.75)+
=0.
【解】0+
=-1 .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
有理数加法的应用
5. m是有理数,则m+|m|( B )
A. 可能是负数
B. 不可能是负数
C. 一定是正数
D. 可能是正数,也可能是负数
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
6. [新考向·数学文化]中国人最先使用负数,魏晋时期的数学
家刘徽在“正负术”的注文中指出,可将算筹(小棍形状
的记数工具)正放表示正数,斜放表示负数.如图,根据刘
徽的这种表示法,图①可列式计算为(+1)+(-1)=0,由
此可推算图②中计算所得的结果为( C )
A. +1 B. +7
C. -1 D. -7
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. 在计算|(-5)+□|的□中填上一个数,使结果等于
11,这个数是( D )
A. 16 B. 6
C. 16或6 D. 16或-6
8. 绝对值大于1且不大于4的所有整数的和是( C )
A. 8 B. -8 C. 0 D. 4
D
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. [2023·宁波舜水中学期中]两数相加,其和小于每一个加
数,那么( B )
A. 这两个加数一定有一个为零
B. 这两个加数一定都是负数
C. 这两个加数一正一负且负数的绝对值大
D. 这两个加数的符号无法确定
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10. [新视角·新定义题]定义新运算:对任意有理数a,b都
有a b= + ,例如,2 3= + = ,那么4
(-3)的值是 .
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
示例:如图①,4+3=7.
如图②,当x=2,y=- 时,z= .
11. 约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
12. [新视角·开放性试题]小毛同学的作业本上出现了一个错
误的等式-3+2=5,请你在算式中添“括号”或“绝对
值符号”或“负号”(不限定个数),使等式成立,添加
符号后的等式为 .
+2=5(答案不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(1)[3.6]+[-2.7];
【解】[3.6]+[-2.7]=3+(-3)=0.
(2)[6.25]+[-3].
【解】[6.25]+[-3]=6+(-3)=3.
13. 若规定用[x]表示不超过x的整数中的最大的整数,如
[2.34]=2,[-3.24]=-4,计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. [新视角·规律探究题]如图,从左边第一个圆圈开始向右
数,在每个圆圈中都填入一个整数,使得其中任意三个
相邻圆圈中所填整数之和都相等.
(1)可求得a= ,b= ;
(2)第2 024个圆圈中的数为 ;
-6
2
-6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)若前m个圆圈中所填整数之和为2 015,求m的值.
【解】由题易知圆圈中的数的规律是9,-6,2的
循环.因为9+(-6)+2=5,所以每一个循环组的和为5.因为2 015÷5=403,所以2 015是403个循环组的和.因为403×3=1 209,所以m的值为1 209.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. 若|a|=14,|b|=2 024,|a+b|≠a+b,试
计算a+b的值.
【解】因为|a|=14,所以a=±14.
因为|b|=2 024,所以b=±2 024.
因为|a+b|≠a+b,
所以a+b<0.
当a=14,b=-2 024时,a+b=14+(-2 024)=
-2 010;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
当a=-14,b=-2 024时,a+b=(-14)+(-2 024)
=-2 038;
当b=2 024时,不合题意.
综上,a+b的值为-2 010或-2 038.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
