2.2 有理数的减法 课件(共36张PPT)
文档属性
| 名称 | 2.2 有理数的减法 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览







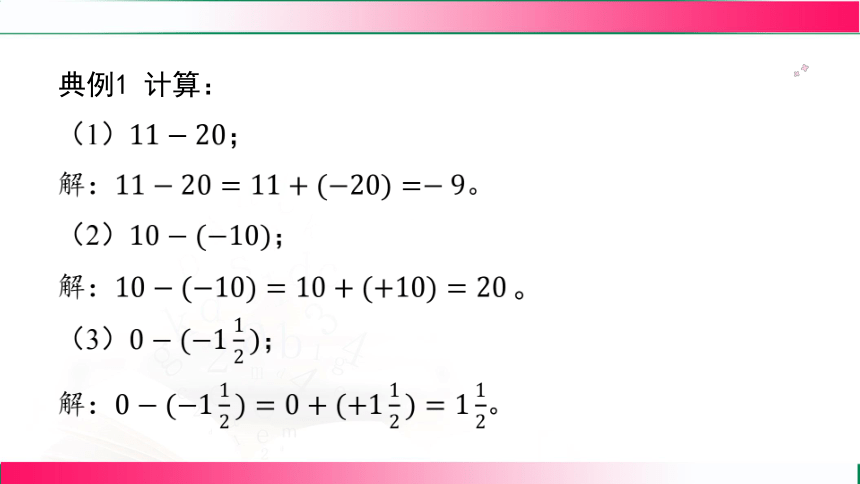




文档简介
(共36张PPT)
2.2 有理数的减法
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的减法
课程目标
深刻理解有理数减法的意义,熟练掌握有理数减法法则。
能够准确无误地运用有理数减法法则进行各类计算。
学会灵活运用运算技巧,简化有理数减法运算过程。
能够运用有理数减法知识,有效解决实际生活中的数学问题。
有理数减法的定义
有理数减法是已知两个有理数加数的和与其中一个加数,求另一个加数的运算,它是加法的逆运算。例如,已知\(a + b = c\),那么\(c - b = a\),这里\(c - b\)就是有理数减法运算。
有理数减法法则
减去一个数,等于加上这个数的相反数。用式子表示为:\(a - b = a + (-b)\) 。这其中有 “两变一不变”:
两变:
运算符号改变,减法运算变为加法运算。
减数改变,减数变成它的相反数。
一不变:被减数保持不变。
有理数减法运算步骤
将减法运算转化为加法运算,即把减号变为加号,同时将减数变为它的相反数。
按照有理数加法法则进行计算。先确定和的符号,再计算和的绝对值。
实例演示
计算\(5 - 3\):
依据法则,转化为加法:\(5 - 3 = 5 + (-3)\) 。
按照加法法则计算:因为\(5\)是正数,\(-3\)是负数,异号两数相加,\(5\)的绝对值大于\(-3\)的绝对值,所以取\(5\)的符号为正号,并用\(5\)的绝对值减去\(-3\)的绝对值,即\(5 - 3 = 5 + (-3) = +(5 - 3) = 2\) 。
计算\(3 - 5\):
转化为加法:\(3 - 5 = 3 + (-5)\) 。
按加法法则计算:\(3\)是正数,\(-5\)是负数,异号两数相加,\(-5\)的绝对值大于\(3\)的绝对值,所以取\(-5\)的符号为负号,并用\(-5\)的绝对值减去\(3\)的绝对值,即\(3 - 5 = 3 + (-5) = -(5 - 3) = -2\) 。
有理数减法运算技巧
凑整法:若被减数和减数接近某个整数,可将减数凑整,简化计算。例如计算\(45 - 29.5\),可将\(29.5\)看作\(30\),先算\(45 - 30 = 15\),因为多减了\(0.5\),所以结果要加上\(0.5\),即\(45 - 29.5 = 15 + 0.5 = 15.5\) 。
运用运算律:在多个有理数加减混合运算中,可利用加法交换律和结合律调整数的顺序或组合。例如计算\(15 + 23 - 10 - 13\),可利用交换律和结合律变形为\((15 - 10) + (23 - 13) = 5 + 10 = 15\) 。
分数运算技巧:进行分数减法运算时,若分母不同,需先通分,化为同分母分数再相减。例如计算\(\frac{3}{4} - \frac{1}{3}\),先通分,\(4\)和\(3\)的最小公倍数是\(12\),则\(\frac{3}{4} - \frac{1}{3} = \frac{3 3}{4 3} - \frac{1 4}{3 4} = \frac{9}{12} - \frac{4}{12} = \frac{9 - 4}{12} = \frac{5}{12}\) 。
实际应用举例
温度问题:某天最高气温是\(8 \),最低气温是\(-3 \),这天的温差是多少?
温差 = 最高气温 - 最低气温,即\(8 - (-3)\) 。
根据减法法则,转化为加法:\(8 - (-3) = 8 + 3 = 11( )\) ,所以这天的温差是\(11 \) 。
海拔问题:A 地海拔高度为\(200\)米,B 地海拔高度为\(-50\)米,A 地比 B 地高多少米?
可列式为\(200 - (-50)\) 。
转化为加法:\(200 - (-50) = 200 + 50 = 250\)(米),即 A 地比 B 地高\(250\)米。
经济问题:某商店上周盈利\(300\)元,本周盈利\(-50\)元,上周比本周多盈利多少元?
多盈利的金额 = 上周盈利 - 本周盈利,即\(300 - (-50)\) 。
转化为加法计算:\(300 - (-50) = 300 + 50 = 350\)(元),所以上周比本周多盈利\(350\)元。
课堂练习
计算下列各题:
\(7 - 4\)
\((-7) - 4\)
\(7 - (-4)\)
\((-7) - (-4)\)
\(0 - 5\)
\(5 - 0\)
运用运算技巧计算:
\(35 - 19.8\)
\(12 + 25 - 18 - 12\)
\(\frac{5}{6} - \frac{1}{4}\)
解决实际问题:
潜水员在水下\(30\)米处,记作\(-30\)米,上升\(15\)米后,他现在的位置是多少米?
总结
有理数减法法则是 “减去一个数,等于加上这个数的相反数”,计算时要遵循 “两变一不变” 原则。
运算时先将减法转化为加法,再按加法法则计算。
灵活运用凑整法、运算律和分数运算技巧等,可以使计算更简便。
有理数减法在温度、海拔、经济等实际生活场景中有广泛应用,要学会将实际问题转化为数学问题并解决。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数的减法法则,能熟练进行有理数的减法运算,提
高运算能力。
2.能把有理数的加减混合运算转化成加法运算,体会转化思想。
3.能将和式中的括号和加号省略,并利用加法运算律进行计算。
4.能运用有理数的加减法解决简单的实际问题,形成应用意识。
1.有理数的减法法则:减去一个数,等于加上这个数的相反数。
用字母表示: 。
2.将减法转化为加法时要注意“两变一不变”:
“两变”是指运算符号“-”需要变成“ ”,减数变成它的
相反数;“一不变”是指被减数不变。
(1)任何数减去0,仍得这个数;0减去一个数,得这个数的相反数。
(2)减法没有交换律,被减数与减数的位置不能改变。
教材延伸 两数相减,差的符号的确定
(1)较大的数-较小的数正数,即若,则 ;反之,若,则 。
(2)较小的数-较大的数负数,即若,则 ;反之,若,则 。
(3)相等的两个数的差为0,即若,则 ;反之,若,则 。
上述结论也常用于“作差法比较两个有理数的大小”。
典例1 计算:
(1) ;
解: 。
(2) ;
解: 。
(3) ;
解: 。
(4) ;
解: 。
(5) ;
解: 。
一个数减一个正数,所得的差小于这个数;
一个数减一个负数,所得的差大于这个数。
(6) 。
解: 。
有理数减法运算“三步曲”
(1)把减号变为加号(改变运算符号);
(2)把减数变为它的相反数(改变性质符号);
(3)按照加法运算的步骤进行运算。
我们可以把算式 中各个加数的括号和括号
前面的加号省略,写成,这个算式仍可看作和式,
读作“正 、负 与正的和”(按式子表示的意义读),或
者读作“减加 ”(按运算的意义读)。这样给算法的选择
和书写带来方便。
典例2 把写成省略“ ”号和
括号的形式,并写出它的读法。
解:
。
读作“负6、正7、负9、正3的和”,或者读作“负6加7减9加3”。
省略的是运算符号,性质符号必须保留。
第1个数前面的符号是性质符号。
有理数加减混合运算的步骤:
(1)遇减化加:利用减法法则,将减法转化为加法;
(2)运用加法交换律和结合律,简化运算;
(3)求出结果。
(1) ;
解:
(把减法转化为加法)
(加法交换律)
(加法结合律)
。
交换加数的位置时,必须连同加数前面的符号一起交换。
典例3 计算:
(2) 。
解:
(将减法转化成加法)
(加法交换律)
(加法结合律)
。
知识过关
减去一个数,等于加上这个数的 相反数 .
相反数
有理数的减法法则
1. [2024·天津]计算3-(-3)的结果是( D )
A. -6 B. 0 C. 3 D. 6
D
1
2
3
4
5
6
7
8
9
10
11
12
13
2. [2024·石家庄期末]下列算式:①2-(-2)=0;②(-3)-
(+3)=0;③(-3)-|-3|=0;④0-(-1)=1.其中正
确的有( A )
A. 1个 B. 2个
C. 3个 D. 4个
A
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 下列说法:
①减去一个负数等于加上这个数的相反数;
②正数减负数,差为正数;
③零减去一个数,仍得这个数;
④两数相减,差一定小于被减数;
⑤两数相减,差不一定小于被减数;
⑥互为相反数的两数相减得零.
其中正确的有( B )
A. 2个 B. 3个
C. 4个 D. 5个
B
1
2
3
4
5
6
7
8
9
10
11
12
13
4. [母题 教材P42作业题T2]计算:
(1)-2-(+10);
(2)0-(-3.6);
【解】-2-(+10)
=-2+(-10)
=-12.
【解】0-(-3.6)
=0+3.6
=3.6.
1
2
3
4
5
6
7
8
9
10
11
12
13
(3)(-30)-(-6);
(4)(+13)-(+16).
【解】(-30)-(-6)
=(-30)+6
=-24.
【解】(+13)-(+16)
=+13+(-16)
=-3.
1
2
3
4
5
6
7
8
9
10
11
12
13
有理数减法法则的应用
5. [新考向·知识情境化]圆圆想了解某地某天的天气情况,在
某气象网站查询到该地这天的最低气温为-6 ℃,最高气
温为2 ℃,则该地这天的温差(最高气温与最低气温的差)
为( D )
A. -8 ℃ B. -4 ℃
C. 4 ℃ D. 8 ℃
D
1
2
3
4
5
6
7
8
9
10
11
12
13
6. [情境题·生活应用]某商店出售三种不同品牌的大米,米袋
上分别标有质量如表.现从中任意拿出两袋不同品牌的大
米,这两袋大米的质量最多相差( A )
大米种类 A品牌大米 B品牌大米 C品牌大米
质量标示 (10±0.5) kg (10±0.3) kg (10±0.2) kg
A. 0.8 kg B. 0.6 kg
C. 0.4 kg D. 0.5 kg
A
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 列式并计算:
(1)和是-2,一个加数是6,求另一个加数;
(2)差是-5,被减数是-7,求减数;
(3)一个数是16,另一个数比16的相反数小-2,求这两个
数的差.
【解】-2-6=-2+(-6)=-8.
【解】-7-(-5)=-7+5=-2.
(3)16 [-16-(-2)]=16-(-14)=16+14=30.
【解】 16-
=16-(-14)=16+14=30.
1
2
3
4
5
6
7
8
9
10
11
12
13
8. [新考向·知识情境化]如图是某一矿井的示意图,以地面为
基准,A点的高度是+4.2 m,B点的高度为-15.6 m,
C点的高度为-30.5 m.请问:A点比B点高多少米?B
点比C点高多少米?
【解】+4.2-(-15.6)=4.2+15.6=19.8(m).
-15.6-(-30.5)=-15.6+30.5=14.9(m).
答:A点比B点高19.8 m,B点比C点高14.9 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
9. 两数a,b在数轴上对应点的位置如图所示,下列判断正
确的是( B )
A. a+b>0 B. a+b<0
C. a-b<0 D. |a|-|b|>0
B
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图的算法思路源于我国古代数学名著《九章算术》中
的“更相减损术”,按照这个算法,如果输入a,b的
值分别为3,8,那么输出a的值为 .
1
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 在计算两个数的减法-3 -■时,由于不小心,减数被
墨水污染.
(1)嘉淇误将-3 后面的“-”看成了“+”,从而算得
结果为5 ,请求出被墨水污染的减数;
【解】由题意得,被墨水污染的减数为5 -
=5 +3 =9 .
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)请你正确计算此题.
【解】-3 -9 =-13 .
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 小明在电脑中设置了一个有理数的运算程序,输入数
a,加*键,再输入数b,就可以得到运算:a*b=(a-b)
-|b-a|.
(1)求(-3)*2的值;
(2)求(3*4)*(-5)的值.
【解】(-3)*2=(-3-2)-|2-(-3)|=-5-5
=-10.
(2)3*4=(3-4)-|4-3|=-2,(-2)*(-5)=
[(-2)-(-5)]-|-5-(-2)|=0,
所以(3*4)*(-5)=0.
【解】3*4=(3-4)-|4-3|=-2,(-2)*(-5)=
-|-5-(-2)|=0,
所以(3*4)*(-5)=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [新考法·阅读类比法]阅读材料:点A,B在数轴上分别
表示有理数a,b.在数轴上A,B两点之间的距离=|
a-b|.所以式子|x-3|的几何意义是数轴上表示有
理数x的点与表示有理数3的点之间的距离;同理|x-
4|也可理解为x与4两数在数轴上所对应的两点之间的
距离.
试探索:
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)若|x-2|=5,则x的值是 ;
(2)同理|x-5|+|x+3|=8表示数轴上有理数x所
对应的点到5和-3所对应的两点的距离之和为8,则
所有符合条件的整数x的和为 ;
-3或7
9
1
2
3
4
5
6
7
8
9
10
11
12
13
(3)由以上探索猜想,若点P表示的数为x,当点P在数
轴上的什么位置时,|x+1|+|x-3|+|x-
5|有最小值?如果有,直接写出最小值.
【解】由题意可得,该算式表示数轴上点P到表示-
1,3,5的点的距离之和,可得当点P在数轴上表示3
的点处时,|x+1|+|x-3|+|x-5|有最小
值,最小值为6.
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
2.2 有理数的减法
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的减法
课程目标
深刻理解有理数减法的意义,熟练掌握有理数减法法则。
能够准确无误地运用有理数减法法则进行各类计算。
学会灵活运用运算技巧,简化有理数减法运算过程。
能够运用有理数减法知识,有效解决实际生活中的数学问题。
有理数减法的定义
有理数减法是已知两个有理数加数的和与其中一个加数,求另一个加数的运算,它是加法的逆运算。例如,已知\(a + b = c\),那么\(c - b = a\),这里\(c - b\)就是有理数减法运算。
有理数减法法则
减去一个数,等于加上这个数的相反数。用式子表示为:\(a - b = a + (-b)\) 。这其中有 “两变一不变”:
两变:
运算符号改变,减法运算变为加法运算。
减数改变,减数变成它的相反数。
一不变:被减数保持不变。
有理数减法运算步骤
将减法运算转化为加法运算,即把减号变为加号,同时将减数变为它的相反数。
按照有理数加法法则进行计算。先确定和的符号,再计算和的绝对值。
实例演示
计算\(5 - 3\):
依据法则,转化为加法:\(5 - 3 = 5 + (-3)\) 。
按照加法法则计算:因为\(5\)是正数,\(-3\)是负数,异号两数相加,\(5\)的绝对值大于\(-3\)的绝对值,所以取\(5\)的符号为正号,并用\(5\)的绝对值减去\(-3\)的绝对值,即\(5 - 3 = 5 + (-3) = +(5 - 3) = 2\) 。
计算\(3 - 5\):
转化为加法:\(3 - 5 = 3 + (-5)\) 。
按加法法则计算:\(3\)是正数,\(-5\)是负数,异号两数相加,\(-5\)的绝对值大于\(3\)的绝对值,所以取\(-5\)的符号为负号,并用\(-5\)的绝对值减去\(3\)的绝对值,即\(3 - 5 = 3 + (-5) = -(5 - 3) = -2\) 。
有理数减法运算技巧
凑整法:若被减数和减数接近某个整数,可将减数凑整,简化计算。例如计算\(45 - 29.5\),可将\(29.5\)看作\(30\),先算\(45 - 30 = 15\),因为多减了\(0.5\),所以结果要加上\(0.5\),即\(45 - 29.5 = 15 + 0.5 = 15.5\) 。
运用运算律:在多个有理数加减混合运算中,可利用加法交换律和结合律调整数的顺序或组合。例如计算\(15 + 23 - 10 - 13\),可利用交换律和结合律变形为\((15 - 10) + (23 - 13) = 5 + 10 = 15\) 。
分数运算技巧:进行分数减法运算时,若分母不同,需先通分,化为同分母分数再相减。例如计算\(\frac{3}{4} - \frac{1}{3}\),先通分,\(4\)和\(3\)的最小公倍数是\(12\),则\(\frac{3}{4} - \frac{1}{3} = \frac{3 3}{4 3} - \frac{1 4}{3 4} = \frac{9}{12} - \frac{4}{12} = \frac{9 - 4}{12} = \frac{5}{12}\) 。
实际应用举例
温度问题:某天最高气温是\(8 \),最低气温是\(-3 \),这天的温差是多少?
温差 = 最高气温 - 最低气温,即\(8 - (-3)\) 。
根据减法法则,转化为加法:\(8 - (-3) = 8 + 3 = 11( )\) ,所以这天的温差是\(11 \) 。
海拔问题:A 地海拔高度为\(200\)米,B 地海拔高度为\(-50\)米,A 地比 B 地高多少米?
可列式为\(200 - (-50)\) 。
转化为加法:\(200 - (-50) = 200 + 50 = 250\)(米),即 A 地比 B 地高\(250\)米。
经济问题:某商店上周盈利\(300\)元,本周盈利\(-50\)元,上周比本周多盈利多少元?
多盈利的金额 = 上周盈利 - 本周盈利,即\(300 - (-50)\) 。
转化为加法计算:\(300 - (-50) = 300 + 50 = 350\)(元),所以上周比本周多盈利\(350\)元。
课堂练习
计算下列各题:
\(7 - 4\)
\((-7) - 4\)
\(7 - (-4)\)
\((-7) - (-4)\)
\(0 - 5\)
\(5 - 0\)
运用运算技巧计算:
\(35 - 19.8\)
\(12 + 25 - 18 - 12\)
\(\frac{5}{6} - \frac{1}{4}\)
解决实际问题:
潜水员在水下\(30\)米处,记作\(-30\)米,上升\(15\)米后,他现在的位置是多少米?
总结
有理数减法法则是 “减去一个数,等于加上这个数的相反数”,计算时要遵循 “两变一不变” 原则。
运算时先将减法转化为加法,再按加法法则计算。
灵活运用凑整法、运算律和分数运算技巧等,可以使计算更简便。
有理数减法在温度、海拔、经济等实际生活场景中有广泛应用,要学会将实际问题转化为数学问题并解决。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数的减法法则,能熟练进行有理数的减法运算,提
高运算能力。
2.能把有理数的加减混合运算转化成加法运算,体会转化思想。
3.能将和式中的括号和加号省略,并利用加法运算律进行计算。
4.能运用有理数的加减法解决简单的实际问题,形成应用意识。
1.有理数的减法法则:减去一个数,等于加上这个数的相反数。
用字母表示: 。
2.将减法转化为加法时要注意“两变一不变”:
“两变”是指运算符号“-”需要变成“ ”,减数变成它的
相反数;“一不变”是指被减数不变。
(1)任何数减去0,仍得这个数;0减去一个数,得这个数的相反数。
(2)减法没有交换律,被减数与减数的位置不能改变。
教材延伸 两数相减,差的符号的确定
(1)较大的数-较小的数正数,即若,则 ;反之,若,则 。
(2)较小的数-较大的数负数,即若,则 ;反之,若,则 。
(3)相等的两个数的差为0,即若,则 ;反之,若,则 。
上述结论也常用于“作差法比较两个有理数的大小”。
典例1 计算:
(1) ;
解: 。
(2) ;
解: 。
(3) ;
解: 。
(4) ;
解: 。
(5) ;
解: 。
一个数减一个正数,所得的差小于这个数;
一个数减一个负数,所得的差大于这个数。
(6) 。
解: 。
有理数减法运算“三步曲”
(1)把减号变为加号(改变运算符号);
(2)把减数变为它的相反数(改变性质符号);
(3)按照加法运算的步骤进行运算。
我们可以把算式 中各个加数的括号和括号
前面的加号省略,写成,这个算式仍可看作和式,
读作“正 、负 与正的和”(按式子表示的意义读),或
者读作“减加 ”(按运算的意义读)。这样给算法的选择
和书写带来方便。
典例2 把写成省略“ ”号和
括号的形式,并写出它的读法。
解:
。
读作“负6、正7、负9、正3的和”,或者读作“负6加7减9加3”。
省略的是运算符号,性质符号必须保留。
第1个数前面的符号是性质符号。
有理数加减混合运算的步骤:
(1)遇减化加:利用减法法则,将减法转化为加法;
(2)运用加法交换律和结合律,简化运算;
(3)求出结果。
(1) ;
解:
(把减法转化为加法)
(加法交换律)
(加法结合律)
。
交换加数的位置时,必须连同加数前面的符号一起交换。
典例3 计算:
(2) 。
解:
(将减法转化成加法)
(加法交换律)
(加法结合律)
。
知识过关
减去一个数,等于加上这个数的 相反数 .
相反数
有理数的减法法则
1. [2024·天津]计算3-(-3)的结果是( D )
A. -6 B. 0 C. 3 D. 6
D
1
2
3
4
5
6
7
8
9
10
11
12
13
2. [2024·石家庄期末]下列算式:①2-(-2)=0;②(-3)-
(+3)=0;③(-3)-|-3|=0;④0-(-1)=1.其中正
确的有( A )
A. 1个 B. 2个
C. 3个 D. 4个
A
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 下列说法:
①减去一个负数等于加上这个数的相反数;
②正数减负数,差为正数;
③零减去一个数,仍得这个数;
④两数相减,差一定小于被减数;
⑤两数相减,差不一定小于被减数;
⑥互为相反数的两数相减得零.
其中正确的有( B )
A. 2个 B. 3个
C. 4个 D. 5个
B
1
2
3
4
5
6
7
8
9
10
11
12
13
4. [母题 教材P42作业题T2]计算:
(1)-2-(+10);
(2)0-(-3.6);
【解】-2-(+10)
=-2+(-10)
=-12.
【解】0-(-3.6)
=0+3.6
=3.6.
1
2
3
4
5
6
7
8
9
10
11
12
13
(3)(-30)-(-6);
(4)(+13)-(+16).
【解】(-30)-(-6)
=(-30)+6
=-24.
【解】(+13)-(+16)
=+13+(-16)
=-3.
1
2
3
4
5
6
7
8
9
10
11
12
13
有理数减法法则的应用
5. [新考向·知识情境化]圆圆想了解某地某天的天气情况,在
某气象网站查询到该地这天的最低气温为-6 ℃,最高气
温为2 ℃,则该地这天的温差(最高气温与最低气温的差)
为( D )
A. -8 ℃ B. -4 ℃
C. 4 ℃ D. 8 ℃
D
1
2
3
4
5
6
7
8
9
10
11
12
13
6. [情境题·生活应用]某商店出售三种不同品牌的大米,米袋
上分别标有质量如表.现从中任意拿出两袋不同品牌的大
米,这两袋大米的质量最多相差( A )
大米种类 A品牌大米 B品牌大米 C品牌大米
质量标示 (10±0.5) kg (10±0.3) kg (10±0.2) kg
A. 0.8 kg B. 0.6 kg
C. 0.4 kg D. 0.5 kg
A
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 列式并计算:
(1)和是-2,一个加数是6,求另一个加数;
(2)差是-5,被减数是-7,求减数;
(3)一个数是16,另一个数比16的相反数小-2,求这两个
数的差.
【解】-2-6=-2+(-6)=-8.
【解】-7-(-5)=-7+5=-2.
(3)16 [-16-(-2)]=16-(-14)=16+14=30.
【解】 16-
=16-(-14)=16+14=30.
1
2
3
4
5
6
7
8
9
10
11
12
13
8. [新考向·知识情境化]如图是某一矿井的示意图,以地面为
基准,A点的高度是+4.2 m,B点的高度为-15.6 m,
C点的高度为-30.5 m.请问:A点比B点高多少米?B
点比C点高多少米?
【解】+4.2-(-15.6)=4.2+15.6=19.8(m).
-15.6-(-30.5)=-15.6+30.5=14.9(m).
答:A点比B点高19.8 m,B点比C点高14.9 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
9. 两数a,b在数轴上对应点的位置如图所示,下列判断正
确的是( B )
A. a+b>0 B. a+b<0
C. a-b<0 D. |a|-|b|>0
B
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图的算法思路源于我国古代数学名著《九章算术》中
的“更相减损术”,按照这个算法,如果输入a,b的
值分别为3,8,那么输出a的值为 .
1
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 在计算两个数的减法-3 -■时,由于不小心,减数被
墨水污染.
(1)嘉淇误将-3 后面的“-”看成了“+”,从而算得
结果为5 ,请求出被墨水污染的减数;
【解】由题意得,被墨水污染的减数为5 -
=5 +3 =9 .
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)请你正确计算此题.
【解】-3 -9 =-13 .
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 小明在电脑中设置了一个有理数的运算程序,输入数
a,加*键,再输入数b,就可以得到运算:a*b=(a-b)
-|b-a|.
(1)求(-3)*2的值;
(2)求(3*4)*(-5)的值.
【解】(-3)*2=(-3-2)-|2-(-3)|=-5-5
=-10.
(2)3*4=(3-4)-|4-3|=-2,(-2)*(-5)=
[(-2)-(-5)]-|-5-(-2)|=0,
所以(3*4)*(-5)=0.
【解】3*4=(3-4)-|4-3|=-2,(-2)*(-5)=
-|-5-(-2)|=0,
所以(3*4)*(-5)=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [新考法·阅读类比法]阅读材料:点A,B在数轴上分别
表示有理数a,b.在数轴上A,B两点之间的距离=|
a-b|.所以式子|x-3|的几何意义是数轴上表示有
理数x的点与表示有理数3的点之间的距离;同理|x-
4|也可理解为x与4两数在数轴上所对应的两点之间的
距离.
试探索:
1
2
3
4
5
6
7
8
9
10
11
12
13
(1)若|x-2|=5,则x的值是 ;
(2)同理|x-5|+|x+3|=8表示数轴上有理数x所
对应的点到5和-3所对应的两点的距离之和为8,则
所有符合条件的整数x的和为 ;
-3或7
9
1
2
3
4
5
6
7
8
9
10
11
12
13
(3)由以上探索猜想,若点P表示的数为x,当点P在数
轴上的什么位置时,|x+1|+|x-3|+|x-
5|有最小值?如果有,直接写出最小值.
【解】由题意可得,该算式表示数轴上点P到表示-
1,3,5的点的距离之和,可得当点P在数轴上表示3
的点处时,|x+1|+|x-3|+|x-5|有最小
值,最小值为6.
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
