2.3 有理数的乘法 课件(共52张PPT)
文档属性
| 名称 | 2.3 有理数的乘法 课件(共52张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 8.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览









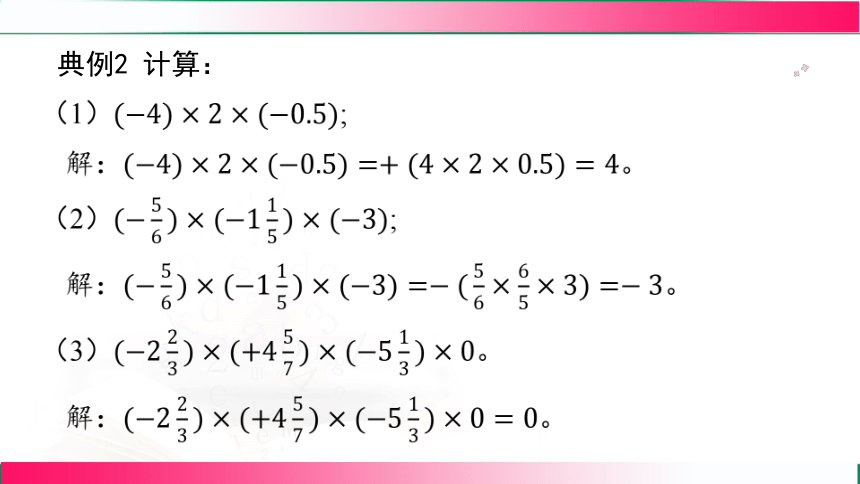


文档简介
2.3 有理数的乘法
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的乘法
课程目标
理解有理数乘法的意义,掌握有理数乘法的法则。
能够熟练运用有理数乘法法则进行计算。
了解有理数乘法的运算律,并能运用运算律简化计算。
学会运用有理数乘法解决实际问题。
有理数乘法的定义
有理数的乘法是求几个相同有理数相加的简便运算。例如,3 个(-2)相加,即(-2)+(-2)+(-2),可以用乘法表示为(-2)×3。
有理数乘法法则
同号两数相乘:取正号,并把绝对值相乘。
例如:(+3)×(+5)= +(3×5)= +15;(-3)×(-5)= +(3×5)= +15 。
异号两数相乘:取负号,并把绝对值相乘。
例如:(+3)×(-5)= -(3×5)= -15;(-3)×(+5)= -(3×5)= -15 。
任何数与 0 相乘:都得 0。
例如:0×(+5)= 0;0×(-5)= 0 。
有理数乘法运算步骤
确定积的符号:根据两个乘数的符号,按照乘法法则确定积的符号。
计算积的绝对值:将两个乘数的绝对值相乘。
写出结果:将确定的符号和计算出的绝对值组合起来,得到乘法的结果。
实例演示
计算(-4)×(-5):
确定符号:两个乘数都是负数,同号相乘取正号。
计算绝对值:4×5 = 20。
写出结果:(-4)×(-5)= +20 = 20 。
计算(-4)×5:
确定符号:一个乘数是负数,一个是正数,异号相乘取负号。
计算绝对值:4×5 = 20。
写出结果:(-4)×5 = -20 。
计算 0×(-6):
根据法则,任何数与 0 相乘都得 0,所以 0×(-6)= 0 。
多个有理数相乘的法则
几个不是 0 的数相乘,积的符号由负因数的个数决定:
当负因数的个数是偶数时,积是正数;
当负因数的个数是奇数时,积是负数。
几个数相乘,如果其中有一个因数是 0,积就为 0。
例如:(-2)×(-3)×(-4),负因数的个数是 3 个(奇数),所以积是负数,绝对值为 2×3×4 = 24,即(-2)×(-3)×(-4)= -24 ;(-2)×(-3)×4,负因数的个数是 2 个(偶数),所以积是正数,绝对值为 2×3×4 = 24,即(-2)×(-3)×4 = 24 ;(-2)×0×(-3)= 0 。
有理数乘法的运算律
乘法交换律:两个数相乘,交换因数的位置,积相等。用字母表示为:a×b = b×a 。例如:(-3)×4 = 4×(-3)= -12 。
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。用字母表示为:(a×b)×c = a×(b×c)。例如:[(-2)×3]×(-4)=(-2)×[3×(-4)] = 24 。
乘法分配律:一个数与两个数的和相乘,等于把这个数分别与这两个数相乘,再把积相加。用字母表示为:a×(b + c)= a×b + a×c 。例如:(-5)×(2 + 3)=(-5)×2 +(-5)×3 = -10 +(-15)= -25 。
运用运算律简化计算
在进行多个有理数相乘时,合理运用乘法交换律、结合律和分配律,可以使计算更加简便。
例如:计算(-8)×(-5)×(-0.125),运用乘法交换律可得(-8)×(-0.125)×(-5)= 1×(-5)= -5 ;计算 12×(\(\frac{1}{3}\) - \(\frac{1}{4}\)),运用乘法分配律可得 12×\(\frac{1}{3}\) - 12×\(\frac{1}{4}\) = 4 - 3 = 1 。
实际应用举例
某商店每件商品亏损 2 元,卖出 5 件这样的商品,总的亏损情况如何?
可列式为:(-2)×5 = -10(元),即总的亏损 10 元。
一个水库的水位每小时下降 3 厘米,4 小时后水位下降了多少厘米?
列式为:(-3)×4 = -12(厘米),即水位下降了 12 厘米。
一片森林,每天吸收二氧化碳 5 吨,那么 3 天吸收多少吨二氧化碳?一周(7 天)呢?
3 天吸收:5×3 = 15(吨);一周吸收:5×7 = 35(吨)。
课堂练习
计算下列各题:
(+6)×(+7)
(-6)×(-7)
(+6)×(-7)
(-6)×(+7)
0×(-8)
运用运算律计算:
(-12)×(-\(\frac{1}{3}\) + \(\frac{1}{4}\))
(-25)×(-4)×(-6)
总结
有理数乘法法则是进行有理数乘法运算的依据,要根据乘数的符号情况正确应用法则。
计算时要先确定符号,再计算绝对值。多个有理数相乘,需先看有无 0 因数,再确定负因数个数以定符号。
乘法交换律、结合律和分配律可以简化有理数乘法的计算,在实际运算中要灵活运用。
有理数乘法在生活中有着广泛的应用,能帮助我们解决一些实际的亏损、水位变化等问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数的乘法法则及多个有理数相乘的符号法则,能
熟练进行有理数的乘法运算,提高运算能力。
2.理解有理数的倒数的意义,会求一个非零有理数的倒数。
3.理解有理数乘法的交换律、结合律和分配律,能运用乘法
运算律简化运算。
4.能运用有理数的乘法解决简单的实际问题,形成应用意识。
一个数与1相乘等于它本身,与?1 相乘等于它的相反数。
?
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与零相乘,积为零。
典例1 计算:
(1)(?2)× (?3) ;
?
解:(?2)×(?3)
=+(2×3) (先确定积的符号,再将绝对值相乘)
=6 。
?
必须带括号
(2)(+313)×(?35) ;
?
解:(+313)×(?35)
=?(313×35)
=?(103×35) (若因数中有带分数,则把带分数化成假分数)
=?2 。
?
(3)(?2?025)×0 ;
?
解:(?2?025)×0=0 。(任何数与零相乘,积为零)
?
(4)(?123)×1.8 。
?
解:(?123)×1.8
=?123×1.8 (分数与小数相乘时,要根据这两个数的特点
统一化成分数或小数)
=?53×95
=?3 。
?
1.多个不为0的有理数相乘时,积的符号由负乘数的个数决定。
(1)当负乘数的个数为奇数时,积的符号为负;
(2)当负乘数的个数为偶数时,积的符号为正。
可简记为“奇负偶正”。
2.多个有理数相乘,若其中有一个乘数为0,则积为0,即
“有0得0”。
3.多个有理数相乘的步骤:
(1)看:看乘数是否有“0”,若有,则积为0。
(2)定:按照负乘数的个数(“奇负偶正”)确定积的符号。
(3)求:把几个乘数的绝对值相乘。
典例2 计算:
(1)(?4)×2×(?0.5) ;
?
解:(?4)×2×(?0.5)=+(4×2×0.5)=4 。
?
(2)(?56)×(?115)×(?3) ;
?
解:(?56)×(?115)×(?3)=?(56×65×3)=?3 。
?
(3)(?223)×(+457)×(?513)×0 。
?
解:(?223)×(+457)×(?513)×0=0 。
?
1.倒数的定义:若两个有理数的乘积为1,就称这两个有理数
互为倒数。0没有倒数。
倒数是两个数之间的一种关系,其中一个数叫作另一
个数的倒数,单独的一个数不能称为倒数。
2.倒数的性质:如果????,????互为倒数,那么????×????=1 。
3.倒数的判定:若????×????=1,则????,???? 两数互为倒数。
?
4.求倒数的方法:
类型
方法
示例
非零整数???? 的
倒数
用这个数作分母,1作
分子,即直接写成1 ???? 。
3的倒数是1 3 ,?3 的倒
数是?1 3 。
分数???????? 的倒数
把这个分数的分子和分
母交换位置,即???? ???? 的倒
数是???? ???? 。
?3 4 的倒数是?4 3 ,9 5 的倒数是5 9 。
类型
方法
示例
类型
方法
示例
带分数的倒数
先把带分数化成假分
数,再交换分子和分母
的位置。
?112=?32,所以?112
的倒数是?23 。
小数的倒数
先把小数化成分数,再
求其倒数。
?0.5=?12 ,所以?0.5
的倒数是?2 。
类型
方法
示例
带分数的倒数
先把带分数化成假分
数,再交换分子和分母
的位置。
小数的倒数
先把小数化成分数,再
求其倒数。
相反数与倒数的不同点
表示
性质
判定
符号
相反数
???? 的相反
数是????? 。
若????,???? 互为相
反数,则
????+????=0 。
若????+????=0 ,
则????,???? 互为相反数。
正数的相反数是负数;负数的相反数是正数;0的相反数是0。
倒数
????(????≠0) 的倒数是1???? 。
若????,???? 互为倒
数,则
????×????=1 ..。。..。
若????×????=1, 则????,???? 互为倒数。
正数的倒数是正数;负数的倒数
是负数;0没有
倒数。
表示
性质
判定
符号
相反数
正数的相反数是负数;负数的相反数是正数;0的相反数是0。
倒数
正数的倒数是正数;负数的倒数
是负数;0没有
倒数。
典例3 求下列各数的倒数:
(1)1;
解:1 的倒数是1。
(2)?53 ;
?
解:?53 的倒数是?35 。
?
(3)?213 ;
?
解:因为?213=?73,所以?213的倒数是?37 。
?
(4)?2.5 ;
?
解:因为?2.5=?52,所以?2.5的倒数是?25 。
?
(5)25% 。
?
解:因为25%=0.25=14,所以25% 的倒数是4。
?
在有理数运算中,乘法的交换律、结合律和分配律同样成立。
运算律
文字叙述
用字母表示
示例
乘法交
换律
两个数相乘,交换因
数的位置,积不变。
????×????=
????×???? 。
5×(?6)=
(?6)×5
乘法结
合律
三个数相乘,先把前
两个数相乘,或者先
把后两个数相乘,积
不变。
(????×????)×????=????×(????×????) 。
[7×(?6)]×5=7×[(?6)×5] 。
运算律
文字叙述
用字母表示
示例
乘法交
换律
两个数相乘,交换因
数的位置,积不变。
乘法结
合律
三个数相乘,先把前
两个数相乘,或者先
把后两个数相乘,积
不变。
运算律
文字叙述
用字母表示
示例
分配律
一个数与两个数的和
相乘,等于把这个数
分别与这两个数相
乘,再把积相加。
????×(????+????)=????×????+????×???? 。
5×(?6+7)=5×(?6)+5×7 。
运算律
文字叙述
用字母表示
示例
分配律
一个数与两个数的和
相乘,等于把这个数
分别与这两个数相
乘,再把积相加。
分配律也可以逆用:????×????+????×????=????×(????+????)。
。
?
教材延伸:乘法运算律的推广
(1)乘法交换律与乘法结合律的推广:三个或三个
以上的有理数相乘,任意交换因数的位置,或者任意先把其
中几个因数相乘,积不变。
(2)分配律的推广:一个数与三个或三个以上的数的和
相乘,等于把这个数分别与每一个加数相乘,再把积相加,
即????×(????+????+?+????)=????×????+????×????+?+????×???? 。
?
典例4 计算:
(1)(?0.125)×(?0.05)×8×(?40) ;
?
解:(?0.125)×(?0.05)×8×(?40)
=?(0.125×0.05×8×40) (定符号:奇负偶正)
=?[(0.125×8)×(0.05×40)] (乘法交换律和结合律)
=?(1×2)
=?2 。
?
(2)12×(14?13?12) ;
?
解:12×(14?13?12)
=12×14+12×(?13)+12×(?12) (分配律)
=3?4?6
=?7 。
?
(3)5.01×33 。
?
解:5.01×33=(5+0.01)×33=5×33+0.01×33=
165+0.33=165.33 。
?
利用分配律进行计算时,不要漏乘,不要弄错符号
知识过关
①有理数的乘法法则:(1)两数相乘,同号得? 正 ,异号
得? 负 ,并把? 绝对值 相乘;
(2)任何数与零相乘,积为? 零 .
②多个不为0的有理数相乘时,可以先确定? 积的符号 ,
再将? 绝对值 相乘.
③若两个有理数的乘积为? 1 ,就称这两个有理数互为倒
数;? 0 没有倒数.
正
负
绝对值
零
积的符号
绝对值
1
0
有理数的乘法法则
1. 计算(-3)×2,正确的结果是( D )
A. 6
B. 5
C. -5
D. -6
2. [2024·吉林]若(-3)×□的运算结果为正数,则□内的数
可以为( D )
A. 2
B. 1
C. 0
D. -1
D
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
3. 已知一个数的相反数是2???????? ,另一个数的绝对值是2???????? ,则
这两个数的积为 ?.
?
6或-6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(1)(-15)×????????? ;
?
【解】(-15)×????????? =15×???????? =9.
?
(2)(-2.25)×(+10);
【解】(-2.25)×(+10)=-22.5.
(3)+???????????? ×(+1.2).
?
【解】+???????????? ×(+1.2)=???????? ×???????? =???????? .
?
4. 计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
多个有理数相乘
5. [2023·慈溪月考]4个非零有理数相乘,积的符号是负号,
则这4个有理数中,正数有( A )
A. 1个或3个
B. 1个或2个
C. 2个或4个
D. 3个或4个
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
6. 计算:
(1)(-10)×(-0.2)×2×(-5);
【解】(-10)×(-0.2)×2×(-5)
=-(10×0.2×2×5)=-20.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(2)+???????????? ×????????? ×(-2.5)×????????????? ;
?
【解】+???????????? ×????????? ×(-2.5)×?????????????
=-(????????×???????? ×???????? ×???????????? )=-???????? .
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(3)????????????? ×????????????? ×????????????? ×????????? .
?
【解】????????????? ×????????????? ×????????????? ×?????????
=???????????? ×???????????? ×???????????? ×????????
=???????????? .
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
倒数
7. [2024·陕西]-3的倒数是( A )
A. -????????
B. ????????
C. -3
D. 3
C. -3
D. 3
8. 下列各组数中,互为倒数的是( A )
A. -2和-????????
B. -1和1
C. -???????? 和1.5
D. 0和0
B. -1和1
D. 0和0
A
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
9. 如果ab=-1,则称a,b互为“负倒数”,那么2的“负
倒数”是( D )
A. 2
B. -2
C. ????????
D. -????????
A. 2
B. -2
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
10. 已知|a|=3,|b|=4,且a>b,则ab的值为
( A )
A. ±12
B. ±1
C. 1或-7
D. 7或-1
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
11. 已知两个有理数a,b,如果ab<0且a+b>0,那么
( D )
A. a>0,b>0
B. a<0,b>0
C. a<0,b<0
D. a,b异号,且正数的绝对值较大
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
12. 在整数-3,-1,0,6,2中,若选取两个整数分别填入
“□×△=-6”的□和△中,并使等式成立,则选取后
可以填入“□”的数有( D )
A. 1种
B. 2种
C. 3种
D. 4种
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
13. 有理数a,b,c,d在数轴上对应的点的位置如图,则
abc 0,abcd 0(填“>”或“<”).
>
>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
14. [2024·唐山模拟](1)将9个不同的数分别填入图①中的9个
空格中,使得每行、每列及对角线上各数的和都等于0;
【解】(答案不唯一)如图①所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(2)将9个不同的数分别填入图②中的9个空格中,使得每
行、每列及对角线上各数的积都等于1.
【解】(答案不唯一)如图②所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
15. [新视角·新定义题]若定义一种新的运算“*”,规定有理
数a*b=4ab,如2*3=4×2×3=24.
(1)求3*(-4)的值;
【解】3*(-4)
=4×3×(-4)
=-48.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
【解】(-2)*(6*3)
=(-2)*(4×6×3)
=(-2)*72
=4×(-2)×(72)
=-576.
(2)求(-2)*(6*3)的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
谢谢观看!
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的乘法
课程目标
理解有理数乘法的意义,掌握有理数乘法的法则。
能够熟练运用有理数乘法法则进行计算。
了解有理数乘法的运算律,并能运用运算律简化计算。
学会运用有理数乘法解决实际问题。
有理数乘法的定义
有理数的乘法是求几个相同有理数相加的简便运算。例如,3 个(-2)相加,即(-2)+(-2)+(-2),可以用乘法表示为(-2)×3。
有理数乘法法则
同号两数相乘:取正号,并把绝对值相乘。
例如:(+3)×(+5)= +(3×5)= +15;(-3)×(-5)= +(3×5)= +15 。
异号两数相乘:取负号,并把绝对值相乘。
例如:(+3)×(-5)= -(3×5)= -15;(-3)×(+5)= -(3×5)= -15 。
任何数与 0 相乘:都得 0。
例如:0×(+5)= 0;0×(-5)= 0 。
有理数乘法运算步骤
确定积的符号:根据两个乘数的符号,按照乘法法则确定积的符号。
计算积的绝对值:将两个乘数的绝对值相乘。
写出结果:将确定的符号和计算出的绝对值组合起来,得到乘法的结果。
实例演示
计算(-4)×(-5):
确定符号:两个乘数都是负数,同号相乘取正号。
计算绝对值:4×5 = 20。
写出结果:(-4)×(-5)= +20 = 20 。
计算(-4)×5:
确定符号:一个乘数是负数,一个是正数,异号相乘取负号。
计算绝对值:4×5 = 20。
写出结果:(-4)×5 = -20 。
计算 0×(-6):
根据法则,任何数与 0 相乘都得 0,所以 0×(-6)= 0 。
多个有理数相乘的法则
几个不是 0 的数相乘,积的符号由负因数的个数决定:
当负因数的个数是偶数时,积是正数;
当负因数的个数是奇数时,积是负数。
几个数相乘,如果其中有一个因数是 0,积就为 0。
例如:(-2)×(-3)×(-4),负因数的个数是 3 个(奇数),所以积是负数,绝对值为 2×3×4 = 24,即(-2)×(-3)×(-4)= -24 ;(-2)×(-3)×4,负因数的个数是 2 个(偶数),所以积是正数,绝对值为 2×3×4 = 24,即(-2)×(-3)×4 = 24 ;(-2)×0×(-3)= 0 。
有理数乘法的运算律
乘法交换律:两个数相乘,交换因数的位置,积相等。用字母表示为:a×b = b×a 。例如:(-3)×4 = 4×(-3)= -12 。
乘法结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。用字母表示为:(a×b)×c = a×(b×c)。例如:[(-2)×3]×(-4)=(-2)×[3×(-4)] = 24 。
乘法分配律:一个数与两个数的和相乘,等于把这个数分别与这两个数相乘,再把积相加。用字母表示为:a×(b + c)= a×b + a×c 。例如:(-5)×(2 + 3)=(-5)×2 +(-5)×3 = -10 +(-15)= -25 。
运用运算律简化计算
在进行多个有理数相乘时,合理运用乘法交换律、结合律和分配律,可以使计算更加简便。
例如:计算(-8)×(-5)×(-0.125),运用乘法交换律可得(-8)×(-0.125)×(-5)= 1×(-5)= -5 ;计算 12×(\(\frac{1}{3}\) - \(\frac{1}{4}\)),运用乘法分配律可得 12×\(\frac{1}{3}\) - 12×\(\frac{1}{4}\) = 4 - 3 = 1 。
实际应用举例
某商店每件商品亏损 2 元,卖出 5 件这样的商品,总的亏损情况如何?
可列式为:(-2)×5 = -10(元),即总的亏损 10 元。
一个水库的水位每小时下降 3 厘米,4 小时后水位下降了多少厘米?
列式为:(-3)×4 = -12(厘米),即水位下降了 12 厘米。
一片森林,每天吸收二氧化碳 5 吨,那么 3 天吸收多少吨二氧化碳?一周(7 天)呢?
3 天吸收:5×3 = 15(吨);一周吸收:5×7 = 35(吨)。
课堂练习
计算下列各题:
(+6)×(+7)
(-6)×(-7)
(+6)×(-7)
(-6)×(+7)
0×(-8)
运用运算律计算:
(-12)×(-\(\frac{1}{3}\) + \(\frac{1}{4}\))
(-25)×(-4)×(-6)
总结
有理数乘法法则是进行有理数乘法运算的依据,要根据乘数的符号情况正确应用法则。
计算时要先确定符号,再计算绝对值。多个有理数相乘,需先看有无 0 因数,再确定负因数个数以定符号。
乘法交换律、结合律和分配律可以简化有理数乘法的计算,在实际运算中要灵活运用。
有理数乘法在生活中有着广泛的应用,能帮助我们解决一些实际的亏损、水位变化等问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数的乘法法则及多个有理数相乘的符号法则,能
熟练进行有理数的乘法运算,提高运算能力。
2.理解有理数的倒数的意义,会求一个非零有理数的倒数。
3.理解有理数乘法的交换律、结合律和分配律,能运用乘法
运算律简化运算。
4.能运用有理数的乘法解决简单的实际问题,形成应用意识。
一个数与1相乘等于它本身,与?1 相乘等于它的相反数。
?
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数与零相乘,积为零。
典例1 计算:
(1)(?2)× (?3) ;
?
解:(?2)×(?3)
=+(2×3) (先确定积的符号,再将绝对值相乘)
=6 。
?
必须带括号
(2)(+313)×(?35) ;
?
解:(+313)×(?35)
=?(313×35)
=?(103×35) (若因数中有带分数,则把带分数化成假分数)
=?2 。
?
(3)(?2?025)×0 ;
?
解:(?2?025)×0=0 。(任何数与零相乘,积为零)
?
(4)(?123)×1.8 。
?
解:(?123)×1.8
=?123×1.8 (分数与小数相乘时,要根据这两个数的特点
统一化成分数或小数)
=?53×95
=?3 。
?
1.多个不为0的有理数相乘时,积的符号由负乘数的个数决定。
(1)当负乘数的个数为奇数时,积的符号为负;
(2)当负乘数的个数为偶数时,积的符号为正。
可简记为“奇负偶正”。
2.多个有理数相乘,若其中有一个乘数为0,则积为0,即
“有0得0”。
3.多个有理数相乘的步骤:
(1)看:看乘数是否有“0”,若有,则积为0。
(2)定:按照负乘数的个数(“奇负偶正”)确定积的符号。
(3)求:把几个乘数的绝对值相乘。
典例2 计算:
(1)(?4)×2×(?0.5) ;
?
解:(?4)×2×(?0.5)=+(4×2×0.5)=4 。
?
(2)(?56)×(?115)×(?3) ;
?
解:(?56)×(?115)×(?3)=?(56×65×3)=?3 。
?
(3)(?223)×(+457)×(?513)×0 。
?
解:(?223)×(+457)×(?513)×0=0 。
?
1.倒数的定义:若两个有理数的乘积为1,就称这两个有理数
互为倒数。0没有倒数。
倒数是两个数之间的一种关系,其中一个数叫作另一
个数的倒数,单独的一个数不能称为倒数。
2.倒数的性质:如果????,????互为倒数,那么????×????=1 。
3.倒数的判定:若????×????=1,则????,???? 两数互为倒数。
?
4.求倒数的方法:
类型
方法
示例
非零整数???? 的
倒数
用这个数作分母,1作
分子,即直接写成1 ???? 。
3的倒数是1 3 ,?3 的倒
数是?1 3 。
分数???????? 的倒数
把这个分数的分子和分
母交换位置,即???? ???? 的倒
数是???? ???? 。
?3 4 的倒数是?4 3 ,9 5 的倒数是5 9 。
类型
方法
示例
类型
方法
示例
带分数的倒数
先把带分数化成假分
数,再交换分子和分母
的位置。
?112=?32,所以?112
的倒数是?23 。
小数的倒数
先把小数化成分数,再
求其倒数。
?0.5=?12 ,所以?0.5
的倒数是?2 。
类型
方法
示例
带分数的倒数
先把带分数化成假分
数,再交换分子和分母
的位置。
小数的倒数
先把小数化成分数,再
求其倒数。
相反数与倒数的不同点
表示
性质
判定
符号
相反数
???? 的相反
数是????? 。
若????,???? 互为相
反数,则
????+????=0 。
若????+????=0 ,
则????,???? 互为相反数。
正数的相反数是负数;负数的相反数是正数;0的相反数是0。
倒数
????(????≠0) 的倒数是1???? 。
若????,???? 互为倒
数,则
????×????=1 ..。。..。
若????×????=1, 则????,???? 互为倒数。
正数的倒数是正数;负数的倒数
是负数;0没有
倒数。
表示
性质
判定
符号
相反数
正数的相反数是负数;负数的相反数是正数;0的相反数是0。
倒数
正数的倒数是正数;负数的倒数
是负数;0没有
倒数。
典例3 求下列各数的倒数:
(1)1;
解:1 的倒数是1。
(2)?53 ;
?
解:?53 的倒数是?35 。
?
(3)?213 ;
?
解:因为?213=?73,所以?213的倒数是?37 。
?
(4)?2.5 ;
?
解:因为?2.5=?52,所以?2.5的倒数是?25 。
?
(5)25% 。
?
解:因为25%=0.25=14,所以25% 的倒数是4。
?
在有理数运算中,乘法的交换律、结合律和分配律同样成立。
运算律
文字叙述
用字母表示
示例
乘法交
换律
两个数相乘,交换因
数的位置,积不变。
????×????=
????×???? 。
5×(?6)=
(?6)×5
乘法结
合律
三个数相乘,先把前
两个数相乘,或者先
把后两个数相乘,积
不变。
(????×????)×????=????×(????×????) 。
[7×(?6)]×5=7×[(?6)×5] 。
运算律
文字叙述
用字母表示
示例
乘法交
换律
两个数相乘,交换因
数的位置,积不变。
乘法结
合律
三个数相乘,先把前
两个数相乘,或者先
把后两个数相乘,积
不变。
运算律
文字叙述
用字母表示
示例
分配律
一个数与两个数的和
相乘,等于把这个数
分别与这两个数相
乘,再把积相加。
????×(????+????)=????×????+????×???? 。
5×(?6+7)=5×(?6)+5×7 。
运算律
文字叙述
用字母表示
示例
分配律
一个数与两个数的和
相乘,等于把这个数
分别与这两个数相
乘,再把积相加。
分配律也可以逆用:????×????+????×????=????×(????+????)。
。
?
教材延伸:乘法运算律的推广
(1)乘法交换律与乘法结合律的推广:三个或三个
以上的有理数相乘,任意交换因数的位置,或者任意先把其
中几个因数相乘,积不变。
(2)分配律的推广:一个数与三个或三个以上的数的和
相乘,等于把这个数分别与每一个加数相乘,再把积相加,
即????×(????+????+?+????)=????×????+????×????+?+????×???? 。
?
典例4 计算:
(1)(?0.125)×(?0.05)×8×(?40) ;
?
解:(?0.125)×(?0.05)×8×(?40)
=?(0.125×0.05×8×40) (定符号:奇负偶正)
=?[(0.125×8)×(0.05×40)] (乘法交换律和结合律)
=?(1×2)
=?2 。
?
(2)12×(14?13?12) ;
?
解:12×(14?13?12)
=12×14+12×(?13)+12×(?12) (分配律)
=3?4?6
=?7 。
?
(3)5.01×33 。
?
解:5.01×33=(5+0.01)×33=5×33+0.01×33=
165+0.33=165.33 。
?
利用分配律进行计算时,不要漏乘,不要弄错符号
知识过关
①有理数的乘法法则:(1)两数相乘,同号得? 正 ,异号
得? 负 ,并把? 绝对值 相乘;
(2)任何数与零相乘,积为? 零 .
②多个不为0的有理数相乘时,可以先确定? 积的符号 ,
再将? 绝对值 相乘.
③若两个有理数的乘积为? 1 ,就称这两个有理数互为倒
数;? 0 没有倒数.
正
负
绝对值
零
积的符号
绝对值
1
0
有理数的乘法法则
1. 计算(-3)×2,正确的结果是( D )
A. 6
B. 5
C. -5
D. -6
2. [2024·吉林]若(-3)×□的运算结果为正数,则□内的数
可以为( D )
A. 2
B. 1
C. 0
D. -1
D
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
3. 已知一个数的相反数是2???????? ,另一个数的绝对值是2???????? ,则
这两个数的积为 ?.
?
6或-6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(1)(-15)×????????? ;
?
【解】(-15)×????????? =15×???????? =9.
?
(2)(-2.25)×(+10);
【解】(-2.25)×(+10)=-22.5.
(3)+???????????? ×(+1.2).
?
【解】+???????????? ×(+1.2)=???????? ×???????? =???????? .
?
4. 计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
多个有理数相乘
5. [2023·慈溪月考]4个非零有理数相乘,积的符号是负号,
则这4个有理数中,正数有( A )
A. 1个或3个
B. 1个或2个
C. 2个或4个
D. 3个或4个
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
6. 计算:
(1)(-10)×(-0.2)×2×(-5);
【解】(-10)×(-0.2)×2×(-5)
=-(10×0.2×2×5)=-20.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(2)+???????????? ×????????? ×(-2.5)×????????????? ;
?
【解】+???????????? ×????????? ×(-2.5)×?????????????
=-(????????×???????? ×???????? ×???????????? )=-???????? .
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(3)????????????? ×????????????? ×????????????? ×????????? .
?
【解】????????????? ×????????????? ×????????????? ×?????????
=???????????? ×???????????? ×???????????? ×????????
=???????????? .
?
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
倒数
7. [2024·陕西]-3的倒数是( A )
A. -????????
B. ????????
C. -3
D. 3
C. -3
D. 3
8. 下列各组数中,互为倒数的是( A )
A. -2和-????????
B. -1和1
C. -???????? 和1.5
D. 0和0
B. -1和1
D. 0和0
A
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
9. 如果ab=-1,则称a,b互为“负倒数”,那么2的“负
倒数”是( D )
A. 2
B. -2
C. ????????
D. -????????
A. 2
B. -2
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
10. 已知|a|=3,|b|=4,且a>b,则ab的值为
( A )
A. ±12
B. ±1
C. 1或-7
D. 7或-1
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
11. 已知两个有理数a,b,如果ab<0且a+b>0,那么
( D )
A. a>0,b>0
B. a<0,b>0
C. a<0,b<0
D. a,b异号,且正数的绝对值较大
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
12. 在整数-3,-1,0,6,2中,若选取两个整数分别填入
“□×△=-6”的□和△中,并使等式成立,则选取后
可以填入“□”的数有( D )
A. 1种
B. 2种
C. 3种
D. 4种
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
13. 有理数a,b,c,d在数轴上对应的点的位置如图,则
abc 0,abcd 0(填“>”或“<”).
>
>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
14. [2024·唐山模拟](1)将9个不同的数分别填入图①中的9个
空格中,使得每行、每列及对角线上各数的和都等于0;
【解】(答案不唯一)如图①所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
(2)将9个不同的数分别填入图②中的9个空格中,使得每
行、每列及对角线上各数的积都等于1.
【解】(答案不唯一)如图②所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
15. [新视角·新定义题]若定义一种新的运算“*”,规定有理
数a*b=4ab,如2*3=4×2×3=24.
(1)求3*(-4)的值;
【解】3*(-4)
=4×3×(-4)
=-48.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
【解】(-2)*(6*3)
=(-2)*(4×6×3)
=(-2)*72
=4×(-2)×(72)
=-576.
(2)求(-2)*(6*3)的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
