2.4 有理数的除法 课件(共37张PPT)
文档属性
| 名称 | 2.4 有理数的除法 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览







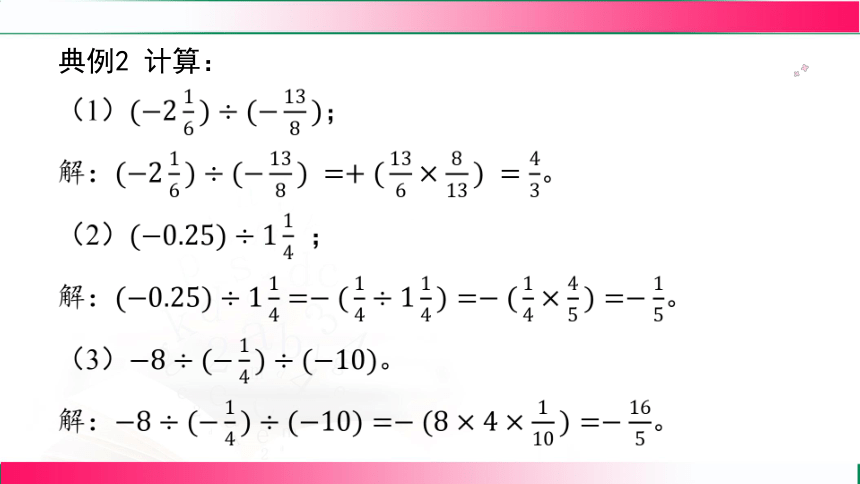




文档简介
(共37张PPT)
2.4 有理数的除法
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的除法
课程目标
理解有理数除法的意义,掌握有理数除法的法则。
能够熟练运用有理数除法法则进行计算,明确除法与乘法的关系。
学会运用有理数除法解决实际问题,掌握相关运算技巧。
有理数除法的定义
有理数的除法是已知两个因数的积与其中一个因数,求另一个因数的运算,它是乘法的逆运算。例如,已知两个数的积是 12,其中一个因数是 3,求另一个因数,就可以用除法表示为 12÷3。
有理数除法法则
同号两数相除:取正号,并把绝对值相除。
例如:(+15)÷(+3)= +(15÷3)= +5;(-15)÷(-3)= +(15÷3)= +5 。
异号两数相除:取负号,并把绝对值相除。
例如:(+15)÷(-3)= -(15÷3)= -5;(-15)÷(+3)= -(15÷3)= -5 。
0 除以任何一个不等于 0 的数:都得 0。
例如:0÷(+5)= 0;0÷(-5)= 0 。
注意:0 不能作除数,因为没有一个数与 0 相乘能得到非 0 的数。
除法与乘法的关系
除以一个不等于 0 的数,等于乘这个数的倒数。用式子表示为:\(a\div b = a\times\frac{1}{b}\)(\(b\neq0\))。
例如:(-12)÷(-4)=(-12)×(-\(\frac{1}{4}\))= 3;(+8)÷(-2)=(+8)×(-\(\frac{1}{2}\))= -4 。
有理数除法运算步骤
确定商的符号:根据被除数和除数的符号,按照除法法则确定商的符号。
计算商的绝对值:将被除数和除数的绝对值相除,或转化为乘法后计算绝对值的积。
写出结果:将确定的符号和计算出的绝对值组合起来,得到除法的结果。
实例演示
计算(-24)÷(-6):
确定符号:被除数和除数都是负数,同号相除取正号。
计算绝对值:24÷6 = 4。
写出结果:(-24)÷(-6)= +4 = 4 。
计算(-18)÷3:
确定符号:被除数是负数,除数是正数,异号相除取负号。
计算绝对值:18÷3 = 6。
写出结果:(-18)÷3 = -6 。
计算 0÷(-7):
根据法则,0 除以任何不等于 0 的数都得 0,所以 0÷(-7)= 0 。
多个有理数相除的运算
多个有理数相除时,先确定商的符号,商的符号由负因数的个数决定:
当负因数的个数为偶数时,商为正;
当负因数的个数为奇数时,商为负。
然后将绝对值相除,或转化为乘法后计算。
例如:(-16)÷(-2)÷(-4),负因数的个数是 2 个(偶数),先确定商为正,再计算绝对值 16÷2÷4 = 2,所以(-16)÷(-2)÷(-4)= -2 ;(-24)÷(-3)÷2,负因数的个数是 2 个(偶数),商为正,24÷3÷2 = 4,所以(-24)÷(-3)÷2 = 4 。
有理数除法运算技巧
分数除法转化:除以一个分数等于乘这个分数的倒数,能简化计算。例如:\(\frac{3}{4}\div\frac{5}{6}=\frac{3}{4}\times\frac{6}{5}=\frac{18}{20}=\frac{9}{10}\) 。
小数除法转化:将小数化为分数再进行除法运算,有时更简便。例如:0.5÷(-\(\frac{1}{4}\))= \(\frac{1}{2}\)÷(-\(\frac{1}{4}\))= \(\frac{1}{2}\)×(-4)= -2 。
利用运算律:在乘除混合运算中,可利用乘法交换律和结合律调整运算顺序。例如:(-8)÷2×(-\(\frac{1}{2}\))=(-8)×(-\(\frac{1}{2}\))÷2 = 4÷2 = 2 。
实际应用举例
平均分配问题:把 - 12 个苹果平均分给 3 个小朋友,每个小朋友得到几个苹果?
可列式为:(-12)÷3 = -4(个),即每个小朋友得到 - 4 个苹果,表示每个小朋友拿出 4 个苹果(或理解为亏欠 4 个)。
速度计算问题:一辆汽车 5 小时行驶了 - 200 千米(负号表示向西行驶),它的平均速度是多少?
平均速度 = 路程 ÷ 时间,列式为:(-200)÷5 = -40(千米 / 小时),即汽车平均每小时向西行驶 40 千米。
浓度问题:把 20 克盐溶解在 - 100 克水中(此处负号仅为举例表示相反量),盐与盐水的质量比的倒数用除法计算是多少?
盐水质量为 20 +(-100)= -80 克,盐与盐水的质量比为 20:(-80)= -\(\frac{1}{4}\),其倒数的除法计算为 1÷(-\(\frac{1}{4}\))= -4 。
课堂练习
计算下列各题:
(+24)÷(+6)
(-36)÷(-9)
(+42)÷(-7)
(-54)÷(+6)
0÷(-12)
运用除法与乘法的关系计算:
(-18)÷(-\(\frac{2}{3}\))
(+\(\frac{3}{4}\))÷(-\(\frac{5}{8}\))
总结
有理数除法法则是进行除法运算的依据,要注意 0 不能作除数。
除法与乘法互为逆运算,除以一个数(非 0)等于乘这个数的倒数,可利用此关系将除法转化为乘法计算。
运算时先确定符号,再计算绝对值,多个数相除要关注负因数的个数。
有理数除法在平均分配、速度、浓度等实际场景中有应用,要能将实际问题转化为数学运算解决。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数的除法法则,能熟练地进行有理数的除法运算。
2.能熟练地进行简单的有理数的加减乘除混合运算,提高运算
能力。
3.能运用有理数的除法解决简单的实际问题,形成应用意识。
有理数的除法法则(一) 两数相除,同号得正,异号得负,
并把绝对值相除;零除以任何一个不等于零的数都得零。
(1)0不能作为除数。(2)两个有理数相除,若商为
1,则这两个数相等;若商为 ,则这两个数互为相反数。
(2) ;
解:
(3) 。
解: 。
典例1 计算:
(1) ;
解: 。
有理数的除法法则(二) 除以一个数(不等于零),等于乘
这个数的倒数。
用字母表示: 。
敲黑板
(1)有理数的除法没有交换律、结合律及分配律。
(2)三个或三个以上的有理数相除,通常把除法运算统一转
化为乘法运算。
典例2 计算:
(1) ;
解: 。
(2) ;
解: 。
(3) 。
解: 。
1.有理数的乘除混合运算:
(1)计算顺序:按照从左往右的顺序计算,有括号的,先计
算括号里面的。
(2)计算方法:先把除法转化为乘法,然后按照有理数的乘
法法则求出结果。
将乘除运算统一为乘法运算后,可以运用乘法交换律、
结合律或分配律简化运算。
2.有理数的加减乘除混合运算的顺序:先算乘除,再算加减,
有括号的先算括号里面的,同级运算中,按照从左往右的顺
序计算。
典例3 计算:
(1) ;
解: 。
(2) 。
解:
。(先算乘除后算加减)
知识过关
①两数相除,同号得 正 ,异号得 负 ,并把 绝对值
相除;零除以任何一个 不等于0 的数都得 0 .
②乘法与除法之间的关系:除以一个数(不等于零),等于 乘
以 这个数的 倒数 .
正
负
绝对值
不等于0
0
乘
以
倒数
有理数的除法法则
1. 计算15÷(-5)的结果是( B )
A. -5 B. -3
C. 3 D. 5
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. [2024·宁波鄞州区调研]-1÷(-5)÷ 的计算结果是
( A )
A. -1
D. 1
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
3. 已知算式“5■(-5)”的值为-1,“■”部分是因被污
染而看不清的运算符号,则该运算符号应该是( D )
A. + B. -
C. × D. ÷
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
4. 列式计算:
(1)一个数与- 的积为 ,求这个数;
【解】 ÷ = × =- .
(2)-2 除以一个数的商为-9,求这个数.
【解】-2 ÷(-9)= × = .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
有理数的乘除混合运算
5. [2024·温州鹿城区月考]计算2÷3× 的结果是( C )
A. -2 B. 2
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
6. 计算:
(1) × ÷0.25;
【解】原式= × ×4
= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(2) ÷(-5)× ;
【解】原式= × ×
=- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(3) × × ÷ .
【解】原式= × × ×
=- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
有理数除法的实际应用
7. 张强和李倩分别用电脑录入同一份稿件,张强录入了这份
稿件的 后,还剩下3 500字,李倩录入的字数占这份稿件
的 ,则李倩录入的字数为( C )
A. 3 500 B. 2 800
C. 3 000 D. 3 200
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
8. [新视角·动态探究题][2024·上海青浦区期末] 如图,机器
人淘淘和巧巧分别站在边长为15米的正方形道路ABCD的
顶点D,B处,他们同时出发,分别以1米每秒和1.5米每
秒的速度沿正方形道路按顺时针方向匀速行走,当淘淘和
巧巧第一次都在正方形的同一顶点处时,经过了多少秒?
( B )
A. 30秒 B. 60秒
C. 90秒 D. 120秒
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
9. 下列说法不正确的是( A )
A. 如果两个数的和为0,那么这两个数的商一定为-1
B. 如果两个数的商为-1,那么这两个数的和一定为0
C. 如果两个数的符号相同,那么这两个数的商一定为正数
D. 如果两个数的商为正数,那么这两个数的符号一定相同
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
10. [2023·无锡滨湖区一模]某同学在计算-16÷a时,误将
“÷”看成“+”,结果是-12,则-16÷a的正确结
果是( D )
A. 6 B. -6
C. 4 D. -4
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
11. 下列说法:①若m满足|m|+m=0,则m<0;②
若|a-b|=b-a,则b>a;③若a+b=0,则
=-1;④若三个有理数a,b,c满足 + +
=1,则 =-1.其中正确的有( A )
A. 1个 B. 2个
C. 3个 D. 4个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【点拨】
①因为|m|+m=0,所以|m|=-m,
所以m≤0,故①错误;
②因为|a-b|=b-a,所以b-a≥0.所以
b≥a,故②错误;
③当a=b=0时,满足a+b=0,但不满足 =-
1,故③错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
④当a,b,c都是正数时, + +
= + + =1+1+1=3,不符合题意;
当a,b,c中有两个正数、一个负数时,不妨设
a,b为正数,则 + + = + + =
1+1-1=1,所以 = =-1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
当a,b,c中有两个负数、一个正数时,不妨设
a,b为负数,则 + + = + +
=-1-1+1=-1,不符合题意;
当a,b,c都是负数时, + +
= + + =-1-1-1=-3,不符合题意.
所以若三个有理数a,b,c满足 + +
=1,则 =-1,故④正确.
A
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
12. 计算6÷ 时,小刚同学的计算过程如下:
解:原式=6÷ +6÷ =-12+18=6.
(1)请你判断小刚同学的计算过程是否正确,若不正确,
请你写出正确的计算过程;
【解】不正确.
正确的计算过程为:原式=6÷ =-36.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【解】因为 ÷ =( - + )×(-
18)=-9+3-2=-8,18÷ =18÷ =
18× = ,
所以原式=-8+ = .
(2)用适当的方法计算 ÷ +18÷ 的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
13. 小丽有5张写着不同数的卡片(如图),请你按要求抽取卡
片,完成下列各题:
从中抽取2张卡片,将卡片上的数相乘,再抽取1张卡
片,用前面两数之积除以第3张卡片上的数得到商.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(1)如何抽取,可使商最大?最大是多少?
【解】抽取的卡片上的数分别为-3,-5,+ ,可
使商最大.最大是(-3)×(-5)÷ =15×4=60.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(2)如何抽取,可使商最小?最小是多少?
【解】抽取的卡片上的数分别为+3,-5,+ ,可
使商最小,最小是(+3)×(-5)÷ =-15×4=
-60.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
14. [新视角·条件开放题]对于四个数“-8,-2,1,3”及
四种运算“+,-,×,÷”,列算式解答:
(1)求这四个数的和;
【解】(-8)+(-2)+1+3=-6.
(2)在这四个数中选出两个数,按要求进行下列计
算,使得:
①两数差的结果最小;
②两数积的结果最大;
【解】①(-8)-3=-11.②(-8)×(-2)=16.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(3)在这四个数中选出三个数,在四种运算中选出两种,
组成一个算式,使运算结果等于没选的那个数.
【解】答案不唯一,符合要求即可.
如:(-8)÷(-2)-3=1或(-8)÷(-2)-1=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
谢谢观看!
2.4 有理数的除法
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的除法
课程目标
理解有理数除法的意义,掌握有理数除法的法则。
能够熟练运用有理数除法法则进行计算,明确除法与乘法的关系。
学会运用有理数除法解决实际问题,掌握相关运算技巧。
有理数除法的定义
有理数的除法是已知两个因数的积与其中一个因数,求另一个因数的运算,它是乘法的逆运算。例如,已知两个数的积是 12,其中一个因数是 3,求另一个因数,就可以用除法表示为 12÷3。
有理数除法法则
同号两数相除:取正号,并把绝对值相除。
例如:(+15)÷(+3)= +(15÷3)= +5;(-15)÷(-3)= +(15÷3)= +5 。
异号两数相除:取负号,并把绝对值相除。
例如:(+15)÷(-3)= -(15÷3)= -5;(-15)÷(+3)= -(15÷3)= -5 。
0 除以任何一个不等于 0 的数:都得 0。
例如:0÷(+5)= 0;0÷(-5)= 0 。
注意:0 不能作除数,因为没有一个数与 0 相乘能得到非 0 的数。
除法与乘法的关系
除以一个不等于 0 的数,等于乘这个数的倒数。用式子表示为:\(a\div b = a\times\frac{1}{b}\)(\(b\neq0\))。
例如:(-12)÷(-4)=(-12)×(-\(\frac{1}{4}\))= 3;(+8)÷(-2)=(+8)×(-\(\frac{1}{2}\))= -4 。
有理数除法运算步骤
确定商的符号:根据被除数和除数的符号,按照除法法则确定商的符号。
计算商的绝对值:将被除数和除数的绝对值相除,或转化为乘法后计算绝对值的积。
写出结果:将确定的符号和计算出的绝对值组合起来,得到除法的结果。
实例演示
计算(-24)÷(-6):
确定符号:被除数和除数都是负数,同号相除取正号。
计算绝对值:24÷6 = 4。
写出结果:(-24)÷(-6)= +4 = 4 。
计算(-18)÷3:
确定符号:被除数是负数,除数是正数,异号相除取负号。
计算绝对值:18÷3 = 6。
写出结果:(-18)÷3 = -6 。
计算 0÷(-7):
根据法则,0 除以任何不等于 0 的数都得 0,所以 0÷(-7)= 0 。
多个有理数相除的运算
多个有理数相除时,先确定商的符号,商的符号由负因数的个数决定:
当负因数的个数为偶数时,商为正;
当负因数的个数为奇数时,商为负。
然后将绝对值相除,或转化为乘法后计算。
例如:(-16)÷(-2)÷(-4),负因数的个数是 2 个(偶数),先确定商为正,再计算绝对值 16÷2÷4 = 2,所以(-16)÷(-2)÷(-4)= -2 ;(-24)÷(-3)÷2,负因数的个数是 2 个(偶数),商为正,24÷3÷2 = 4,所以(-24)÷(-3)÷2 = 4 。
有理数除法运算技巧
分数除法转化:除以一个分数等于乘这个分数的倒数,能简化计算。例如:\(\frac{3}{4}\div\frac{5}{6}=\frac{3}{4}\times\frac{6}{5}=\frac{18}{20}=\frac{9}{10}\) 。
小数除法转化:将小数化为分数再进行除法运算,有时更简便。例如:0.5÷(-\(\frac{1}{4}\))= \(\frac{1}{2}\)÷(-\(\frac{1}{4}\))= \(\frac{1}{2}\)×(-4)= -2 。
利用运算律:在乘除混合运算中,可利用乘法交换律和结合律调整运算顺序。例如:(-8)÷2×(-\(\frac{1}{2}\))=(-8)×(-\(\frac{1}{2}\))÷2 = 4÷2 = 2 。
实际应用举例
平均分配问题:把 - 12 个苹果平均分给 3 个小朋友,每个小朋友得到几个苹果?
可列式为:(-12)÷3 = -4(个),即每个小朋友得到 - 4 个苹果,表示每个小朋友拿出 4 个苹果(或理解为亏欠 4 个)。
速度计算问题:一辆汽车 5 小时行驶了 - 200 千米(负号表示向西行驶),它的平均速度是多少?
平均速度 = 路程 ÷ 时间,列式为:(-200)÷5 = -40(千米 / 小时),即汽车平均每小时向西行驶 40 千米。
浓度问题:把 20 克盐溶解在 - 100 克水中(此处负号仅为举例表示相反量),盐与盐水的质量比的倒数用除法计算是多少?
盐水质量为 20 +(-100)= -80 克,盐与盐水的质量比为 20:(-80)= -\(\frac{1}{4}\),其倒数的除法计算为 1÷(-\(\frac{1}{4}\))= -4 。
课堂练习
计算下列各题:
(+24)÷(+6)
(-36)÷(-9)
(+42)÷(-7)
(-54)÷(+6)
0÷(-12)
运用除法与乘法的关系计算:
(-18)÷(-\(\frac{2}{3}\))
(+\(\frac{3}{4}\))÷(-\(\frac{5}{8}\))
总结
有理数除法法则是进行除法运算的依据,要注意 0 不能作除数。
除法与乘法互为逆运算,除以一个数(非 0)等于乘这个数的倒数,可利用此关系将除法转化为乘法计算。
运算时先确定符号,再计算绝对值,多个数相除要关注负因数的个数。
有理数除法在平均分配、速度、浓度等实际场景中有应用,要能将实际问题转化为数学运算解决。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数的除法法则,能熟练地进行有理数的除法运算。
2.能熟练地进行简单的有理数的加减乘除混合运算,提高运算
能力。
3.能运用有理数的除法解决简单的实际问题,形成应用意识。
有理数的除法法则(一) 两数相除,同号得正,异号得负,
并把绝对值相除;零除以任何一个不等于零的数都得零。
(1)0不能作为除数。(2)两个有理数相除,若商为
1,则这两个数相等;若商为 ,则这两个数互为相反数。
(2) ;
解:
(3) 。
解: 。
典例1 计算:
(1) ;
解: 。
有理数的除法法则(二) 除以一个数(不等于零),等于乘
这个数的倒数。
用字母表示: 。
敲黑板
(1)有理数的除法没有交换律、结合律及分配律。
(2)三个或三个以上的有理数相除,通常把除法运算统一转
化为乘法运算。
典例2 计算:
(1) ;
解: 。
(2) ;
解: 。
(3) 。
解: 。
1.有理数的乘除混合运算:
(1)计算顺序:按照从左往右的顺序计算,有括号的,先计
算括号里面的。
(2)计算方法:先把除法转化为乘法,然后按照有理数的乘
法法则求出结果。
将乘除运算统一为乘法运算后,可以运用乘法交换律、
结合律或分配律简化运算。
2.有理数的加减乘除混合运算的顺序:先算乘除,再算加减,
有括号的先算括号里面的,同级运算中,按照从左往右的顺
序计算。
典例3 计算:
(1) ;
解: 。
(2) 。
解:
。(先算乘除后算加减)
知识过关
①两数相除,同号得 正 ,异号得 负 ,并把 绝对值
相除;零除以任何一个 不等于0 的数都得 0 .
②乘法与除法之间的关系:除以一个数(不等于零),等于 乘
以 这个数的 倒数 .
正
负
绝对值
不等于0
0
乘
以
倒数
有理数的除法法则
1. 计算15÷(-5)的结果是( B )
A. -5 B. -3
C. 3 D. 5
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
2. [2024·宁波鄞州区调研]-1÷(-5)÷ 的计算结果是
( A )
A. -1
D. 1
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
3. 已知算式“5■(-5)”的值为-1,“■”部分是因被污
染而看不清的运算符号,则该运算符号应该是( D )
A. + B. -
C. × D. ÷
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
4. 列式计算:
(1)一个数与- 的积为 ,求这个数;
【解】 ÷ = × =- .
(2)-2 除以一个数的商为-9,求这个数.
【解】-2 ÷(-9)= × = .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
有理数的乘除混合运算
5. [2024·温州鹿城区月考]计算2÷3× 的结果是( C )
A. -2 B. 2
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
6. 计算:
(1) × ÷0.25;
【解】原式= × ×4
= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(2) ÷(-5)× ;
【解】原式= × ×
=- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(3) × × ÷ .
【解】原式= × × ×
=- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
有理数除法的实际应用
7. 张强和李倩分别用电脑录入同一份稿件,张强录入了这份
稿件的 后,还剩下3 500字,李倩录入的字数占这份稿件
的 ,则李倩录入的字数为( C )
A. 3 500 B. 2 800
C. 3 000 D. 3 200
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
8. [新视角·动态探究题][2024·上海青浦区期末] 如图,机器
人淘淘和巧巧分别站在边长为15米的正方形道路ABCD的
顶点D,B处,他们同时出发,分别以1米每秒和1.5米每
秒的速度沿正方形道路按顺时针方向匀速行走,当淘淘和
巧巧第一次都在正方形的同一顶点处时,经过了多少秒?
( B )
A. 30秒 B. 60秒
C. 90秒 D. 120秒
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
9. 下列说法不正确的是( A )
A. 如果两个数的和为0,那么这两个数的商一定为-1
B. 如果两个数的商为-1,那么这两个数的和一定为0
C. 如果两个数的符号相同,那么这两个数的商一定为正数
D. 如果两个数的商为正数,那么这两个数的符号一定相同
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
10. [2023·无锡滨湖区一模]某同学在计算-16÷a时,误将
“÷”看成“+”,结果是-12,则-16÷a的正确结
果是( D )
A. 6 B. -6
C. 4 D. -4
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
11. 下列说法:①若m满足|m|+m=0,则m<0;②
若|a-b|=b-a,则b>a;③若a+b=0,则
=-1;④若三个有理数a,b,c满足 + +
=1,则 =-1.其中正确的有( A )
A. 1个 B. 2个
C. 3个 D. 4个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【点拨】
①因为|m|+m=0,所以|m|=-m,
所以m≤0,故①错误;
②因为|a-b|=b-a,所以b-a≥0.所以
b≥a,故②错误;
③当a=b=0时,满足a+b=0,但不满足 =-
1,故③错误;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
④当a,b,c都是正数时, + +
= + + =1+1+1=3,不符合题意;
当a,b,c中有两个正数、一个负数时,不妨设
a,b为正数,则 + + = + + =
1+1-1=1,所以 = =-1;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
当a,b,c中有两个负数、一个正数时,不妨设
a,b为负数,则 + + = + +
=-1-1+1=-1,不符合题意;
当a,b,c都是负数时, + +
= + + =-1-1-1=-3,不符合题意.
所以若三个有理数a,b,c满足 + +
=1,则 =-1,故④正确.
A
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
12. 计算6÷ 时,小刚同学的计算过程如下:
解:原式=6÷ +6÷ =-12+18=6.
(1)请你判断小刚同学的计算过程是否正确,若不正确,
请你写出正确的计算过程;
【解】不正确.
正确的计算过程为:原式=6÷ =-36.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
【解】因为 ÷ =( - + )×(-
18)=-9+3-2=-8,18÷ =18÷ =
18× = ,
所以原式=-8+ = .
(2)用适当的方法计算 ÷ +18÷ 的值.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
13. 小丽有5张写着不同数的卡片(如图),请你按要求抽取卡
片,完成下列各题:
从中抽取2张卡片,将卡片上的数相乘,再抽取1张卡
片,用前面两数之积除以第3张卡片上的数得到商.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(1)如何抽取,可使商最大?最大是多少?
【解】抽取的卡片上的数分别为-3,-5,+ ,可
使商最大.最大是(-3)×(-5)÷ =15×4=60.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(2)如何抽取,可使商最小?最小是多少?
【解】抽取的卡片上的数分别为+3,-5,+ ,可
使商最小,最小是(+3)×(-5)÷ =-15×4=
-60.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
14. [新视角·条件开放题]对于四个数“-8,-2,1,3”及
四种运算“+,-,×,÷”,列算式解答:
(1)求这四个数的和;
【解】(-8)+(-2)+1+3=-6.
(2)在这四个数中选出两个数,按要求进行下列计
算,使得:
①两数差的结果最小;
②两数积的结果最大;
【解】①(-8)-3=-11.②(-8)×(-2)=16.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
(3)在这四个数中选出三个数,在四种运算中选出两种,
组成一个算式,使运算结果等于没选的那个数.
【解】答案不唯一,符合要求即可.
如:(-8)÷(-2)-3=1或(-8)÷(-2)-1=3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
