2.6 有理数的混合运算 课件(共30张PPT)
文档属性
| 名称 | 2.6 有理数的混合运算 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览





文档简介
(共30张PPT)
2.6 有理数的混合运算
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
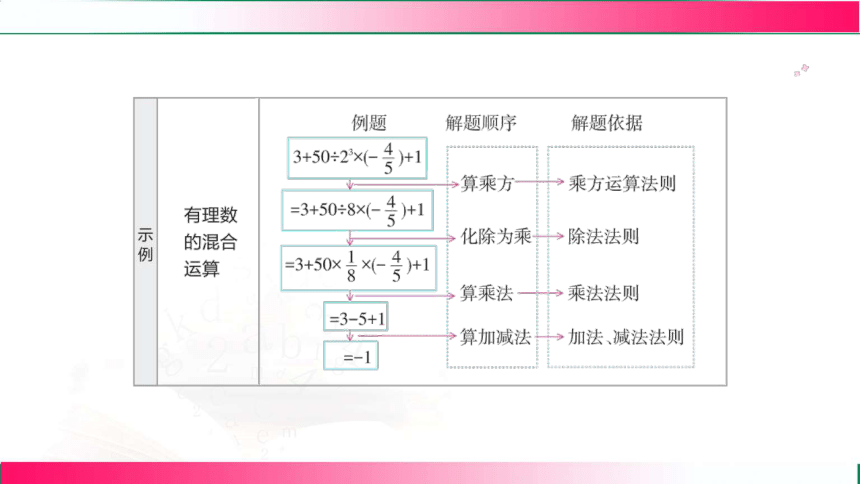
有理数的混合运算
课程目标
掌握有理数混合运算的顺序,能正确进行包含加、减、乘、除、乘方的混合运算。
学会运用运算律简化有理数混合运算,提高运算的准确性和效率。
能够解决与有理数混合运算相关的实际问题,培养数学应用意识。
有理数混合运算的顺序
有理数混合运算的顺序是进行混合运算的核心依据,具体如下:
先算乘方:即先计算各个数的乘方运算,这是运算顺序的第一步。
再算乘除:在完成乘方运算后,按照从左到右的顺序依次进行乘法和除法运算。
最后算加减:乘除运算完成后,再按照从左到右的顺序进行加法和减法运算。
括号优先:如果式子中有括号,要先算括号里面的。括号分为小括号()、中括号 []、大括号 {},计算时要按照从小括号到中括号再到大括号的顺序依次进行。
实例说明
计算\(3 + 2^2\times( - 3)\):
先算乘方:\(2^2=4\)。
再算乘法:\(4\times( - 3)=-12\)。
最后算加法:\(3+( - 12)=-9\)。
计算\(18\div(3 - 6)\times2\):
先算小括号里的:\(3 - 6=-3\)。
再算除法:\(18\div( - 3)=-6\)。
最后算乘法:\(-6\times2=-12\)。
计算\([( - 2)^3 + 5]\div( - 3)\):
先算小括号里的乘方:\(( - 2)^3=-8\)。
再算小括号里的加法:\(-8 + 5=-3\)。
最后算中括号外的除法:\(-3\div( - 3)=1\)。
运算律在混合运算中的应用
在有理数混合运算中,合理运用加法交换律、结合律,乘法交换律、结合律和分配律,能有效简化运算过程。
加法运算律:在只有加减的运算中,可交换加数的位置或结合某些加数,使计算简便。例如,计算\(5+( - 3)+( - 5)+2\),利用加法交换律和结合律可得\([5+( - 5)]+[( - 3)+2]=0+( - 1)=-1\)。
乘法运算律:在乘除混合运算中,可交换因数的位置或结合某些因数。例如,计算\(( - 8)\times5\times( - 0.125)\times( - 2)\),利用乘法交换律和结合律可得\([( - 8)\times( - 0.125)]\times[5\times( - 2)]=1\times( - 10)=-10\)。
乘法分配律:当式子中出现一个数与多个数的和或差相乘时,使用分配律可简化运算。例如,计算\( - 24\times(\frac{1}{3}-\frac{1}{4}+\frac{1}{6})\),利用分配律可得\(-24\times\frac{1}{3}+24\times\frac{1}{4}-24\times\frac{1}{6}=-8 + 6-4=-6\)。
混合运算的易错点
运算顺序错误:忽略乘方、乘除、加减的优先级,或不遵循括号优先原则。例如,计算\(2 + 3\times4\)时,错误地先算加法再算乘法,得到\(5\times4=20\),而正确结果应为\(2 + 12=14\)。
符号错误:在涉及负数的运算中,容易弄错符号。例如,计算\(( - 2)^2\)时,错误地认为结果是\(-4\),而正确结果是\(4\);计算\(-2^2\)时,错误地认为结果是\(4\),而正确结果是\(-4\)。
漏算或重复计算:在步骤较多的运算中,容易漏算某些项或重复计算。例如,计算\(3\times(2 + 5)-4\)时,漏算减法得到\(3\times7=21\),而正确结果是\(21-4=17\)。
混合运算的简化技巧
观察式子结构:在动笔计算前,先观察式子的结构,判断是否能运用运算律简化运算。例如,式子\(100\times3.6 + 100\times6.4\)中,两项都有因数 100,可利用乘法分配律的逆运算简化为\(100\times(3.6 + 6.4)=100\times10=1000\)。
分步计算:对于复杂的混合运算,可分步进行计算,每一步只处理一种运算,减少错误。例如,计算\(10-( - 2)^3\div4\times( - 3)^2\),可先算乘方得到\(10-( - 8)\div4\times9\),再算除法得到\(10 - ( - 2)\times9\),接着算乘法得到\(10 + 18\),最后算加法得到\(28\)。
处理括号:当括号前是 “\(+\)” 号时,去掉括号后,括号内的各项符号不变;当括号前是 “\(-\)” 号时,去掉括号后,括号内的各项符号都要改变。例如,\(5-(3 - 2)=5 - 3 + 2=4\)。
实际应用举例
购物消费问题:小明去超市购物,买了 3 支单价为 5 元的钢笔,2 瓶单价为\(-3\)元的打折饮料(负号表示优惠),又买了一个价格为\(2^3\)元的笔记本,小明一共花了多少钱?
先分别计算各项费用:钢笔总价为\(3\times5 = 15\)元,饮料总价为\(2\times( - 3)=-6\)元,笔记本价格为\(2^3=8\)元。
再计算总花费:\(15+( - 6)+8=17\)元,即小明一共花了 17 元。
工程进度问题:一个工程队第一天完成了总工程的\(\frac{1}{4}\),第二天完成了总工程的\(\frac{1}{3}\),第三天比前两天的总和少完成总工程的\(\frac{1}{6}\),第三天完成了总工程的几分之几?
先算前两天完成的总和:\(\frac{1}{4}+\frac{1}{3}=\frac{3}{12}+\frac{4}{12}=\frac{7}{12}\)。
再算第三天完成的量:\(\frac{7}{12}-\frac{1}{6}=\frac{7}{12}-\frac{2}{12}=\frac{5}{12}\),即第三天完成了总工程的\(\frac{5}{12}\)。
课堂练习
计算下列各题:
\(10-( - 2)^2\times3\)
\(18\div(3 - 6)\times( - 2)\)
\([( - 1)^5 + 2]\times( - 4)\)
运用运算律简化计算:
\(25\times(4 - 0.4)\)
\( - 12\times\frac{1}{3}+12\times\frac{1}{4}-12\times\frac{1}{6}\)
总结
有理数混合运算的顺序是 “先乘方,再乘除,最后加减;有括号的先算括号里的”,必须严格遵循。
合理运用运算律能简化运算,提高效率,但要注意运算符号的变化。
实际应用中,需将问题转化为数学式子,再按照混合运算顺序求解,同时要注意单位和实际意义。
运算时要细心,避免因运算顺序错误、符号错误等导致结果出错,可通过分步计算和检查减少错误。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数混合运算的法则,会进行简单的有理数的混合
运算。
2.能合理地运用运算律简化运算,发展运算能力。
3.会利用有理数的混合运算解决简单实际问题。
一般地,有理数混合运算的法则是:
先算乘方,再算乘除,最后算加减。如有括号,先进行括号里
的运算。
若属于同级运算,则按照从左往右的顺序进行计算。
进行混合运算时,可以灵活运用运算律,但应注意符
号的确定以及运算顺序和方法的选择.例如,可以根据算式的
结构特征,巧用整体思想、拆分消除等技巧,从而使运算准
确、快捷。
知识过关
一般地,计算有理数混合运算时,先算 乘方 ,再
算 乘除 ,最后算 加减 .如有括号,先进行 括号
里的运算.
乘方
乘除
加减
括号
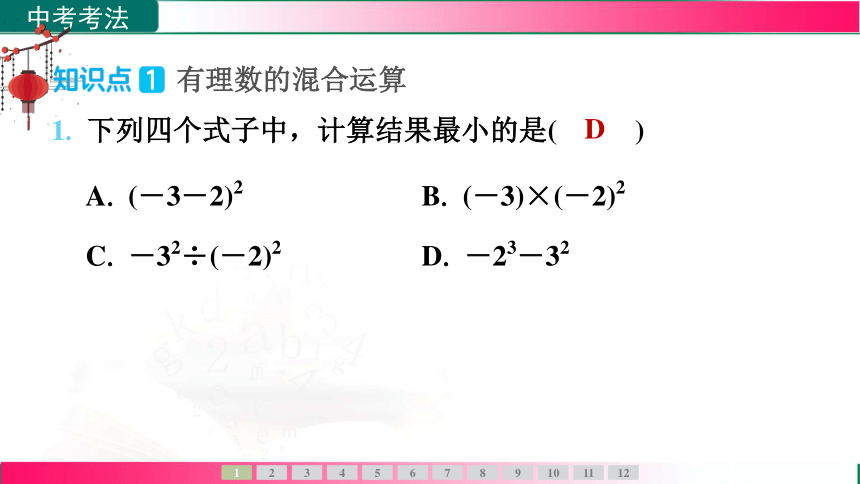
有理数的混合运算
1. 下列四个式子中,计算结果最小的是( D )
A. (-3-2)2 B. (-3)×(-2)2
C. -32÷(-2)2 D. -23-32
D
1
2
3
4
5
6
7
8
9
10
11
12
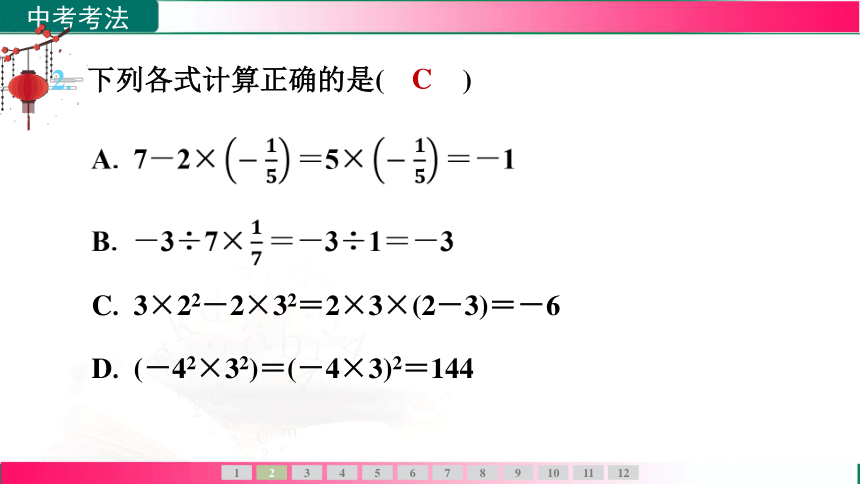
2. 下列各式计算正确的是( C )
C. 3×22-2×32=2×3×(2-3)=-6
D. (-42×32)=(-4×3)2=144
C
1
2
3
4
5
6
7
8
9
10
11
12
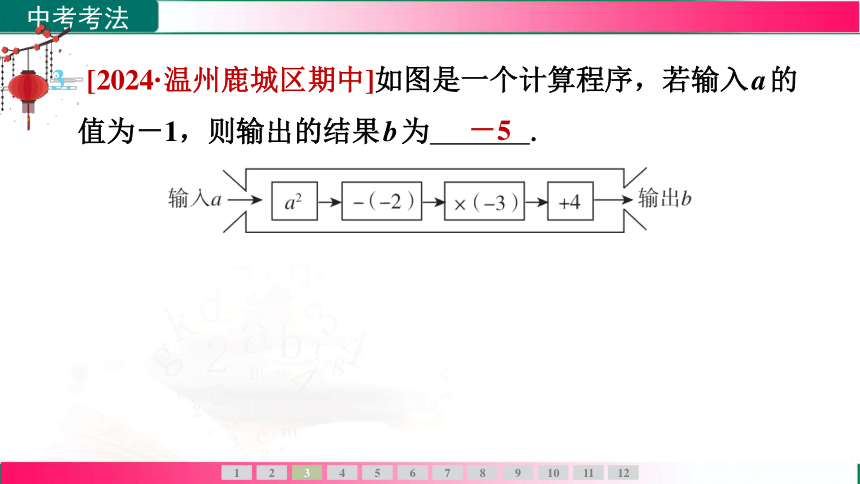
3. [2024·温州鹿城区期中]如图是一个计算程序,若输入a的
值为-1,则输出的结果b为 .
-5
1
2
3
4
5
6
7
8
9
10
11
12
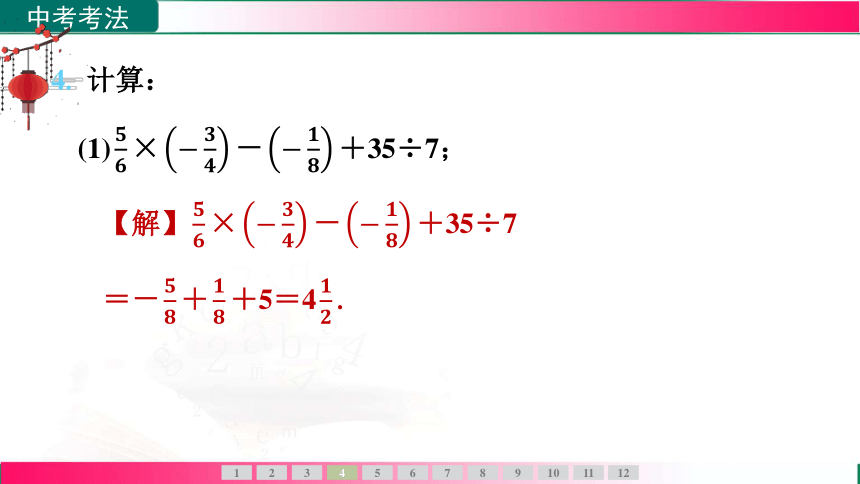
4. 计算:
(1) × - +35÷7;
【解】 × - +35÷7
=- + +5=4 .
1
2
3
4
5
6
7
8
9
10
11
12
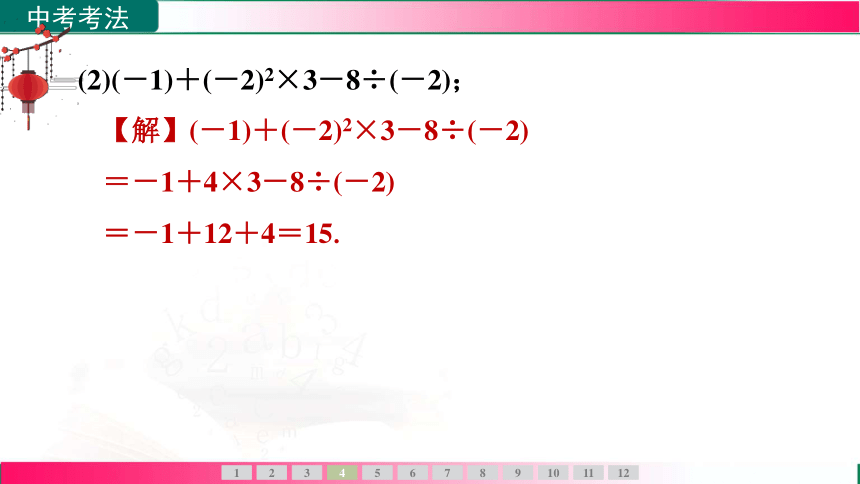
(2)(-1)+(-2)2×3-8÷(-2);
【解】(-1)+(-2)2×3-8÷(-2)
=-1+4×3-8÷(-2)
=-1+12+4=15.
1
2
3
4
5
6
7
8
9
10
11
12
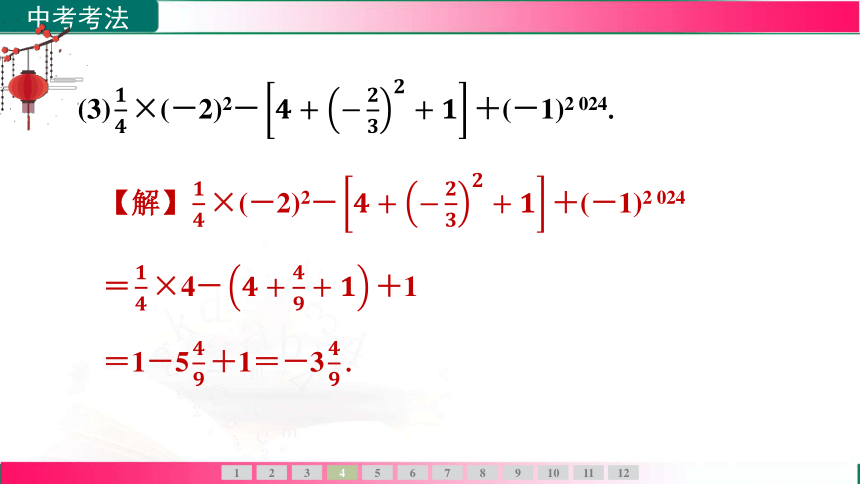
(3) ×(-2)2- +(-1)2 024.
【解】 ×(-2)2- +(-1)2 024
= ×4- +1
=1-5 +1=-3 .
1
2
3
4
5
6
7
8
9
10
11
12
有理数混合运算的应用
5. 某地区高度每增加100米,气温降低0.9 ℃,昊恩和美琪
两名同学想出一个测量山峰高度的办法,美琪在山脚,昊
恩跑到山顶,他们在同一时刻测得山脚的温度是3.8 ℃,
山顶的温度是-1.6 ℃,求山峰的高度.
1
2
3
4
5
6
7
8
9
10
11
12
【解】[3.8-(-1.6)]÷0.9×100
=(3.8+1.6)÷0.9×100
=5.4÷0.9×100
=600(米).
所以山峰的高度为600米.
1
2
3
4
5
6
7
8
9
10
11
12
6. 已知一个棱长为8 cm的立方体铁块.
(1)如图,把铁块放入装满水的圆柱形杯子中(杯子的底面
直径和高度均为20 cm),则溢出水的体积
为 cm3(溢出水的体积=铁块的体积);
512
1
2
3
4
5
6
7
8
9
10
11
12
(2)将铁块恰好分割成16个棱长为2 cm的立方体与6个棱长
为a cm的立方体,求a的值.
【解】棱长为a cm的立方体的体积为(512-16×23)÷6
=64(cm3).
因为43=64,所以a=4.
1
2
3
4
5
6
7
8
9
10
11
12
7. [新考向·传统文化]我国古代《易经》一书中记载,远古时
期,人们通过在绳子上打结来记录数量,即“结绳计
数”.如图,一位母亲在从右到左依次排列的绳子上打
结,满七进一,用来记录孩子自出生后的天数,由图可
知,孩子自出生后的天数是( C )
C
A. 84
B. 336
C. 167
D. 326
1
2
3
4
5
6
7
8
9
10
11
12
8. [2024·温州鹿城区月考]若计算式子(2□7)△ 的结果
为最大,则应分别在□,△中填入下列选项中的( D )
A. +,- B. ×,-
C. ÷,- D. -,÷
D
1
2
3
4
5
6
7
8
9
10
11
12
9. [2024·杭州西湖区期中]小明编制了一个计算机计算程序如
图所示,如果输入的数是5,则输出的数是 .
6
1
2
3
4
5
6
7
8
9
10
11
12
10. [新视角·新定义题]规定一种新的运算:a★b=ab-a
-b2+1.例如:3★(-4)=3×(-4)-3-(-4)2+1=
-30,请用上述规定计算下面各式:
(1)2★8;
【解】2★8=2×8-2-82+1=16-2-64+1=-49.
1
2
3
4
5
6
7
8
9
10
11
12
(2)(-7)★[5★(-2)].
【解】因为5★(-2)=5×(-2)-5-(-2)2+1=-10
-5-4+1=-18,
所以(-7)★[5★(-2)]=(-7)★(-18)=(-7)×(-18)
-(-7)-(-18)2+1=126+7-324+1=-190.
【解】因为5★(-2)=5×(-2)-5-(-2)2+1=-10
-5-4+1=-18,
所以(-7)★
=(-7)★(-18)=(-7)×(-18)
-(-7)-(-18)2+1=126+7-324+1=-190.
1
2
3
4
5
6
7
8
9
10
11
12
11. [母题 教材P66作业题T6]有一种“24”点游戏,其游戏
规则是:任取一副扑克牌,去掉大小王,我们约定A为
1,J,Q,K分别为11,12,13,并规定方块、红桃牌
为正,黑桃、梅花牌为负.任取4张牌将这4张牌的牌面所
表示的数进行加、减、乘、除、乘方运算(可使用括号).
每个数用且只用一次,使其结果等于24.
如:抽出4张牌分别为黑桃4、梅花2、方块4、红桃3,可
做运算:(-4)÷(-2)×4×3=24.
1
2
3
4
5
6
7
8
9
10
11
12
(1)若抽出黑桃3、梅花1、方块5、红桃3,请写出1种算
式,并写出计算过程,验证结果为24;
【解】答案不唯一,如
(-3)×(-1)×(5+3)
=(-3)×(-1)×8
=24.
(2)若抽出黑桃3、梅花K、方块8、红桃Q,请写出2种
不同的算式,并写出计算过程,验证结果为24;
1
2
3
4
5
6
7
8
9
10
11
12
【解】答案不唯一,如
①(-3)×8×(-13+12)
=(-3)×8×(-1)
=24;
②12×[(-3)-(-13)-8]
=12×2
=24.
1
2
3
4
5
6
7
8
9
10
11
12
(3)若抽出黑桃4、梅花7、方块2、红桃3,请设计1种含
“乘方”的混合运算的算式,并写出计算过程,验证
结果为24.
【解】答案不唯一,如
[(-4)-(-7)]×23
=3×8
=24.
1
2
3
4
5
6
7
8
9
10
11
12
12. [新视角·新定义题]类比乘方运算,我们规定:求n个相
同有理数(均不为0)的商的运算叫作除方.例如
2÷2÷2÷2,记作2“4”,读作“2的引4次商”;一般
地,把 (a≠0,n≥2,且为整数)记
作a“n”,读作“a的引n次商”.
1
2
3
4
5
6
7
8
9
10
11
12
(1)直接写出计算结果: = ,(-3)“5”
= ;
(2)归纳:负数的引正奇数次商是 数,负数的引正
偶数次商是 数(填“正”或“负”);
4
-
负
正
1
2
3
4
5
6
7
8
9
10
11
12
(3)计算:(-16)÷2“3”+12× .
【解】(-16)÷2“3”+12×
=(-16)÷ +12×9
=(-32)+108
=76.
1
2
3
4
5
6
7
8
9
10
11
12
谢谢观看!
2.6 有理数的混合运算
第2章 有理数的运算
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
有理数的混合运算
课程目标
掌握有理数混合运算的顺序,能正确进行包含加、减、乘、除、乘方的混合运算。
学会运用运算律简化有理数混合运算,提高运算的准确性和效率。
能够解决与有理数混合运算相关的实际问题,培养数学应用意识。
有理数混合运算的顺序
有理数混合运算的顺序是进行混合运算的核心依据,具体如下:
先算乘方:即先计算各个数的乘方运算,这是运算顺序的第一步。
再算乘除:在完成乘方运算后,按照从左到右的顺序依次进行乘法和除法运算。
最后算加减:乘除运算完成后,再按照从左到右的顺序进行加法和减法运算。
括号优先:如果式子中有括号,要先算括号里面的。括号分为小括号()、中括号 []、大括号 {},计算时要按照从小括号到中括号再到大括号的顺序依次进行。
实例说明
计算\(3 + 2^2\times( - 3)\):
先算乘方:\(2^2=4\)。
再算乘法:\(4\times( - 3)=-12\)。
最后算加法:\(3+( - 12)=-9\)。
计算\(18\div(3 - 6)\times2\):
先算小括号里的:\(3 - 6=-3\)。
再算除法:\(18\div( - 3)=-6\)。
最后算乘法:\(-6\times2=-12\)。
计算\([( - 2)^3 + 5]\div( - 3)\):
先算小括号里的乘方:\(( - 2)^3=-8\)。
再算小括号里的加法:\(-8 + 5=-3\)。
最后算中括号外的除法:\(-3\div( - 3)=1\)。
运算律在混合运算中的应用
在有理数混合运算中,合理运用加法交换律、结合律,乘法交换律、结合律和分配律,能有效简化运算过程。
加法运算律:在只有加减的运算中,可交换加数的位置或结合某些加数,使计算简便。例如,计算\(5+( - 3)+( - 5)+2\),利用加法交换律和结合律可得\([5+( - 5)]+[( - 3)+2]=0+( - 1)=-1\)。
乘法运算律:在乘除混合运算中,可交换因数的位置或结合某些因数。例如,计算\(( - 8)\times5\times( - 0.125)\times( - 2)\),利用乘法交换律和结合律可得\([( - 8)\times( - 0.125)]\times[5\times( - 2)]=1\times( - 10)=-10\)。
乘法分配律:当式子中出现一个数与多个数的和或差相乘时,使用分配律可简化运算。例如,计算\( - 24\times(\frac{1}{3}-\frac{1}{4}+\frac{1}{6})\),利用分配律可得\(-24\times\frac{1}{3}+24\times\frac{1}{4}-24\times\frac{1}{6}=-8 + 6-4=-6\)。
混合运算的易错点
运算顺序错误:忽略乘方、乘除、加减的优先级,或不遵循括号优先原则。例如,计算\(2 + 3\times4\)时,错误地先算加法再算乘法,得到\(5\times4=20\),而正确结果应为\(2 + 12=14\)。
符号错误:在涉及负数的运算中,容易弄错符号。例如,计算\(( - 2)^2\)时,错误地认为结果是\(-4\),而正确结果是\(4\);计算\(-2^2\)时,错误地认为结果是\(4\),而正确结果是\(-4\)。
漏算或重复计算:在步骤较多的运算中,容易漏算某些项或重复计算。例如,计算\(3\times(2 + 5)-4\)时,漏算减法得到\(3\times7=21\),而正确结果是\(21-4=17\)。
混合运算的简化技巧
观察式子结构:在动笔计算前,先观察式子的结构,判断是否能运用运算律简化运算。例如,式子\(100\times3.6 + 100\times6.4\)中,两项都有因数 100,可利用乘法分配律的逆运算简化为\(100\times(3.6 + 6.4)=100\times10=1000\)。
分步计算:对于复杂的混合运算,可分步进行计算,每一步只处理一种运算,减少错误。例如,计算\(10-( - 2)^3\div4\times( - 3)^2\),可先算乘方得到\(10-( - 8)\div4\times9\),再算除法得到\(10 - ( - 2)\times9\),接着算乘法得到\(10 + 18\),最后算加法得到\(28\)。
处理括号:当括号前是 “\(+\)” 号时,去掉括号后,括号内的各项符号不变;当括号前是 “\(-\)” 号时,去掉括号后,括号内的各项符号都要改变。例如,\(5-(3 - 2)=5 - 3 + 2=4\)。
实际应用举例
购物消费问题:小明去超市购物,买了 3 支单价为 5 元的钢笔,2 瓶单价为\(-3\)元的打折饮料(负号表示优惠),又买了一个价格为\(2^3\)元的笔记本,小明一共花了多少钱?
先分别计算各项费用:钢笔总价为\(3\times5 = 15\)元,饮料总价为\(2\times( - 3)=-6\)元,笔记本价格为\(2^3=8\)元。
再计算总花费:\(15+( - 6)+8=17\)元,即小明一共花了 17 元。
工程进度问题:一个工程队第一天完成了总工程的\(\frac{1}{4}\),第二天完成了总工程的\(\frac{1}{3}\),第三天比前两天的总和少完成总工程的\(\frac{1}{6}\),第三天完成了总工程的几分之几?
先算前两天完成的总和:\(\frac{1}{4}+\frac{1}{3}=\frac{3}{12}+\frac{4}{12}=\frac{7}{12}\)。
再算第三天完成的量:\(\frac{7}{12}-\frac{1}{6}=\frac{7}{12}-\frac{2}{12}=\frac{5}{12}\),即第三天完成了总工程的\(\frac{5}{12}\)。
课堂练习
计算下列各题:
\(10-( - 2)^2\times3\)
\(18\div(3 - 6)\times( - 2)\)
\([( - 1)^5 + 2]\times( - 4)\)
运用运算律简化计算:
\(25\times(4 - 0.4)\)
\( - 12\times\frac{1}{3}+12\times\frac{1}{4}-12\times\frac{1}{6}\)
总结
有理数混合运算的顺序是 “先乘方,再乘除,最后加减;有括号的先算括号里的”,必须严格遵循。
合理运用运算律能简化运算,提高效率,但要注意运算符号的变化。
实际应用中,需将问题转化为数学式子,再按照混合运算顺序求解,同时要注意单位和实际意义。
运算时要细心,避免因运算顺序错误、符号错误等导致结果出错,可通过分步计算和检查减少错误。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.掌握有理数混合运算的法则,会进行简单的有理数的混合
运算。
2.能合理地运用运算律简化运算,发展运算能力。
3.会利用有理数的混合运算解决简单实际问题。
一般地,有理数混合运算的法则是:
先算乘方,再算乘除,最后算加减。如有括号,先进行括号里
的运算。
若属于同级运算,则按照从左往右的顺序进行计算。
进行混合运算时,可以灵活运用运算律,但应注意符
号的确定以及运算顺序和方法的选择.例如,可以根据算式的
结构特征,巧用整体思想、拆分消除等技巧,从而使运算准
确、快捷。
知识过关
一般地,计算有理数混合运算时,先算 乘方 ,再
算 乘除 ,最后算 加减 .如有括号,先进行 括号
里的运算.
乘方
乘除
加减
括号
有理数的混合运算
1. 下列四个式子中,计算结果最小的是( D )
A. (-3-2)2 B. (-3)×(-2)2
C. -32÷(-2)2 D. -23-32
D
1
2
3
4
5
6
7
8
9
10
11
12
2. 下列各式计算正确的是( C )
C. 3×22-2×32=2×3×(2-3)=-6
D. (-42×32)=(-4×3)2=144
C
1
2
3
4
5
6
7
8
9
10
11
12
3. [2024·温州鹿城区期中]如图是一个计算程序,若输入a的
值为-1,则输出的结果b为 .
-5
1
2
3
4
5
6
7
8
9
10
11
12
4. 计算:
(1) × - +35÷7;
【解】 × - +35÷7
=- + +5=4 .
1
2
3
4
5
6
7
8
9
10
11
12
(2)(-1)+(-2)2×3-8÷(-2);
【解】(-1)+(-2)2×3-8÷(-2)
=-1+4×3-8÷(-2)
=-1+12+4=15.
1
2
3
4
5
6
7
8
9
10
11
12
(3) ×(-2)2- +(-1)2 024.
【解】 ×(-2)2- +(-1)2 024
= ×4- +1
=1-5 +1=-3 .
1
2
3
4
5
6
7
8
9
10
11
12
有理数混合运算的应用
5. 某地区高度每增加100米,气温降低0.9 ℃,昊恩和美琪
两名同学想出一个测量山峰高度的办法,美琪在山脚,昊
恩跑到山顶,他们在同一时刻测得山脚的温度是3.8 ℃,
山顶的温度是-1.6 ℃,求山峰的高度.
1
2
3
4
5
6
7
8
9
10
11
12
【解】[3.8-(-1.6)]÷0.9×100
=(3.8+1.6)÷0.9×100
=5.4÷0.9×100
=600(米).
所以山峰的高度为600米.
1
2
3
4
5
6
7
8
9
10
11
12
6. 已知一个棱长为8 cm的立方体铁块.
(1)如图,把铁块放入装满水的圆柱形杯子中(杯子的底面
直径和高度均为20 cm),则溢出水的体积
为 cm3(溢出水的体积=铁块的体积);
512
1
2
3
4
5
6
7
8
9
10
11
12
(2)将铁块恰好分割成16个棱长为2 cm的立方体与6个棱长
为a cm的立方体,求a的值.
【解】棱长为a cm的立方体的体积为(512-16×23)÷6
=64(cm3).
因为43=64,所以a=4.
1
2
3
4
5
6
7
8
9
10
11
12
7. [新考向·传统文化]我国古代《易经》一书中记载,远古时
期,人们通过在绳子上打结来记录数量,即“结绳计
数”.如图,一位母亲在从右到左依次排列的绳子上打
结,满七进一,用来记录孩子自出生后的天数,由图可
知,孩子自出生后的天数是( C )
C
A. 84
B. 336
C. 167
D. 326
1
2
3
4
5
6
7
8
9
10
11
12
8. [2024·温州鹿城区月考]若计算式子(2□7)△ 的结果
为最大,则应分别在□,△中填入下列选项中的( D )
A. +,- B. ×,-
C. ÷,- D. -,÷
D
1
2
3
4
5
6
7
8
9
10
11
12
9. [2024·杭州西湖区期中]小明编制了一个计算机计算程序如
图所示,如果输入的数是5,则输出的数是 .
6
1
2
3
4
5
6
7
8
9
10
11
12
10. [新视角·新定义题]规定一种新的运算:a★b=ab-a
-b2+1.例如:3★(-4)=3×(-4)-3-(-4)2+1=
-30,请用上述规定计算下面各式:
(1)2★8;
【解】2★8=2×8-2-82+1=16-2-64+1=-49.
1
2
3
4
5
6
7
8
9
10
11
12
(2)(-7)★[5★(-2)].
【解】因为5★(-2)=5×(-2)-5-(-2)2+1=-10
-5-4+1=-18,
所以(-7)★[5★(-2)]=(-7)★(-18)=(-7)×(-18)
-(-7)-(-18)2+1=126+7-324+1=-190.
【解】因为5★(-2)=5×(-2)-5-(-2)2+1=-10
-5-4+1=-18,
所以(-7)★
=(-7)★(-18)=(-7)×(-18)
-(-7)-(-18)2+1=126+7-324+1=-190.
1
2
3
4
5
6
7
8
9
10
11
12
11. [母题 教材P66作业题T6]有一种“24”点游戏,其游戏
规则是:任取一副扑克牌,去掉大小王,我们约定A为
1,J,Q,K分别为11,12,13,并规定方块、红桃牌
为正,黑桃、梅花牌为负.任取4张牌将这4张牌的牌面所
表示的数进行加、减、乘、除、乘方运算(可使用括号).
每个数用且只用一次,使其结果等于24.
如:抽出4张牌分别为黑桃4、梅花2、方块4、红桃3,可
做运算:(-4)÷(-2)×4×3=24.
1
2
3
4
5
6
7
8
9
10
11
12
(1)若抽出黑桃3、梅花1、方块5、红桃3,请写出1种算
式,并写出计算过程,验证结果为24;
【解】答案不唯一,如
(-3)×(-1)×(5+3)
=(-3)×(-1)×8
=24.
(2)若抽出黑桃3、梅花K、方块8、红桃Q,请写出2种
不同的算式,并写出计算过程,验证结果为24;
1
2
3
4
5
6
7
8
9
10
11
12
【解】答案不唯一,如
①(-3)×8×(-13+12)
=(-3)×8×(-1)
=24;
②12×[(-3)-(-13)-8]
=12×2
=24.
1
2
3
4
5
6
7
8
9
10
11
12
(3)若抽出黑桃4、梅花7、方块2、红桃3,请设计1种含
“乘方”的混合运算的算式,并写出计算过程,验证
结果为24.
【解】答案不唯一,如
[(-4)-(-7)]×23
=3×8
=24.
1
2
3
4
5
6
7
8
9
10
11
12
12. [新视角·新定义题]类比乘方运算,我们规定:求n个相
同有理数(均不为0)的商的运算叫作除方.例如
2÷2÷2÷2,记作2“4”,读作“2的引4次商”;一般
地,把 (a≠0,n≥2,且为整数)记
作a“n”,读作“a的引n次商”.
1
2
3
4
5
6
7
8
9
10
11
12
(1)直接写出计算结果: = ,(-3)“5”
= ;
(2)归纳:负数的引正奇数次商是 数,负数的引正
偶数次商是 数(填“正”或“负”);
4
-
负
正
1
2
3
4
5
6
7
8
9
10
11
12
(3)计算:(-16)÷2“3”+12× .
【解】(-16)÷2“3”+12×
=(-16)÷ +12×9
=(-32)+108
=76.
1
2
3
4
5
6
7
8
9
10
11
12
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
