3.3 立方根 课件(共36张PPT)
图片预览









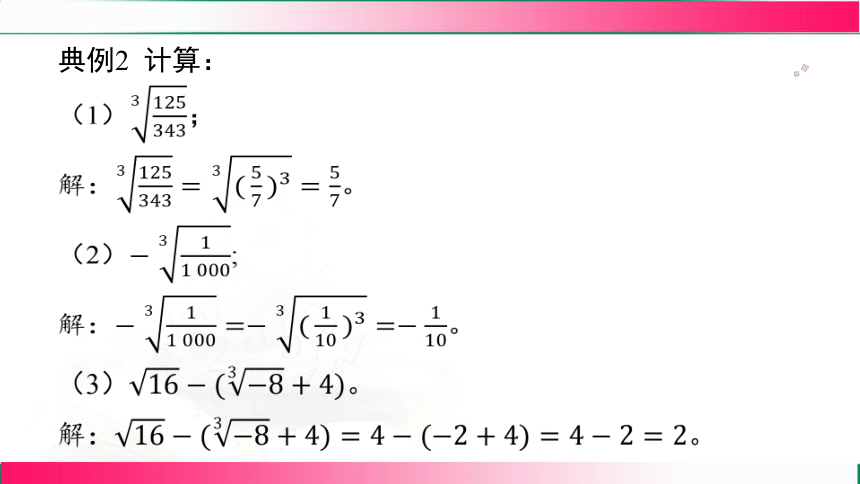
文档简介
(共36张PPT)
3.3 立方根
第3章 实数
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
立方根
课程目标
理解立方根的概念,掌握立方根的表示方法。
掌握立方根的性质,能熟练求出一个数的立方根。
了解开立方运算的意义,明确立方根与平方根的区别和联系。
学会运用立方根解决实际问题。
立方根的定义
如果一个数的立方等于\(a\),那么这个数叫做\(a\)的立方根(也叫做三次方根)。也就是说,如果\(x^3 = a\),那么\(x\)叫做\(a\)的立方根。
例如,因为\(2^3 = 8\),所以 2 是 8 的立方根;因为\((-2)^3=-8\),所以 - 2 是 - 8 的立方根;因为\(0^3 = 0\),所以 0 是 0 的立方根。
立方根的表示方法
一个数\(a\)的立方根记为\(\sqrt[3]{a}\),读作 “三次根号\(a\)”,其中\(a\)叫做被开方数,3 叫做根指数。
注意:根指数 3 不能省略,这是与平方根的表示方法的重要区别(平方根的根指数 2 通常省略)。例如,8 的立方根表示为\(\sqrt[3]{8}\),-27 的立方根表示为\(\sqrt[3]{-27}\)。
立方根的性质
正数的立方根是正数:例如,\(8\)是正数,它的立方根\(\sqrt[3]{8}=2\)也是正数。
负数的立方根是负数:例如,\(-8\)是负数,它的立方根\(\sqrt[3]{-8}=-2\)也是负数。
0 的立方根是 0:即\(\sqrt[3]{0}=0\)。
唯一性:每个数都有且只有一个立方根,这与平方根不同(正数有两个平方根)。
开立方运算
求一个数的立方根的运算,叫做开立方。开立方与立方互为逆运算,我们可以利用这种逆运算关系来求一个数的立方根。
例如,因为\(5^3 = 125\),所以\(\sqrt[3]{125}=5\)(开立方是立方的逆运算);因为\((-0.3)^3=-0.027\),所以\(\sqrt[3]{-0.027}=-0.3\)。
求立方根的方法
根据定义求解:找到一个数,使得它的立方等于被开方数。例如,求\(\sqrt[3]{27}\),因为\(3^3 = 27\),所以\(\sqrt[3]{27}=3\)。
利用立方与开立方的互逆关系:通过立方运算来检验所求的立方根是否正确。例如,要验证\(\sqrt[3]{-64}=-4\),只需计算\((-4)^3=-64\),与被开方数相等,说明结果正确。
对于小数或分数的立方根:可以将其化为整数或最简分数的形式,再进行求解。例如,求\(\sqrt[3]{0.125}\),因为\(0.5^3 = 0.125\),所以\(\sqrt[3]{0.125}=0.5\);求\(\sqrt[3]{\frac{8}{27}}\),因为\((\frac{2}{3})^3=\frac{8}{27}\),所以\(\sqrt[3]{\frac{8}{27}}=\frac{2}{3}\)。
立方根与平方根的区别和联系
区别
定义不同:立方根是如果\(x^3 = a\),那么\(x\)叫做\(a\)的立方根;平方根是如果\(x^2 = a\)(\(a\geq0\)),那么\(x\)叫做\(a\)的平方根。
表示方法不同:立方根表示为\(\sqrt[3]{a}\),根指数 3 不能省略;平方根表示为\(\pm\sqrt{a}\)(\(a\geq0\)),根指数 2 通常省略。
性质不同:正数的立方根是正数,负数的立方根是负数,0 的立方根是 0,每个数都有且只有一个立方根;正数有两个互为相反数的平方根,0 的平方根是 0,负数没有平方根。
被开方数的取值范围不同:立方根的被开方数可以是任意实数;平方根的被开方数必须是非负数(\(a\geq0\))。
联系
开方运算不同:开立方与立方互为逆运算,开平方与平方互为逆运算。
运算结果的表示:都用根号表示运算结果。
立方根的应用
几何问题:在求正方体的棱长时,若已知正方体的体积,可通过求体积的立方根得到棱长。例如,一个正方体的体积是 125 立方厘米,它的棱长是\(\sqrt[3]{125}=5\)厘米。
物理问题:在计算物体的密度时,密度公式为\(\rho=\frac{m}{V}\)(其中\(\rho\)为密度,\(m\)为质量,\(V\)为体积),若已知质量和密度,求体积\(V=\frac{m}{\rho}\),当体积涉及开立方时,就需要用到立方根。例如,已知某物体的质量为 216 克,密度为 1 克 / 立方厘米,可得体积\(V = 216\)立方厘米,该正方体物体的棱长为\(\sqrt[3]{216}=6\)厘米。
实际测量:在测量一些不规则物体的体积时,有时需要通过计算立方根来得到相关的长度数据。例如,一个球体的体积是\(\frac{4}{3}\pi\)立方分米,根据球体体积公式\(V=\frac{4}{3}\pi r^3\)(其中\(r\)为半径),可得\(r^3 = 1\),则半径\(r=\sqrt[3]{1}=1\)分米。
课堂练习
求下列各数的立方根:
64
-125
0.008
\(\frac{27}{64}\)
0
判断下列说法是否正确:
64 的立方根是 4。
-8 没有立方根。
0 的立方根是 0。
立方根等于它本身的数只有 0。
若一个数的立方根是 - 3,求这个数。
总结
立方根的定义是如果\(x^3 = a\),那么\(x\)叫做\(a\)的立方根,记为\(\sqrt[3]{a}\)。
正数的立方根是正数,负数的立方根是负数,0 的立方根是 0,每个数都有唯一的立方根。
开立方与立方互为逆运算,求立方根可根据定义和这种逆运算关系。
立方根与平方根在定义、表示方法、性质等方面有区别也有联系,在几何、物理等领域有重要应用。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.了解立方根的概念,会用根号表示数的立方根。
2.理解立方根的事实。
3.了解开立方与立方互为逆运算,会用立方运算求完全立方数
的立方根(及对应的负整数),发展运算能力。
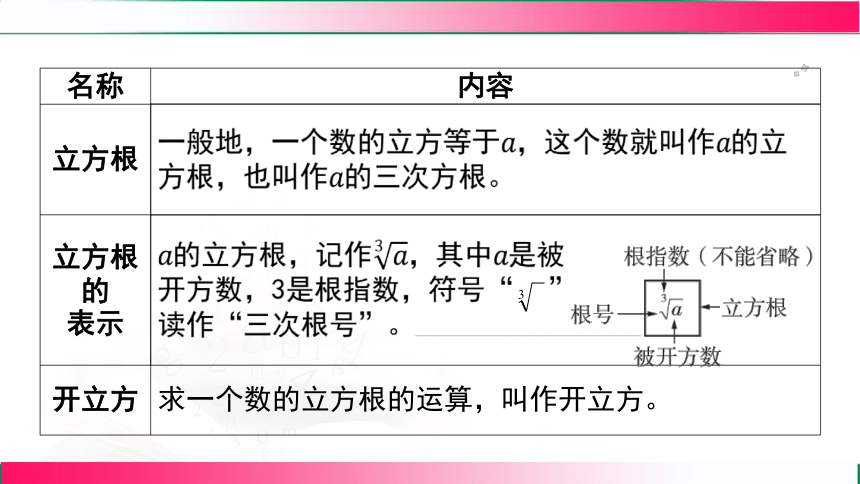
名称 内容
立方根
立方根的 表示
开立方 求一个数的立方根的运算,叫作开立方。
(1) 中的根指数3不能省略,要写在根号的左上角;
(2)开立方与立方是互逆的运算,所以可以运用立方运算求
一个数的立方根;
(3)开立方时,被开方数可以是任意实数,且立方根的符号
与被开方数的符号相同。
典例1 求下列各数的立方根:
(1)343;
解:因为,所以343的立方根为7,即 。
(2) ;
解:因为, ,
所以的立方根为,即 。
(3) 。
解:因为,,
所以的立方根为 ,
即 。
1.立方根的事实:一个正数有一个正的立方根;一个负数有
一个负的立方根;零的立方根是零。
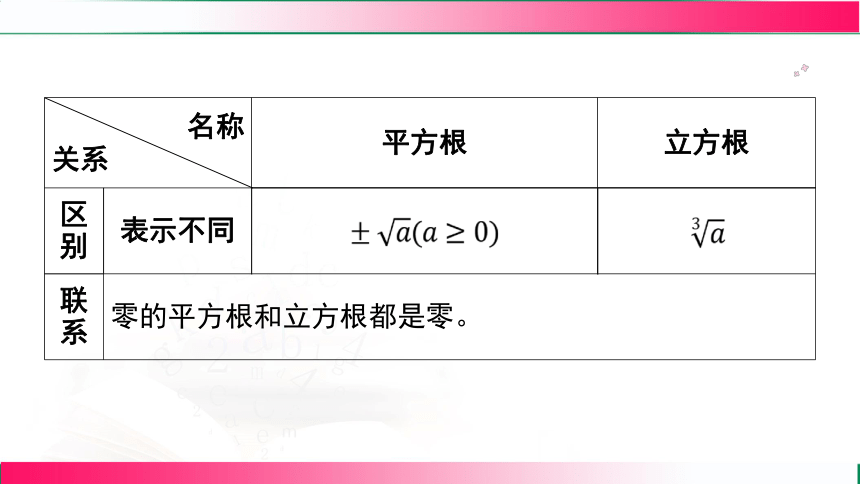
2.平方根与立方根的区别与联系
名称 关系 平方根 立方根
区别 被开方数 的取值范 围不同
名称 关系 平方根 立方根 区别 特征不同 正数有两个平方根,它们互为相反数。 只有非负数才有平方根。 正数的立方根是正数。 负数也
有立方
根。
负数没有平方根。 负数的立方根是负数。 名称 关系 平方根 立方根
区别 表示不同
联系 零的平方根和立方根都是零。
敲黑板
(1)互为相反数的两个数,它们的立方根也互为相反数,即
。利用“ ”可以把求一个负数的立方
根转化为求一个正数的立方根的相反数。例如,
。
(2),。例如,,
。
典例2 计算:
(1) ;
解: 。
(2) ;
解: 。
(3) 。
解: 。
知识过关
①一般地,一个数的立方等于a,这个数就叫作a的 立方
根 ,也叫作a的 三次方根 ,记作 .
②一个正数有一个 正 的立方根;一个负数有一个 负 的立方根;0的立方根是 0 .
立方
根
三次方根
正
负
0
立方根的概念及计算
1.64的立方根是( B )
A. ±4 B. 4
C. -4 D. 不存在
2. [2024·温州龙湾区一模]下列各数中,立方根不等于它本身
的是( B )
A. 1 B. 2 C. 0 D. -1
B
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
3. [母题 教材P90作业题T1]下列说法不正确的是( B )
A. 2是8的立方根
B. ±5是125的立方根
D. (-4)3的立方根是-4
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
4. 体积为16的正方体,其棱长等于( C )
A. 16的平方根 B. 16的算术平方根
C. 16的立方根 D. 4的算术平方根
C
5. 的立方根是 .
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
6. [母题 教材P88例1]求下列各数的立方根:
(1)125;
【解】因为53=125,
所以125的立方根是5,即 =5.
因为(-0.6)3=-0.216,所以-0.216的立方根是-0.6,即 =-0.6.
(2)-0.216;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(3)- ;
因为 =- ,
所以- 的立方根是- ,即 =- .
因为(-10)3=-1 000,所以-1 000的立方根是-10,即 =-10.
(4)-1 000;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
因为15 = , = ,
所以15 的立方根为 ,即 = .
(5)15 .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
7. 分别求下列各式的值:
(1) ;
(2) ;
【解】原式=9.
【解】原式=0.1.
(3) ;
(4)- .
【解】原式=- .
【解】原式= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
立方根的性质
8. 下列结论正确的是( D )
A. 216的立方根是±6
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
9. 下列说法正确的是( D )
A. 负数没有立方根
B. 如果一个数有立方根,那么它一定有平方根
C. 一个数的立方根有两个,它们互为相反数
D. 一个数的立方根与被开方数同号
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
10. [2024·杭州西湖区期中]若a+b=0,a≠0,则 与
的关系是( B )
A. 相等 B. 互为相反数
C. 互为倒数 D. 相等或互为相反数
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[易错题]对立方根与平方根的性质理解不透彻而出错
11. 下列正确的有( B )
①只有正数才有平方根;②a一定有立方根;③ 没
意义;④ =- ;⑤只有正数才有立方根.
A. 1个 B. 2个
C. 3个 D. 4个
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
12. 估计68的立方根的大小在( C )
A. 2与3之间 B. 3与4之间
C. 4与5之间 D. 5与6之间
【点拨】
因为43=64,53=125,64<68<125,所以4<
<5.
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
13. a是(-8)2的平方根,则a的立方根是( C )
A. -8 B. 2
C. 2或-2 D. 8或-8
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
14. 计算:
(1) + - = ;
(2) - + = .
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
15. [2024·绍兴期中]已知一个立方体的体积是1 000 cm3,现
在要在它的8个角上分别截去1个大小相同的小立方体,
截去后余下部分的体积为488 cm3,则截去的每个小立方
体的棱长是 cm.
16. 正整数a,b分别满足 <a< , <b<
,则a+b= .
4
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
【解】因为2a-1的平方根是±3,
所以2a-1=9,所以a=5.
因为3a+b-1的算术平方根是4,
所以3a+b-1=16,所以b=2.
所以50a-17b=250-34=216.
因为216的立方根为6,所以50a-17b的立方根为6.
17. 已知2a-1的平方根是±3,3a+b-1的算术平方根是
4,求50a-17b的立方根.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
18. [母题 教材P90作业题T6]如图,这是由8个同样大小的立
方体组成的魔方,体积为216 cm3.
(1)求出这个魔方的棱长;
【解】 =6(cm),
所以这个魔方的棱长是6 cm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(2)图中阴影部分是一个正方形,求出阴影部分的面积及
其边长.
【解】因为魔方的棱长为6 cm,
所以小立方体的棱长为6÷2=3(cm),
所以阴影部分的面积为 ×3×3×4=
18(cm2),边长为 cm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
19. [母题 教材P90探究活动]类比平方根(二次方根)、立方根
(三次方根)的定义可给出四次方根、五次方根的定义:
①如果x4=a(a≥0),那么x叫作a的四次方根;
②如果x5=a,那么x叫作a的五次方根.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
请根据以上两个定义并结合有关数学知识回答问题:
(1)81的四次方根为 ;-32的五次方根为 .
(2)若 有意义,则a的取值范围为 ;若
有意义,则a的取值范围为 .
±3
-
2
a≥1
全体实数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(3)解方程:
①x4=16; ②100 000x5=243.
【解】①因为x4=16, =16,
所以x=±2.
②因为100 000x5=243,所以x5= ,
因为 = ,所以x= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
谢谢观看!
3.3 立方根
第3章 实数
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
立方根
课程目标
理解立方根的概念,掌握立方根的表示方法。
掌握立方根的性质,能熟练求出一个数的立方根。
了解开立方运算的意义,明确立方根与平方根的区别和联系。
学会运用立方根解决实际问题。
立方根的定义
如果一个数的立方等于\(a\),那么这个数叫做\(a\)的立方根(也叫做三次方根)。也就是说,如果\(x^3 = a\),那么\(x\)叫做\(a\)的立方根。
例如,因为\(2^3 = 8\),所以 2 是 8 的立方根;因为\((-2)^3=-8\),所以 - 2 是 - 8 的立方根;因为\(0^3 = 0\),所以 0 是 0 的立方根。
立方根的表示方法
一个数\(a\)的立方根记为\(\sqrt[3]{a}\),读作 “三次根号\(a\)”,其中\(a\)叫做被开方数,3 叫做根指数。
注意:根指数 3 不能省略,这是与平方根的表示方法的重要区别(平方根的根指数 2 通常省略)。例如,8 的立方根表示为\(\sqrt[3]{8}\),-27 的立方根表示为\(\sqrt[3]{-27}\)。
立方根的性质
正数的立方根是正数:例如,\(8\)是正数,它的立方根\(\sqrt[3]{8}=2\)也是正数。
负数的立方根是负数:例如,\(-8\)是负数,它的立方根\(\sqrt[3]{-8}=-2\)也是负数。
0 的立方根是 0:即\(\sqrt[3]{0}=0\)。
唯一性:每个数都有且只有一个立方根,这与平方根不同(正数有两个平方根)。
开立方运算
求一个数的立方根的运算,叫做开立方。开立方与立方互为逆运算,我们可以利用这种逆运算关系来求一个数的立方根。
例如,因为\(5^3 = 125\),所以\(\sqrt[3]{125}=5\)(开立方是立方的逆运算);因为\((-0.3)^3=-0.027\),所以\(\sqrt[3]{-0.027}=-0.3\)。
求立方根的方法
根据定义求解:找到一个数,使得它的立方等于被开方数。例如,求\(\sqrt[3]{27}\),因为\(3^3 = 27\),所以\(\sqrt[3]{27}=3\)。
利用立方与开立方的互逆关系:通过立方运算来检验所求的立方根是否正确。例如,要验证\(\sqrt[3]{-64}=-4\),只需计算\((-4)^3=-64\),与被开方数相等,说明结果正确。
对于小数或分数的立方根:可以将其化为整数或最简分数的形式,再进行求解。例如,求\(\sqrt[3]{0.125}\),因为\(0.5^3 = 0.125\),所以\(\sqrt[3]{0.125}=0.5\);求\(\sqrt[3]{\frac{8}{27}}\),因为\((\frac{2}{3})^3=\frac{8}{27}\),所以\(\sqrt[3]{\frac{8}{27}}=\frac{2}{3}\)。
立方根与平方根的区别和联系
区别
定义不同:立方根是如果\(x^3 = a\),那么\(x\)叫做\(a\)的立方根;平方根是如果\(x^2 = a\)(\(a\geq0\)),那么\(x\)叫做\(a\)的平方根。
表示方法不同:立方根表示为\(\sqrt[3]{a}\),根指数 3 不能省略;平方根表示为\(\pm\sqrt{a}\)(\(a\geq0\)),根指数 2 通常省略。
性质不同:正数的立方根是正数,负数的立方根是负数,0 的立方根是 0,每个数都有且只有一个立方根;正数有两个互为相反数的平方根,0 的平方根是 0,负数没有平方根。
被开方数的取值范围不同:立方根的被开方数可以是任意实数;平方根的被开方数必须是非负数(\(a\geq0\))。
联系
开方运算不同:开立方与立方互为逆运算,开平方与平方互为逆运算。
运算结果的表示:都用根号表示运算结果。
立方根的应用
几何问题:在求正方体的棱长时,若已知正方体的体积,可通过求体积的立方根得到棱长。例如,一个正方体的体积是 125 立方厘米,它的棱长是\(\sqrt[3]{125}=5\)厘米。
物理问题:在计算物体的密度时,密度公式为\(\rho=\frac{m}{V}\)(其中\(\rho\)为密度,\(m\)为质量,\(V\)为体积),若已知质量和密度,求体积\(V=\frac{m}{\rho}\),当体积涉及开立方时,就需要用到立方根。例如,已知某物体的质量为 216 克,密度为 1 克 / 立方厘米,可得体积\(V = 216\)立方厘米,该正方体物体的棱长为\(\sqrt[3]{216}=6\)厘米。
实际测量:在测量一些不规则物体的体积时,有时需要通过计算立方根来得到相关的长度数据。例如,一个球体的体积是\(\frac{4}{3}\pi\)立方分米,根据球体体积公式\(V=\frac{4}{3}\pi r^3\)(其中\(r\)为半径),可得\(r^3 = 1\),则半径\(r=\sqrt[3]{1}=1\)分米。
课堂练习
求下列各数的立方根:
64
-125
0.008
\(\frac{27}{64}\)
0
判断下列说法是否正确:
64 的立方根是 4。
-8 没有立方根。
0 的立方根是 0。
立方根等于它本身的数只有 0。
若一个数的立方根是 - 3,求这个数。
总结
立方根的定义是如果\(x^3 = a\),那么\(x\)叫做\(a\)的立方根,记为\(\sqrt[3]{a}\)。
正数的立方根是正数,负数的立方根是负数,0 的立方根是 0,每个数都有唯一的立方根。
开立方与立方互为逆运算,求立方根可根据定义和这种逆运算关系。
立方根与平方根在定义、表示方法、性质等方面有区别也有联系,在几何、物理等领域有重要应用。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.了解立方根的概念,会用根号表示数的立方根。
2.理解立方根的事实。
3.了解开立方与立方互为逆运算,会用立方运算求完全立方数
的立方根(及对应的负整数),发展运算能力。
名称 内容
立方根
立方根的 表示
开立方 求一个数的立方根的运算,叫作开立方。
(1) 中的根指数3不能省略,要写在根号的左上角;
(2)开立方与立方是互逆的运算,所以可以运用立方运算求
一个数的立方根;
(3)开立方时,被开方数可以是任意实数,且立方根的符号
与被开方数的符号相同。
典例1 求下列各数的立方根:
(1)343;
解:因为,所以343的立方根为7,即 。
(2) ;
解:因为, ,
所以的立方根为,即 。
(3) 。
解:因为,,
所以的立方根为 ,
即 。
1.立方根的事实:一个正数有一个正的立方根;一个负数有
一个负的立方根;零的立方根是零。
2.平方根与立方根的区别与联系
名称 关系 平方根 立方根
区别 被开方数 的取值范 围不同
名称 关系 平方根 立方根 区别 特征不同 正数有两个平方根,它们互为相反数。 只有非负数才有平方根。 正数的立方根是正数。 负数也
有立方
根。
负数没有平方根。 负数的立方根是负数。 名称 关系 平方根 立方根
区别 表示不同
联系 零的平方根和立方根都是零。
敲黑板
(1)互为相反数的两个数,它们的立方根也互为相反数,即
。利用“ ”可以把求一个负数的立方
根转化为求一个正数的立方根的相反数。例如,
。
(2),。例如,,
。
典例2 计算:
(1) ;
解: 。
(2) ;
解: 。
(3) 。
解: 。
知识过关
①一般地,一个数的立方等于a,这个数就叫作a的 立方
根 ,也叫作a的 三次方根 ,记作 .
②一个正数有一个 正 的立方根;一个负数有一个 负 的立方根;0的立方根是 0 .
立方
根
三次方根
正
负
0
立方根的概念及计算
1.64的立方根是( B )
A. ±4 B. 4
C. -4 D. 不存在
2. [2024·温州龙湾区一模]下列各数中,立方根不等于它本身
的是( B )
A. 1 B. 2 C. 0 D. -1
B
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
3. [母题 教材P90作业题T1]下列说法不正确的是( B )
A. 2是8的立方根
B. ±5是125的立方根
D. (-4)3的立方根是-4
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
4. 体积为16的正方体,其棱长等于( C )
A. 16的平方根 B. 16的算术平方根
C. 16的立方根 D. 4的算术平方根
C
5. 的立方根是 .
2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
6. [母题 教材P88例1]求下列各数的立方根:
(1)125;
【解】因为53=125,
所以125的立方根是5,即 =5.
因为(-0.6)3=-0.216,所以-0.216的立方根是-0.6,即 =-0.6.
(2)-0.216;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(3)- ;
因为 =- ,
所以- 的立方根是- ,即 =- .
因为(-10)3=-1 000,所以-1 000的立方根是-10,即 =-10.
(4)-1 000;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
因为15 = , = ,
所以15 的立方根为 ,即 = .
(5)15 .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
7. 分别求下列各式的值:
(1) ;
(2) ;
【解】原式=9.
【解】原式=0.1.
(3) ;
(4)- .
【解】原式=- .
【解】原式= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
立方根的性质
8. 下列结论正确的是( D )
A. 216的立方根是±6
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
9. 下列说法正确的是( D )
A. 负数没有立方根
B. 如果一个数有立方根,那么它一定有平方根
C. 一个数的立方根有两个,它们互为相反数
D. 一个数的立方根与被开方数同号
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
10. [2024·杭州西湖区期中]若a+b=0,a≠0,则 与
的关系是( B )
A. 相等 B. 互为相反数
C. 互为倒数 D. 相等或互为相反数
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[易错题]对立方根与平方根的性质理解不透彻而出错
11. 下列正确的有( B )
①只有正数才有平方根;②a一定有立方根;③ 没
意义;④ =- ;⑤只有正数才有立方根.
A. 1个 B. 2个
C. 3个 D. 4个
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
12. 估计68的立方根的大小在( C )
A. 2与3之间 B. 3与4之间
C. 4与5之间 D. 5与6之间
【点拨】
因为43=64,53=125,64<68<125,所以4<
<5.
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
13. a是(-8)2的平方根,则a的立方根是( C )
A. -8 B. 2
C. 2或-2 D. 8或-8
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
14. 计算:
(1) + - = ;
(2) - + = .
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
15. [2024·绍兴期中]已知一个立方体的体积是1 000 cm3,现
在要在它的8个角上分别截去1个大小相同的小立方体,
截去后余下部分的体积为488 cm3,则截去的每个小立方
体的棱长是 cm.
16. 正整数a,b分别满足 <a< , <b<
,则a+b= .
4
6
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
【解】因为2a-1的平方根是±3,
所以2a-1=9,所以a=5.
因为3a+b-1的算术平方根是4,
所以3a+b-1=16,所以b=2.
所以50a-17b=250-34=216.
因为216的立方根为6,所以50a-17b的立方根为6.
17. 已知2a-1的平方根是±3,3a+b-1的算术平方根是
4,求50a-17b的立方根.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
18. [母题 教材P90作业题T6]如图,这是由8个同样大小的立
方体组成的魔方,体积为216 cm3.
(1)求出这个魔方的棱长;
【解】 =6(cm),
所以这个魔方的棱长是6 cm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(2)图中阴影部分是一个正方形,求出阴影部分的面积及
其边长.
【解】因为魔方的棱长为6 cm,
所以小立方体的棱长为6÷2=3(cm),
所以阴影部分的面积为 ×3×3×4=
18(cm2),边长为 cm.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
19. [母题 教材P90探究活动]类比平方根(二次方根)、立方根
(三次方根)的定义可给出四次方根、五次方根的定义:
①如果x4=a(a≥0),那么x叫作a的四次方根;
②如果x5=a,那么x叫作a的五次方根.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
请根据以上两个定义并结合有关数学知识回答问题:
(1)81的四次方根为 ;-32的五次方根为 .
(2)若 有意义,则a的取值范围为 ;若
有意义,则a的取值范围为 .
±3
-
2
a≥1
全体实数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
(3)解方程:
①x4=16; ②100 000x5=243.
【解】①因为x4=16, =16,
所以x=±2.
②因为100 000x5=243,所以x5= ,
因为 = ,所以x= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
