4.3 整式 课件（共37张PPT）

(共37张PPT)
4.3 整式
第4章 代数式
【2025-2026学年】浙教版 数学 七年级上册
授课教师：********
班 级：********
时 间：********
整式
课程目标
理解整式的概念，能区分整式与非整式。
掌握单项式和多项式的定义，明确它们的相关概念（系数、次数、项、常数项等）。
能够准确判断一个代数式是否为单项式或多项式，并指出其相关属性。
了解整式在实际生活中的应用。
整式的定义
单项式和多项式统称为整式。也就是说，整式是代数式的一部分，它不包含字母在分母中或根号下的形式。
例如：\(3x\)、\(a + b\)、\(5x^2y - 3xy + 1\)等都是整式；而\(\frac{1}{x}\)（字母在分母）、\(\sqrt{x}\)（字母在根号下）等不是整式。
单项式
定义
由数与字母的积组成的代数式叫做单项式，单独的一个数或一个字母也叫做单项式。
例如：\(5\)、\(a\)、\(3xy\)、\(-2x^2y^3\)等都是单项式。
相关概念
系数：单项式中的数字因数叫做这个单项式的系数。
例如：单项式\(3xy\)的系数是\(3\)；单项式\(-2x^2y^3\)的系数是\(-2\)；单项式\(a\)的系数是\(1\)（省略不写）；单项式\(-5\)的系数是\(-5\)。
次数：一个单项式中，所有字母的指数的和叫做这个单项式的次数。
例如：单项式\(3xy\)中\(x\)的指数是\(1\)，\(y\)的指数是\(1\)，次数是\(1 + 1=2\)；单项式\(-2x^2y^3\)中\(x\)的指数是\(2\)，\(y\)的指数是\(3\)，次数是\(2 + 3=5\)；单项式\(5\)是常数项，它的次数是\(0\)。
多项式
定义
几个单项式的和叫做多项式。
例如：\(x + y\)（\(x\)和\(y\)都是单项式，它们的和是多项式）、\(3x^2 - 2xy + 5\)（\(3x^2\)、\(-2xy\)、\(5\)都是单项式，它们的和是多项式）等都是多项式。
相关概念
项：在多项式中，每个单项式叫做多项式的项，其中不含字母的项叫做常数项。
例如：多项式\(3x^2 - 2xy + 5\)中，\(3x^2\)、\(-2xy\)、\(5\)都是它的项，其中\(5\)是常数项。
次数：多项式里次数最高项的次数，叫做这个多项式的次数。
例如：多项式\(3x^2 - 2xy + 5\)中，\(3x^2\)的次数是\(2\)，\(-2xy\)的次数是\(2\)，常数项\(5\)的次数是\(0\)，所以这个多项式的次数是\(2\)。
多项式的命名：一个多项式含有几项，就叫做几项式。例如，\(x + y\)含有\(2\)项，叫做二项式；\(3x^2 - 2xy + 5\)含有\(3\)项，叫做三项式。通常将多项式的项数和次数结合起来命名，如\(3x^2 - 2xy + 5\)是二次三项式。
单项式与多项式的区别和联系
区别
组成不同：单项式是数与字母的积，或单独的数、字母；多项式是几个单项式的和。
项数不同：单项式只有一项；多项式至少有两项。
联系
单项式和多项式统称为整式。
多项式是由单项式组成的，多项式中的每一项都是单项式。
实例解析
判断单项式及其相关属性
代数式\(5x^3y\)：是单项式，系数是\(5\)，因为\(x\)的指数是\(3\)，\(y\)的指数是\(1\)，所以次数是\(3 + 1=4\)。
代数式\(-a\)：是单项式，系数是\(-1\)，次数是\(1\)（只有字母\(a\)，指数是\(1\)）。
代数式\(8\)：是单项式，系数是\(8\)，次数是\(0\)。
判断多项式及其相关属性
代数式\(4x^2 - 3x + 7\)：是多项式，由\(4x^2\)、\(-3x\)、\(7\)三项组成，所以是三项式。其中最高次项是\(4x^2\)，次数是\(2\)，因此这个多项式是二次三项式，常数项是\(7\)。
代数式\(a^3b - 2ab^2 + b - 5\)：是多项式，含有\(4\)项，是四项式。\(a^3b\)的次数是\(4\)（\(3 + 1\)），\(-2ab^2\)的次数是\(3\)（\(1 + 2\)），\(b\)的次数是\(1\)，\(-5\)的次数是\(0\)，最高次项是\(a^3b\)，次数是\(4\)，所以这个多项式是四次四项式，常数项是\(-5\)。
整式的应用
几何问题：用整式表示图形的周长、面积、体积等。例如，一个长方形的长为\(a\)，宽为\(b\)，它的周长可以用整式\(2(a + b)\)表示，面积可以用整式\(ab\)表示；一个正方体的棱长为\(x\)，它的体积可以用整式\(x^3\)表示。
实际生活问题：用整式表示实际中的数量关系。例如，某水果的单价为每千克\(m\)元，买\(n\)千克需要花费\(mn\)元（单项式）；某书店卖书，一本故事书\(a\)元，一本科技书\(b\)元，买\(2\)本故事书和\(3\)本科技书一共需要\((2a + 3b)\)元（多项式）。
科学计算：在一些科学公式中，整式也有广泛应用。例如，物理学中匀速直线运动的路程公式\(s=vt\)（\(s\)表示路程，\(v\)表示速度，\(t\)表示时间），这是一个单项式；圆柱体的体积公式\(V=\pi r^2h\)（\(r\)表示底面半径，\(h\)表示高），也是一个单项式。
课堂练习
判断下列代数式是否为整式，若是整式，指出是单项式还是多项式，并说明其相关属性（系数、次数、项数等）：
\(3x^2y\)
\(\frac{1}{x} + 2\)
\(5a - 3b + 1\)
\(-7\)
\(x^3 - 2x^2 + x - 6\)
说出下列多项式是几次几项式，指出其常数项：
\(2x + 1\)
\(3x^2y - 2xy^2 + y^3 - 4\)
总结
整式包括单项式和多项式，它不包含字母在分母或根号下的形式。
单项式是数与字母的积或单独的数、字母，有系数和次数；多项式是几个单项式的和，有项、项数、次数、常数项等概念。
能准确区分单项式和多项式，并明确它们的相关属性，是学习整式后续内容的基础。
整式在几何、实际生活和科学计算中都有重要应用，是表示数量关系的重要工具。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解整式的概念，能说出单项式、多项式、整式之间的联系。
2.能正确识别单项式、多项式、整式，并能准确说出单项式的系
数、次数、多项式的次数和项。
3.能分析具体问题中的数量关系，并能用整式表示，逐步建立数
学符号意识，提升抽象能力。
1.单项式的概念：由数与字母或字母与字母相乘组成的代数式叫作
单项式。单独一个数或一个字母也叫单项式，如0，， 。
单项式中不含加减运算，也不含对字母的开方运算，并且
分母中不含字母，如,, 都不是单项式。
2.单项式的系数：单项式中的数字因数叫作这个单项式的系数。如
的系数是， 的系数是1。
（1）当一个单项式的系数是1或 时，1通常省略不写，
如写成，写成 。（2）当单项式的系数是假分数时，不
要写成带分数，如不要将写成 。（3）单项式的系数包括
前面的符号，如的系数是 。
3.单项式的次数：一个单项式中，所有字母的指数的和叫作这个单
项式的次数。如的次数是1，的次数是 。
（1）常数项的次数规定为零，如1的次数为0；
（2）单独一个字母的次数为1，如 的次数是1。
典例1 （易错题）判断下列各式哪些是单项式,并指出单项式的系
数与次数。
;;;;; 。
解：单项式有，，， 。
单项式
单项式的系数
单项式的次数 1 2
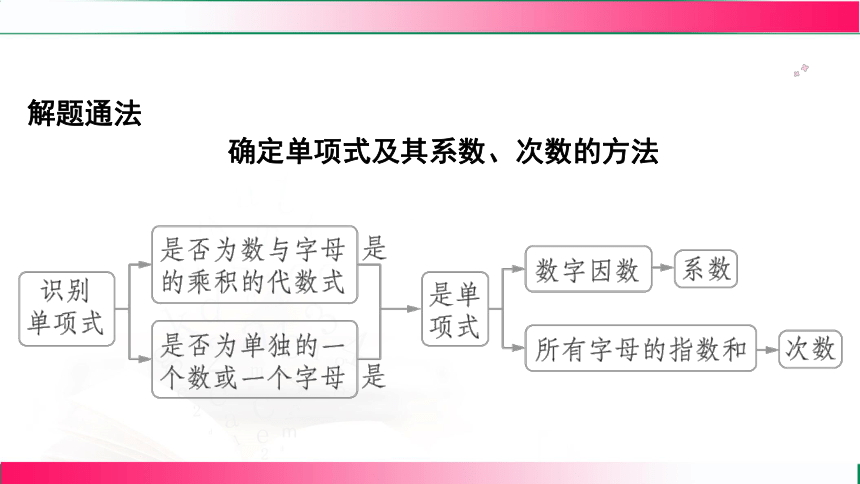
解题通法
确定单项式及其系数、次数的方法
1.多项式的概念：由几个单项式相加组成的代数式叫作多项式。
2.多项式的项：在多项式中，每个单项式叫作多项式的项，不含字
母的项叫作常数项。例如，的项有，， ，常数
项是 。
多项式中的每一项都是单项式，且每一项都包括它前面的
符号，特别注意项的符号为负号时，一定不要漏掉该项的符号。
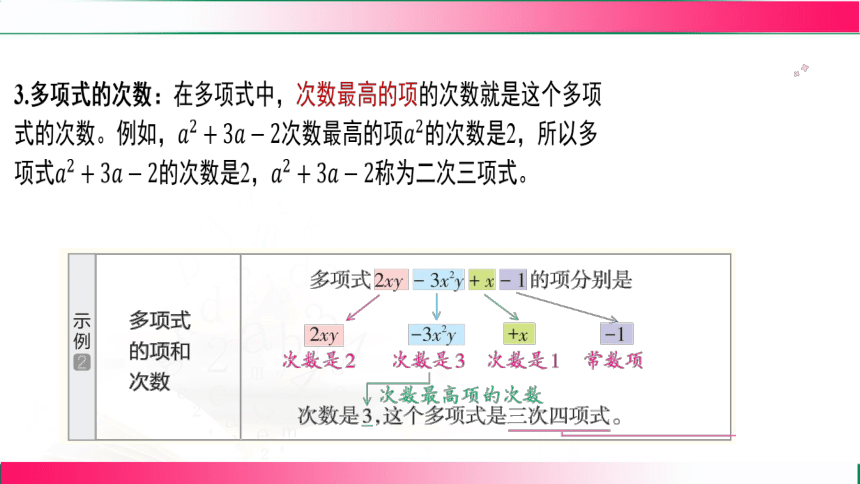
3.多项式的次数：在多项式中，次数最高的项的次数就是这个多项
式的次数。例如，次数最高的项 的次数是2，所以多
项式的次数是2， 称为二次三项式。
典例2 指出下列多项式的项和次数，并说出它是几次几项式。
（1） ；
解：（1）多项式的项分别为,,,
，共四项，最高次项的次数是3,所以它是三次四项式。
（2） 。
（2）多项式 的项分别为， ,共二项，最高次项的次数
是2,所以它是二次二项式。
整式的概念：单项式和多项式统称整式。
整式一定是代数式，但代数式不一定是整式。分母中含
有字母的代数式都不是整式，如代数式 就不是整式。
典例3 下列代数式中哪些是单项式？哪些是多项式？哪些是整式？
，，，，，，，, 。
解：单项式：，，， 。
多项式：，， 。
整式：，，，，，， 。
知识过关
①由 　数与字母或字母与字母相乘　组成的代数式叫作单项
式.单独 　一个数　或 　一个字母　也叫单项式.
②单项式中的 　数字因数　叫作这个单项式的系数.一个单项
式中， 　所有字母的指数的和　叫作这个单项式的次数.
数与字母或字母与字母相乘
一个数
一个字母
数字因数
所有字母的指数的和
③由 　几个单项式相加　组成的代数式叫作多项式.在多项式中，每个单项式叫作多项式的 　项　，不含字母的项叫
作 　常数项　， 　次数最高的项的次数　就是这个多项式的
次数.
④ 　单项式　和 　多项式　统称整式.
几个单项式相加
项
常数项
次数最高的项的次数
单项式
多项式
单项式及其相关概念
1. 在代数式5x＋y， a2b， ， ，0中，是单项式的有
(　A　)
A. 3个 B. 4个
C. 5个 D. 2个
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. [2024·温州龙湾区月考]代数式－3ab2c的系数与次数分别
是(　B　)
A. －3，2 B. －3，4
C. 3，2 D. 3，4
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3. [新视角·结论开放题]写出一个单项式：
，要求此单项式含有字母a，b，系数是3，次数
是3.
4. 已知－8xmy2是一个六次单项式，求－2m＋10的值.
【解】因为－8xmy2是一个六次单项式，
所以m＋2＝6，所以m＝4.
当m＝4时，－2m＋10＝－2×4＋10＝2.
3ab2(或
3a2b)　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
多项式及其相关概念
5. 下列式子是多项式的是(　B　)
D. 4x3
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6. [2024·金华期末]对于多项式x2－5x－6，下列说法正确的
是(　C　)
A. 它是三次三项式
B. 它的常数项是6
C. 它的一次项系数是－5
D. 它的二次项系数是2
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 已知多项式－8x3ym＋xy2－3x3＋6y是六次四项式，则m
的值是 .
8. 填表：
多项式 项数 次数 常数项
3a－1 2 1 －1
－x＋5x2＋7 3 2 7
－2x2y＋6xy2－3 3 3 －3
3　
2
1
－1
3
2
7
3
3
－3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9. [母题 教材P111课内练习]列出表示下列各题结果的代数
式，并指出这些代数式是单项式还是多项式.
(1)某产品前年的产量是n件，去年的产量是前年产量的
m倍，则去年的产量是多少件？
【解】mn件，式子mn是单项式.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)某班总人数为m人，女生人数是男生人数的 ，那么该
班男生人数为多少？
【解】 m人，式子 m是单项式.
(3)妈妈在超市购买物品共需a元，结账时买购物袋又花了
0.5元，妈妈共花了多少元？
【解】(a＋0.5)元，式子a＋0.5是多项式.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
整式
10. [2024·杭州余杭区期末]在 ，2m2n＋5mn2， ，2xy，
－ 中，整式有(　C　)
A. 2个 B. 3个
C. 4个 D. 5个
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. [2023·绍兴期中]已知关于x的整式(｜k｜－3)x3＋(k－
3)x2－k.
(1)若是二次式，求k的值；
【解】因为关于x的整式是二次式，
所以｜k｜－3＝0且k－3≠0，解得k＝－3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)若是二项式，求k的值.
【解】因为关于x的整式是二项式，
所以①｜k｜－3＝0且k－3≠0，解得k＝－3；
②k＝0.故k的值是－3或0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 下列结论正确的是(　B　)
B. 多项式2x2－x＋5是二次三项式
D. 32ab3的次数是6
13. 若多项式xy｜m－n｜＋(n－2)x2y2＋1是关于x，y的三次
多项式，则mn＝ .
B
0或8　
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. 已知单项式－ xy2m－1与－22x2y2的次数相同.
(1)求m的值；
【解】根据题意，得1＋2m－1＝2＋2，
解得m＝2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当x＝－9，y＝－2时，求单项式－ xy2m－1的值.
【解】当m＝2时，－ xy2m－1＝－ xy3.
当x＝－9，y＝－2时，原式＝－ ×(－9)×(－2)3＝
－48.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. [情境题·游戏活动型]游戏规则：(1)每人抽取4张卡片，
如果抽到白色卡片，那么加上卡片上式子最高次项的系
数；如果抽到灰色卡片，那么减去卡片上式子的常数
项；(2)比较两人所抽取的4张卡片的计算结果，结果大
的为胜者.
小玉抽到了如图①的4张卡片：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
小明抽到了如图②的4张卡片：
他们两人谁获胜了？
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】小玉所抽取的卡片的计算结果是－(＋4)＋1－0＋
2＝－1，
小明所抽取的卡片的计算结果是0＋3－(－5)＋(－1)＝7.
因为－1＜7，所以小明获胜.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16. [新视角·规律探究题]观察下列单项式：－x，3x2，－
5x3，7x4，…，－37x19，39x20，….写出第n个单项
式，为了解决这个问题，特提供下面的解题思路.
(1)这组单项式的系数依次为多少？系数的符号规律是什
么？系数的绝对值规律是什么？
【解】这组单项式的系数依次为－1，3，－5，
7，…，系数为奇数且奇次项为负数；系数的符号规
律是(－1)n；系数的绝对值规律是2n－1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)这组单项式的次数的规律是什么？
【解】这组单项式的次数是从1开始的连续自然数.
(3)根据上面的归纳，你可以猜想出第n个单项式是什
么吗？
【解】第n个单项式是(－1)n (2n－1)xn.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(4)请你根据猜想，写出第2 024个、第2 025个单项式.
【解】第2 024个单项式是4 047x2 024，第2 025个单项
式是－4 049x2 025.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看！