4.2 代数式的值 课件(共37张PPT)
文档属性
| 名称 | 4.2 代数式的值 课件(共37张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 00:00:00 | ||
图片预览








文档简介
(共31张PPT)
4.2 代数式的值
第4章 代数式
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
代数式的值
课程目标
理解代数式的值的概念,明确代数式的值与代数式中字母取值的关系。
掌握求代数式值的步骤和方法,能准确求出代数式的值。
了解求代数式值的注意事项,能运用代数式的值解决实际问题。
代数式的值的定义
用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值。
例如,对于代数式\(x + 5\),当\(x = 3\)时,代入可得\(3 + 5 = 8\),那么 8 就是当\(x = 3\)时,代数式\(x + 5\)的值;当\(x=-2\)时,\(-2 + 5 = 3\),3 就是此时该代数式的值。
注意:代数式的值是由代数式中字母的取值决定的,字母的取值不同,代数式的值可能不同。
求代数式值的步骤
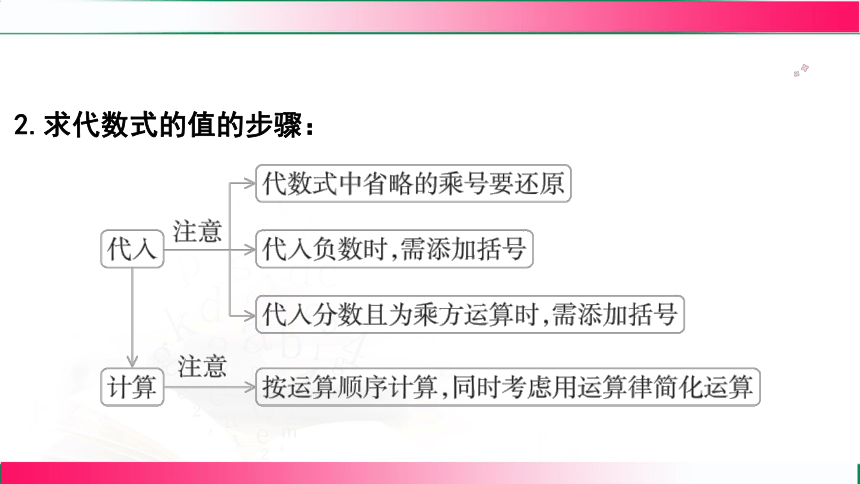
代入:把代数式中字母所取的数值代入代数式中,注意原来的运算符号和数字都要保留。如果字母的值是负数或分数,代入时要加上括号。
例如,求代数式\(2x - 3\)当\(x=-1\)时的值,代入得\(2\times(-1)-3\)。
计算:按照代数式中规定的运算顺序进行计算,得出结果。
接上面的例子,\(2\times(-1)-3=-2 - 3=-5\),所以当\(x=-1\)时,代数式\(2x - 3\)的值是\(-5\)。
求代数式值的方法
直接代入法:直接将字母的取值代入代数式进行计算。这是最基本、最常用的方法。
例如,求代数式\(3a + 2b\)当\(a = 2\),\(b=-1\)时的值,直接代入得\(3\times2 + 2\times(-1)=6-2 = 4\)。
整体代入法:当代数式中字母的取值不易直接求出,或代数式与已知条件存在整体关系时,可将一个代数式作为一个整体代入求值。
例如,已知\(x + y=5\),求代数式\(2(x + y)+3\)的值,把\(x + y\)看作一个整体代入得\(2\times5 + 3=10 + 3=13\)。
化简后代入法:先将代数式进行化简,再代入字母的取值计算,能简化计算过程。
例如,求代数式\(3x^2 + 5x - 2x^2 - x\)当\(x = 3\)时的值,先化简得\((3x^2-2x^2)+(5x - x)=x^2 + 4x\),再代入\(x = 3\)得\(3^2+4\times3=9 + 12=21\)。
实例解析
直接代入计算
求代数式\(x^2 - 2x + 3\)当\(x = 4\)时的值:
代入:\(4^2-2\times4 + 3\)
计算:\(16-8 + 3=11\),所以该代数式的值是 11。
求代数式\(\frac{a - b}{a + b}\)当\(a = 5\),\(b = 2\)时的值:
代入:\(\frac{5 - 2}{5 + 2}\)
计算:\(\frac{3}{7}\),所以该代数式的值是\(\frac{3}{7}\)。
整体代入计算
已知\(a^2 + 2a=3\),求代数式\(2a^2 + 4a + 5\)的值:
观察发现\(2a^2 + 4a=2(a^2 + 2a)\),把\(a^2 + 2a=3\)整体代入得\(2\times3 + 5=6 + 5=11\)。
若\(m - n=3\),求代数式\(4(m - n)-2m + 2n + 5\)的值:
先变形代数式,\(-2m + 2n=-2(m - n)\),则原式可化为\(4(m - n)-2(m - n)+5=2(m - n)+5\),代入\(m - n=3\)得\(2\times3 + 5=11\)。
化简后代入计算
求代数式\(5(x^2y - xy^2)-3(x^2y - xy^2)\)当\(x = 2\),\(y=-1\)时的值:
先化简:\((5 - 3)(x^2y - xy^2)=2(x^2y - xy^2)=2x^2y-2xy^2\)
代入:\(2\times2^2\times(-1)-2\times2\times(-1)^2=2\times4\times(-1)-2\times2\times1=-8 - 4=-12\)
求代数式值的注意事项
代入数值要准确:代入时要注意字母与数值的对应关系,不能代错。例如,代数式\(a + b\)中,\(a = 1\),\(b = 2\),不能代入成\(a = 2\),\(b = 1\)(除非题目允许)。
注意运算顺序:计算时要严格按照代数式中规定的运算顺序进行,先算乘方、开方,再算乘除,最后算加减;有括号的先算括号里的。
符号问题:当字母的取值是负数时,代入后要注意符号的变化。例如,求代数式\(x^2\)当\(x=-3\)时的值,代入得\((-3)^2=9\),不能写成\(-3^2=-9\)。
分数或小数的计算:当字母的取值是分数或小数时,计算要细心,避免出错。例如,求代数式\(2a^2\)当\(a=\frac{1}{2}\)时的值,代入得\(2\times(\frac{1}{2})^2=2\times\frac{1}{4}=\frac{1}{2}\)。
整体代入要合理变形:运用整体代入法时,要对代数式进行适当变形,使其与已知条件的形式一致,以便代入计算。
代数式的值的应用
实际问题计算:在实际生活中,可通过求代数式的值解决与数量相关的问题。例如,某商店的利润计算公式为\(y = 2x - 50\)(其中\(x\)是销售量,\(y\)是利润),当销售量\(x = 100\)时,利润\(y=2\times100 - 50=150\)元,即此时利润为 150 元。
几何问题求解:已知图形的相关代数式,当字母取具体值时,可求出图形的周长、面积等。例如,三角形的面积公式为\(S=\frac{1}{2}ah\)(\(a\)为底,\(h\)为高),当\(a = 6\)厘米,\(h = 4\)厘米时,面积\(S=\frac{1}{2}\times6\times4=12\)平方厘米。
数据分析比较:通过计算不同字母取值时代数式的值,进行数据比较和分析。例如,代数式\(x^2 + 1\),当\(x = 1\)时的值为 2;当\(x = 2\)时的值为 5;当\(x = 0\)时的值为 1,可比较得出当\(x = 2\)时该代数式的值最大。
课堂练习
求下列代数式的值:
代数式\(4x^2 - 2x + 1\),当\(x = 3\)时。
代数式\(\frac{2m + n}{m - n}\),当\(m = 4\),\(n = 1\)时。
已知\(x - 2y=3\),求代数式\(3x - 6y + 5\)的值。
先化简,再求值:代数式\(3(a^2 - ab)-2(a^2 - ab)\),其中\(a = -2\),\(b = 3\)。
总结
代数式的值是用数值代替代数式中的字母后,按运算关系计算得出的结果,其值由字母的取值决定。
求代数式值的步骤为代入和计算,方法有直接代入法、整体代入法和化简后代入法。
求代数式值时要注意代入准确、运算顺序正确、符号无误,整体代入时需合理变形代数式。
代数式的值在实际问题、几何计算和数据分析中都有重要应用,能帮助我们解决具体的数量问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解代数式的值的概念,知道当字母取不同的数值时,代数式
的值一般也不同,体会从抽象到具体的过程。
2.会把具体数代入代数式进行计算,提高运算能力。
1.代数式的值:一般地,用数值代替代数式里的字母,计算后所得
的结果叫作代数式的值。例如,9是代数式当 时的值。
代数式中字母的取值一要保证代数式本身有意义,二要保
证代数式表示的量有意义。例如,中的不能等于0。因为当
时,就没有意义了;表示正方形的边长时, 只能取正数。
2.求代数式的值的步骤:
典例1 已知,,求代数式 的值。
知识过关
一般地,用 数值 代替代数式里的 字母 ,计算后所得
的结果叫作代数式的值.
数值
字母
求代数式的值
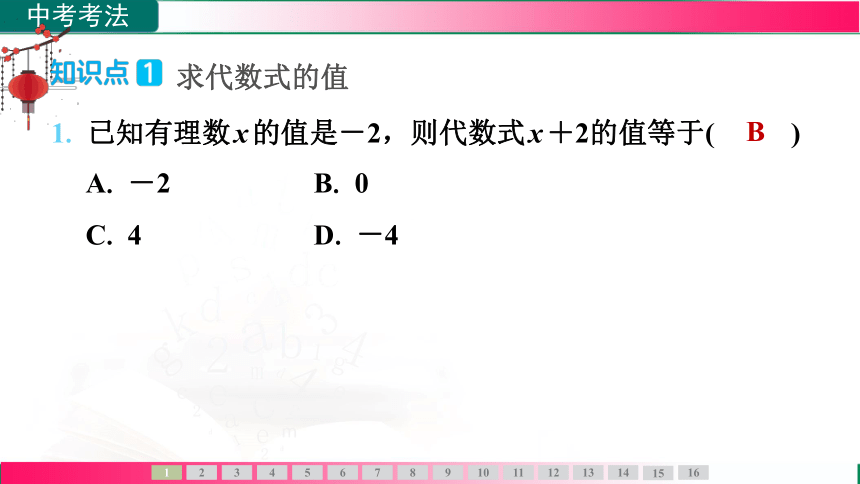
1. 已知有理数x的值是-2,则代数式x+2的值等于( B )
A. -2 B. 0
C. 4 D. -4
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. [2024·温州期末]当a=-1,b=2时,代数式a2-2ab的
值是( D )
A. -5 B. -3
C. 3 D. 5
3. 下列表示a的数中,不能使 +a=0成立的是( B )
A. -0.1 B. 1
C. 0
D
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
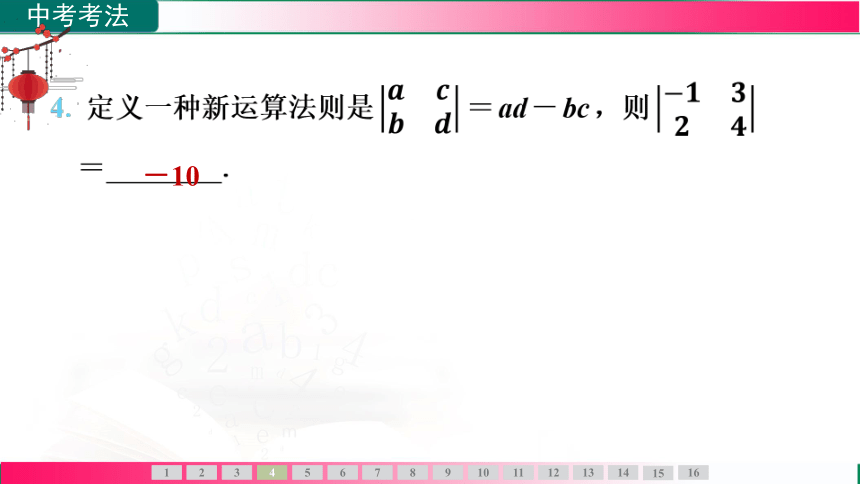
4. 定义一种新运算法则是 =ad-bc,则
= .
-10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)(a-b)2; (2)a2-2ab+b2.
【解】(1)当a=2,b=-3时,
(a-b)2= =52=25.
(2)当a=2,b=-3时,
a2-2ab+b2=22-2×2×(-3)+(-3)2=4+12+9=
25.
5. 当a=2,b=-3时,求下列代数式的值:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
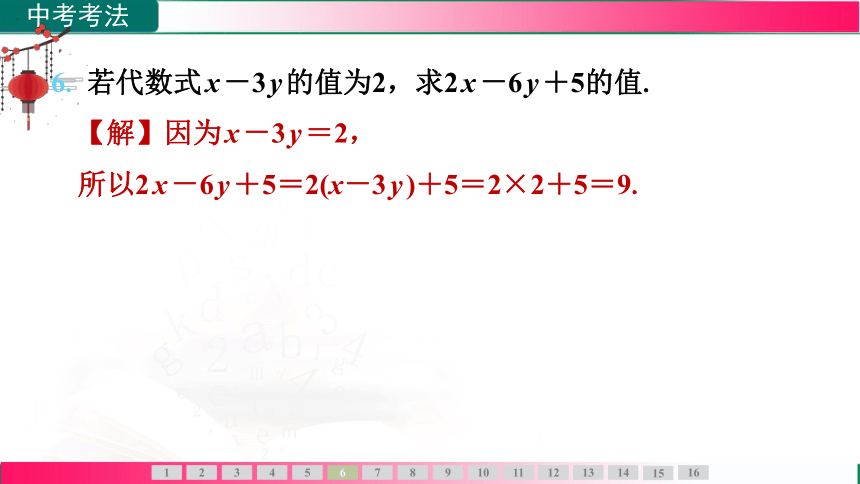
6. 若代数式x-3y的值为2,求2x-6y+5的值.
【解】因为x-3y=2,
所以2x-6y+5=2(x-3y)+5=2×2+5=9.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
代数式求值的简单应用
7. 飞机着陆后滑行t秒的距离为 米,当滑行的
时间为30秒时,滑行的距离为( A )
A. 1 200米 B. 1 100米
C. 1 000米 D. 900米
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. [新趋势跨学科2024广州] 如图,把R1,R2,R3三个电阻
串联起来,线路AB上的电流为I,电压为U,则U=IR1
+IR2+IR3.当R1=20.3,R2=31.9,R3=47.8,I=
2.2时,U的值为 .
220
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9. [情境题生活应用2024衢州期中] 学校组织学生参加红色研
学活动,共有m名教师与n名学生参加.学校咨询了甲、
乙两家旅行社,两家旅行社给出了不同的报价.甲旅行
社:教师全价,80元/人,学生半价,40元/人;乙旅行
社:全部成员,六折优惠,即48元/人.两家旅行社提供的
服务项目与服务质量均相同.
(1)用含m,n的代数式分别表示两家旅行社的收费.
【解】由题意得甲旅行社的收费为(80m+40n)元,乙
旅行社的收费为48(m+n)元.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当m=20,n=500时,选择哪家旅行社更优惠?
【解】当m=20,n=500时,甲旅行社的收费为
80×20+40×500=1 600+20 000=21 600(元),
乙旅行社的收费为48×(20+500)=48×520=24
960(元).
因为21 600<24 960,
所以选择甲旅行社更优惠.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. 若x=-3,y=-2,则x2-2xy+y2的值是( C )
A. -10 B. -2
C. 1 D. 25
【点拨】
当x=-3,y=-2时,
原式=(-3)2-2×(-3)×(-2)+(-2)2=9-12+4
=1.
C
[易错题]代入负数求值时因漏写括号而出错
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. [2024·嘉兴期末]已知2x+y=-6,则代数式9-2y-4x
的值为( A )
A. 21 B. 15
C. 3 D. -3
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 若a是最大的负整数,b是9的算术平方根,m与n互为
倒数,则 -2 024mn的值为 .
13. 有理数a,b,c均不为0,且a+b+c=0,设x=
+ + ,则代数式x2 025+2 025x-2 025
的值为 .
-2 022
1或-4 051
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为有理数a,b,c均不为0,且a+b+c=0,
所以a,b,c不能同为正数或同为负数,故分以下情况
讨论:①三个数中有两个正数,一个负数,设a>0,b
>0,c<0.因为a+b+c=0,所以b+c=-a,c+
a=-b,a+b=-c,所以x= + +
=-1-1+1=-1;
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②三个数中有两个负数,一个正数,设a>0,b<0,c<0.
因为a+b+c=0,所以b+c=-a,c+a=-b,a+b
=-c,所以x= + + =-1+1+1=1.
当x=-1时,原式=(-1)2 025+2 025×(-1)-2 025=-4
051;当x=1时,原式=12 025+2 025×1-2 025=1.综上所
述,答案为1或-4 051.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. 华氏温度f(℉)与摄氏温度c(℃)之间存在如下的关系:f
= c+32.
(1)如果某地早晨的温度为5 ℃,那么此地早晨的华氏温
度是多少?
【解】当c=5时,
f= ×5+32=9+32=41.
答:此地早晨的华氏温度是41 ℉.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)李华对潇潇说:“现在室内的摄氏温度是20 ℃,此时
对应的华氏温度应该是68 ℉.”请你通过计算说明李
华的说法对吗?
【解】当c=20时,f= ×20+32=68.
故李华的说法正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. [新考法·知识情境化] 如图,某学校办公楼前有一块长为
x m,宽为y m的长方形空地,在中心位置留出一个半径
为a的圆形区域建一个喷泉,两边是两个长方形的休息
区,阴影部分为绿地.
(1)用含字母a,b,x,y的式子表示阴影部分的面积
(结果保留π).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】长方形空地的面积是xy m2,圆形区域的面积是πa2 m2,两个长方形的休息区的面积是
2ab m2,所以阴影部分的面积为(xy-πa2-2ab)m2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当x=5,y=4,a=1,b=2时,阴影部分的面积是
多少(π取3)?
【解】当x=5,y=4,a=1,b=2时,
阴影部分的面积为xy-πa2-2ab≈5×4-3×12-2×1×2=13(m2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16. 自从有了用字母表示数,我们发现表达有关的数和数量
关系更加简洁明了,也发现了更多有趣的结论,请你按
要求试一试.
(1)用代数式表示:
①a与b的差的平方;
②a与b两数的平方和与a,b两数积的2倍的差;
【解】①(a-b)2.②a2+b2-2ab.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当a=3,b=-2时,求第(1)题中①②所列的代数式
的值.
【解】当a=3,b=-2时,
(a-b)2=25,a2+b2-2ab=25.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)由第(2)题的结果,你发现了什么等式?
【解】(a-b)2=a2+b2-2ab.
(4)利用你发现的结论,求2 0252-4 050×2 024+2 0242
的值.
【解】原式=2 0252-2×2 025×2 024+2 0242=(2
025-2 024)2=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看!
4.2 代数式的值
第4章 代数式
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
代数式的值
课程目标
理解代数式的值的概念,明确代数式的值与代数式中字母取值的关系。
掌握求代数式值的步骤和方法,能准确求出代数式的值。
了解求代数式值的注意事项,能运用代数式的值解决实际问题。
代数式的值的定义
用数值代替代数式里的字母,按照代数式中的运算关系计算得出的结果,叫做代数式的值。
例如,对于代数式\(x + 5\),当\(x = 3\)时,代入可得\(3 + 5 = 8\),那么 8 就是当\(x = 3\)时,代数式\(x + 5\)的值;当\(x=-2\)时,\(-2 + 5 = 3\),3 就是此时该代数式的值。
注意:代数式的值是由代数式中字母的取值决定的,字母的取值不同,代数式的值可能不同。
求代数式值的步骤
代入:把代数式中字母所取的数值代入代数式中,注意原来的运算符号和数字都要保留。如果字母的值是负数或分数,代入时要加上括号。
例如,求代数式\(2x - 3\)当\(x=-1\)时的值,代入得\(2\times(-1)-3\)。
计算:按照代数式中规定的运算顺序进行计算,得出结果。
接上面的例子,\(2\times(-1)-3=-2 - 3=-5\),所以当\(x=-1\)时,代数式\(2x - 3\)的值是\(-5\)。
求代数式值的方法
直接代入法:直接将字母的取值代入代数式进行计算。这是最基本、最常用的方法。
例如,求代数式\(3a + 2b\)当\(a = 2\),\(b=-1\)时的值,直接代入得\(3\times2 + 2\times(-1)=6-2 = 4\)。
整体代入法:当代数式中字母的取值不易直接求出,或代数式与已知条件存在整体关系时,可将一个代数式作为一个整体代入求值。
例如,已知\(x + y=5\),求代数式\(2(x + y)+3\)的值,把\(x + y\)看作一个整体代入得\(2\times5 + 3=10 + 3=13\)。
化简后代入法:先将代数式进行化简,再代入字母的取值计算,能简化计算过程。
例如,求代数式\(3x^2 + 5x - 2x^2 - x\)当\(x = 3\)时的值,先化简得\((3x^2-2x^2)+(5x - x)=x^2 + 4x\),再代入\(x = 3\)得\(3^2+4\times3=9 + 12=21\)。
实例解析
直接代入计算
求代数式\(x^2 - 2x + 3\)当\(x = 4\)时的值:
代入:\(4^2-2\times4 + 3\)
计算:\(16-8 + 3=11\),所以该代数式的值是 11。
求代数式\(\frac{a - b}{a + b}\)当\(a = 5\),\(b = 2\)时的值:
代入:\(\frac{5 - 2}{5 + 2}\)
计算:\(\frac{3}{7}\),所以该代数式的值是\(\frac{3}{7}\)。
整体代入计算
已知\(a^2 + 2a=3\),求代数式\(2a^2 + 4a + 5\)的值:
观察发现\(2a^2 + 4a=2(a^2 + 2a)\),把\(a^2 + 2a=3\)整体代入得\(2\times3 + 5=6 + 5=11\)。
若\(m - n=3\),求代数式\(4(m - n)-2m + 2n + 5\)的值:
先变形代数式,\(-2m + 2n=-2(m - n)\),则原式可化为\(4(m - n)-2(m - n)+5=2(m - n)+5\),代入\(m - n=3\)得\(2\times3 + 5=11\)。
化简后代入计算
求代数式\(5(x^2y - xy^2)-3(x^2y - xy^2)\)当\(x = 2\),\(y=-1\)时的值:
先化简:\((5 - 3)(x^2y - xy^2)=2(x^2y - xy^2)=2x^2y-2xy^2\)
代入:\(2\times2^2\times(-1)-2\times2\times(-1)^2=2\times4\times(-1)-2\times2\times1=-8 - 4=-12\)
求代数式值的注意事项
代入数值要准确:代入时要注意字母与数值的对应关系,不能代错。例如,代数式\(a + b\)中,\(a = 1\),\(b = 2\),不能代入成\(a = 2\),\(b = 1\)(除非题目允许)。
注意运算顺序:计算时要严格按照代数式中规定的运算顺序进行,先算乘方、开方,再算乘除,最后算加减;有括号的先算括号里的。
符号问题:当字母的取值是负数时,代入后要注意符号的变化。例如,求代数式\(x^2\)当\(x=-3\)时的值,代入得\((-3)^2=9\),不能写成\(-3^2=-9\)。
分数或小数的计算:当字母的取值是分数或小数时,计算要细心,避免出错。例如,求代数式\(2a^2\)当\(a=\frac{1}{2}\)时的值,代入得\(2\times(\frac{1}{2})^2=2\times\frac{1}{4}=\frac{1}{2}\)。
整体代入要合理变形:运用整体代入法时,要对代数式进行适当变形,使其与已知条件的形式一致,以便代入计算。
代数式的值的应用
实际问题计算:在实际生活中,可通过求代数式的值解决与数量相关的问题。例如,某商店的利润计算公式为\(y = 2x - 50\)(其中\(x\)是销售量,\(y\)是利润),当销售量\(x = 100\)时,利润\(y=2\times100 - 50=150\)元,即此时利润为 150 元。
几何问题求解:已知图形的相关代数式,当字母取具体值时,可求出图形的周长、面积等。例如,三角形的面积公式为\(S=\frac{1}{2}ah\)(\(a\)为底,\(h\)为高),当\(a = 6\)厘米,\(h = 4\)厘米时,面积\(S=\frac{1}{2}\times6\times4=12\)平方厘米。
数据分析比较:通过计算不同字母取值时代数式的值,进行数据比较和分析。例如,代数式\(x^2 + 1\),当\(x = 1\)时的值为 2;当\(x = 2\)时的值为 5;当\(x = 0\)时的值为 1,可比较得出当\(x = 2\)时该代数式的值最大。
课堂练习
求下列代数式的值:
代数式\(4x^2 - 2x + 1\),当\(x = 3\)时。
代数式\(\frac{2m + n}{m - n}\),当\(m = 4\),\(n = 1\)时。
已知\(x - 2y=3\),求代数式\(3x - 6y + 5\)的值。
先化简,再求值:代数式\(3(a^2 - ab)-2(a^2 - ab)\),其中\(a = -2\),\(b = 3\)。
总结
代数式的值是用数值代替代数式中的字母后,按运算关系计算得出的结果,其值由字母的取值决定。
求代数式值的步骤为代入和计算,方法有直接代入法、整体代入法和化简后代入法。
求代数式值时要注意代入准确、运算顺序正确、符号无误,整体代入时需合理变形代数式。
代数式的值在实际问题、几何计算和数据分析中都有重要应用,能帮助我们解决具体的数量问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解代数式的值的概念,知道当字母取不同的数值时,代数式
的值一般也不同,体会从抽象到具体的过程。
2.会把具体数代入代数式进行计算,提高运算能力。
1.代数式的值:一般地,用数值代替代数式里的字母,计算后所得
的结果叫作代数式的值。例如,9是代数式当 时的值。
代数式中字母的取值一要保证代数式本身有意义,二要保
证代数式表示的量有意义。例如,中的不能等于0。因为当
时,就没有意义了;表示正方形的边长时, 只能取正数。
2.求代数式的值的步骤:
典例1 已知,,求代数式 的值。
知识过关
一般地,用 数值 代替代数式里的 字母 ,计算后所得
的结果叫作代数式的值.
数值
字母
求代数式的值
1. 已知有理数x的值是-2,则代数式x+2的值等于( B )
A. -2 B. 0
C. 4 D. -4
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. [2024·温州期末]当a=-1,b=2时,代数式a2-2ab的
值是( D )
A. -5 B. -3
C. 3 D. 5
3. 下列表示a的数中,不能使 +a=0成立的是( B )
A. -0.1 B. 1
C. 0
D
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. 定义一种新运算法则是 =ad-bc,则
= .
-10
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)(a-b)2; (2)a2-2ab+b2.
【解】(1)当a=2,b=-3时,
(a-b)2= =52=25.
(2)当a=2,b=-3时,
a2-2ab+b2=22-2×2×(-3)+(-3)2=4+12+9=
25.
5. 当a=2,b=-3时,求下列代数式的值:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
6. 若代数式x-3y的值为2,求2x-6y+5的值.
【解】因为x-3y=2,
所以2x-6y+5=2(x-3y)+5=2×2+5=9.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
代数式求值的简单应用
7. 飞机着陆后滑行t秒的距离为 米,当滑行的
时间为30秒时,滑行的距离为( A )
A. 1 200米 B. 1 100米
C. 1 000米 D. 900米
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. [新趋势跨学科2024广州] 如图,把R1,R2,R3三个电阻
串联起来,线路AB上的电流为I,电压为U,则U=IR1
+IR2+IR3.当R1=20.3,R2=31.9,R3=47.8,I=
2.2时,U的值为 .
220
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
9. [情境题生活应用2024衢州期中] 学校组织学生参加红色研
学活动,共有m名教师与n名学生参加.学校咨询了甲、
乙两家旅行社,两家旅行社给出了不同的报价.甲旅行
社:教师全价,80元/人,学生半价,40元/人;乙旅行
社:全部成员,六折优惠,即48元/人.两家旅行社提供的
服务项目与服务质量均相同.
(1)用含m,n的代数式分别表示两家旅行社的收费.
【解】由题意得甲旅行社的收费为(80m+40n)元,乙
旅行社的收费为48(m+n)元.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当m=20,n=500时,选择哪家旅行社更优惠?
【解】当m=20,n=500时,甲旅行社的收费为
80×20+40×500=1 600+20 000=21 600(元),
乙旅行社的收费为48×(20+500)=48×520=24
960(元).
因为21 600<24 960,
所以选择甲旅行社更优惠.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. 若x=-3,y=-2,则x2-2xy+y2的值是( C )
A. -10 B. -2
C. 1 D. 25
【点拨】
当x=-3,y=-2时,
原式=(-3)2-2×(-3)×(-2)+(-2)2=9-12+4
=1.
C
[易错题]代入负数求值时因漏写括号而出错
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. [2024·嘉兴期末]已知2x+y=-6,则代数式9-2y-4x
的值为( A )
A. 21 B. 15
C. 3 D. -3
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 若a是最大的负整数,b是9的算术平方根,m与n互为
倒数,则 -2 024mn的值为 .
13. 有理数a,b,c均不为0,且a+b+c=0,设x=
+ + ,则代数式x2 025+2 025x-2 025
的值为 .
-2 022
1或-4 051
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为有理数a,b,c均不为0,且a+b+c=0,
所以a,b,c不能同为正数或同为负数,故分以下情况
讨论:①三个数中有两个正数,一个负数,设a>0,b
>0,c<0.因为a+b+c=0,所以b+c=-a,c+
a=-b,a+b=-c,所以x= + +
=-1-1+1=-1;
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
②三个数中有两个负数,一个正数,设a>0,b<0,c<0.
因为a+b+c=0,所以b+c=-a,c+a=-b,a+b
=-c,所以x= + + =-1+1+1=1.
当x=-1时,原式=(-1)2 025+2 025×(-1)-2 025=-4
051;当x=1时,原式=12 025+2 025×1-2 025=1.综上所
述,答案为1或-4 051.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. 华氏温度f(℉)与摄氏温度c(℃)之间存在如下的关系:f
= c+32.
(1)如果某地早晨的温度为5 ℃,那么此地早晨的华氏温
度是多少?
【解】当c=5时,
f= ×5+32=9+32=41.
答:此地早晨的华氏温度是41 ℉.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)李华对潇潇说:“现在室内的摄氏温度是20 ℃,此时
对应的华氏温度应该是68 ℉.”请你通过计算说明李
华的说法对吗?
【解】当c=20时,f= ×20+32=68.
故李华的说法正确.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. [新考法·知识情境化] 如图,某学校办公楼前有一块长为
x m,宽为y m的长方形空地,在中心位置留出一个半径
为a的圆形区域建一个喷泉,两边是两个长方形的休息
区,阴影部分为绿地.
(1)用含字母a,b,x,y的式子表示阴影部分的面积
(结果保留π).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】长方形空地的面积是xy m2,圆形区域的面积是πa2 m2,两个长方形的休息区的面积是
2ab m2,所以阴影部分的面积为(xy-πa2-2ab)m2.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当x=5,y=4,a=1,b=2时,阴影部分的面积是
多少(π取3)?
【解】当x=5,y=4,a=1,b=2时,
阴影部分的面积为xy-πa2-2ab≈5×4-3×12-2×1×2=13(m2).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16. 自从有了用字母表示数,我们发现表达有关的数和数量
关系更加简洁明了,也发现了更多有趣的结论,请你按
要求试一试.
(1)用代数式表示:
①a与b的差的平方;
②a与b两数的平方和与a,b两数积的2倍的差;
【解】①(a-b)2.②a2+b2-2ab.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)当a=3,b=-2时,求第(1)题中①②所列的代数式
的值.
【解】当a=3,b=-2时,
(a-b)2=25,a2+b2-2ab=25.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)由第(2)题的结果,你发现了什么等式?
【解】(a-b)2=a2+b2-2ab.
(4)利用你发现的结论,求2 0252-4 050×2 024+2 0242
的值.
【解】原式=2 0252-2×2 025×2 024+2 0242=(2
025-2 024)2=1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
