4.4 合并同类项 课件(共35张PPT)
文档属性
| 名称 | 4.4 合并同类项 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 12:10:13 | ||
图片预览











文档简介
(共35张PPT)
4.4 合并同类项
第4章 代数式
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
合并同类项
课程目标
理解同类项的概念,能准确判断几个单项式是否为同类项。
掌握合并同类项的法则和步骤,能熟练进行同类项的合并。
了解合并同类项在化简代数式中的作用,会运用合并同类项解决相关问题。
同类项的定义
所含字母相同,并且相同字母的指数也相同的项叫做同类项。几个常数项也是同类项。
例如:\(3x\)与\(-5x\),所含字母都是\(x\),且\(x\)的指数都是\(1\),是同类项;\(2xy^2\)与\(-7xy^2\),所含字母都是\(x\)、\(y\),\(x\)的指数都是\(1\),\(y\)的指数都是\(2\),是同类项;\(5\)与\(-3\)都是常数项,是同类项。
注意:同类项与系数无关,与字母的排列顺序无关。例如,\(3a^2b\)与\(-5ba^2\)是同类项,因为它们所含字母相同,相同字母的指数也相同,只是字母的排列顺序不同。
同类项的特征
两相同:
所含字母相同。
相同字母的指数相同。
两无关:
与系数无关。
与字母的排列顺序无关。
合并同类项的概念
把多项式中的同类项合并成一项,叫做合并同类项。合并同类项的过程实际上是逆用乘法分配律,即\(ac + bc=(a + b)c\)。
例如:\(3x + 5x=(3 + 5)x=8x\),这里就是把同类项\(3x\)和\(5x\)合并成了一项\(8x\)。
合并同类项的法则
合并同类项时,把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变。
例如:合并同类项\(2a^2b + 3a^2b\),系数相加为\(2 + 3=5\),字母和字母的指数不变,所以结果为\(5a^2b\);合并同类项\(-4xy - 6xy\),系数相加为\(-4+(-6)=-10\),结果为\(-10xy\)。
合并同类项的步骤
找:找出多项式中的同类项,可以用不同的符号标出不同的同类项。
移:根据加法交换律和结合律,将同类项移到一起,注意移动时要连同项的符号一起移动。
合:按照合并同类项的法则,将同类项的系数相加,字母和字母的指数不变。
查:检查合并后的结果是否还有同类项,若有则继续合并,直到没有同类项为止。
实例演示
合并多项式\(3x^2 + 2xy - 5x^2 + 4xy\)的同类项:
找:同类项有\(3x^2\)与\(-5x^2\),\(2xy\)与\(4xy\)。
移:将同类项移到一起,得到\(3x^2 - 5x^2 + 2xy + 4xy\)。
合:合并同类项,\((3 - 5)x^2+(2 + 4)xy=-2x^2 + 6xy\)。
查:检查结果\(-2x^2 + 6xy\),没有同类项,合并完成。
再如,合并多项式\(5a - 3b - 2a + 4b + 1\)的同类项:
找:同类项有\(5a\)与\(-2a\),\(-3b\)与\(4b\)。
移:移项后得到\(5a - 2a - 3b + 4b + 1\)。
合:合并同类项,\((5 - 2)a+(-3 + 4)b + 1=3a + b + 1\)。
查:结果中没有同类项,合并完成。
合并同类项的注意事项
合并同类项时,只能把同类项合并:不是同类项的不能合并。例如,\(2x + 3y\)不能合并,因为它们不是同类项。
合并同类项后,所得项的系数是合并前各同类项系数的和:字母和字母的指数与合并前保持一致。
系数相加时要注意符号:尤其是系数为负数时,不能漏加负号。例如,合并\(-3x^2 + 5x^2\)时,系数相加为\(-3 + 5=2\),结果为\(2x^2\)。
多项式中只有同类项才能合并:合并后的多项式的项数可能比原来的少,但次数不会高于原来多项式的次数。
合并同类项的应用
化简代数式:通过合并同类项可以将复杂的多项式化简,使代数式更加简洁。例如,化简多项式\(4x^2 + 3x - 2x^2 - 5x + 1\),合并同类项后得到\((4x^2 - 2x^2)+(3x - 5x)+1=2x^2 - 2x + 1\),化简后的式子更便于计算和分析。
求代数式的值:先合并同类项化简代数式,再代入数值计算,可简化计算过程。例如,求代数式\(3a^2 + 2ab - 5a^2 + ab\)当\(a = 2\),\(b=-1\)时的值,先合并同类项得\((3a^2 - 5a^2)+(2ab + ab)=-2a^2 + 3ab\),再代入得\(-2\times2^2 + 3\times2\times(-1)=-8-6=-14\)。
实际问题解决:在实际问题中,用多项式表示数量关系后,通过合并同类项可以简化式子,便于进一步分析和计算。例如,一个长方形的长为\(3x + 2\),宽为\(x - 1\),它的周长为\(2[(3x + 2)+(x - 1)]=2[3x + 2 + x - 1]=2[(3x + x)+(2 - 1)]=2[4x + 1]=8x + 2\),通过合并同类项简化了周长的表达式。
课堂练习
指出下列多项式中的同类项:
\(3x - 2y + 1 + 3y - 2x - 5\)
\(5a^2b - 3ab^2 + 2a^2b - ab^2\)
合并下列多项式中的同类项:
\(4m^2 + 3m - m^2 - 5m\)
\(6x^2y + 2xy - 8x^2y - 5xy + 1\)
先合并同类项,再求值:
代数式\(3x^2 - 4x + 5 - 2x^2 + x - 1\),其中\(x = -2\)。
总结
同类项是所含字母相同且相同字母的指数也相同的项,与系数和字母排列顺序无关。
合并同类项就是把同类项的系数相加,字母和字母的指数不变,步骤为找、移、合、查。
合并同类项能化简代数式,方便求值和解决实际问题,是整式运算的重要基础。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解同类项的概念。
2.掌握合并同类项的方法,能正确地合并同类项。
3.会利用合并同类项法则进行整式化简。
同类项:多项式中,所含字母相同,并且相同字母的指数也相同的
项,叫作同类项。所有常数项也看作同类项。
敲黑板
判断同类项时的“两相同,两无关”
典例1 给出各组单项式:与;与; 与
; 与0。其中是同类项的有( )
B
A.4组 B.3组 C.2组 D.1组
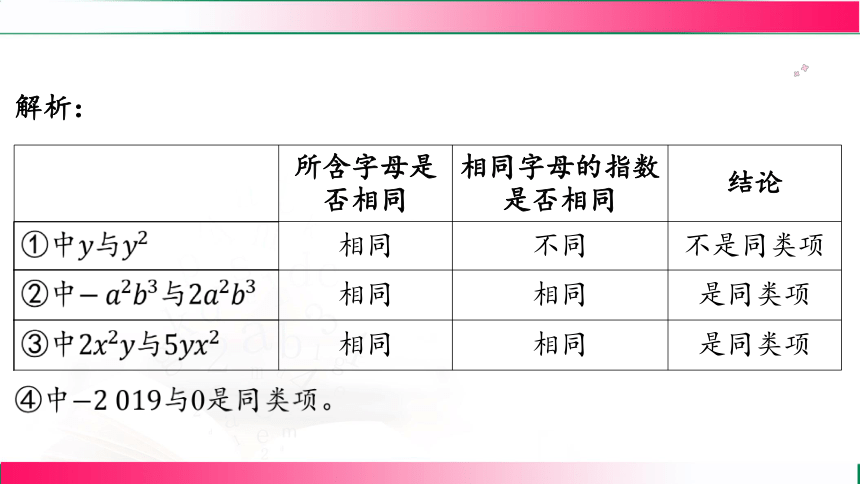
解析:
所含字母是 否相同 相同字母的指数 是否相同 结论
相同 不同 不是同类项
相同 相同 是同类项
相同 相同 是同类项
④中 与0是同类项。
1.合并同类项:把多项式中的同类项合并成一项,叫作合并同类项。
2.合并同类项的法则:把同类项的系数相加,所得结果作为系数,
字母和字母的指数不变。
3.合并同类项的一般步骤:
典例2 合并同类项:
(1) ;
(2) 。
典例2 合并同类项:
(1) ;
(2) 。
知识过关
①多项式中,所含 字母 相同,并且相同字母的 指数 也
相同的项,叫作同类项.
②所有常数项也看作 同类项 .把多项式中的同类项合并成
一项,叫作 合并同类项 .
③合并同类项法则:把同类项的系数相加,所得结果作为 系
数 ,字母和字母的 指数 不变.
字母
指数
同类项
合并同类项
系
数
指数
同类项的概念
1. [2024·内江]下列单项式中,ab3的同类项是( A )
A. 3ab3 B. 2a2b3
C. -a2b2 D. a3b
2. 下列各组整式中,不是同类项的是( D )
A. mn与2mn B. 23与32
D. ab2与a2b
A
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. [新视角·结论开放题][2024·河南]请写出2m的一个同类
项: .
4. [2024·湖州期末]若单项式3xym与-xny3是同类项,则n-
m的值是 .
m(答案不唯一)
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(1)-x2y与 x2y;
【解】-x2y与 x2y是同类项,因为-x2y与 x2y
都含有x和y,且x的指数都是2,y的指数都是1.
23与-34是同类项,因为23与-34都不含字母,为常
数项.常数项都是同类项.
5. [母题 教材P114做一做T1]下列各题中的两项是不是同类项?为什么?
(2)23与-34;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】2a3b2与3a2b3不是同类项,因为2a3b2与3a2b3中,a的指数分别是3和2,b的指数分别是2和3,所以不是同类项.
【解】 xyz与3xy不是同类项,因为 xyz与3xy中所含字母不同, xyz含有字母x,y,z,而3xy中含有字母x,y,所以不是同类项.
(3)2a3b2与3a2b3;
(4) xyz与3xy.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
合并同类项法则
6. [2023·丽水]计算a2+2a2的正确结果是( C )
A. 2a2 B. 2a4
C. 3a2 D. 3a4
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. [2024·嘉兴期末]下列计算正确的是( C )
A. 3a+2b=5ab
B. 5xy-4xy=1
C. 3x2-(-x2)=4x2
D. -6ab2+3ab2=-9ab2
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8. [立德树人·教育政策]为了推进“双减”政策,某校开展了
丰富多彩的拓展课程,每名学生可以选择一门课程.已知
选择烘焙课程的有m人,选择小小工匠课程的人数比烘
焙课程人数少10人,选择田园达人课程的人数比小小工匠
课程人数的2倍多3人,则选择这三门拓展课程的总人数为
( A )
A
A. (4m-27)人 B. (4m+27)人
C. (3m+7)人 D. (3m-7)人
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. 合并同类项:
(1)3x-2y+5x-y;
【解】原式=(3x+5x)+(-2y-y)
=8x-3y.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)0.8a2b-6ab-3.2a2b+5ab+a2b;
【解】原式=(0.8a2b-3.2a2b+a2b)+(-6ab+
5ab)
=-1.4a2b-ab.
(3)5x3-3x2+2x-x3+6x2.
【解】原式=(5x3-x3)+(-3x2+6x2)+2x
=4x3+3x2+2x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10. [母题 教材P114例]当x=- ,y=0.25时,求代数式2x
-7y-5x+11y-1的值.
【解】原式=(2x-5x)+(-7y+11y)-1
=-3x+4y-1.
当x=- ,y=0.25时,原式=-3× +4×0.25
-1= +1-1= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
11. 要使多项式3x2-10-2x-4x2+mx2化简后不含x的二
次项,则m的值为( B )
A. 0 B. 1
C. -1 D. -7
12. [2024·金华月考]如果单项式x2ym+2与xny的和仍然是一
个单项式,则5x2ym+2-3xny= (结果不含m和
n).
B
2x2y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13. [情境题·生活应用]如图是一个长方形场地,它的长是6a
米,宽是3b米.其中除半圆形休息区和长方形游泳区以
外的地方都是绿地.已知半圆形休息区的直径为2a米,
长方形游泳区的长是3a米,宽是b米.(π取3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(1)用代数式表示绿地的面积;
【解】绿地的面积为
6a×3b-3a×b- π ≈ 平方米.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)当a=3,b=2时,求绿地的面积.
【解】当a=3,b=2时,
15ab- a2=15×3×2- ×32= .
所以绿地的面积是 平方米.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. [新考法·阅读类比法]阅读材料:我们知道,4x-2x+x
=(4-2+1)x=3x,类似地,我们把(a+b)看成一个整
体,则4(a+b)-2(a+b)+(a+b)=(4-2+1)(a+b)=
3(a+b).“整体思想”是中学数学解题中的一种重要的
思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(1)把(a-b)2看成一个整体,化简3(a-b)2+6(a-b)2-
2(a-b)2;
【解】3(a-b)2+6(a-b)2-2(a-b)2=(3+6-2)(a
-b)2=7(a-b)2.
(2)已知a=3,b=4,求3(a-b)2+6(a-b)2-2(a-b)2
的值.
【解】当a=3,b=4时,
原式=7(a-b)2=7×(3-4)2=7×1=7.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. [新视角·新定义题][2024·嘉兴期中]类比同类项的概念,
我们规定:所含字母相同,并且相同字母的指数之差的
绝对值等于0或1的项是“强同类项”,例如:-x3y4与
2x4y3是“强同类项”.
(1)给出下列四个单项式:①5x2y5;②-x5y5;③
4x4y4;④-2x3y6.其中与x4y5是“强同类项”的
是 (填写序号);
②③④
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)若x3y4zm-2与-2x2y3z6是“强同类项”,求m的值;
【解】因为x3y4zm-2与-2x2y3z6是“强同类项”,
所以m-2=5或6或7,
所以m=7或8或9.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)已知2a2bs,3atb4均为关于a,b的单项式,其中s
=|x-1|+k,t=2k,如果2a2bs,3atb4是“强
同类项”,那么x的最大值是 ,最小值是
.
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为2a2bs,3atb4是“强同类项”,所以s=3或4
或5,t=1或2或3.
因为t=2k,所以k= 或1或 .
因为s=|x-1|+k,所以|x-1|=s-k.
当s取最大值,k取最小值时,|x-1|取得最
大值,此时x有最大值和最小值,
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
即当s=5,k= 时,|x-1|取得最大值 ,
此时x= 或- ,
所以x的最大值是 ,最小值是- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
谢谢观看!
4.4 合并同类项
第4章 代数式
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
合并同类项
课程目标
理解同类项的概念,能准确判断几个单项式是否为同类项。
掌握合并同类项的法则和步骤,能熟练进行同类项的合并。
了解合并同类项在化简代数式中的作用,会运用合并同类项解决相关问题。
同类项的定义
所含字母相同,并且相同字母的指数也相同的项叫做同类项。几个常数项也是同类项。
例如:\(3x\)与\(-5x\),所含字母都是\(x\),且\(x\)的指数都是\(1\),是同类项;\(2xy^2\)与\(-7xy^2\),所含字母都是\(x\)、\(y\),\(x\)的指数都是\(1\),\(y\)的指数都是\(2\),是同类项;\(5\)与\(-3\)都是常数项,是同类项。
注意:同类项与系数无关,与字母的排列顺序无关。例如,\(3a^2b\)与\(-5ba^2\)是同类项,因为它们所含字母相同,相同字母的指数也相同,只是字母的排列顺序不同。
同类项的特征
两相同:
所含字母相同。
相同字母的指数相同。
两无关:
与系数无关。
与字母的排列顺序无关。
合并同类项的概念
把多项式中的同类项合并成一项,叫做合并同类项。合并同类项的过程实际上是逆用乘法分配律,即\(ac + bc=(a + b)c\)。
例如:\(3x + 5x=(3 + 5)x=8x\),这里就是把同类项\(3x\)和\(5x\)合并成了一项\(8x\)。
合并同类项的法则
合并同类项时,把同类项的系数相加,所得的结果作为系数,字母和字母的指数保持不变。
例如:合并同类项\(2a^2b + 3a^2b\),系数相加为\(2 + 3=5\),字母和字母的指数不变,所以结果为\(5a^2b\);合并同类项\(-4xy - 6xy\),系数相加为\(-4+(-6)=-10\),结果为\(-10xy\)。
合并同类项的步骤
找:找出多项式中的同类项,可以用不同的符号标出不同的同类项。
移:根据加法交换律和结合律,将同类项移到一起,注意移动时要连同项的符号一起移动。
合:按照合并同类项的法则,将同类项的系数相加,字母和字母的指数不变。
查:检查合并后的结果是否还有同类项,若有则继续合并,直到没有同类项为止。
实例演示
合并多项式\(3x^2 + 2xy - 5x^2 + 4xy\)的同类项:
找:同类项有\(3x^2\)与\(-5x^2\),\(2xy\)与\(4xy\)。
移:将同类项移到一起,得到\(3x^2 - 5x^2 + 2xy + 4xy\)。
合:合并同类项,\((3 - 5)x^2+(2 + 4)xy=-2x^2 + 6xy\)。
查:检查结果\(-2x^2 + 6xy\),没有同类项,合并完成。
再如,合并多项式\(5a - 3b - 2a + 4b + 1\)的同类项:
找:同类项有\(5a\)与\(-2a\),\(-3b\)与\(4b\)。
移:移项后得到\(5a - 2a - 3b + 4b + 1\)。
合:合并同类项,\((5 - 2)a+(-3 + 4)b + 1=3a + b + 1\)。
查:结果中没有同类项,合并完成。
合并同类项的注意事项
合并同类项时,只能把同类项合并:不是同类项的不能合并。例如,\(2x + 3y\)不能合并,因为它们不是同类项。
合并同类项后,所得项的系数是合并前各同类项系数的和:字母和字母的指数与合并前保持一致。
系数相加时要注意符号:尤其是系数为负数时,不能漏加负号。例如,合并\(-3x^2 + 5x^2\)时,系数相加为\(-3 + 5=2\),结果为\(2x^2\)。
多项式中只有同类项才能合并:合并后的多项式的项数可能比原来的少,但次数不会高于原来多项式的次数。
合并同类项的应用
化简代数式:通过合并同类项可以将复杂的多项式化简,使代数式更加简洁。例如,化简多项式\(4x^2 + 3x - 2x^2 - 5x + 1\),合并同类项后得到\((4x^2 - 2x^2)+(3x - 5x)+1=2x^2 - 2x + 1\),化简后的式子更便于计算和分析。
求代数式的值:先合并同类项化简代数式,再代入数值计算,可简化计算过程。例如,求代数式\(3a^2 + 2ab - 5a^2 + ab\)当\(a = 2\),\(b=-1\)时的值,先合并同类项得\((3a^2 - 5a^2)+(2ab + ab)=-2a^2 + 3ab\),再代入得\(-2\times2^2 + 3\times2\times(-1)=-8-6=-14\)。
实际问题解决:在实际问题中,用多项式表示数量关系后,通过合并同类项可以简化式子,便于进一步分析和计算。例如,一个长方形的长为\(3x + 2\),宽为\(x - 1\),它的周长为\(2[(3x + 2)+(x - 1)]=2[3x + 2 + x - 1]=2[(3x + x)+(2 - 1)]=2[4x + 1]=8x + 2\),通过合并同类项简化了周长的表达式。
课堂练习
指出下列多项式中的同类项:
\(3x - 2y + 1 + 3y - 2x - 5\)
\(5a^2b - 3ab^2 + 2a^2b - ab^2\)
合并下列多项式中的同类项:
\(4m^2 + 3m - m^2 - 5m\)
\(6x^2y + 2xy - 8x^2y - 5xy + 1\)
先合并同类项,再求值:
代数式\(3x^2 - 4x + 5 - 2x^2 + x - 1\),其中\(x = -2\)。
总结
同类项是所含字母相同且相同字母的指数也相同的项,与系数和字母排列顺序无关。
合并同类项就是把同类项的系数相加,字母和字母的指数不变,步骤为找、移、合、查。
合并同类项能化简代数式,方便求值和解决实际问题,是整式运算的重要基础。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解同类项的概念。
2.掌握合并同类项的方法,能正确地合并同类项。
3.会利用合并同类项法则进行整式化简。
同类项:多项式中,所含字母相同,并且相同字母的指数也相同的
项,叫作同类项。所有常数项也看作同类项。
敲黑板
判断同类项时的“两相同,两无关”
典例1 给出各组单项式:与;与; 与
; 与0。其中是同类项的有( )
B
A.4组 B.3组 C.2组 D.1组
解析:
所含字母是 否相同 相同字母的指数 是否相同 结论
相同 不同 不是同类项
相同 相同 是同类项
相同 相同 是同类项
④中 与0是同类项。
1.合并同类项:把多项式中的同类项合并成一项,叫作合并同类项。
2.合并同类项的法则:把同类项的系数相加,所得结果作为系数,
字母和字母的指数不变。
3.合并同类项的一般步骤:
典例2 合并同类项:
(1) ;
(2) 。
典例2 合并同类项:
(1) ;
(2) 。
知识过关
①多项式中,所含 字母 相同,并且相同字母的 指数 也
相同的项,叫作同类项.
②所有常数项也看作 同类项 .把多项式中的同类项合并成
一项,叫作 合并同类项 .
③合并同类项法则:把同类项的系数相加,所得结果作为 系
数 ,字母和字母的 指数 不变.
字母
指数
同类项
合并同类项
系
数
指数
同类项的概念
1. [2024·内江]下列单项式中,ab3的同类项是( A )
A. 3ab3 B. 2a2b3
C. -a2b2 D. a3b
2. 下列各组整式中,不是同类项的是( D )
A. mn与2mn B. 23与32
D. ab2与a2b
A
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
3. [新视角·结论开放题][2024·河南]请写出2m的一个同类
项: .
4. [2024·湖州期末]若单项式3xym与-xny3是同类项,则n-
m的值是 .
m(答案不唯一)
-2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(1)-x2y与 x2y;
【解】-x2y与 x2y是同类项,因为-x2y与 x2y
都含有x和y,且x的指数都是2,y的指数都是1.
23与-34是同类项,因为23与-34都不含字母,为常
数项.常数项都是同类项.
5. [母题 教材P114做一做T1]下列各题中的两项是不是同类项?为什么?
(2)23与-34;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
【解】2a3b2与3a2b3不是同类项,因为2a3b2与3a2b3中,a的指数分别是3和2,b的指数分别是2和3,所以不是同类项.
【解】 xyz与3xy不是同类项,因为 xyz与3xy中所含字母不同, xyz含有字母x,y,z,而3xy中含有字母x,y,所以不是同类项.
(3)2a3b2与3a2b3;
(4) xyz与3xy.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
合并同类项法则
6. [2023·丽水]计算a2+2a2的正确结果是( C )
A. 2a2 B. 2a4
C. 3a2 D. 3a4
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
7. [2024·嘉兴期末]下列计算正确的是( C )
A. 3a+2b=5ab
B. 5xy-4xy=1
C. 3x2-(-x2)=4x2
D. -6ab2+3ab2=-9ab2
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
8. [立德树人·教育政策]为了推进“双减”政策,某校开展了
丰富多彩的拓展课程,每名学生可以选择一门课程.已知
选择烘焙课程的有m人,选择小小工匠课程的人数比烘
焙课程人数少10人,选择田园达人课程的人数比小小工匠
课程人数的2倍多3人,则选择这三门拓展课程的总人数为
( A )
A
A. (4m-27)人 B. (4m+27)人
C. (3m+7)人 D. (3m-7)人
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
9. 合并同类项:
(1)3x-2y+5x-y;
【解】原式=(3x+5x)+(-2y-y)
=8x-3y.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)0.8a2b-6ab-3.2a2b+5ab+a2b;
【解】原式=(0.8a2b-3.2a2b+a2b)+(-6ab+
5ab)
=-1.4a2b-ab.
(3)5x3-3x2+2x-x3+6x2.
【解】原式=(5x3-x3)+(-3x2+6x2)+2x
=4x3+3x2+2x.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
10. [母题 教材P114例]当x=- ,y=0.25时,求代数式2x
-7y-5x+11y-1的值.
【解】原式=(2x-5x)+(-7y+11y)-1
=-3x+4y-1.
当x=- ,y=0.25时,原式=-3× +4×0.25
-1= +1-1= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
11. 要使多项式3x2-10-2x-4x2+mx2化简后不含x的二
次项,则m的值为( B )
A. 0 B. 1
C. -1 D. -7
12. [2024·金华月考]如果单项式x2ym+2与xny的和仍然是一
个单项式,则5x2ym+2-3xny= (结果不含m和
n).
B
2x2y
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
13. [情境题·生活应用]如图是一个长方形场地,它的长是6a
米,宽是3b米.其中除半圆形休息区和长方形游泳区以
外的地方都是绿地.已知半圆形休息区的直径为2a米,
长方形游泳区的长是3a米,宽是b米.(π取3)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(1)用代数式表示绿地的面积;
【解】绿地的面积为
6a×3b-3a×b- π ≈ 平方米.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)当a=3,b=2时,求绿地的面积.
【解】当a=3,b=2时,
15ab- a2=15×3×2- ×32= .
所以绿地的面积是 平方米.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
14. [新考法·阅读类比法]阅读材料:我们知道,4x-2x+x
=(4-2+1)x=3x,类似地,我们把(a+b)看成一个整
体,则4(a+b)-2(a+b)+(a+b)=(4-2+1)(a+b)=
3(a+b).“整体思想”是中学数学解题中的一种重要的
思想方法,它在多项式的化简与求值中应用极为广泛.
尝试应用:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(1)把(a-b)2看成一个整体,化简3(a-b)2+6(a-b)2-
2(a-b)2;
【解】3(a-b)2+6(a-b)2-2(a-b)2=(3+6-2)(a
-b)2=7(a-b)2.
(2)已知a=3,b=4,求3(a-b)2+6(a-b)2-2(a-b)2
的值.
【解】当a=3,b=4时,
原式=7(a-b)2=7×(3-4)2=7×1=7.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
15. [新视角·新定义题][2024·嘉兴期中]类比同类项的概念,
我们规定:所含字母相同,并且相同字母的指数之差的
绝对值等于0或1的项是“强同类项”,例如:-x3y4与
2x4y3是“强同类项”.
(1)给出下列四个单项式:①5x2y5;②-x5y5;③
4x4y4;④-2x3y6.其中与x4y5是“强同类项”的
是 (填写序号);
②③④
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(2)若x3y4zm-2与-2x2y3z6是“强同类项”,求m的值;
【解】因为x3y4zm-2与-2x2y3z6是“强同类项”,
所以m-2=5或6或7,
所以m=7或8或9.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
(3)已知2a2bs,3atb4均为关于a,b的单项式,其中s
=|x-1|+k,t=2k,如果2a2bs,3atb4是“强
同类项”,那么x的最大值是 ,最小值是
.
-
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
因为2a2bs,3atb4是“强同类项”,所以s=3或4
或5,t=1或2或3.
因为t=2k,所以k= 或1或 .
因为s=|x-1|+k,所以|x-1|=s-k.
当s取最大值,k取最小值时,|x-1|取得最
大值,此时x有最大值和最小值,
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
即当s=5,k= 时,|x-1|取得最大值 ,
此时x= 或- ,
所以x的最大值是 ,最小值是- .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
