5.2 等式的基本性质 课件(共31张PPT)
文档属性
| 名称 | 5.2 等式的基本性质 课件(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 12:11:15 | ||
图片预览










文档简介
(共31张PPT)
5.2 等式的基本性质
第5章 一元一次方程
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
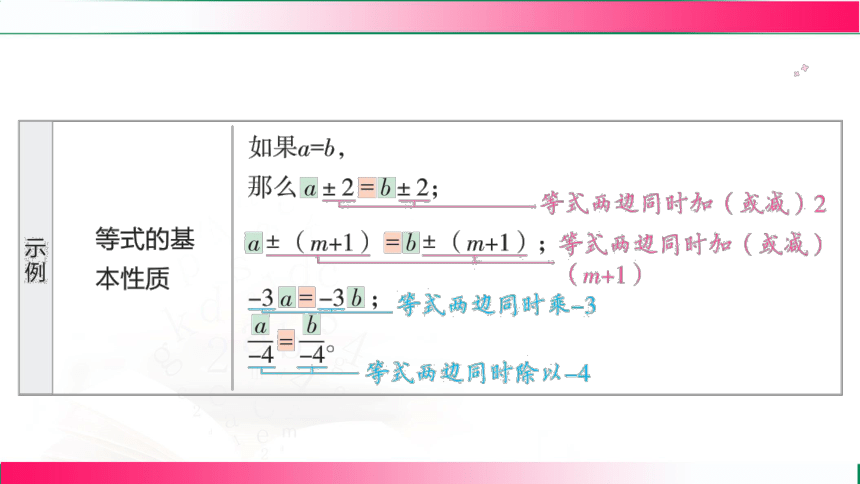
等式的基本性质
课程目标
理解并掌握等式的两条基本性质。
能运用等式的基本性质对等式进行变形。
学会利用等式的基本性质解简单的方程。
体会等式基本性质在解决实际问题中的作用。
等式的基本性质 1
等式两边同时加上(或减去)同一个整式,所得结果仍是等式。
用字母表示为:如果\(a = b\),那么\(a + c = b + c\),\(a - c = b - c\)(其中\(c\)为任意整式)。
实例说明:
若\(x = 5\),在等式两边同时加上 3,得到\(x + 3 = 5 + 3\),即\(x + 3 = 8\),等式仍然成立。
若\(2m + 3 = n\),在等式两边同时减去\(2m\),得到\(2m + 3 - 2m = n - 2m\),即\(3 = n - 2m\),等式依然成立。
生活实例:天平两边各放有质量相等的物体,此时天平平衡(即等式成立)。如果在天平两边同时加上相同质量的砝码,天平仍然保持平衡,这直观地体现了等式的基本性质 1。
等式的基本性质 2
等式两边同时乘(或除以)同一个不为 0 的整式,所得结果仍是等式。
用字母表示为:如果\(a = b\),那么\(ac = bc\);如果\(a = b\)(\(c\neq0\)),那么\(\frac{a}{c}=\frac{b}{c}\)(其中\(c\)为任意不为 0 的整式)。
实例说明:
若\(y = 4\),在等式两边同时乘 2,得到\(2y = 4\times2\),即\(2y = 8\),等式成立。
若\(6x = 18\),在等式两边同时除以 3(3 不为 0),得到\(\frac{6x}{3}=\frac{18}{3}\),即\(2x = 6\),等式成立。
特别注意:等式两边同时除以一个数时,这个数不能为 0。因为 0 不能作为除数,否则无意义。例如,若\(3 = 3\),若两边同时除以 0,式子就变得无意义了,所以这种情况不允许出现。
生活实例:天平两边平衡时,若将两边物体的质量同时扩大相同的倍数(或缩小到原来的几分之一,且不为 0),天平仍然保持平衡,这体现了等式的基本性质 2。
等式基本性质的应用
利用性质变形等式
根据等式的基本性质,可以对等式进行各种合理变形,以满足解决问题的需求。
例如,对等式\(3x - 5 = 7\)进行变形:
利用性质 1,两边同时加上 5,得到\(3x - 5 + 5 = 7 + 5\),即\(3x = 12\)。
再利用性质 2,两边同时除以 3,得到\(\frac{3x}{3}=\frac{12}{3}\),即\(x = 4\)。
利用性质解简单方程
解方程的过程,其实就是利用等式的基本性质把方程逐步变形为\(x = a\)(\(a\)为常数)的形式。
例 1:解方程\(x - 6 = 10\)
根据等式基本性质 1,两边同时加上 6,得\(x - 6 + 6 = 10 + 6\),即\(x = 16\)。
例 2:解方程\(5x = 35\)
根据等式基本性质 2,两边同时除以 5,得\(\frac{5x}{5}=\frac{35}{5}\),即\(x = 7\)。
例 3:解方程\(2x + 3 = 11\)
第一步,根据等式基本性质 1,两边同时减去 3,得\(2x + 3 - 3 = 11 - 3\),即\(2x = 8\)。
第二步,根据等式基本性质 2,两边同时除以 2,得\(\frac{2x}{2}=\frac{8}{2}\),即\(x = 4\)。
等式基本性质的注意事项
运用性质 1 时,两边加上(或减去)的必须是同一个整式,否则等式可能不成立。例如,若\(a = b\),左边加 2,右边加 3,得到\(a + 2\neq b + 3\)。
运用性质 2 时,要注意两点:
两边乘(或除以)的是同一个整式。
除以的这个整式不能为 0,因为 0 做除数无意义。
等式变形时,要保持等式两边的平衡,每一步变形都要严格依据等式的基本性质,不能随意进行操作。
等式基本性质与方程的联系
等式的基本性质是解方程的理论依据。通过运用等式的基本性质,我们可以把方程中的未知数逐步分离出来,最终求出方程的解。例如,对于方程\(4x - 7 = 9\),利用性质 1 两边加 7 得到\(4x = 16\),再利用性质 2 两边除以 4 得到\(x = 4\),整个过程都是以等式的基本性质为基础的。
课堂练习
利用等式的基本性质填空:
若\(m = n\),则\(m + 4 = n +\)( )。
若\(2x = 6y\),则\(x = \)( )(根据性质 2,两边同时除以 2)。
若\(a - 5 = b - 5\),则\(a = \)( )(根据性质 1,两边同时加上 5)。
利用等式的基本性质解下列方程:
\(x + 8 = 15\)
\(3x = 24\)
\(2x - 5 = 13\)
判断下列变形是否正确,并说明理由:
由\(5x = 4x + 3\),得\(5x - 4x = 3\)。
由\(7x = 8\),得\(x = \frac{7}{8}\)。
总结
等式的基本性质 1:两边同时加上(或减去)同一个整式,结果仍是等式。
等式的基本性质 2:两边同时乘(或除以)同一个不为 0 的整式,结果仍是等式。
等式的基本性质是解方程的重要依据,运用时要注意相关事项,确保变形正确。
掌握等式的基本性质,能帮助我们更好地处理等式变形和解决方程问题,为后续学习更复杂的方程奠定基础。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.借助天平理解并掌握等式的基本性质。
2.能利用等式的基本性质进行等式的变形。
3.能利用等式的基本性质解方程,体会化归思想。
内容 字母表示
等式的 性质1 等式的两边都加上(或都减去) 同一个数或式,所得结果仍是等 式。
等式的 性质2 等式的两边都乘或都除以同一个 数或式(除数不能为零),所得 结果仍是等式。
教材延伸
等式的其他性质
(1)等式的对称性:如果,那么 。
(2)等式的传递性:如果,,那么 。
典例1 (易错题)下列变形中,不正确的是( )
D
A.若,则 B.若,则
C.若,则 D.若,则
解析:
选项 变形形式 分析 结论
A 两边同时加3。 符合等式的性质1。 正确
B 符合等式的性质2。 正确
C 符合等式的性质2。 正确
D 不正确
知识过关
①等式的两边都 加上 (或都 减去 )同一个 数或式 ,
所得结果仍是等式.用字母可以表示为: 如果a=b,那么
a±c=b±c .
②等式的两边都 乘 或都 除以 同一个 数或式(除数不
能为零) ,所得结果仍是等式.用字母可以表示为: 如果
a=b,那么ac=bc或 = (c≠0) .
加上
减去
数或式
如果a=b,那么
a±c=b±c
乘
除以
数或式(除数不
能为零)
如果
a=b,那么ac=bc或 = (c≠0)
等式的基本性质
1. 根据等式的性质,下列各式变形不正确的是( D )
A. 若x=y,则x+3=y+3
B. 若-2x=-2y,则x=y
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. [2024·金华期末]已知等式a=b,则下列等式中不一定成
立的是( B )
A. a-c=b-c
C. an=bn D. a2=b2
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
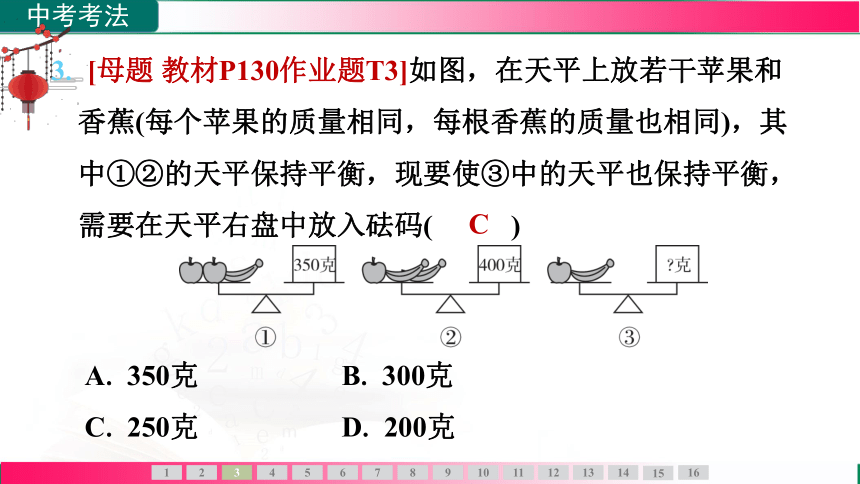
3. [母题 教材P130作业题T3]如图,在天平上放若干苹果和
香蕉(每个苹果的质量相同,每根香蕉的质量也相同),其
中①②的天平保持平衡,现要使③中的天平也保持平衡,
需要在天平右盘中放入砝码( C )
A. 350克 B. 300克
C. 250克 D. 200克
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. 把方程 x=1变形为x=3,其依据是( C )
A. 分数的基本性质 B. 等式的基本性质1
C. 等式的基本性质2 D. 以上都不对
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5. 如果a=b,那么 = 成立时c应满足的条件
是 .
c≠1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
利用等式的基本性质解方程
6. 下列过程正确的是( C )
A. 从12-2x=-6,得到12-6=2x
B. 从-8x+4=-5x-2,得到8x+5x=-4-2
C. 从5x+3=4x+2,得到5x-2=4x-3
D. 从-3x-4=2x-8,得到8-4=2x-3x
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 在方程4x-3=5的两边都 ,得到4x=8,这是
根据 ;在方程-2x= 的两边都
,得到x=- ,这是根据 .
8. 若x=2是关于x的方程2x+3m-1=0的解,则m的值
为 .
加上3
等式的性质1
除以
-2
等式的性质2
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1) x=-12;
(2)3-2x=9;
【解】x=-16;
【解】x=-3;
9. 利用等式的性质解下列方程:
(3)4x+8=-14x;
(4)3- x= .
【解】x=- ;
【解】x= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. 根据等式的性质,下列变形正确的是( A )
B. 若ac=bc,则a=b
C. 若a2=b2,则a=b
A
[易错题]忽视除式不为零而错用等式的基本性质
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. [2024·嘉兴期末]已知m-n=0,且m-a=n+b,则
a,b一定满足的关系式是( D )
A. ab=0 B. ab=1
C. a-b=0 D. a+b=0
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 若a,b,c,m都是有理数,并且a+2b+3c=m,
a+b+2c=m,则b与c( C )
A. 互为倒数 B. 互为负倒数
C. 互为相反数 D. 相等
C
13. 在等式4x-7=3x+5的两边同时减去一个多项式可以
得到等式x=12,则这个多项式是 .
3x-7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. [新趋势·过程性学习]有一个爱思考的同学,有一天他对
妈妈说:“我发现2和5是可以一样大的,我这里有一个
方程5x-2=2x-2.方程两边同时加2,得5x-2+2=
2x-2+2①,即5x=2x.方程两边同时除以x,得5=2
②.”你认为这个同学的说法正确吗?如果正确,请说明
上述①②步的理由;如果不正确,请指出错在哪里,并
加以改正.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】不正确,解5x=2x时不能给方程的两边同时除
以x,正确过程如下:
5x-2=2x-2,
方程两边同时加2,得5x=2x,
方程两边同时减去2x,得3x=0,
方程两边同时除以3,得x=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. 已知t= (a,b是常数,x≠-a)①.
(1)若a=-2,b= ,求t;
【解】当a=-2,b= 时,
t= = = ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)试将等式①变形成“Ax=B”的形式,其中A,B表
示关于a,b,t的整式;
【解】将t= 两边都乘以(x+a),得
tx+ta=bx-1,
两边都减去(ta+bx),得tx-bx=-1-ta,
两边都乘以-1,得bx-tx=ta+1,
即(b-t)x=ta+1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)若t的取值与x无关,请说明ab=-1.
【解】因为t的取值与x无关,
所以b-t=0,即b=t,
ta+1=0,即ab+1=0,
所以ab=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16. [新考法·阅读类比法]阅读下列材料:
问题:怎样将0. 表示成分数的形式?
小明的探究过程如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
根据以上信息,回答下列问题:
(1)从步骤①到步骤②,变形的依据是 ,从
步骤⑤到步骤⑥,变形的依据是 .
等式的性质2
等式的性质1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)仿照上述探究过程,请你将0. 表示成分数的形式.
【解】设x=0. ,
两边同时乘以10,得10x=10×0. ,
则10x=3. ,即10x=3+0. ,
所以10x=3+x,
两边同时减去x,得9x=3,
两边同时除以9,x= ,即0. = .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看!
5.2 等式的基本性质
第5章 一元一次方程
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
等式的基本性质
课程目标
理解并掌握等式的两条基本性质。
能运用等式的基本性质对等式进行变形。
学会利用等式的基本性质解简单的方程。
体会等式基本性质在解决实际问题中的作用。
等式的基本性质 1
等式两边同时加上(或减去)同一个整式,所得结果仍是等式。
用字母表示为:如果\(a = b\),那么\(a + c = b + c\),\(a - c = b - c\)(其中\(c\)为任意整式)。
实例说明:
若\(x = 5\),在等式两边同时加上 3,得到\(x + 3 = 5 + 3\),即\(x + 3 = 8\),等式仍然成立。
若\(2m + 3 = n\),在等式两边同时减去\(2m\),得到\(2m + 3 - 2m = n - 2m\),即\(3 = n - 2m\),等式依然成立。
生活实例:天平两边各放有质量相等的物体,此时天平平衡(即等式成立)。如果在天平两边同时加上相同质量的砝码,天平仍然保持平衡,这直观地体现了等式的基本性质 1。
等式的基本性质 2
等式两边同时乘(或除以)同一个不为 0 的整式,所得结果仍是等式。
用字母表示为:如果\(a = b\),那么\(ac = bc\);如果\(a = b\)(\(c\neq0\)),那么\(\frac{a}{c}=\frac{b}{c}\)(其中\(c\)为任意不为 0 的整式)。
实例说明:
若\(y = 4\),在等式两边同时乘 2,得到\(2y = 4\times2\),即\(2y = 8\),等式成立。
若\(6x = 18\),在等式两边同时除以 3(3 不为 0),得到\(\frac{6x}{3}=\frac{18}{3}\),即\(2x = 6\),等式成立。
特别注意:等式两边同时除以一个数时,这个数不能为 0。因为 0 不能作为除数,否则无意义。例如,若\(3 = 3\),若两边同时除以 0,式子就变得无意义了,所以这种情况不允许出现。
生活实例:天平两边平衡时,若将两边物体的质量同时扩大相同的倍数(或缩小到原来的几分之一,且不为 0),天平仍然保持平衡,这体现了等式的基本性质 2。
等式基本性质的应用
利用性质变形等式
根据等式的基本性质,可以对等式进行各种合理变形,以满足解决问题的需求。
例如,对等式\(3x - 5 = 7\)进行变形:
利用性质 1,两边同时加上 5,得到\(3x - 5 + 5 = 7 + 5\),即\(3x = 12\)。
再利用性质 2,两边同时除以 3,得到\(\frac{3x}{3}=\frac{12}{3}\),即\(x = 4\)。
利用性质解简单方程
解方程的过程,其实就是利用等式的基本性质把方程逐步变形为\(x = a\)(\(a\)为常数)的形式。
例 1:解方程\(x - 6 = 10\)
根据等式基本性质 1,两边同时加上 6,得\(x - 6 + 6 = 10 + 6\),即\(x = 16\)。
例 2:解方程\(5x = 35\)
根据等式基本性质 2,两边同时除以 5,得\(\frac{5x}{5}=\frac{35}{5}\),即\(x = 7\)。
例 3:解方程\(2x + 3 = 11\)
第一步,根据等式基本性质 1,两边同时减去 3,得\(2x + 3 - 3 = 11 - 3\),即\(2x = 8\)。
第二步,根据等式基本性质 2,两边同时除以 2,得\(\frac{2x}{2}=\frac{8}{2}\),即\(x = 4\)。
等式基本性质的注意事项
运用性质 1 时,两边加上(或减去)的必须是同一个整式,否则等式可能不成立。例如,若\(a = b\),左边加 2,右边加 3,得到\(a + 2\neq b + 3\)。
运用性质 2 时,要注意两点:
两边乘(或除以)的是同一个整式。
除以的这个整式不能为 0,因为 0 做除数无意义。
等式变形时,要保持等式两边的平衡,每一步变形都要严格依据等式的基本性质,不能随意进行操作。
等式基本性质与方程的联系
等式的基本性质是解方程的理论依据。通过运用等式的基本性质,我们可以把方程中的未知数逐步分离出来,最终求出方程的解。例如,对于方程\(4x - 7 = 9\),利用性质 1 两边加 7 得到\(4x = 16\),再利用性质 2 两边除以 4 得到\(x = 4\),整个过程都是以等式的基本性质为基础的。
课堂练习
利用等式的基本性质填空:
若\(m = n\),则\(m + 4 = n +\)( )。
若\(2x = 6y\),则\(x = \)( )(根据性质 2,两边同时除以 2)。
若\(a - 5 = b - 5\),则\(a = \)( )(根据性质 1,两边同时加上 5)。
利用等式的基本性质解下列方程:
\(x + 8 = 15\)
\(3x = 24\)
\(2x - 5 = 13\)
判断下列变形是否正确,并说明理由:
由\(5x = 4x + 3\),得\(5x - 4x = 3\)。
由\(7x = 8\),得\(x = \frac{7}{8}\)。
总结
等式的基本性质 1:两边同时加上(或减去)同一个整式,结果仍是等式。
等式的基本性质 2:两边同时乘(或除以)同一个不为 0 的整式,结果仍是等式。
等式的基本性质是解方程的重要依据,运用时要注意相关事项,确保变形正确。
掌握等式的基本性质,能帮助我们更好地处理等式变形和解决方程问题,为后续学习更复杂的方程奠定基础。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.借助天平理解并掌握等式的基本性质。
2.能利用等式的基本性质进行等式的变形。
3.能利用等式的基本性质解方程,体会化归思想。
内容 字母表示
等式的 性质1 等式的两边都加上(或都减去) 同一个数或式,所得结果仍是等 式。
等式的 性质2 等式的两边都乘或都除以同一个 数或式(除数不能为零),所得 结果仍是等式。
教材延伸
等式的其他性质
(1)等式的对称性:如果,那么 。
(2)等式的传递性:如果,,那么 。
典例1 (易错题)下列变形中,不正确的是( )
D
A.若,则 B.若,则
C.若,则 D.若,则
解析:
选项 变形形式 分析 结论
A 两边同时加3。 符合等式的性质1。 正确
B 符合等式的性质2。 正确
C 符合等式的性质2。 正确
D 不正确
知识过关
①等式的两边都 加上 (或都 减去 )同一个 数或式 ,
所得结果仍是等式.用字母可以表示为: 如果a=b,那么
a±c=b±c .
②等式的两边都 乘 或都 除以 同一个 数或式(除数不
能为零) ,所得结果仍是等式.用字母可以表示为: 如果
a=b,那么ac=bc或 = (c≠0) .
加上
减去
数或式
如果a=b,那么
a±c=b±c
乘
除以
数或式(除数不
能为零)
如果
a=b,那么ac=bc或 = (c≠0)
等式的基本性质
1. 根据等式的性质,下列各式变形不正确的是( D )
A. 若x=y,则x+3=y+3
B. 若-2x=-2y,则x=y
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. [2024·金华期末]已知等式a=b,则下列等式中不一定成
立的是( B )
A. a-c=b-c
C. an=bn D. a2=b2
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3. [母题 教材P130作业题T3]如图,在天平上放若干苹果和
香蕉(每个苹果的质量相同,每根香蕉的质量也相同),其
中①②的天平保持平衡,现要使③中的天平也保持平衡,
需要在天平右盘中放入砝码( C )
A. 350克 B. 300克
C. 250克 D. 200克
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. 把方程 x=1变形为x=3,其依据是( C )
A. 分数的基本性质 B. 等式的基本性质1
C. 等式的基本性质2 D. 以上都不对
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5. 如果a=b,那么 = 成立时c应满足的条件
是 .
c≠1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
利用等式的基本性质解方程
6. 下列过程正确的是( C )
A. 从12-2x=-6,得到12-6=2x
B. 从-8x+4=-5x-2,得到8x+5x=-4-2
C. 从5x+3=4x+2,得到5x-2=4x-3
D. 从-3x-4=2x-8,得到8-4=2x-3x
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 在方程4x-3=5的两边都 ,得到4x=8,这是
根据 ;在方程-2x= 的两边都
,得到x=- ,这是根据 .
8. 若x=2是关于x的方程2x+3m-1=0的解,则m的值
为 .
加上3
等式的性质1
除以
-2
等式的性质2
-1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1) x=-12;
(2)3-2x=9;
【解】x=-16;
【解】x=-3;
9. 利用等式的性质解下列方程:
(3)4x+8=-14x;
(4)3- x= .
【解】x=- ;
【解】x= .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. 根据等式的性质,下列变形正确的是( A )
B. 若ac=bc,则a=b
C. 若a2=b2,则a=b
A
[易错题]忽视除式不为零而错用等式的基本性质
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. [2024·嘉兴期末]已知m-n=0,且m-a=n+b,则
a,b一定满足的关系式是( D )
A. ab=0 B. ab=1
C. a-b=0 D. a+b=0
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 若a,b,c,m都是有理数,并且a+2b+3c=m,
a+b+2c=m,则b与c( C )
A. 互为倒数 B. 互为负倒数
C. 互为相反数 D. 相等
C
13. 在等式4x-7=3x+5的两边同时减去一个多项式可以
得到等式x=12,则这个多项式是 .
3x-7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. [新趋势·过程性学习]有一个爱思考的同学,有一天他对
妈妈说:“我发现2和5是可以一样大的,我这里有一个
方程5x-2=2x-2.方程两边同时加2,得5x-2+2=
2x-2+2①,即5x=2x.方程两边同时除以x,得5=2
②.”你认为这个同学的说法正确吗?如果正确,请说明
上述①②步的理由;如果不正确,请指出错在哪里,并
加以改正.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】不正确,解5x=2x时不能给方程的两边同时除
以x,正确过程如下:
5x-2=2x-2,
方程两边同时加2,得5x=2x,
方程两边同时减去2x,得3x=0,
方程两边同时除以3,得x=0.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. 已知t= (a,b是常数,x≠-a)①.
(1)若a=-2,b= ,求t;
【解】当a=-2,b= 时,
t= = = ;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)试将等式①变形成“Ax=B”的形式,其中A,B表
示关于a,b,t的整式;
【解】将t= 两边都乘以(x+a),得
tx+ta=bx-1,
两边都减去(ta+bx),得tx-bx=-1-ta,
两边都乘以-1,得bx-tx=ta+1,
即(b-t)x=ta+1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)若t的取值与x无关,请说明ab=-1.
【解】因为t的取值与x无关,
所以b-t=0,即b=t,
ta+1=0,即ab+1=0,
所以ab=-1.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
16. [新考法·阅读类比法]阅读下列材料:
问题:怎样将0. 表示成分数的形式?
小明的探究过程如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
根据以上信息,回答下列问题:
(1)从步骤①到步骤②,变形的依据是 ,从
步骤⑤到步骤⑥,变形的依据是 .
等式的性质2
等式的性质1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)仿照上述探究过程,请你将0. 表示成分数的形式.
【解】设x=0. ,
两边同时乘以10,得10x=10×0. ,
则10x=3. ,即10x=3+0. ,
所以10x=3+x,
两边同时减去x,得9x=3,
两边同时除以9,x= ,即0. = .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
