6.1 几何图形 课件(共34张PPT)
文档属性
| 名称 | 6.1 几何图形 课件(共34张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 12:15:09 | ||
图片预览










文档简介
(共34张PPT)
6.1 几何图形
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
几何图形
课程目标
理解几何图形的概念,能区分立体图形和平面图形。
掌握立体图形和平面图形的特点,了解它们之间的联系与区别。
认识常见的几何图形,能说出它们的名称和基本特征。
感受几何图形在生活中的广泛应用,培养空间想象能力。
几何图形的定义
我们生活的世界充满了各种各样的物体,这些物体都具有形状、大小和位置关系。从实物中抽象出来的各种图形,统称为几何图形。几何图形是数学研究的重要对象之一,它忽略了实物的颜色、材料等非本质属性,只关注其形状、大小和位置。
例如:我们看到的足球可以抽象成球体,黑板可以抽象成长方形,金字塔可以抽象成棱锥等。
几何图形的分类
几何图形按照其是否在同一平面内,可分为立体图形和平面图形。
立体图形
定义:各部分不都在同一平面内的几何图形叫做立体图形,也称为空间图形。
特点:具有三维空间结构,即具有长度、宽度和高度,能占据一定的空间。
常见的立体图形:
球体:由一个曲面围成的封闭图形,从任何方向看都是圆形,如足球、篮球。
柱体:包括圆柱和棱柱。
圆柱:由两个大小相等、互相平行的圆形底面和一个曲面侧面围成,如罐头、水桶。
棱柱:有两个互相平行且全等的多边形底面,侧面是长方形,底面是几边形就叫做几棱柱,如三棱柱(底面是三角形)、四棱柱(底面是四边形,像长方体、正方体)。
锥体:包括圆锥和棱锥。
圆锥:由一个圆形底面和一个曲面侧面围成,侧面展开是扇形,如烟囱帽、圣诞帽。
棱锥:有一个多边形底面,侧面是三角形,底面是几边形就叫做几棱锥,如三棱锥、四棱锥(像金字塔)。
平面图形
定义:各部分都在同一平面内的几何图形叫做平面图形。
特点:只具有二维空间结构,即只有长度和宽度,没有高度,不能占据空间,只能在一个平面内表现。
常见的平面图形:
多边形:由线段首尾顺次相接围成的封闭图形,如三角形(由 3 条线段围成)、四边形(由 4 条线段围成,包括长方形、正方形、平行四边形、梯形等)、五边形等。
圆:由一条曲线围成的封闭图形,没有顶点和边,如硬币的表面、钟表的表盘。
其他平面图形:如线段、射线、直线等。
立体图形与平面图形的关系
联系:
立体图形是由平面图形组成的。例如,长方体是由 6 个长方形(特殊情况下有 2 个正方形)组成的;圆柱的两个底面是圆形。
将立体图形的表面适当展开,可以得到平面图形,这个平面图形叫做该立体图形的展开图。例如,正方体的表面展开图是由 6 个正方形组成的;圆柱的侧面展开图是一个长方形。
平面图形可以通过折叠等方式形成立体图形。例如,将一个长方形纸卷起来可以形成一个圆柱;将正方体的展开图折叠可以得到正方体。
区别:
立体图形具有三维空间结构(长、宽、高),能占据空间;平面图形具有二维空间结构(长、宽),不能占据空间,只存在于平面内。
生活中的几何图形
几何图形在我们的生活中无处不在:
建筑方面:房屋的外形可能是长方体,屋顶可能是三棱柱或圆锥;桥梁的结构中包含三角形(具有稳定性)、平行四边形等。
日常用品:书本的封面是长方形,魔方是正方体,易拉罐是圆柱,车轮是圆形。
艺术设计:许多图案的设计都运用了平面图形,如三角形、圆形的组合;雕塑作品则多为立体图形。
从实物中抽象出几何图形的方法
观察实物的形状,忽略其颜色、材质、图案等次要属性。
找到实物最基本的几何特征,将其与学过的几何图形联系起来。
用简洁的几何语言描述抽象出的图形。
例如:观察一个粉笔盒,忽略其颜色和上面的文字,它的形状是长方体,所以可以抽象成长方体这个立体图形;观察一个钟面,忽略其刻度和指针,它的形状是圆形,所以可以抽象成圆形这个平面图形。
课堂练习
指出下列物体对应的立体图形名称:
篮球
魔方
金字塔
罐头
下列图形中,哪些是平面图形,哪些是立体图形?
三角形
圆柱
正方形
圆锥
圆
说出正方体有几个面,每个面是什么形状;圆柱有几个面,分别是什么形状。
总结
几何图形是从实物中抽象出来的,分为立体图形和平面图形。
立体图形各部分不都在同一平面内,具有长、宽、高,常见的有球体、柱体、锥体等;平面图形各部分都在同一平面内,只有长和宽,常见的有多边形、圆等。
立体图形和平面图形相互联系,立体图形可展开为平面图形,平面图形可折叠成立体图形。
生活中充满了几何图形,学会从实物中抽象出几何图形,有助于我们更好地理解和运用几何知识。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.通过实物和模型,了解从物体外形中抽象出来的点、线、
面、体。
2.知道立体图形与平面图形的特征和关系,能识别立体图形
和平面图形,发展空间观念。
3.理解点、线、面、体之间的关系,掌握怎样由平面图形旋
转得到几何体形成空间观念。
4.能用七巧板拼出不同图案,提高动手操作能力。
1.定义:点、线、面、体称为几何图形。
几何图形是从实物中抽象得到的,只注重物体的形状、
大小、位置,而不注重它的其他属性,如质量,颜色等。
2.分类:
定义 举例
立体 图形 图形所表示的各个部分不在同一个 平面内,这样的几何图形称为立体 图形。 长方体,圆柱,圆
锥,球等。
平面 图形 图形所表示的各个部分都在同一个 平面内,称为平面图形。 如线段、角、三角
形、圆等。
教材延伸
常见的立体图形的分类方法
(1)
(2)
圆柱与棱柱的相同点与不同点
相同点 不同点 底面形状 侧面 顶点 棱
圆柱 都有两个互相 平行且形状和 大小完全相同 的底面。 圆 一个 曲面 无顶点 无
棱柱 多边形 平行四 边形 有顶点 有多条
典例1 如图,请写出下列实物的形状对应的立体图形名称。
解:图中(1)(2)(3)(4)(5)对应的立体图形分别是
球、圆柱、长方体(或四棱柱)、圆锥、棱锥。
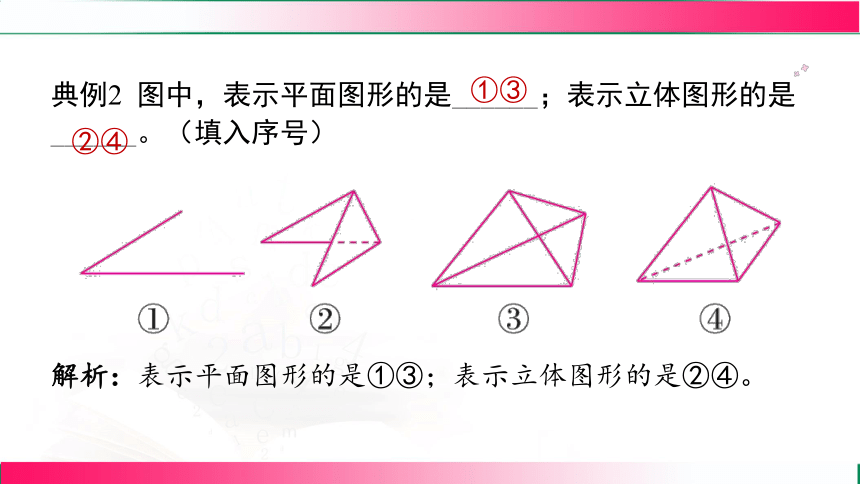
典例2 图中,表示平面图形的是______;表示立体图形的是
______。(填入序号)
①③
②④
解析:表示平面图形的是①③;表示立体图形的是②④。
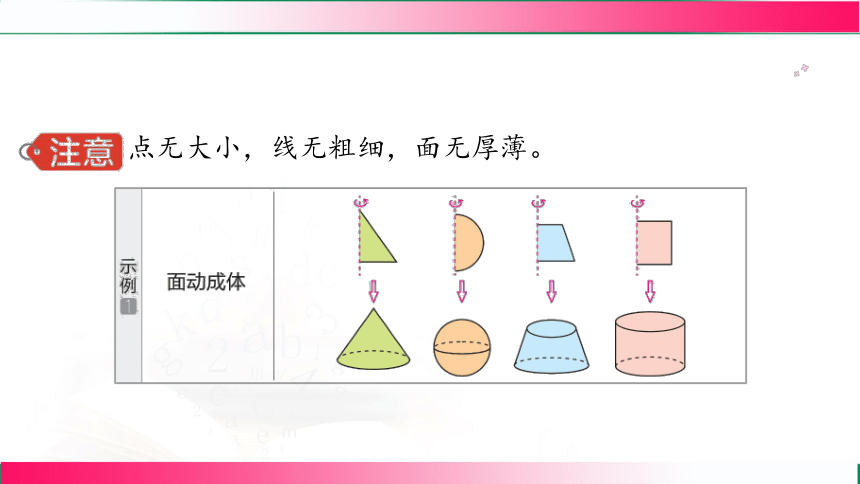
1.图形的构成元素:图形是由点、线、面构成的。
2.元素之间的关系
点无大小,线无粗细,面无厚薄。
七巧板:七巧板又称“七巧图”“智慧板”,是中国古老的智力
玩具。如图,七巧板由七块板组成,完整图案为一个正方形,
由七块板可以变换出各种不同的图案。
知识过关
①从实物中得到的 点 、 线 、 面 、 体 称为几何图形.
②图形所表示的各个部分 不在 同一个平面内,这样的几何图形称为立体图形;图形所表示的各个部分 都在 同一个平面内,称为平面图形.
点
线
面
体
不在
都在
认识几何图形
1. 如图中的几何图形从左到右依次是( B )
A. 长方形,圆,正方形,三角形
B. 圆柱,球,长方体,棱锥
C. 圆柱,球,长方体,圆锥
D. 长方体,球,棱锥,棱柱
B
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图所示的是一座房子的平面图,组成这幅图的几何图形
有( C )
A. 三角形、长方形
B. 三角形、正方形、长方形
C. 三角形、长方形、梯形
D. 正方形、长方形、梯形
C
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 把下列几何图形分别填到下面的括号里.
圆,圆柱,球,扇形,等腰三角形,长方体,正方
体,直角.
立体图形:{ …};
平面图形:{ …}.
圆柱,球,长方体,正方体
圆,扇形,等腰三角形,直角
1
2
3
4
5
6
7
8
9
10
11
12
13
几何体中的顶点、棱、面
4. 如图,几何体圆锥的面数是( B )
A. 1
B. 2
C. 3
D. 4
B
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图所示的五棱柱的底面边长都是5 cm,侧棱长12 cm,
它有多少个面?它有多少条棱?它有多少个顶点?它的所
有侧面的面积之和是多少?
【解】它有7个面,15条棱,10个顶点.
它的所有侧面的面积之和为5×12×5=300(cm2).
1
2
3
4
5
6
7
8
9
10
11
12
13
点、线、面、体的关系
6. [2024·杭州下沙期中]汽车的雨刷把玻璃上的雨雪刷干净属
于以下哪项几何知识的实际应用( B )
A. 点动成线 B. 线动成面
C. 面动成体 D. 以上答案都正确
B
1
2
3
4
5
6
7
8
9
10
11
12
13
7. [新趋势·跨学科]在朱自清的《春》中描写春雨“像牛毛,
像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨
看成了线,这说明了 .
点动成线
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 图中图形绕直线l旋转一周后,会得到什么立体图形?用
线连一连.
1
2
3
4
5
6
7
8
9
10
11
12
13
[易错题]对旋转后的几何图形考虑不全面而出错
9. 直角三角形的两条直角边的长分别为8 cm,6 cm,以其中
一条直角边所在直线为轴旋转一周,得到的几何体的底面
积是多少?(结果保留π)
【解】由题意知,以其中一条直角边所在直线为轴旋转一
周所得几何体为圆锥,底面是圆,底面半径是8 cm或6 cm,所以底面积是64π cm2或36π cm2.
1
2
3
4
5
6
7
8
9
10
11
12
13
10. [2024·温州龙湾区模拟]不透明袋子中装有一个几何体模
型,两名同学摸该模型并描述它的特征,甲同学:它有4
个面是三角形;乙同学:它有6条棱.则该模型对应的立
体图形可能是( C )
A. 三棱柱 B. 四棱柱
C. 三棱锥 D. 四棱锥
C
1
2
3
4
5
6
7
8
9
10
11
12
13
11. [立德树人·传统文化]七巧板是我们祖先的一项卓越创
造,被西方人誉为“东方魔板”.如图是一副正方形七巧
板(相同的板规定序号相同).现从七巧板中取出四块(序号
可以相同)拼成一个小正方形(无空隙不重叠),则可以拼
成的序号是( B )
A. ②③③④
B. ①①②③
C. ①①②④
D. ①①②⑤
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
由题意可知,①①②③四块板可拼成一个小正方形
(无空隙不重叠),如图:
故选:B.
B
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图①是三个形状完全相同的几何体(下底面为圆,单
位:厘米),将它们拼成如图②的新几何体,求该新几何
体的体积.(结果保留π)
1
2
3
4
5
6
7
8
9
10
11
12
13
【解】π×(4÷2)2×(4+6)+ [π×(4÷2)2×(4+6)]=40π
+20π=60π(立方厘米).
答:该新几何体的体积为60π立方厘米.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [新视角·规律探究题]简单多面体是各个面都是多边形组
成的几何体,十八世纪瑞士数学家欧拉证明了简单多面
体中顶点数(V)、面数(F)和棱数(E)之间存在一个有趣的
关系式,称为欧拉公式.如表是根据下面的多面体模型列
出的不完整的表:
1
2
3
4
5
6
7
8
9
10
11
12
13
多面体 顶点数 面数 棱数
四面体 4 4 6
长方体 8 6
正八面体 8 12
1
2
3
4
5
6
7
8
9
10
11
12
13
现在有一个多面体,它的每一个面都是三角形,它的面
数(F)和棱数(E)的和为30,则这个多面体的顶点数V
= .
8
1
2
3
4
5
6
7
8
9
10
11
12
13
由表可知这个多面体的顶点数V=2+E-F.
因为有一个多面体,每一个面都是三角形,
所以每相邻两条边重合为一条棱,
所以E= F.
因为E+F=30,所以F=12,所以E=18,
所以V=2+E-F=8.
故答案为8.
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
6.1 几何图形
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
几何图形
课程目标
理解几何图形的概念,能区分立体图形和平面图形。
掌握立体图形和平面图形的特点,了解它们之间的联系与区别。
认识常见的几何图形,能说出它们的名称和基本特征。
感受几何图形在生活中的广泛应用,培养空间想象能力。
几何图形的定义
我们生活的世界充满了各种各样的物体,这些物体都具有形状、大小和位置关系。从实物中抽象出来的各种图形,统称为几何图形。几何图形是数学研究的重要对象之一,它忽略了实物的颜色、材料等非本质属性,只关注其形状、大小和位置。
例如:我们看到的足球可以抽象成球体,黑板可以抽象成长方形,金字塔可以抽象成棱锥等。
几何图形的分类
几何图形按照其是否在同一平面内,可分为立体图形和平面图形。
立体图形
定义:各部分不都在同一平面内的几何图形叫做立体图形,也称为空间图形。
特点:具有三维空间结构,即具有长度、宽度和高度,能占据一定的空间。
常见的立体图形:
球体:由一个曲面围成的封闭图形,从任何方向看都是圆形,如足球、篮球。
柱体:包括圆柱和棱柱。
圆柱:由两个大小相等、互相平行的圆形底面和一个曲面侧面围成,如罐头、水桶。
棱柱:有两个互相平行且全等的多边形底面,侧面是长方形,底面是几边形就叫做几棱柱,如三棱柱(底面是三角形)、四棱柱(底面是四边形,像长方体、正方体)。
锥体:包括圆锥和棱锥。
圆锥:由一个圆形底面和一个曲面侧面围成,侧面展开是扇形,如烟囱帽、圣诞帽。
棱锥:有一个多边形底面,侧面是三角形,底面是几边形就叫做几棱锥,如三棱锥、四棱锥(像金字塔)。
平面图形
定义:各部分都在同一平面内的几何图形叫做平面图形。
特点:只具有二维空间结构,即只有长度和宽度,没有高度,不能占据空间,只能在一个平面内表现。
常见的平面图形:
多边形:由线段首尾顺次相接围成的封闭图形,如三角形(由 3 条线段围成)、四边形(由 4 条线段围成,包括长方形、正方形、平行四边形、梯形等)、五边形等。
圆:由一条曲线围成的封闭图形,没有顶点和边,如硬币的表面、钟表的表盘。
其他平面图形:如线段、射线、直线等。
立体图形与平面图形的关系
联系:
立体图形是由平面图形组成的。例如,长方体是由 6 个长方形(特殊情况下有 2 个正方形)组成的;圆柱的两个底面是圆形。
将立体图形的表面适当展开,可以得到平面图形,这个平面图形叫做该立体图形的展开图。例如,正方体的表面展开图是由 6 个正方形组成的;圆柱的侧面展开图是一个长方形。
平面图形可以通过折叠等方式形成立体图形。例如,将一个长方形纸卷起来可以形成一个圆柱;将正方体的展开图折叠可以得到正方体。
区别:
立体图形具有三维空间结构(长、宽、高),能占据空间;平面图形具有二维空间结构(长、宽),不能占据空间,只存在于平面内。
生活中的几何图形
几何图形在我们的生活中无处不在:
建筑方面:房屋的外形可能是长方体,屋顶可能是三棱柱或圆锥;桥梁的结构中包含三角形(具有稳定性)、平行四边形等。
日常用品:书本的封面是长方形,魔方是正方体,易拉罐是圆柱,车轮是圆形。
艺术设计:许多图案的设计都运用了平面图形,如三角形、圆形的组合;雕塑作品则多为立体图形。
从实物中抽象出几何图形的方法
观察实物的形状,忽略其颜色、材质、图案等次要属性。
找到实物最基本的几何特征,将其与学过的几何图形联系起来。
用简洁的几何语言描述抽象出的图形。
例如:观察一个粉笔盒,忽略其颜色和上面的文字,它的形状是长方体,所以可以抽象成长方体这个立体图形;观察一个钟面,忽略其刻度和指针,它的形状是圆形,所以可以抽象成圆形这个平面图形。
课堂练习
指出下列物体对应的立体图形名称:
篮球
魔方
金字塔
罐头
下列图形中,哪些是平面图形,哪些是立体图形?
三角形
圆柱
正方形
圆锥
圆
说出正方体有几个面,每个面是什么形状;圆柱有几个面,分别是什么形状。
总结
几何图形是从实物中抽象出来的,分为立体图形和平面图形。
立体图形各部分不都在同一平面内,具有长、宽、高,常见的有球体、柱体、锥体等;平面图形各部分都在同一平面内,只有长和宽,常见的有多边形、圆等。
立体图形和平面图形相互联系,立体图形可展开为平面图形,平面图形可折叠成立体图形。
生活中充满了几何图形,学会从实物中抽象出几何图形,有助于我们更好地理解和运用几何知识。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.通过实物和模型,了解从物体外形中抽象出来的点、线、
面、体。
2.知道立体图形与平面图形的特征和关系,能识别立体图形
和平面图形,发展空间观念。
3.理解点、线、面、体之间的关系,掌握怎样由平面图形旋
转得到几何体形成空间观念。
4.能用七巧板拼出不同图案,提高动手操作能力。
1.定义:点、线、面、体称为几何图形。
几何图形是从实物中抽象得到的,只注重物体的形状、
大小、位置,而不注重它的其他属性,如质量,颜色等。
2.分类:
定义 举例
立体 图形 图形所表示的各个部分不在同一个 平面内,这样的几何图形称为立体 图形。 长方体,圆柱,圆
锥,球等。
平面 图形 图形所表示的各个部分都在同一个 平面内,称为平面图形。 如线段、角、三角
形、圆等。
教材延伸
常见的立体图形的分类方法
(1)
(2)
圆柱与棱柱的相同点与不同点
相同点 不同点 底面形状 侧面 顶点 棱
圆柱 都有两个互相 平行且形状和 大小完全相同 的底面。 圆 一个 曲面 无顶点 无
棱柱 多边形 平行四 边形 有顶点 有多条
典例1 如图,请写出下列实物的形状对应的立体图形名称。
解:图中(1)(2)(3)(4)(5)对应的立体图形分别是
球、圆柱、长方体(或四棱柱)、圆锥、棱锥。
典例2 图中,表示平面图形的是______;表示立体图形的是
______。(填入序号)
①③
②④
解析:表示平面图形的是①③;表示立体图形的是②④。
1.图形的构成元素:图形是由点、线、面构成的。
2.元素之间的关系
点无大小,线无粗细,面无厚薄。
七巧板:七巧板又称“七巧图”“智慧板”,是中国古老的智力
玩具。如图,七巧板由七块板组成,完整图案为一个正方形,
由七块板可以变换出各种不同的图案。
知识过关
①从实物中得到的 点 、 线 、 面 、 体 称为几何图形.
②图形所表示的各个部分 不在 同一个平面内,这样的几何图形称为立体图形;图形所表示的各个部分 都在 同一个平面内,称为平面图形.
点
线
面
体
不在
都在
认识几何图形
1. 如图中的几何图形从左到右依次是( B )
A. 长方形,圆,正方形,三角形
B. 圆柱,球,长方体,棱锥
C. 圆柱,球,长方体,圆锥
D. 长方体,球,棱锥,棱柱
B
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图所示的是一座房子的平面图,组成这幅图的几何图形
有( C )
A. 三角形、长方形
B. 三角形、正方形、长方形
C. 三角形、长方形、梯形
D. 正方形、长方形、梯形
C
1
2
3
4
5
6
7
8
9
10
11
12
13
3. 把下列几何图形分别填到下面的括号里.
圆,圆柱,球,扇形,等腰三角形,长方体,正方
体,直角.
立体图形:{ …};
平面图形:{ …}.
圆柱,球,长方体,正方体
圆,扇形,等腰三角形,直角
1
2
3
4
5
6
7
8
9
10
11
12
13
几何体中的顶点、棱、面
4. 如图,几何体圆锥的面数是( B )
A. 1
B. 2
C. 3
D. 4
B
1
2
3
4
5
6
7
8
9
10
11
12
13
5. 如图所示的五棱柱的底面边长都是5 cm,侧棱长12 cm,
它有多少个面?它有多少条棱?它有多少个顶点?它的所
有侧面的面积之和是多少?
【解】它有7个面,15条棱,10个顶点.
它的所有侧面的面积之和为5×12×5=300(cm2).
1
2
3
4
5
6
7
8
9
10
11
12
13
点、线、面、体的关系
6. [2024·杭州下沙期中]汽车的雨刷把玻璃上的雨雪刷干净属
于以下哪项几何知识的实际应用( B )
A. 点动成线 B. 线动成面
C. 面动成体 D. 以上答案都正确
B
1
2
3
4
5
6
7
8
9
10
11
12
13
7. [新趋势·跨学科]在朱自清的《春》中描写春雨“像牛毛,
像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨
看成了线,这说明了 .
点动成线
1
2
3
4
5
6
7
8
9
10
11
12
13
8. 图中图形绕直线l旋转一周后,会得到什么立体图形?用
线连一连.
1
2
3
4
5
6
7
8
9
10
11
12
13
[易错题]对旋转后的几何图形考虑不全面而出错
9. 直角三角形的两条直角边的长分别为8 cm,6 cm,以其中
一条直角边所在直线为轴旋转一周,得到的几何体的底面
积是多少?(结果保留π)
【解】由题意知,以其中一条直角边所在直线为轴旋转一
周所得几何体为圆锥,底面是圆,底面半径是8 cm或6 cm,所以底面积是64π cm2或36π cm2.
1
2
3
4
5
6
7
8
9
10
11
12
13
10. [2024·温州龙湾区模拟]不透明袋子中装有一个几何体模
型,两名同学摸该模型并描述它的特征,甲同学:它有4
个面是三角形;乙同学:它有6条棱.则该模型对应的立
体图形可能是( C )
A. 三棱柱 B. 四棱柱
C. 三棱锥 D. 四棱锥
C
1
2
3
4
5
6
7
8
9
10
11
12
13
11. [立德树人·传统文化]七巧板是我们祖先的一项卓越创
造,被西方人誉为“东方魔板”.如图是一副正方形七巧
板(相同的板规定序号相同).现从七巧板中取出四块(序号
可以相同)拼成一个小正方形(无空隙不重叠),则可以拼
成的序号是( B )
A. ②③③④
B. ①①②③
C. ①①②④
D. ①①②⑤
1
2
3
4
5
6
7
8
9
10
11
12
13
【点拨】
由题意可知,①①②③四块板可拼成一个小正方形
(无空隙不重叠),如图:
故选:B.
B
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图①是三个形状完全相同的几何体(下底面为圆,单
位:厘米),将它们拼成如图②的新几何体,求该新几何
体的体积.(结果保留π)
1
2
3
4
5
6
7
8
9
10
11
12
13
【解】π×(4÷2)2×(4+6)+ [π×(4÷2)2×(4+6)]=40π
+20π=60π(立方厘米).
答:该新几何体的体积为60π立方厘米.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [新视角·规律探究题]简单多面体是各个面都是多边形组
成的几何体,十八世纪瑞士数学家欧拉证明了简单多面
体中顶点数(V)、面数(F)和棱数(E)之间存在一个有趣的
关系式,称为欧拉公式.如表是根据下面的多面体模型列
出的不完整的表:
1
2
3
4
5
6
7
8
9
10
11
12
13
多面体 顶点数 面数 棱数
四面体 4 4 6
长方体 8 6
正八面体 8 12
1
2
3
4
5
6
7
8
9
10
11
12
13
现在有一个多面体,它的每一个面都是三角形,它的面
数(F)和棱数(E)的和为30,则这个多面体的顶点数V
= .
8
1
2
3
4
5
6
7
8
9
10
11
12
13
由表可知这个多面体的顶点数V=2+E-F.
因为有一个多面体,每一个面都是三角形,
所以每相邻两条边重合为一条棱,
所以E= F.
因为E+F=30,所以F=12,所以E=18,
所以V=2+E-F=8.
故答案为8.
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
