6.3 线段的长短比较 课件(共33张PPT)
文档属性
| 名称 | 6.3 线段的长短比较 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 12:19:15 | ||
图片预览









文档简介
(共33张PPT)
6.3 线段的长短比较
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
线段的长短比较
课程目标
掌握比较两条线段长短的两种基本方法:叠合法和度量法。
理解线段中点的概念,能运用中点的性质进行简单计算。
能结合实际情境,运用线段长短比较的方法解决问题,培养动手操作和空间想象能力。
比较线段长短的方法
1. 叠合法
定义:把两条线段的一个端点重合,另一个端点落在同一条直线上,根据另一个端点的位置关系来比较线段的长短。
操作步骤:
设线段\(AB\)和线段\(CD\),将点\(A\)与点\(C\)重合,使线段\(AB\)和线段\(CD\)在同一条直线上,且点\(B\)和点\(D\)在点\(A\)(或点\(C\))的同侧。
结果判断:
如果点\(B\)与点\(D\)重合,那么\(AB = CD\)(如图 1 所示)。
如果点\(B\)在线段\(CD\)上,那么\(AB < CD\)(如图 2 所示)。
如果点\(B\)在线段\(CD\)的延长线上,那么\(AB > CD\)(如图 3 所示)。
实例:比较两根铅笔的长短,可将它们的一端对齐,放在同一直线上,观察另一端的位置来判断。
2. 度量法
定义:用刻度尺分别量出两条线段的长度,再根据长度的大小来比较线段的长短。
操作步骤:
用刻度尺的零刻度线对准线段的一个端点,沿着线段读出另一个端点所对应的刻度值,该刻度值就是线段的长度(单位通常为厘米、毫米等)。
比较两条线段长度的数值大小,数值大的线段较长,数值小的线段较短,数值相等的线段一样长。
实例:用尺子量得线段\(EF\)的长度为\(5\)厘米,线段\(GH\)的长度为\(7\)厘米,因为\(5 < 7\),所以\(EF < GH\)。
两种方法的区别与联系
区别:叠合法是通过直观的重合操作比较,不需要测量工具;度量法是通过测量长度数值比较,需要刻度尺等工具。
联系:两种方法都能准确比较出两条线段的长短,可根据实际情况选择使用。
线段的和与差
已知两条线段\(a\)和\(b\)(\(a > b\)),则:
线段的和:在直线上画线段\(AB = a\),再在线段\(AB\)的延长线上画线段\(BC = b\),则线段\(AC\)就是线段\(a\)与\(b\)的和,记作\(AC = a + b\)。
线段的差:在直线上画线段\(AB = a\),再在线段\(AB\)上画线段\(AD = b\),则线段\(DB\)就是线段\(a\)与\(b\)的差,记作\(DB = a - b\)。
实例:线段\(m = 4\)厘米,线段\(n = 2\)厘米,则\(m + n = 6\)厘米,\(m - n = 2\)厘米。
线段的中点
定义
把一条线段分成两条相等线段的点,叫做这条线段的中点。
如图所示,点\(M\)是线段\(AB\)的中点,则\(AM = MB = \frac{1}{2}AB\),也可以表示为\(AB = 2AM = 2MB\)。
性质应用
例 1:已知线段\(AB = 10\)厘米,点\(C\)是线段\(AB\)的中点,求线段\(AC\)的长度。
解:因为点\(C\)是线段\(AB\)的中点,所以\(AC = \frac{1}{2}AB = \frac{1}{2} 10 = 5\)厘米。
例 2:已知点\(D\)是线段\(EF\)的中点,且\(ED = 3\)厘米,求线段\(EF\)的长度。
解:因为点\(D\)是线段\(EF\)的中点,所以\(EF = 2ED = 2 3 = 6\)厘米。
例 3:线段\(AB = 12\)厘米,点\(C\)在线段\(AB\)上,且\(AC = 4\)厘米,点\(D\)是线段\(BC\)的中点,求线段\(AD\)的长度。
解:因为\(AB = 12\)厘米,\(AC = 4\)厘米,所以\(BC = AB - AC = 12 - 4 = 8\)厘米。
又因为点\(D\)是线段\(BC\)的中点,所以\(CD = \frac{1}{2}BC = \frac{1}{2} 8 = 4\)厘米。
因此,\(AD = AC + CD = 4 + 4 = 8\)厘米。
生活中的应用
道路规划:在修建道路时,比较不同路线的长短,选择较短的路线可以节省材料和时间,这利用了 “两点之间,线段最短” 的性质及线段长短比较的方法。
物品裁剪:裁缝在裁剪布料时,需要比较不同线段的长度,确保布料的尺寸符合要求。
体育比赛:在跳远比赛中,测量运动员跳远距离时,需要比较线段(从起跳线到落地点的垂线段)的长短来决定成绩。
课堂练习
用叠合法比较你手中直尺的长度和一支铅笔的长度。
已知线段\(AB = 8\)厘米,线段\(CD = 6\)厘米,比较\(AB\)和\(CD\)的长短,并计算它们的差。
点\(M\)是线段\(PQ\)的中点,\(PQ = 10\)厘米,求\(PM\)的长度。
线段\(AB = 15\)厘米,点\(C\)在\(AB\)的延长线上,且\(BC = 5\)厘米,点\(D\)是线段\(AC\)的中点,求线段\(BD\)的长度。
总结
比较线段长短的方法有叠合法和度量法,叠合法通过重合端点比较位置,度量法通过测量长度数值比较。
线段中点是将线段分成两条相等线段的点,利用中点性质可进行线段长度的计算,即\(AM = MB = \frac{1}{2}AB\)或\(AB = 2AM = 2MB\)。
线段长短比较在生活中应用广泛,掌握相关方法和概念有助于解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.会用度量法和叠合法比较线段的长短,能说出线段长短比较
的结果。
2.能运用“两点之间线段最短”解释一些实际现象。
3.会用直尺和圆规作一条线段等于已知线段,增强动手能力。
1.度量法(数的比较) 利用刻度尺量出两条线段的长度,
然后比较它们的长短。
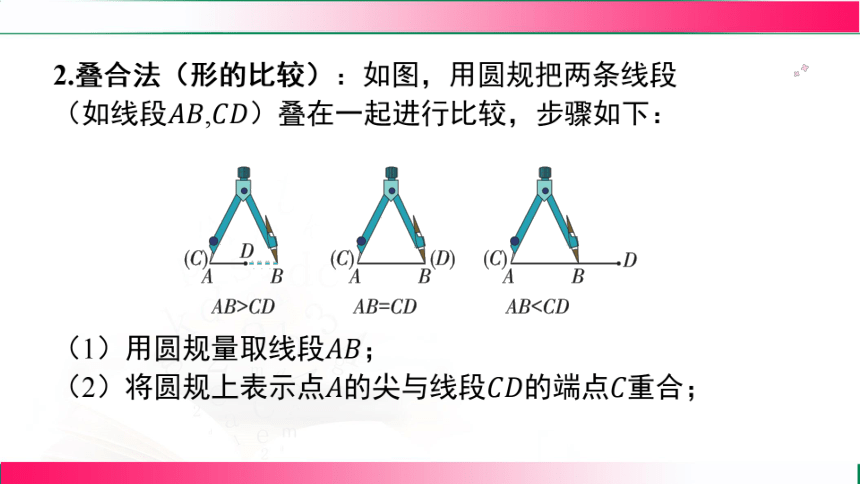
2.叠合法(形的比较) 如图,用圆规把两条线段
(如线段, )叠在一起进行比较,步骤如下:
(1)用圆规量取线段 ;
(2)将圆规上表示点的尖与线段的端点 重合;
(3)若端点落在线段的延长线上,则线段大于
线段 ,可记为 ;
若端点与端点重合,则线段等于线段,可记
为 ;
若端点落在线段上(不含点),则线段小于
线段 ,可记为 。
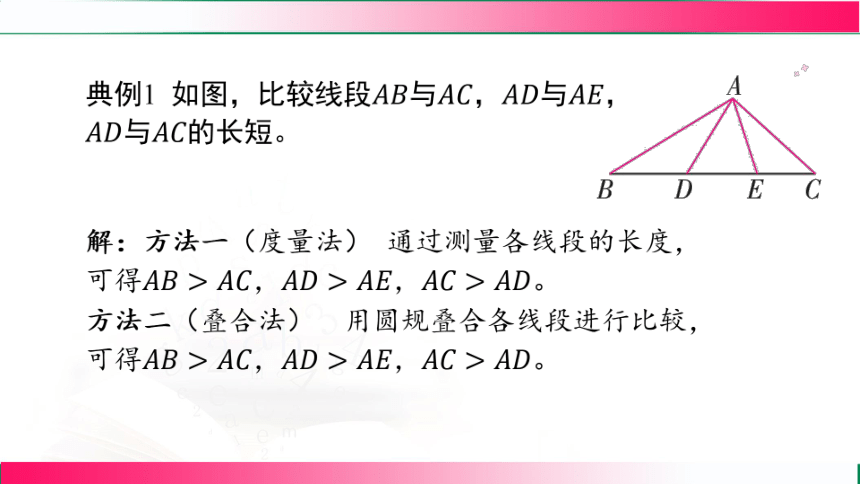
典例1 如图,比较线段与,与 ,
与 的长短。
解:方法一(度量法) 通过测量各线段的长度,
可得 ,, 。
方法二(叠合法) 用圆规叠合各线段进行比较,
可得 ,, 。
1.尺规作图:在数学中,限定用无刻度的直尺和圆规作图,
即是尺规作图。
2.作一条线段等于已知线段 (图1)的方法
作法:如图2,(1)任意画一条射线 ;
(2)用圆规量取已知线段 的长度;
(3)在射线上截取 。
线段 就是所求作的线段。
(作图完毕后,必须写上结论)
图 1
图 2
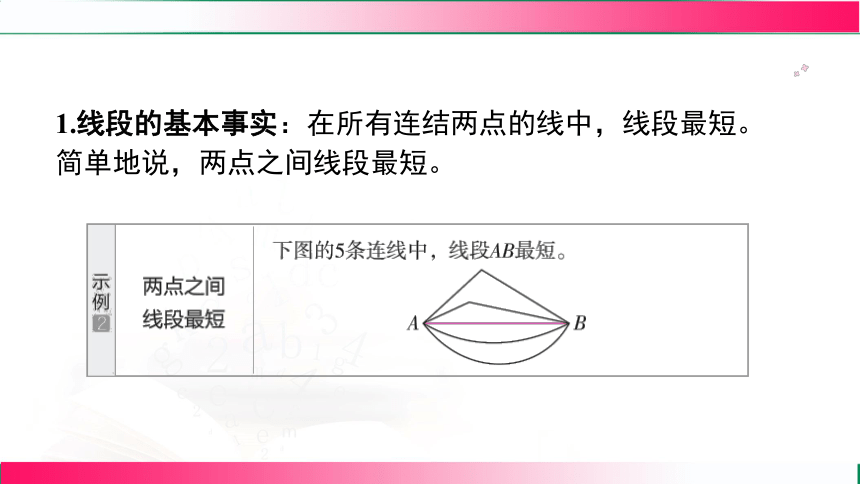
1.线段的基本事实:在所有连结两点的线中,线段最短。
简单地说,两点之间线段最短。
2.两点间的距离:连结两点的线段的长度叫作这两点间的距离。
线段是图形,两点间的距离是线段的长度,两者不同。
典例2 如图所示,在一条
笔直公路的两侧,分别有, 两个村庄,现要在
公路旁建一个汽车站,使汽车站到, 两村的
距离之和最小,问汽车站 的位置应如何确定
解:如图,连结与直线交于点,点 的位置就是
符合条件的汽车站 的位置。
知识过关
①如果两条线段 长度 相等,那么我们就说这两条线段
相等.
②如果两条线段的长度不相等,那么我们就说长度 较大 的
线段大于长度 较小 的线段.
长度
较大
较小
③比较两条线段的长短,可以用刻度尺测量出它们的长度,即
度量法;还可以用圆规把它们“叠”在一起进行比较,即叠
合法.
④在所有连结两点的线中, 线段 最短,简单地说, 两点
之间线段最短 .连结两点的线段的长度叫作 这两点间的
距离 .
线段
两点
之间线段最短
这两点间的
距离
比较线段的长短
1. [2024·绍兴诸暨期末]如图,围绕在正方形四周的四条线
段a,b,c,d中,长度最长的是( D )
A. a B. b C. c D. d
D
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图所示,比较线段a和线段b的长度,结果正确的是
( B )
A. a>b B. a<b
C. a=b D. 无法确定
B
1
2
3
4
5
6
7
8
9
10
11
12
13
3. [2024·金华期末]有不在同一直线上的两条线段AB和
CD,李明很难判断出它们的长短,因此他借助于圆规,
操作如图所示,由此可得出AB CD. (填
“>”“<”或“=”)
>
1
2
3
4
5
6
7
8
9
10
11
12
13
作一条线段等于已知线段
4. [母题 教材P170做一做T3]已知:线段a,如图(1).求作:
线段AB,使AB=a.在下面的作法中,有些地方叙述稍
显笼统,请找出来,并加以改正.
作法:如图(2),①作射线AC;②以点A为一端,作线段
AB=a.AB就是所求作的线段.
1
2
3
4
5
6
7
8
9
10
11
12
13
【解】作法的叙述中第②步太笼统,没交待清楚.这一步
的正确作法为以点A为圆心,以线段a的长为半径画弧,
交射线AC于点B. 线段AB即为所求.或者是用圆规在射
线AC上截取线段AB=a,线段AB即为所求.
1
2
3
4
5
6
7
8
9
10
11
12
13
线段的基本事实
5. 下列四个生活、生产现象:①从A地到B地架设电线,总
是尽可能沿着线段AB架设;②用两个钉子就可以把木条
固定在墙上;③把弯曲的公路改直,就能缩短路程;④植
树时,只要定出两棵树的位置,就能确定同一行树所在的
直线.其中可用“两点之间,线段最短”来解释的现象是
( B )
A. ①② B. ①③
C. ②④ D. ③④
B
1
2
3
4
5
6
7
8
9
10
11
12
13
两点间的距离
6. 如图,A,B两点之间的距离指的是( C )
A. 线段AB
B. 线段AC与线段BC的长度之和
C. 线段AB的长度
D. 线段BC与线段AC的长度之差
C
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 作业本上有A、B两点,圆圆在作直线AB时,发现A点
对应直尺上的刻度示数为3 cm,B点对应直尺上的刻度示
数为8 cm,则A、B两点间的距离为 cm.
5
1
2
3
4
5
6
7
8
9
10
11
12
13
8. [情境题·生活应用]为了解决村庄灌溉问题,政府投资由水
库向A,B,C,D这四个村庄铺设管道,现已知这四个
村庄及水库之间的部分距离(单位:km)如图所示,则把水
库的水输送到这四个村庄铺设管道的总长度最短为
( A )
A. 16 km B. 18 km
C. 18 km D. 20 km
(第8题)
A
1
2
3
4
5
6
7
8
9
10
11
12
13
9. [2024·杭州西湖区期末]如果在数轴上的A,B两点所表示
的有理数分别是x,y,且|x|=3,|y|=1,则
A,B两点间的距离是( C )
A. 4 B. 2
C. 4或2 D. 以上都不对
1
2
3
4
5
6
7
8
9
10
11
12
13
因为|y|=1,所以y=±1,
所以当x与y是同号时,A,B两点间的距离是2;
当x与y是异号时,A,B两点间的距离是4;
所以A,B两点间的距离是2或4.
故选:C.
【点拨】
因为|x|=3,所以x=±3.
C
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图,小红将三角形纸片沿虚线剪去一个角,若剩下四
边形纸片的周长为m,原三角形纸片的周长为n,下列
判断正确的是( A )
A
A. 两点之间,线段最短,故m<n
B. 两点确定一条直线,故m=n
C. 边数越多周长就越大,故m>n
D. 三角形的具体形状以及裁剪的角度都不确
定,故m,n的大小也不确定
(第10题)
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 在图中“ ”内添上字母A,B,C,使AC<AB<
BC.
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图是一幅地图的示意图.
(1)试说出从点A到点F有哪几条路线?(每个点最多经过
一次)
【解】①A-B-E-F;
②A-C-E-F;
③A-D-E-F.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)假设你是一名警察,现正在A处,并得知罪犯已逃离
E处,正向F处这一方向逃跑,那么你将选择哪条路
线去追赶罪犯?请说明你的理由.
【解】选择A-B-E-F路线.
理由:两点之间线段最短.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [新视角·项目探究题]如图,已知四点A,B,C,D.
根据下列语句,画出图形.
(1)顺次连结A,B,C,D,A;
(2)作射线BA,在射线BA上取一点E,使AE=AD;
(3)在四边形ABCD内取一点O,连结OA,OB,OC,
OD,使A,O,C三点不共线,B,O,D三点不
共线;
【解】(1)如图所示.
(2)如图所示.
(3)如图所示.(点O不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
(4)在四边形ABCD内找一点P,使PA+PB+PC+PD
最小.
【解】如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
【拓展应用】为了解决A,B,C,D四个村庄(如图)村民
的饮水问题,政府决定修建一个储水池分别向各村庄供水,
为了节约资金,要求所用的水管最少.不考虑其他因素,请
你确定储水池M的位置.
【拓展应用】如图,连结AC,BD交于点M,则点M即为
所求.
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
6.3 线段的长短比较
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
线段的长短比较
课程目标
掌握比较两条线段长短的两种基本方法:叠合法和度量法。
理解线段中点的概念,能运用中点的性质进行简单计算。
能结合实际情境,运用线段长短比较的方法解决问题,培养动手操作和空间想象能力。
比较线段长短的方法
1. 叠合法
定义:把两条线段的一个端点重合,另一个端点落在同一条直线上,根据另一个端点的位置关系来比较线段的长短。
操作步骤:
设线段\(AB\)和线段\(CD\),将点\(A\)与点\(C\)重合,使线段\(AB\)和线段\(CD\)在同一条直线上,且点\(B\)和点\(D\)在点\(A\)(或点\(C\))的同侧。
结果判断:
如果点\(B\)与点\(D\)重合,那么\(AB = CD\)(如图 1 所示)。
如果点\(B\)在线段\(CD\)上,那么\(AB < CD\)(如图 2 所示)。
如果点\(B\)在线段\(CD\)的延长线上,那么\(AB > CD\)(如图 3 所示)。
实例:比较两根铅笔的长短,可将它们的一端对齐,放在同一直线上,观察另一端的位置来判断。
2. 度量法
定义:用刻度尺分别量出两条线段的长度,再根据长度的大小来比较线段的长短。
操作步骤:
用刻度尺的零刻度线对准线段的一个端点,沿着线段读出另一个端点所对应的刻度值,该刻度值就是线段的长度(单位通常为厘米、毫米等)。
比较两条线段长度的数值大小,数值大的线段较长,数值小的线段较短,数值相等的线段一样长。
实例:用尺子量得线段\(EF\)的长度为\(5\)厘米,线段\(GH\)的长度为\(7\)厘米,因为\(5 < 7\),所以\(EF < GH\)。
两种方法的区别与联系
区别:叠合法是通过直观的重合操作比较,不需要测量工具;度量法是通过测量长度数值比较,需要刻度尺等工具。
联系:两种方法都能准确比较出两条线段的长短,可根据实际情况选择使用。
线段的和与差
已知两条线段\(a\)和\(b\)(\(a > b\)),则:
线段的和:在直线上画线段\(AB = a\),再在线段\(AB\)的延长线上画线段\(BC = b\),则线段\(AC\)就是线段\(a\)与\(b\)的和,记作\(AC = a + b\)。
线段的差:在直线上画线段\(AB = a\),再在线段\(AB\)上画线段\(AD = b\),则线段\(DB\)就是线段\(a\)与\(b\)的差,记作\(DB = a - b\)。
实例:线段\(m = 4\)厘米,线段\(n = 2\)厘米,则\(m + n = 6\)厘米,\(m - n = 2\)厘米。
线段的中点
定义
把一条线段分成两条相等线段的点,叫做这条线段的中点。
如图所示,点\(M\)是线段\(AB\)的中点,则\(AM = MB = \frac{1}{2}AB\),也可以表示为\(AB = 2AM = 2MB\)。
性质应用
例 1:已知线段\(AB = 10\)厘米,点\(C\)是线段\(AB\)的中点,求线段\(AC\)的长度。
解:因为点\(C\)是线段\(AB\)的中点,所以\(AC = \frac{1}{2}AB = \frac{1}{2} 10 = 5\)厘米。
例 2:已知点\(D\)是线段\(EF\)的中点,且\(ED = 3\)厘米,求线段\(EF\)的长度。
解:因为点\(D\)是线段\(EF\)的中点,所以\(EF = 2ED = 2 3 = 6\)厘米。
例 3:线段\(AB = 12\)厘米,点\(C\)在线段\(AB\)上,且\(AC = 4\)厘米,点\(D\)是线段\(BC\)的中点,求线段\(AD\)的长度。
解:因为\(AB = 12\)厘米,\(AC = 4\)厘米,所以\(BC = AB - AC = 12 - 4 = 8\)厘米。
又因为点\(D\)是线段\(BC\)的中点,所以\(CD = \frac{1}{2}BC = \frac{1}{2} 8 = 4\)厘米。
因此,\(AD = AC + CD = 4 + 4 = 8\)厘米。
生活中的应用
道路规划:在修建道路时,比较不同路线的长短,选择较短的路线可以节省材料和时间,这利用了 “两点之间,线段最短” 的性质及线段长短比较的方法。
物品裁剪:裁缝在裁剪布料时,需要比较不同线段的长度,确保布料的尺寸符合要求。
体育比赛:在跳远比赛中,测量运动员跳远距离时,需要比较线段(从起跳线到落地点的垂线段)的长短来决定成绩。
课堂练习
用叠合法比较你手中直尺的长度和一支铅笔的长度。
已知线段\(AB = 8\)厘米,线段\(CD = 6\)厘米,比较\(AB\)和\(CD\)的长短,并计算它们的差。
点\(M\)是线段\(PQ\)的中点,\(PQ = 10\)厘米,求\(PM\)的长度。
线段\(AB = 15\)厘米,点\(C\)在\(AB\)的延长线上,且\(BC = 5\)厘米,点\(D\)是线段\(AC\)的中点,求线段\(BD\)的长度。
总结
比较线段长短的方法有叠合法和度量法,叠合法通过重合端点比较位置,度量法通过测量长度数值比较。
线段中点是将线段分成两条相等线段的点,利用中点性质可进行线段长度的计算,即\(AM = MB = \frac{1}{2}AB\)或\(AB = 2AM = 2MB\)。
线段长短比较在生活中应用广泛,掌握相关方法和概念有助于解决实际问题。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.会用度量法和叠合法比较线段的长短,能说出线段长短比较
的结果。
2.能运用“两点之间线段最短”解释一些实际现象。
3.会用直尺和圆规作一条线段等于已知线段,增强动手能力。
1.度量法(数的比较) 利用刻度尺量出两条线段的长度,
然后比较它们的长短。
2.叠合法(形的比较) 如图,用圆规把两条线段
(如线段, )叠在一起进行比较,步骤如下:
(1)用圆规量取线段 ;
(2)将圆规上表示点的尖与线段的端点 重合;
(3)若端点落在线段的延长线上,则线段大于
线段 ,可记为 ;
若端点与端点重合,则线段等于线段,可记
为 ;
若端点落在线段上(不含点),则线段小于
线段 ,可记为 。
典例1 如图,比较线段与,与 ,
与 的长短。
解:方法一(度量法) 通过测量各线段的长度,
可得 ,, 。
方法二(叠合法) 用圆规叠合各线段进行比较,
可得 ,, 。
1.尺规作图:在数学中,限定用无刻度的直尺和圆规作图,
即是尺规作图。
2.作一条线段等于已知线段 (图1)的方法
作法:如图2,(1)任意画一条射线 ;
(2)用圆规量取已知线段 的长度;
(3)在射线上截取 。
线段 就是所求作的线段。
(作图完毕后,必须写上结论)
图 1
图 2
1.线段的基本事实:在所有连结两点的线中,线段最短。
简单地说,两点之间线段最短。
2.两点间的距离:连结两点的线段的长度叫作这两点间的距离。
线段是图形,两点间的距离是线段的长度,两者不同。
典例2 如图所示,在一条
笔直公路的两侧,分别有, 两个村庄,现要在
公路旁建一个汽车站,使汽车站到, 两村的
距离之和最小,问汽车站 的位置应如何确定
解:如图,连结与直线交于点,点 的位置就是
符合条件的汽车站 的位置。
知识过关
①如果两条线段 长度 相等,那么我们就说这两条线段
相等.
②如果两条线段的长度不相等,那么我们就说长度 较大 的
线段大于长度 较小 的线段.
长度
较大
较小
③比较两条线段的长短,可以用刻度尺测量出它们的长度,即
度量法;还可以用圆规把它们“叠”在一起进行比较,即叠
合法.
④在所有连结两点的线中, 线段 最短,简单地说, 两点
之间线段最短 .连结两点的线段的长度叫作 这两点间的
距离 .
线段
两点
之间线段最短
这两点间的
距离
比较线段的长短
1. [2024·绍兴诸暨期末]如图,围绕在正方形四周的四条线
段a,b,c,d中,长度最长的是( D )
A. a B. b C. c D. d
D
1
2
3
4
5
6
7
8
9
10
11
12
13
2. 如图所示,比较线段a和线段b的长度,结果正确的是
( B )
A. a>b B. a<b
C. a=b D. 无法确定
B
1
2
3
4
5
6
7
8
9
10
11
12
13
3. [2024·金华期末]有不在同一直线上的两条线段AB和
CD,李明很难判断出它们的长短,因此他借助于圆规,
操作如图所示,由此可得出AB CD. (填
“>”“<”或“=”)
>
1
2
3
4
5
6
7
8
9
10
11
12
13
作一条线段等于已知线段
4. [母题 教材P170做一做T3]已知:线段a,如图(1).求作:
线段AB,使AB=a.在下面的作法中,有些地方叙述稍
显笼统,请找出来,并加以改正.
作法:如图(2),①作射线AC;②以点A为一端,作线段
AB=a.AB就是所求作的线段.
1
2
3
4
5
6
7
8
9
10
11
12
13
【解】作法的叙述中第②步太笼统,没交待清楚.这一步
的正确作法为以点A为圆心,以线段a的长为半径画弧,
交射线AC于点B. 线段AB即为所求.或者是用圆规在射
线AC上截取线段AB=a,线段AB即为所求.
1
2
3
4
5
6
7
8
9
10
11
12
13
线段的基本事实
5. 下列四个生活、生产现象:①从A地到B地架设电线,总
是尽可能沿着线段AB架设;②用两个钉子就可以把木条
固定在墙上;③把弯曲的公路改直,就能缩短路程;④植
树时,只要定出两棵树的位置,就能确定同一行树所在的
直线.其中可用“两点之间,线段最短”来解释的现象是
( B )
A. ①② B. ①③
C. ②④ D. ③④
B
1
2
3
4
5
6
7
8
9
10
11
12
13
两点间的距离
6. 如图,A,B两点之间的距离指的是( C )
A. 线段AB
B. 线段AC与线段BC的长度之和
C. 线段AB的长度
D. 线段BC与线段AC的长度之差
C
1
2
3
4
5
6
7
8
9
10
11
12
13
7. 作业本上有A、B两点,圆圆在作直线AB时,发现A点
对应直尺上的刻度示数为3 cm,B点对应直尺上的刻度示
数为8 cm,则A、B两点间的距离为 cm.
5
1
2
3
4
5
6
7
8
9
10
11
12
13
8. [情境题·生活应用]为了解决村庄灌溉问题,政府投资由水
库向A,B,C,D这四个村庄铺设管道,现已知这四个
村庄及水库之间的部分距离(单位:km)如图所示,则把水
库的水输送到这四个村庄铺设管道的总长度最短为
( A )
A. 16 km B. 18 km
C. 18 km D. 20 km
(第8题)
A
1
2
3
4
5
6
7
8
9
10
11
12
13
9. [2024·杭州西湖区期末]如果在数轴上的A,B两点所表示
的有理数分别是x,y,且|x|=3,|y|=1,则
A,B两点间的距离是( C )
A. 4 B. 2
C. 4或2 D. 以上都不对
1
2
3
4
5
6
7
8
9
10
11
12
13
因为|y|=1,所以y=±1,
所以当x与y是同号时,A,B两点间的距离是2;
当x与y是异号时,A,B两点间的距离是4;
所以A,B两点间的距离是2或4.
故选:C.
【点拨】
因为|x|=3,所以x=±3.
C
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
10. 如图,小红将三角形纸片沿虚线剪去一个角,若剩下四
边形纸片的周长为m,原三角形纸片的周长为n,下列
判断正确的是( A )
A
A. 两点之间,线段最短,故m<n
B. 两点确定一条直线,故m=n
C. 边数越多周长就越大,故m>n
D. 三角形的具体形状以及裁剪的角度都不确
定,故m,n的大小也不确定
(第10题)
1
2
3
4
5
6
7
8
9
10
11
12
13
11. 在图中“ ”内添上字母A,B,C,使AC<AB<
BC.
A
B
C
1
2
3
4
5
6
7
8
9
10
11
12
13
12. 如图是一幅地图的示意图.
(1)试说出从点A到点F有哪几条路线?(每个点最多经过
一次)
【解】①A-B-E-F;
②A-C-E-F;
③A-D-E-F.
1
2
3
4
5
6
7
8
9
10
11
12
13
(2)假设你是一名警察,现正在A处,并得知罪犯已逃离
E处,正向F处这一方向逃跑,那么你将选择哪条路
线去追赶罪犯?请说明你的理由.
【解】选择A-B-E-F路线.
理由:两点之间线段最短.
1
2
3
4
5
6
7
8
9
10
11
12
13
13. [新视角·项目探究题]如图,已知四点A,B,C,D.
根据下列语句,画出图形.
(1)顺次连结A,B,C,D,A;
(2)作射线BA,在射线BA上取一点E,使AE=AD;
(3)在四边形ABCD内取一点O,连结OA,OB,OC,
OD,使A,O,C三点不共线,B,O,D三点不
共线;
【解】(1)如图所示.
(2)如图所示.
(3)如图所示.(点O不唯一)
1
2
3
4
5
6
7
8
9
10
11
12
13
(4)在四边形ABCD内找一点P,使PA+PB+PC+PD
最小.
【解】如图所示.
1
2
3
4
5
6
7
8
9
10
11
12
13
【拓展应用】为了解决A,B,C,D四个村庄(如图)村民
的饮水问题,政府决定修建一个储水池分别向各村庄供水,
为了节约资金,要求所用的水管最少.不考虑其他因素,请
你确定储水池M的位置.
【拓展应用】如图,连结AC,BD交于点M,则点M即为
所求.
1
2
3
4
5
6
7
8
9
10
11
12
13
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
