6.5 角与角的度量 课件(共39张PPT)
文档属性
| 名称 | 6.5 角与角的度量 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 12:24:17 | ||
图片预览











文档简介
(共39张PPT)
6.5 角与角的度量
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
角与角的度量
课程目标
理解角的概念,能准确描述角的形成过程。
掌握角的表示方法,能根据不同情况正确表示角。
了解角的度量单位(度、分、秒)及它们之间的换算关系。
学会使用量角器度量角的大小,能准确读出角的度数。
知道角按大小的分类,能区分不同类型的角。
角的概念
定义
由两条具有公共端点的射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。
角也可以看作是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。射线旋转时经过的平面部分是角的内部,未经过的部分是角的外部。
实例:钟表上时针和分针组成的图形是角;三角板的每个拐角都是角。
角的表示方法
角的表示方法有多种,具体如下:
用三个大写字母表示:用角的顶点字母和两边上各取一个点的字母表示,顶点字母必须写在中间,如\(\angle AOB\)(\(O\)为顶点,\(A\)、\(B\)分别为两边上的点)。
用一个大写字母表示:当以某一点为顶点的角只有一个时,可以用顶点字母表示,如\(\angle O\)(顶点为\(O\),且只有一个角)。
用一个数字表示:在角的内部靠近顶点处画上弧线,标上数字,如\(\angle 1\)、\(\angle 2\)。
用一个小写希腊字母表示:在角的内部靠近顶点处画上弧线,标上小写希腊字母(如\(\alpha\)、\(\beta\)、\(\gamma\)等),如\(\angle \alpha\)、\(\angle \beta\)。
注意:用一个大写字母表示角时,必须保证顶点处只有一个角,否则容易混淆。例如,顶点\(O\)处有多个角时,不能用\(\angle O\)表示其中某一个角。
角的度量单位及换算
度量单位
角的度量单位是度、分、秒,分别用符号 “\( °\)”“\( \)”“\( \)” 表示。
把一个周角平均分成 360 等份,每一份就是 1 度的角,记作\(1 °\)。
把 1 度的角平均分成 60 等份,每一份就是 1 分的角,记作\(1 \)。
把 1 分的角平均分成 60 等份,每一份就是 1 秒的角,记作\(1 \)。
换算关系
\(1 °=60 \)
\(1 =60 \)
\(1 °=3600 \)
换算示例
例 1:将\(3.5 °\)换算成度和分。
解:因为\(1 °=60 \),所以\(0.5 °=0.5 60 =30 \),因此\(3.5 °=3 °30 \)。
例 2:将\(4 °20 \)换算成度。
解:因为\(1 =(\frac{1}{60}) °\),所以\(20 =20 (\frac{1}{60}) ° 0.33 °\),因此\(4 °20 4.33 °\)。
例 3:将\(120 \)换算成度。
解:因为\(1 °=60 \),所以\(120 =120 ·60=2 °\)。
例 4:将\(3600 \)换算成度。
解:因为\(1 °=3600 \),所以\(3600 =1 °\)。
角的度量方法
使用量角器度量角的步骤:
点点重合:把量角器的中心与角的顶点重合。
线边重合:把量角器的 0 刻度线与角的一条边重合。
读刻度:角的另一条边所对的量角器上的刻度,就是这个角的度数。
注意:
量角器有内外圈刻度,当角的一条边与内圈 0 刻度线重合时,读内圈刻度;与外圈 0 刻度线重合时,读外圈刻度。
读数时要注意区分刻度的大小,避免读错。
示例:度量\(\angle AOB\)的度数,将量角器中心与\(O\)重合,一条边\(OA\)与内圈 0 刻度线重合,另一条边\(OB\)对内圈刻度\(60 °\),则\(\angle AOB = 60 °\)。
角的分类(按大小)
根据角的度数大小,角可以分为以下几类:
锐角:大于\(0 °\)且小于\(90 °\)的角,如\(30 °\)、\(60 °\)的角。
直角:等于\(90 °\)的角,通常用 “\(\text{ }\)” 表示直角符号,如\(\angle A = 90 °\),则\(\angle A\)是直角。
钝角:大于\(90 °\)且小于\(180 °\)的角,如\(120 °\)、\(150 °\)的角。
平角:等于\(180 °\)的角,平角的两边成一条直线,如一条射线绕端点旋转\(180 °\)形成的角是平角。
周角:等于\(360 °\)的角,周角的两边重合,如一条射线绕端点旋转\(360 °\)形成的角是周角。
关系:\(1\)周角\(=2\)平角\(=4\)直角\(=360 °\);\(1\)平角\(=2\)直角\(=180 °\)。
生活中的角
角在生活中随处可见:
门窗的拐角通常是直角;
打开的扇子形成的角可以是锐角、钝角;
钟表上,3 时整时针和分针成直角,6 时整成平角,12 时整成周角。
课堂练习
说出下列角的表示方法是否正确,若不正确,请改正:
以\(O\)为顶点,\(OA\)、\(OB\)为边的角表示为\(\angle O\)(顶点\(O\)处只有这一个角)。
图中\(\angle 1\)可以表示为\(\angle AOB\)。
进行单位换算:
\(2.25 °=(\quad) °(\quad) \)
\(3 °45 =(\quad) °\)
\(1800 =(\quad) °\)
用量角器度量你手中三角板的各个角的度数,并判断它们是什么角。
一个角是平角的一半,这个角是多少度?是什么角?
总结
角是由公共端点的两条射线组成的图形,也可看作射线绕端点旋转形成的图形,有多种表示方法。
角的度量单位是度、分、秒,换算关系为\(1 °=60 \),\(1 =60 \),\(1 °=3600 \)。
用量角器度量角时要做到 “点点重合”“线边重合”,再读刻度。
角按大小分为锐角、直角、钝角、平角、周角,它们之间存在特定的数量关系。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解角的有关概念,会表示角,发展抽象能力。
2.通过角的定义,理解平角、周角的定义。
3.认识度、分、秒,并能进行简单的换算,提高运算能力。
1.角的“静态”定义
定义 图示 解读
“静止” 的观点 由两条有公共 端点的射线所 组成的图形。 _________________________________ 这个公共端点叫作这
个角的顶点,这两条
射线是角的两条边。
2.角的几何符号为“ ”,读作“角”,角的一般表示方法有
以下四种:
表示方法 图示 记法 说明
用三个大写 字母表示 _____________________________
表示方法 图示 记法 说明
用一个数字 表示 _______________________ 在靠近角的顶点处加上弧
线,并标上数字或希腊字
母。该表示方法形象、直
观。
用一个希腊 字母表示 用角的顶点 字母表示 ___________________________ 当角的顶点处只有一个角
时,可用这个顶点字母来表
示。
典例1 仔细观察右图,将符合要求的角写在横线
上(只写小于平角的角)。
(1)能用一个大写字母表示的角:_________;
,
(2)必须用三个大写字母表示的角:_____________
_______________________;
,,,,
(3)以 为顶点的角:_____________________。
,,
解析:
问题序号 条件 图中符合条件的角
(1) 顶点处只有一个角。
(2) 顶点处有多个角。
(3)
1.角的“动态”定义
定义 图示 解读
“运动” 的观点 由一条射线 绕着它的端 点旋转而成 的图形。 _____________________________________________ 起始位置的射线叫
作角的始边,终止
位置的射线叫作角
的终边。
我们平时画角时,只画角的一部分,角的两边是两条射线。
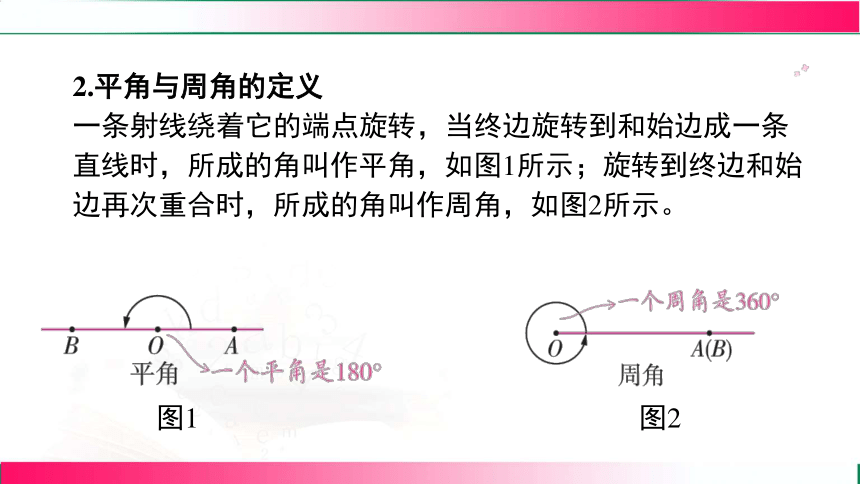
2.平角与周角的定义
一条射线绕着它的端点旋转,当终边旋转到和始边成一条
直线时,所成的角叫作平角,如图1所示;旋转到终边和始
边再次重合时,所成的角叫作周角,如图2所示。
图1
图2
(1)平角的两边成一条直线,但不能说直线
就是平角或平角就是直线。(2)周角的两边重合形成
一条射线,但不能说周角就是射线或射线就是周角。
典例2 给出下列几种说法:
①两条射线组成的图形是角;
②角的边越长,角越大;
③角的两边是两条射线;
④因为平角的两边成一条直线,所以一条直线可以看成一个平角;
⑤周角是一条射线。其中,正确的有( )
A
A.1个 B.2个 C.3个 D.4个
解析:
序号 是否正确 理由
① 若两条射线没有公共端点,则构成的图形不是
角。
② 角的大小只与构成角两边的射线张开的幅度有
关,与角两边的长短无关。
序号 是否正确 理由
③ √ 角的两边是两条具有公共端点的射线。
④ 平角是由顶点和两条边组成的图形,平角和直
线是两个不同的概念。
⑤ 周角的两条边重合成一条射线,周角和射线是
两个不同的概念。
1.角的度量单位:度、分、秒是角的基本度量单位。把周角等
分为360份,每一份就是 的角;把 的角等分成60份,每一
份就是1分,记作;把1分的角等分成60份,每一份就是1秒,
记作 。
2.角的单位换算:
, ;, ;
, ;1周角 ,1平角 。
它们之间的换算是60进制,这与时间的时、分、秒
之间的换算是一样的。
典例3 (1)把 转化为用度、分、秒表示的形式;
解: ;
(2)把 转化成用度表示的形式。
解: 。
知识过关
①角是由两条有公共 端点 的 射线 所组成的图形.这个
公共 端点 叫作这个角的 顶点 .角也可以看成是由一
条 射线 绕着它的 端点 旋转而成的图形.起始位置的
射线叫作角的 始边 ,终止位置的射线叫作角的 终边 .
②一个周角等于 360° ,一个平角等于 180° .
③1°= 60 ',1'= 60 ″;1″= ',1'= °.
端点
射线
端点
顶点
射线
端点
始边
终
边
360°
180°
60
60
角的概念及表示
1. 给出下列说法:①两条射线所组成的图形叫作角;②一条
射线旋转而成的图形叫作角;③两条具有公共端点的射线
组成的图形叫作角;④角是一条射线绕它的端点旋转形成
的图形.其中,正确的有( B )
A. 1个 B. 2个
C. 3个 D. 4个
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. 如图,能用∠1、∠EOF、∠O三种方法表示同一个角的
图形是( D )
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3. 下列关于平角和周角的说法正确的是( D )
A. 平角是一条线段
B. 周角是一条射线
C. 周角只有一条边
D. 反向延长射线OA,就形成一个平角
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. [母题 教材P179课内练习T1]如图,图中共有几个角?用
适当的方式表示这些角.
【解】图中共有6个角,分别是:∠1,∠DOB,
∠DOA,∠2,∠COA,∠3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
角的度量
5. 如图所示,用量角器度量∠AOB,可以读出∠AOB的度
数为( B )
A. 45°
B. 55°
C. 125°
D. 135°
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
角的计算
6. [2024·金华期末]将20°30'转化为度的形式,即:20°30'
= °.
7. [2024·宁波月考]35.7°= ° '.
20.5
35
42
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)48°39'+67°31';
【解】48°39'+67°31'
=115°70'
=116°10';
8. 计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)23°53'×2-17°43'.
【解】23°53'×2-17°43'
=46°106'-17°43'
=29°63'
=30°3'.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
钟面角
9. [母题·教材P180作业题T1 2024·广西]如图,2时整,钟表
的时针和分针所成的锐角为( C )
A. 20°
B. 40°
C. 60°
D. 80°
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. 钟表上从早上6点30分到早上8点10分,时针所走的度数
为( B )
A. 45° B. 50°
C. 55° D. 60°
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. 图中角的表示方法正确的个数有( B )
A. 1个 B. 2个
C. 3个 D. 4个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
第一个图形应为∠CAB,表示不正确;第二个图形
∠AOB是平角,表示正确;第三个图形,直线与平角是
两个概念,平角有顶点,直线没有,表示不正确;第四
个图形,表示为∠CAB,正确.综上所述,表示正确的
有2个,故选B.
【答案】
B
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 已知∠α=30°18',∠β=30.18°,∠γ=30.3°,则
( B )
A. ∠α=∠β B. ∠α=∠γ
C. ∠β=∠γ D. 无法比较大小
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13. [2024·安庆期末]某同学晚上6点多开始做作业,他家墙上
时钟的时针和分针的夹角是120°,他做完作业后还是6
点多,且时针和分针的夹角还是120°,此同学做作业大
约用了 分钟.
44
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设开始做作业时的时间是6点x分,
6x-0.5x=180-120,解得x≈11;
设做完作业后的时间是6点y分,
6y-0.5y=180+120,解得y≈55,
所以此同学做作业大约用了55-11=44(分钟).
【点拨】
分针速度是时针速度的12倍,分针一分钟走6°,对
应时针走0.5°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. 计算:
(1)11°23'26″×3;(结果用度、分、秒表示)
【解】11°23'26″×3=33°69'78″=34°10'18″;
(2)40°40'÷3;(结果用度、分、秒表示)
【解】40°40'÷3=39°99'60″÷3=13°33'20″;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)90°-79°18'6″;(结果用度、分、秒表示)
【解】90°-79°18'6″=89°59'60″-79°18'6″=
10°41'54″;
(4)24°13'37″+35°46'23″.(结果用度表示)
【解】24°13'37″+35°46'23″=59°59'60″=60°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. [新视角·规律探究题] 如图,观察图,回答下列问题:
(1)图①中有几个角?
【解】图①中有1个角;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)图②中有几个角?
【解】图②中有3个角;
(3)图③中有几个角?
【解】图③中有6个角;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(4)以此类推,如图④所示,若一个角内有n条射线,此
时共有多少个角?
【解】由前三问类推,角内有n条射线时,图中共有
(n+2)条射线,则角的个数为 .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看!
6.5 角与角的度量
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
角与角的度量
课程目标
理解角的概念,能准确描述角的形成过程。
掌握角的表示方法,能根据不同情况正确表示角。
了解角的度量单位(度、分、秒)及它们之间的换算关系。
学会使用量角器度量角的大小,能准确读出角的度数。
知道角按大小的分类,能区分不同类型的角。
角的概念
定义
由两条具有公共端点的射线组成的图形叫做角,这个公共端点叫做角的顶点,这两条射线叫做角的边。
角也可以看作是一条射线绕着它的端点从一个位置旋转到另一个位置所形成的图形。射线旋转时经过的平面部分是角的内部,未经过的部分是角的外部。
实例:钟表上时针和分针组成的图形是角;三角板的每个拐角都是角。
角的表示方法
角的表示方法有多种,具体如下:
用三个大写字母表示:用角的顶点字母和两边上各取一个点的字母表示,顶点字母必须写在中间,如\(\angle AOB\)(\(O\)为顶点,\(A\)、\(B\)分别为两边上的点)。
用一个大写字母表示:当以某一点为顶点的角只有一个时,可以用顶点字母表示,如\(\angle O\)(顶点为\(O\),且只有一个角)。
用一个数字表示:在角的内部靠近顶点处画上弧线,标上数字,如\(\angle 1\)、\(\angle 2\)。
用一个小写希腊字母表示:在角的内部靠近顶点处画上弧线,标上小写希腊字母(如\(\alpha\)、\(\beta\)、\(\gamma\)等),如\(\angle \alpha\)、\(\angle \beta\)。
注意:用一个大写字母表示角时,必须保证顶点处只有一个角,否则容易混淆。例如,顶点\(O\)处有多个角时,不能用\(\angle O\)表示其中某一个角。
角的度量单位及换算
度量单位
角的度量单位是度、分、秒,分别用符号 “\( °\)”“\( \)”“\( \)” 表示。
把一个周角平均分成 360 等份,每一份就是 1 度的角,记作\(1 °\)。
把 1 度的角平均分成 60 等份,每一份就是 1 分的角,记作\(1 \)。
把 1 分的角平均分成 60 等份,每一份就是 1 秒的角,记作\(1 \)。
换算关系
\(1 °=60 \)
\(1 =60 \)
\(1 °=3600 \)
换算示例
例 1:将\(3.5 °\)换算成度和分。
解:因为\(1 °=60 \),所以\(0.5 °=0.5 60 =30 \),因此\(3.5 °=3 °30 \)。
例 2:将\(4 °20 \)换算成度。
解:因为\(1 =(\frac{1}{60}) °\),所以\(20 =20 (\frac{1}{60}) ° 0.33 °\),因此\(4 °20 4.33 °\)。
例 3:将\(120 \)换算成度。
解:因为\(1 °=60 \),所以\(120 =120 ·60=2 °\)。
例 4:将\(3600 \)换算成度。
解:因为\(1 °=3600 \),所以\(3600 =1 °\)。
角的度量方法
使用量角器度量角的步骤:
点点重合:把量角器的中心与角的顶点重合。
线边重合:把量角器的 0 刻度线与角的一条边重合。
读刻度:角的另一条边所对的量角器上的刻度,就是这个角的度数。
注意:
量角器有内外圈刻度,当角的一条边与内圈 0 刻度线重合时,读内圈刻度;与外圈 0 刻度线重合时,读外圈刻度。
读数时要注意区分刻度的大小,避免读错。
示例:度量\(\angle AOB\)的度数,将量角器中心与\(O\)重合,一条边\(OA\)与内圈 0 刻度线重合,另一条边\(OB\)对内圈刻度\(60 °\),则\(\angle AOB = 60 °\)。
角的分类(按大小)
根据角的度数大小,角可以分为以下几类:
锐角:大于\(0 °\)且小于\(90 °\)的角,如\(30 °\)、\(60 °\)的角。
直角:等于\(90 °\)的角,通常用 “\(\text{ }\)” 表示直角符号,如\(\angle A = 90 °\),则\(\angle A\)是直角。
钝角:大于\(90 °\)且小于\(180 °\)的角,如\(120 °\)、\(150 °\)的角。
平角:等于\(180 °\)的角,平角的两边成一条直线,如一条射线绕端点旋转\(180 °\)形成的角是平角。
周角:等于\(360 °\)的角,周角的两边重合,如一条射线绕端点旋转\(360 °\)形成的角是周角。
关系:\(1\)周角\(=2\)平角\(=4\)直角\(=360 °\);\(1\)平角\(=2\)直角\(=180 °\)。
生活中的角
角在生活中随处可见:
门窗的拐角通常是直角;
打开的扇子形成的角可以是锐角、钝角;
钟表上,3 时整时针和分针成直角,6 时整成平角,12 时整成周角。
课堂练习
说出下列角的表示方法是否正确,若不正确,请改正:
以\(O\)为顶点,\(OA\)、\(OB\)为边的角表示为\(\angle O\)(顶点\(O\)处只有这一个角)。
图中\(\angle 1\)可以表示为\(\angle AOB\)。
进行单位换算:
\(2.25 °=(\quad) °(\quad) \)
\(3 °45 =(\quad) °\)
\(1800 =(\quad) °\)
用量角器度量你手中三角板的各个角的度数,并判断它们是什么角。
一个角是平角的一半,这个角是多少度?是什么角?
总结
角是由公共端点的两条射线组成的图形,也可看作射线绕端点旋转形成的图形,有多种表示方法。
角的度量单位是度、分、秒,换算关系为\(1 °=60 \),\(1 =60 \),\(1 °=3600 \)。
用量角器度量角时要做到 “点点重合”“线边重合”,再读刻度。
角按大小分为锐角、直角、钝角、平角、周角,它们之间存在特定的数量关系。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.理解角的有关概念,会表示角,发展抽象能力。
2.通过角的定义,理解平角、周角的定义。
3.认识度、分、秒,并能进行简单的换算,提高运算能力。
1.角的“静态”定义
定义 图示 解读
“静止” 的观点 由两条有公共 端点的射线所 组成的图形。 _________________________________ 这个公共端点叫作这
个角的顶点,这两条
射线是角的两条边。
2.角的几何符号为“ ”,读作“角”,角的一般表示方法有
以下四种:
表示方法 图示 记法 说明
用三个大写 字母表示 _____________________________
表示方法 图示 记法 说明
用一个数字 表示 _______________________ 在靠近角的顶点处加上弧
线,并标上数字或希腊字
母。该表示方法形象、直
观。
用一个希腊 字母表示 用角的顶点 字母表示 ___________________________ 当角的顶点处只有一个角
时,可用这个顶点字母来表
示。
典例1 仔细观察右图,将符合要求的角写在横线
上(只写小于平角的角)。
(1)能用一个大写字母表示的角:_________;
,
(2)必须用三个大写字母表示的角:_____________
_______________________;
,,,,
(3)以 为顶点的角:_____________________。
,,
解析:
问题序号 条件 图中符合条件的角
(1) 顶点处只有一个角。
(2) 顶点处有多个角。
(3)
1.角的“动态”定义
定义 图示 解读
“运动” 的观点 由一条射线 绕着它的端 点旋转而成 的图形。 _____________________________________________ 起始位置的射线叫
作角的始边,终止
位置的射线叫作角
的终边。
我们平时画角时,只画角的一部分,角的两边是两条射线。
2.平角与周角的定义
一条射线绕着它的端点旋转,当终边旋转到和始边成一条
直线时,所成的角叫作平角,如图1所示;旋转到终边和始
边再次重合时,所成的角叫作周角,如图2所示。
图1
图2
(1)平角的两边成一条直线,但不能说直线
就是平角或平角就是直线。(2)周角的两边重合形成
一条射线,但不能说周角就是射线或射线就是周角。
典例2 给出下列几种说法:
①两条射线组成的图形是角;
②角的边越长,角越大;
③角的两边是两条射线;
④因为平角的两边成一条直线,所以一条直线可以看成一个平角;
⑤周角是一条射线。其中,正确的有( )
A
A.1个 B.2个 C.3个 D.4个
解析:
序号 是否正确 理由
① 若两条射线没有公共端点,则构成的图形不是
角。
② 角的大小只与构成角两边的射线张开的幅度有
关,与角两边的长短无关。
序号 是否正确 理由
③ √ 角的两边是两条具有公共端点的射线。
④ 平角是由顶点和两条边组成的图形,平角和直
线是两个不同的概念。
⑤ 周角的两条边重合成一条射线,周角和射线是
两个不同的概念。
1.角的度量单位:度、分、秒是角的基本度量单位。把周角等
分为360份,每一份就是 的角;把 的角等分成60份,每一
份就是1分,记作;把1分的角等分成60份,每一份就是1秒,
记作 。
2.角的单位换算:
, ;, ;
, ;1周角 ,1平角 。
它们之间的换算是60进制,这与时间的时、分、秒
之间的换算是一样的。
典例3 (1)把 转化为用度、分、秒表示的形式;
解: ;
(2)把 转化成用度表示的形式。
解: 。
知识过关
①角是由两条有公共 端点 的 射线 所组成的图形.这个
公共 端点 叫作这个角的 顶点 .角也可以看成是由一
条 射线 绕着它的 端点 旋转而成的图形.起始位置的
射线叫作角的 始边 ,终止位置的射线叫作角的 终边 .
②一个周角等于 360° ,一个平角等于 180° .
③1°= 60 ',1'= 60 ″;1″= ',1'= °.
端点
射线
端点
顶点
射线
端点
始边
终
边
360°
180°
60
60
角的概念及表示
1. 给出下列说法:①两条射线所组成的图形叫作角;②一条
射线旋转而成的图形叫作角;③两条具有公共端点的射线
组成的图形叫作角;④角是一条射线绕它的端点旋转形成
的图形.其中,正确的有( B )
A. 1个 B. 2个
C. 3个 D. 4个
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. 如图,能用∠1、∠EOF、∠O三种方法表示同一个角的
图形是( D )
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3. 下列关于平角和周角的说法正确的是( D )
A. 平角是一条线段
B. 周角是一条射线
C. 周角只有一条边
D. 反向延长射线OA,就形成一个平角
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. [母题 教材P179课内练习T1]如图,图中共有几个角?用
适当的方式表示这些角.
【解】图中共有6个角,分别是:∠1,∠DOB,
∠DOA,∠2,∠COA,∠3.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
角的度量
5. 如图所示,用量角器度量∠AOB,可以读出∠AOB的度
数为( B )
A. 45°
B. 55°
C. 125°
D. 135°
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
角的计算
6. [2024·金华期末]将20°30'转化为度的形式,即:20°30'
= °.
7. [2024·宁波月考]35.7°= ° '.
20.5
35
42
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(1)48°39'+67°31';
【解】48°39'+67°31'
=115°70'
=116°10';
8. 计算:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)23°53'×2-17°43'.
【解】23°53'×2-17°43'
=46°106'-17°43'
=29°63'
=30°3'.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
钟面角
9. [母题·教材P180作业题T1 2024·广西]如图,2时整,钟表
的时针和分针所成的锐角为( C )
A. 20°
B. 40°
C. 60°
D. 80°
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. 钟表上从早上6点30分到早上8点10分,时针所走的度数
为( B )
A. 45° B. 50°
C. 55° D. 60°
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. 图中角的表示方法正确的个数有( B )
A. 1个 B. 2个
C. 3个 D. 4个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
第一个图形应为∠CAB,表示不正确;第二个图形
∠AOB是平角,表示正确;第三个图形,直线与平角是
两个概念,平角有顶点,直线没有,表示不正确;第四
个图形,表示为∠CAB,正确.综上所述,表示正确的
有2个,故选B.
【答案】
B
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 已知∠α=30°18',∠β=30.18°,∠γ=30.3°,则
( B )
A. ∠α=∠β B. ∠α=∠γ
C. ∠β=∠γ D. 无法比较大小
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13. [2024·安庆期末]某同学晚上6点多开始做作业,他家墙上
时钟的时针和分针的夹角是120°,他做完作业后还是6
点多,且时针和分针的夹角还是120°,此同学做作业大
约用了 分钟.
44
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
设开始做作业时的时间是6点x分,
6x-0.5x=180-120,解得x≈11;
设做完作业后的时间是6点y分,
6y-0.5y=180+120,解得y≈55,
所以此同学做作业大约用了55-11=44(分钟).
【点拨】
分针速度是时针速度的12倍,分针一分钟走6°,对
应时针走0.5°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. 计算:
(1)11°23'26″×3;(结果用度、分、秒表示)
【解】11°23'26″×3=33°69'78″=34°10'18″;
(2)40°40'÷3;(结果用度、分、秒表示)
【解】40°40'÷3=39°99'60″÷3=13°33'20″;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(3)90°-79°18'6″;(结果用度、分、秒表示)
【解】90°-79°18'6″=89°59'60″-79°18'6″=
10°41'54″;
(4)24°13'37″+35°46'23″.(结果用度表示)
【解】24°13'37″+35°46'23″=59°59'60″=60°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. [新视角·规律探究题] 如图,观察图,回答下列问题:
(1)图①中有几个角?
【解】图①中有1个角;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)图②中有几个角?
【解】图②中有3个角;
(3)图③中有几个角?
【解】图③中有6个角;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(4)以此类推,如图④所示,若一个角内有n条射线,此
时共有多少个角?
【解】由前三问类推,角内有n条射线时,图中共有
(n+2)条射线,则角的个数为 .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
