6.7 角的和差 课件(共46张PPT)
文档属性
| 名称 | 6.7 角的和差 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 7.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 12:17:14 | ||
图片预览











文档简介
(共46张PPT)
6.7 角的和差
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
角的和差
课程目标
深入理解角的和差的概念,能结合具体图形清晰表述角的和差关系。
熟练掌握角的和差的计算方法,能根据图形中角的位置关系准确进行和差运算。
能综合运用角的和差与角平分线等知识解决较复杂的角的计算问题,提升几何思维能力。
角的和差的概念
角的和差与线段的和差类似,是基于角的位置关系产生的数量关系。
角的和:当一个角的两边分别是另外两个角的一边,且这个角的内部包含了另外两个角的内部,那么这个角的度数等于另外两个角的度数之和。简单来说,就是一个角可以看作是由两个较小的角 “拼接” 而成的。
几何表示:如图 1,射线\(OB\)在\(\angle AOC\)的内部,那么\(\angle AOC\)是\(\angle AOB\)和\(\angle BOC\)的和,记作\(\angle AOC=\angle AOB+\angle BOC\)。
角的差:当一个角是另一个较大的角的一部分时,这个角的度数等于较大角的度数减去剩余部分角的度数。即一个较大的角可以看作是由一个角 “减去” 另一个较小的角得到的。
几何表示:如图 1,因为\(\angle AOC=\angle AOB+\angle BOC\),所以\(\angle AOB=\angle AOC-\angle BOC\),\(\angle BOC=\angle AOC-\angle AOB\),这里\(\angle AOB\)和\(\angle BOC\)分别是\(\angle AOC\)与另一个角的差。
角的和差的几何意义
从几何图形上看,角的和差体现了角与角之间的包含关系:
角的和对应的图形中,两个较小的角共同组成了一个较大的角,且它们有公共的顶点和一条公共边,另一条边分别在较大角的两边上。
角的差对应的图形中,较小的角是较大角的一部分,它们有公共的顶点和一条公共边,较小角的另一条边在较大角的内部。
角的和差的计算方法
直接计算
已知两个角的度数以及它们的位置关系(能构成和或差),直接根据和差关系进行计算。
例 1:已知\(\angle 1 = 35 °\),\(\angle 2 = 45 °\),且\(\angle 1\)和\(\angle 2\)可以组成\(\angle 3\),求\(\angle 3\)的度数。
解:因为\(\angle 3\)是\(\angle 1\)和\(\angle 2\)的和,所以\(\angle 3=\angle 1+\angle 2 = 35 °+45 °=80 °\)。
例 2:已知\(\angle \alpha = 120 °\),\(\angle \beta = 50 °\),且\(\angle \beta\)是\(\angle \alpha\)的一部分,求\(\angle \alpha\)与\(\angle \beta\)的差。
解:\(\angle \alpha-\angle \beta=120 ° - 50 °=70 °\)。
结合图形计算
根据图形中角的位置关系,找出已知角和未知角之间的和差关系,再代入数据计算。
例 3:如图 2,已知\(\angle AOD = 150 °\),\(\angle AOB = \angle COD = 40 °\),求\(\angle BOC\)的度数。
解:由图可知\(\angle AOD=\angle AOB+\angle BOC+\angle COD\),所以\(\angle BOC=\angle AOD-\angle AOB-\angle COD=150 ° - 40 °-40 °=70 °\)。
例 4:如图 3,\(\angle AOB = 90 °\),\(\angle COD = 90 °\),\(\angle AOC = 20 °\),求\(\angle BOD\)的度数。
解:因为\(\angle AOB = 90 °\),所以\(\angle BOC=\angle AOB-\angle AOC=90 ° - 20 °=70 °\)。
又因为\(\angle COD = 90 °\),所以\(\angle BOD=\angle BOC+\angle COD=70 °+90 °=160 °\)。
角的和差与角平分线的综合计算
当题目中涉及角平分线时,可利用角平分线将角分成相等两部分的性质,结合角的和差进行计算。
例 5:如图 4,\(OC\)是\(\angle AOB\)的平分线,\(\angle AOD = 110 °\),\(\angle COD = 10 °\),求\(\angle AOB\)的度数。
解:因为\(\angle AOD=\angle AOC+\angle COD\),所以\(\angle AOC=\angle AOD-\angle COD=110 ° - 10 °=100 °\)。
又因为\(OC\)是\(\angle AOB\)的平分线,所以\(\angle AOB = 2\angle AOC=2 100 °=200 °\)(注意:大于 180° 的角也是存在的)。
例 6:如图 5,\(\angle AOB = 160 °\),\(OD\)是\(\angle AOC\)的平分线,\(OE\)是\(\angle BOC\)的平分线,求\(\angle DOE\)的度数。
解:因为\(OD\)平分\(\angle AOC\),所以\(\angle DOC=\frac{1}{2}\angle AOC\);因为\(OE\)平分\(\angle BOC\),所以\(\angle COE=\frac{1}{2}\angle BOC\)。
而\(\angle DOE=\angle DOC+\angle COE=\frac{1}{2}\angle AOC+\frac{1}{2}\angle BOC=\frac{1}{2}(\angle AOC+\angle BOC)=\frac{1}{2}\angle AOB\)。
代入\(\angle AOB = 160 °\),得\(\angle DOE=\frac{1}{2} 160 °=80 °\)。
角的和差的实际应用
角度测量:在实际测量中,当遇到无法直接测量的角时,可通过测量与之相关的两个角的度数,利用和差关系求出该角的度数。例如,测量一个不规则多边形的内角时,可将其分割成几个已知角,再通过和差计算。
天文观测:在观测天体的角度位置时,常常需要计算两个天体与观测点形成的角的和差,以确定它们之间的相对位置关系。
游戏设计:在一些涉及角度操作的游戏中,如射击游戏,需要计算枪口角度与目标角度的和差,以实现精准瞄准。
易错点提醒
计算角的和差时,要先确认角的位置关系是否满足和差条件,不能盲目相加或相减。
当角的度数涉及度、分、秒时,要注意单位统一,遵循 “满 60 进 1” 或 “借 1 当 60” 的原则进行换算。例如,计算\(30 °45 +25 °30 =55 °75 =56 °15 \);计算\(50 °10 -20 °30 =49 °70 -20 °30 =29 °40 \)。
利用角平分线解题时,要明确角平分线所分的是哪一个角,避免混淆。
课堂练习
已知\(\angle A = 50 °\),\(\angle B = 30 °\),求\(\angle A+\angle B\)和\(\angle A-\angle B\)的度数。
如图,\(\angle AOC = 130 °\),\(\angle BOC = 60 °\),求\(\angle AOB\)的度数。
\(OM\)是\(\angle AOB\)的平分线,\(\angle AOM = 35 °\),\(\angle BOC = 20 °\),求\(\angle AOC\)的度数(考虑\(OC\)在\(\angle AOB\)内部和外部两种情况)。
计算:
\(45 °20 +30 °50 \)
\(90 °-35 °40 \)
总结
角的和是指一个角由两个较小的角拼接而成,其度数为两个角的度数之和;角的差是指一个角为较大角减去一个较小角,其度数为两个角的度数之差。
计算角的和差时,要结合图形确定角的位置关系,明确和差关系后再代入计算,涉及角平分线时可利用其性质简化计算。
角的和差在实际测量、天文观测等领域有重要应用,计算时要注意单位换算和位置关系的判断,避免出错。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.会表示两个角的和差,会用量角器作两个角的和差。
2.理解角平分线的定义,能用角平分线解决有关问题。
3.会进行有关角的和、差、倍、分的简单计算。
概念 表示 图示
两个角 的和 如果一个角的度数是另 两个角的度数的和,那 么这个角就叫作另两个 角的和。 ________________________________
概念 表示 图示
两个角 的差 如果一个角的度数是另 两个角的度数的差,那 么这个角就叫作另两个 角的差。 ________________________________
典例1 据图回答下列问题:
(1)是哪两个角的和? 是哪两个角的和?
解:是与 的和,即
。
是与 的和,即
。
(2) 是哪两个角的差?
解:是与的差,
也是与 的差,
即 。
典例1 据图回答下列问题:
条件
图形 ________________
作法
角平分线:从一个角的顶点引出的一条射线,把这个角分成
两个相等的角,这条射线叫作这个角的平分线。
如图,射线是 的平分线。这时,
(或
)。
角的平分线是以这个角的顶点为端点的一
条射线。
教材延伸
角的三等分线
如图,射线,在的内部,如果
,那么射线,是 的三
等分线。类似地,从一个角的顶点出发,把这
个角分成个相等的角的射线,叫作这个角的 等分线,
如四等分线、五等分线等。
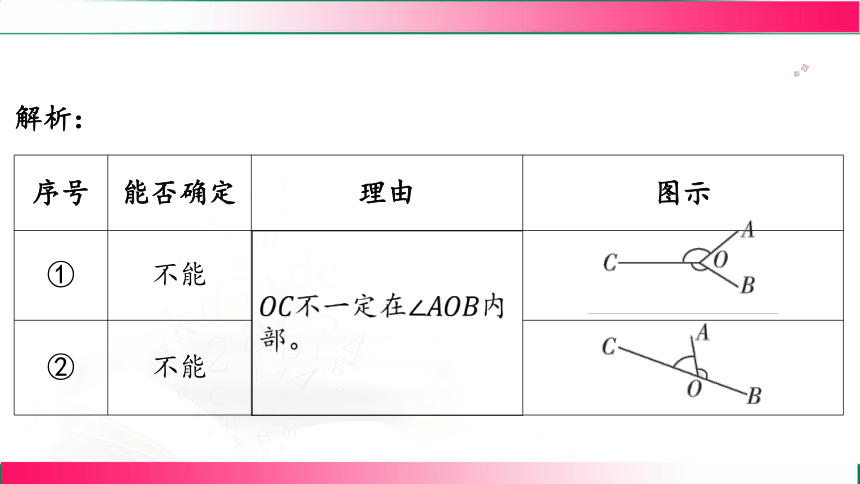
典例2 (易错题)已知三条不同的射线,, ,有下列条
件:; ;
; ;
。其中,能确定平分 的有
( )
C
A.3个 B.2个 C.1个 D.0个
解析:
序号 能否确定 理由 图示
① 不能 ______________________________________
② 不能 ______________________________________
序号 能否确定 理由 图示
③ 不能 ______________________________________
④ 不能 ___________________________________
序号 能否确定 理由 图示
⑤ 能 _____________________________
知识过关
①如果一个角的度数是另两个角的度数的 和 ,那么这个角
就叫作另两个角的和.
②如果一个角的度数是另两个角的度数的 差 ,那么这个角
就叫作另两个角的差.
③从一个角的顶点引出的一条射线,把这个角分成 两个相等
的角 ,这条射线叫作这个角的平分线.
和
差
两个相等
的角
角的和差
1. 如图所示,∠AOD-∠AOC=( D )
A. ∠AOC B. ∠BOC
C. ∠BOD D. ∠COD
(第1题)
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. 如图,已知∠AOC=∠BOD=70°,∠BOC=30°,
则∠AOD的度数为( B )
A. 100° B. 110°
C. 130° D. 140°
(第2题)
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3. [2024·扬州一模]将两块三角板如图叠放,若∠AOC=
∠BOD=90°,∠AOD=132°,则∠BOC
= .
(第3题)
48°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. [2024·杭州期末]如图,直线AB,CD交于点O,
∠AOC∶∠COE=1∶2,若∠BOE=96°,则∠AOD
= °.
(第4题)
152
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
因为∠AOC∶∠COE=1∶2,
所以设∠AOC=x°,∠COE=2x°.
因为∠AOC+∠COE+∠BOE=180°,
∠BOE=96°,
所以x°+2x°+96°=180°,
所以x=28,即∠AOC=28°,
所以∠AOD=180°-∠AOC=152°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5. 如图所示,已知∠α,∠β,且∠α,∠β均为锐角,求作
一个角,使它等于∠α与∠β的和.(尺规作图,不写作法,
保留痕迹)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】如答图所示,∠AOC即为所求.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
角的平分线
6. 如图,点A,B,C在同一条直线上,BD平分∠ABE,
∠EBC=40°,则∠ABD的度数为( C )
A. 50° B. 65°
C. 70° D. 75°
(第6题)
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 如图,∠AOB=60°,∠DOE=50°,OD,OE分别
平分∠AOB,∠AOC,则∠AOC= °.
(第7题)
40
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为OD,OE分别平分∠AOB,∠AOC,∠AOB
=60°,
所以∠AOE= ∠AOC,∠AOD= ∠AOB=
30°,
所以∠DOE=∠AOE+∠AOD= ∠AOC+30°.
因为∠DOE=50°,所以30°+ ∠AOC=50°,
所以∠AOC=40°.
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. 已知:如图,∠AOB=40°,在∠AOB的外部引射线
OC,使∠BOC=20°,再画出∠AOC的平分线OD.
(1)请借助直尺和量角器补全图形;
【解】如图.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求∠BOD的度数.
【解】因为∠AOB=40°,∠BOC=20°,所以∠AOC=∠AOB+∠BOC=60°.
因为OD平分∠AOC,
所以∠AOD= ∠AOC=30°,
所以∠BOD=∠AOB-∠AOD=10°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[易错题]角的位置未分类讨论而出错
9. 如图,∠AOB=50°,以O为端点画射线OC,使
∠BOC=20°,则∠AOC的度数为( D )
A. 30°
B. 70°
C. 50°
D. 30°或70°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
如图①所示,此时∠AOC=∠AOB-∠BOC=50°
-20°=30°;
D
如图②所示,此时∠AOC=∠AOB+∠BOC=50°
+20°=70°.
综上,∠AOC的度数为30°或70°.
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. [新考法·折叠法][2024·丽水期末] 如图,长方形ABCD
中,点E,F分别在边AB,BC上,连接DF,EF. 将
∠C沿DF折叠,点C落在点G处;将∠B沿EF折叠,
点B恰好落在FG的延长线上点H处.若∠BFE=
19°59',则∠CFD的度数是( A )
A. 70°1' B. 70°41'
C. 71°1' D. 71°41'
(第10题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
由折叠得到:∠BFE=∠HFE,∠CFD=
∠GFD.
又因为∠BFE+∠HFE+∠CFD+∠GFD=
180°,
所以∠BFE+∠CFD=90°.
因为∠BFE=19°59',
所以∠CFD=90°-19°59'=70°1'.
故选:A.
【答案】
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. [2024·绍兴越城区期末]如图,将两块三角尺的直角
∠AOB与∠COD的顶点O重合在一起,绕点O转动三
角尺AOB,使两块三角尺仍有部分重叠,且∠AOD=
3∠BOD,则∠AOC的度数为( B )
A. 30° B. 45°
C. 60° D. 75°
(第11题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
根据题意得:∠AOB=∠COD=90°,
所以∠AOD+∠BOC=∠AOC+∠BOC+
∠COD=∠AOB+∠COD=180°,∠AOB-∠BOC
=∠COD-∠BOC,
所以∠AOC=∠BOD.
因为∠AOD=3∠BOD,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以∠AOD=3∠AOC,
所以3∠AOC+∠BOC=180°,
所以2∠AOC+∠AOB=180°,
所以2∠AOC+90°=180°,
解得∠AOC=45°.
故选:B.
B
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 以∠AOB的顶点O为端点引射线OP,使
∠AOP∶∠BOP=3∶2,若∠AOB=20°,则∠AOP的
度数为 .
12°或60°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
如图①,当射线OP在∠AOB的内部时,设∠AOP
=3x,则∠BOP=2x,
所以∠AOB=∠AOP+∠BOP=5x=20°,
解得x=4°,所以∠AOP=12°;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
如图②,当射线OP在∠AOB的外部时,设∠AOP
=3y,则∠BOP=2y,
因为∠AOP=∠AOB+∠BOP,∠AOB=20°,
所以3y=20°+2y,解得y=20°,
所以∠AOP=60°.
故∠AOP的度数为12°或60°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13. [2023·湖州质检]如图所示,OB是∠AOC的平分线,
∠COD= ∠BOD,若∠COD=17°,则∠AOD的度
数是 .
(第13题)
85°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. [新趋势·跨学科]如图,一束光沿CD方向,先后经过平
面镜OB、OA反射后,沿EF方向射出,已知∠AOB=
120°,∠CDB=20°,则∠AEF= .
(第14题)
40°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为一束光沿CD方向,先后经过平面镜OB、OA
反射后,沿EF方向射出,所以∠EDO=∠CDB=
20°,∠AEF=∠OED. 在△ODE中,∠OED=
180°-∠AOB-∠EDO=180°-120°-20°=
40°,所以∠AEF=∠OED=40°.故答案为:40°.
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. 如图,AB为一条直线,OC是∠AOD的平分线.
(1)如图①,若∠COE为直角,且∠AOD=70°,则
∠BOE的度数是 ;
55°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为∠AOD=70°,OC是∠AOD的平分线,
所以∠AOC= ∠AOD=35°.
因为∠COE为直角,
所以∠COE=90°,
所以∠BOE=∠AOB-∠AOC-∠COE=
180°-35°-90°=55°;
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)如图②,若∠DOE∶∠BOD=2∶5,且∠COE=
80°,求∠BOE的度数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】因为∠DOE∶∠BOD=2∶5,所以设∠DOE=
2x,则∠BOD=5x,所以∠BOE=3x.
因为OC是∠AOD的平分线,∠COE=80°,
所以∠AOC=∠COD=80°-2x,
所以2(80°-2x)+5x=180°,解得x=20°,
所以∠BOE=3x=60°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看!
6.7 角的和差
第6章 图形的初步知识
【2025-2026学年】浙教版 数学 七年级上册
授课教师:********
班 级:********
时 间:********
角的和差
课程目标
深入理解角的和差的概念,能结合具体图形清晰表述角的和差关系。
熟练掌握角的和差的计算方法,能根据图形中角的位置关系准确进行和差运算。
能综合运用角的和差与角平分线等知识解决较复杂的角的计算问题,提升几何思维能力。
角的和差的概念
角的和差与线段的和差类似,是基于角的位置关系产生的数量关系。
角的和:当一个角的两边分别是另外两个角的一边,且这个角的内部包含了另外两个角的内部,那么这个角的度数等于另外两个角的度数之和。简单来说,就是一个角可以看作是由两个较小的角 “拼接” 而成的。
几何表示:如图 1,射线\(OB\)在\(\angle AOC\)的内部,那么\(\angle AOC\)是\(\angle AOB\)和\(\angle BOC\)的和,记作\(\angle AOC=\angle AOB+\angle BOC\)。
角的差:当一个角是另一个较大的角的一部分时,这个角的度数等于较大角的度数减去剩余部分角的度数。即一个较大的角可以看作是由一个角 “减去” 另一个较小的角得到的。
几何表示:如图 1,因为\(\angle AOC=\angle AOB+\angle BOC\),所以\(\angle AOB=\angle AOC-\angle BOC\),\(\angle BOC=\angle AOC-\angle AOB\),这里\(\angle AOB\)和\(\angle BOC\)分别是\(\angle AOC\)与另一个角的差。
角的和差的几何意义
从几何图形上看,角的和差体现了角与角之间的包含关系:
角的和对应的图形中,两个较小的角共同组成了一个较大的角,且它们有公共的顶点和一条公共边,另一条边分别在较大角的两边上。
角的差对应的图形中,较小的角是较大角的一部分,它们有公共的顶点和一条公共边,较小角的另一条边在较大角的内部。
角的和差的计算方法
直接计算
已知两个角的度数以及它们的位置关系(能构成和或差),直接根据和差关系进行计算。
例 1:已知\(\angle 1 = 35 °\),\(\angle 2 = 45 °\),且\(\angle 1\)和\(\angle 2\)可以组成\(\angle 3\),求\(\angle 3\)的度数。
解:因为\(\angle 3\)是\(\angle 1\)和\(\angle 2\)的和,所以\(\angle 3=\angle 1+\angle 2 = 35 °+45 °=80 °\)。
例 2:已知\(\angle \alpha = 120 °\),\(\angle \beta = 50 °\),且\(\angle \beta\)是\(\angle \alpha\)的一部分,求\(\angle \alpha\)与\(\angle \beta\)的差。
解:\(\angle \alpha-\angle \beta=120 ° - 50 °=70 °\)。
结合图形计算
根据图形中角的位置关系,找出已知角和未知角之间的和差关系,再代入数据计算。
例 3:如图 2,已知\(\angle AOD = 150 °\),\(\angle AOB = \angle COD = 40 °\),求\(\angle BOC\)的度数。
解:由图可知\(\angle AOD=\angle AOB+\angle BOC+\angle COD\),所以\(\angle BOC=\angle AOD-\angle AOB-\angle COD=150 ° - 40 °-40 °=70 °\)。
例 4:如图 3,\(\angle AOB = 90 °\),\(\angle COD = 90 °\),\(\angle AOC = 20 °\),求\(\angle BOD\)的度数。
解:因为\(\angle AOB = 90 °\),所以\(\angle BOC=\angle AOB-\angle AOC=90 ° - 20 °=70 °\)。
又因为\(\angle COD = 90 °\),所以\(\angle BOD=\angle BOC+\angle COD=70 °+90 °=160 °\)。
角的和差与角平分线的综合计算
当题目中涉及角平分线时,可利用角平分线将角分成相等两部分的性质,结合角的和差进行计算。
例 5:如图 4,\(OC\)是\(\angle AOB\)的平分线,\(\angle AOD = 110 °\),\(\angle COD = 10 °\),求\(\angle AOB\)的度数。
解:因为\(\angle AOD=\angle AOC+\angle COD\),所以\(\angle AOC=\angle AOD-\angle COD=110 ° - 10 °=100 °\)。
又因为\(OC\)是\(\angle AOB\)的平分线,所以\(\angle AOB = 2\angle AOC=2 100 °=200 °\)(注意:大于 180° 的角也是存在的)。
例 6:如图 5,\(\angle AOB = 160 °\),\(OD\)是\(\angle AOC\)的平分线,\(OE\)是\(\angle BOC\)的平分线,求\(\angle DOE\)的度数。
解:因为\(OD\)平分\(\angle AOC\),所以\(\angle DOC=\frac{1}{2}\angle AOC\);因为\(OE\)平分\(\angle BOC\),所以\(\angle COE=\frac{1}{2}\angle BOC\)。
而\(\angle DOE=\angle DOC+\angle COE=\frac{1}{2}\angle AOC+\frac{1}{2}\angle BOC=\frac{1}{2}(\angle AOC+\angle BOC)=\frac{1}{2}\angle AOB\)。
代入\(\angle AOB = 160 °\),得\(\angle DOE=\frac{1}{2} 160 °=80 °\)。
角的和差的实际应用
角度测量:在实际测量中,当遇到无法直接测量的角时,可通过测量与之相关的两个角的度数,利用和差关系求出该角的度数。例如,测量一个不规则多边形的内角时,可将其分割成几个已知角,再通过和差计算。
天文观测:在观测天体的角度位置时,常常需要计算两个天体与观测点形成的角的和差,以确定它们之间的相对位置关系。
游戏设计:在一些涉及角度操作的游戏中,如射击游戏,需要计算枪口角度与目标角度的和差,以实现精准瞄准。
易错点提醒
计算角的和差时,要先确认角的位置关系是否满足和差条件,不能盲目相加或相减。
当角的度数涉及度、分、秒时,要注意单位统一,遵循 “满 60 进 1” 或 “借 1 当 60” 的原则进行换算。例如,计算\(30 °45 +25 °30 =55 °75 =56 °15 \);计算\(50 °10 -20 °30 =49 °70 -20 °30 =29 °40 \)。
利用角平分线解题时,要明确角平分线所分的是哪一个角,避免混淆。
课堂练习
已知\(\angle A = 50 °\),\(\angle B = 30 °\),求\(\angle A+\angle B\)和\(\angle A-\angle B\)的度数。
如图,\(\angle AOC = 130 °\),\(\angle BOC = 60 °\),求\(\angle AOB\)的度数。
\(OM\)是\(\angle AOB\)的平分线,\(\angle AOM = 35 °\),\(\angle BOC = 20 °\),求\(\angle AOC\)的度数(考虑\(OC\)在\(\angle AOB\)内部和外部两种情况)。
计算:
\(45 °20 +30 °50 \)
\(90 °-35 °40 \)
总结
角的和是指一个角由两个较小的角拼接而成,其度数为两个角的度数之和;角的差是指一个角为较大角减去一个较小角,其度数为两个角的度数之差。
计算角的和差时,要结合图形确定角的位置关系,明确和差关系后再代入计算,涉及角平分线时可利用其性质简化计算。
角的和差在实际测量、天文观测等领域有重要应用,计算时要注意单位换算和位置关系的判断,避免出错。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
学习目录
1
复习引入
2
新知讲解
3
典例讲解
1.会表示两个角的和差,会用量角器作两个角的和差。
2.理解角平分线的定义,能用角平分线解决有关问题。
3.会进行有关角的和、差、倍、分的简单计算。
概念 表示 图示
两个角 的和 如果一个角的度数是另 两个角的度数的和,那 么这个角就叫作另两个 角的和。 ________________________________
概念 表示 图示
两个角 的差 如果一个角的度数是另 两个角的度数的差,那 么这个角就叫作另两个 角的差。 ________________________________
典例1 据图回答下列问题:
(1)是哪两个角的和? 是哪两个角的和?
解:是与 的和,即
。
是与 的和,即
。
(2) 是哪两个角的差?
解:是与的差,
也是与 的差,
即 。
典例1 据图回答下列问题:
条件
图形 ________________
作法
角平分线:从一个角的顶点引出的一条射线,把这个角分成
两个相等的角,这条射线叫作这个角的平分线。
如图,射线是 的平分线。这时,
(或
)。
角的平分线是以这个角的顶点为端点的一
条射线。
教材延伸
角的三等分线
如图,射线,在的内部,如果
,那么射线,是 的三
等分线。类似地,从一个角的顶点出发,把这
个角分成个相等的角的射线,叫作这个角的 等分线,
如四等分线、五等分线等。
典例2 (易错题)已知三条不同的射线,, ,有下列条
件:; ;
; ;
。其中,能确定平分 的有
( )
C
A.3个 B.2个 C.1个 D.0个
解析:
序号 能否确定 理由 图示
① 不能 ______________________________________
② 不能 ______________________________________
序号 能否确定 理由 图示
③ 不能 ______________________________________
④ 不能 ___________________________________
序号 能否确定 理由 图示
⑤ 能 _____________________________
知识过关
①如果一个角的度数是另两个角的度数的 和 ,那么这个角
就叫作另两个角的和.
②如果一个角的度数是另两个角的度数的 差 ,那么这个角
就叫作另两个角的差.
③从一个角的顶点引出的一条射线,把这个角分成 两个相等
的角 ,这条射线叫作这个角的平分线.
和
差
两个相等
的角
角的和差
1. 如图所示,∠AOD-∠AOC=( D )
A. ∠AOC B. ∠BOC
C. ∠BOD D. ∠COD
(第1题)
D
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
2. 如图,已知∠AOC=∠BOD=70°,∠BOC=30°,
则∠AOD的度数为( B )
A. 100° B. 110°
C. 130° D. 140°
(第2题)
B
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
3. [2024·扬州一模]将两块三角板如图叠放,若∠AOC=
∠BOD=90°,∠AOD=132°,则∠BOC
= .
(第3题)
48°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
4. [2024·杭州期末]如图,直线AB,CD交于点O,
∠AOC∶∠COE=1∶2,若∠BOE=96°,则∠AOD
= °.
(第4题)
152
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
因为∠AOC∶∠COE=1∶2,
所以设∠AOC=x°,∠COE=2x°.
因为∠AOC+∠COE+∠BOE=180°,
∠BOE=96°,
所以x°+2x°+96°=180°,
所以x=28,即∠AOC=28°,
所以∠AOD=180°-∠AOC=152°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
5. 如图所示,已知∠α,∠β,且∠α,∠β均为锐角,求作
一个角,使它等于∠α与∠β的和.(尺规作图,不写作法,
保留痕迹)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】如答图所示,∠AOC即为所求.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
角的平分线
6. 如图,点A,B,C在同一条直线上,BD平分∠ABE,
∠EBC=40°,则∠ABD的度数为( C )
A. 50° B. 65°
C. 70° D. 75°
(第6题)
C
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
7. 如图,∠AOB=60°,∠DOE=50°,OD,OE分别
平分∠AOB,∠AOC,则∠AOC= °.
(第7题)
40
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为OD,OE分别平分∠AOB,∠AOC,∠AOB
=60°,
所以∠AOE= ∠AOC,∠AOD= ∠AOB=
30°,
所以∠DOE=∠AOE+∠AOD= ∠AOC+30°.
因为∠DOE=50°,所以30°+ ∠AOC=50°,
所以∠AOC=40°.
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
8. 已知:如图,∠AOB=40°,在∠AOB的外部引射线
OC,使∠BOC=20°,再画出∠AOC的平分线OD.
(1)请借助直尺和量角器补全图形;
【解】如图.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)求∠BOD的度数.
【解】因为∠AOB=40°,∠BOC=20°,所以∠AOC=∠AOB+∠BOC=60°.
因为OD平分∠AOC,
所以∠AOD= ∠AOC=30°,
所以∠BOD=∠AOB-∠AOD=10°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
[易错题]角的位置未分类讨论而出错
9. 如图,∠AOB=50°,以O为端点画射线OC,使
∠BOC=20°,则∠AOC的度数为( D )
A. 30°
B. 70°
C. 50°
D. 30°或70°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
如图①所示,此时∠AOC=∠AOB-∠BOC=50°
-20°=30°;
D
如图②所示,此时∠AOC=∠AOB+∠BOC=50°
+20°=70°.
综上,∠AOC的度数为30°或70°.
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
10. [新考法·折叠法][2024·丽水期末] 如图,长方形ABCD
中,点E,F分别在边AB,BC上,连接DF,EF. 将
∠C沿DF折叠,点C落在点G处;将∠B沿EF折叠,
点B恰好落在FG的延长线上点H处.若∠BFE=
19°59',则∠CFD的度数是( A )
A. 70°1' B. 70°41'
C. 71°1' D. 71°41'
(第10题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
由折叠得到:∠BFE=∠HFE,∠CFD=
∠GFD.
又因为∠BFE+∠HFE+∠CFD+∠GFD=
180°,
所以∠BFE+∠CFD=90°.
因为∠BFE=19°59',
所以∠CFD=90°-19°59'=70°1'.
故选:A.
【答案】
A
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
11. [2024·绍兴越城区期末]如图,将两块三角尺的直角
∠AOB与∠COD的顶点O重合在一起,绕点O转动三
角尺AOB,使两块三角尺仍有部分重叠,且∠AOD=
3∠BOD,则∠AOC的度数为( B )
A. 30° B. 45°
C. 60° D. 75°
(第11题)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
根据题意得:∠AOB=∠COD=90°,
所以∠AOD+∠BOC=∠AOC+∠BOC+
∠COD=∠AOB+∠COD=180°,∠AOB-∠BOC
=∠COD-∠BOC,
所以∠AOC=∠BOD.
因为∠AOD=3∠BOD,
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以∠AOD=3∠AOC,
所以3∠AOC+∠BOC=180°,
所以2∠AOC+∠AOB=180°,
所以2∠AOC+90°=180°,
解得∠AOC=45°.
故选:B.
B
【答案】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
12. 以∠AOB的顶点O为端点引射线OP,使
∠AOP∶∠BOP=3∶2,若∠AOB=20°,则∠AOP的
度数为 .
12°或60°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【点拨】
如图①,当射线OP在∠AOB的内部时,设∠AOP
=3x,则∠BOP=2x,
所以∠AOB=∠AOP+∠BOP=5x=20°,
解得x=4°,所以∠AOP=12°;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
如图②,当射线OP在∠AOB的外部时,设∠AOP
=3y,则∠BOP=2y,
因为∠AOP=∠AOB+∠BOP,∠AOB=20°,
所以3y=20°+2y,解得y=20°,
所以∠AOP=60°.
故∠AOP的度数为12°或60°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
13. [2023·湖州质检]如图所示,OB是∠AOC的平分线,
∠COD= ∠BOD,若∠COD=17°,则∠AOD的度
数是 .
(第13题)
85°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
14. [新趋势·跨学科]如图,一束光沿CD方向,先后经过平
面镜OB、OA反射后,沿EF方向射出,已知∠AOB=
120°,∠CDB=20°,则∠AEF= .
(第14题)
40°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为一束光沿CD方向,先后经过平面镜OB、OA
反射后,沿EF方向射出,所以∠EDO=∠CDB=
20°,∠AEF=∠OED. 在△ODE中,∠OED=
180°-∠AOB-∠EDO=180°-120°-20°=
40°,所以∠AEF=∠OED=40°.故答案为:40°.
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
15. 如图,AB为一条直线,OC是∠AOD的平分线.
(1)如图①,若∠COE为直角,且∠AOD=70°,则
∠BOE的度数是 ;
55°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为∠AOD=70°,OC是∠AOD的平分线,
所以∠AOC= ∠AOD=35°.
因为∠COE为直角,
所以∠COE=90°,
所以∠BOE=∠AOB-∠AOC-∠COE=
180°-35°-90°=55°;
【点拨】
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
(2)如图②,若∠DOE∶∠BOD=2∶5,且∠COE=
80°,求∠BOE的度数.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
【解】因为∠DOE∶∠BOD=2∶5,所以设∠DOE=
2x,则∠BOD=5x,所以∠BOE=3x.
因为OC是∠AOD的平分线,∠COE=80°,
所以∠AOC=∠COD=80°-2x,
所以2(80°-2x)+5x=180°,解得x=20°,
所以∠BOE=3x=60°.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
谢谢观看!
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
