5.2认识函数(1) 课件(共25张PPT)
文档属性
| 名称 | 5.2认识函数(1) 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-14 12:19:43 | ||
图片预览





文档简介
(共25张PPT)
浙教版八年级上册
5.2 认识函数(1)
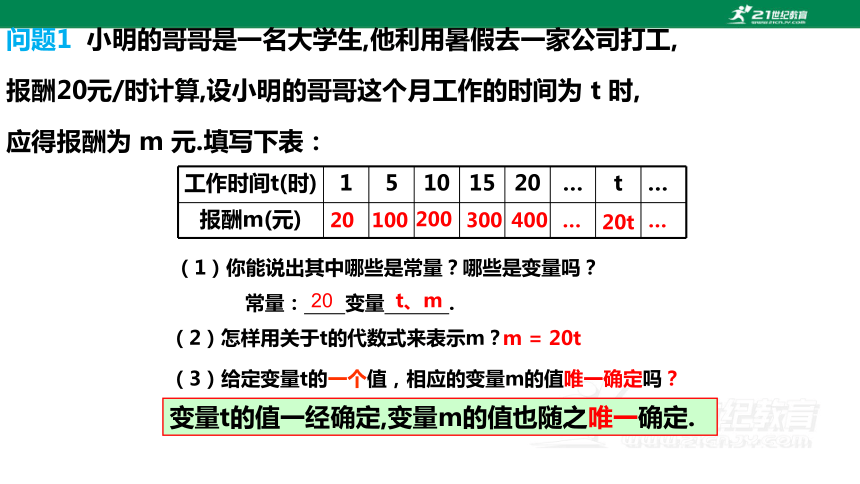
问题1 小明的哥哥是一名大学生,他利用暑假去一家公司打工,
报酬20元/时计算,设小明的哥哥这个月工作的时间为 t 时,
应得报酬为 m 元.填写下表:
(2)怎样用关于t的代数式来表示m?
工作时间t(时) 1 5 10 15 20 … t …
报酬m(元)
20t
100
400
300
200
20
m = 20t
(1)你能说出其中哪些是常量?哪些是变量吗?
(3)给定变量t的一个值,相应的变量m的值唯一确定吗?
…
…
常量: 变量 .
20
t、m
变量t的值一经确定,变量m的值也随之唯一确定.
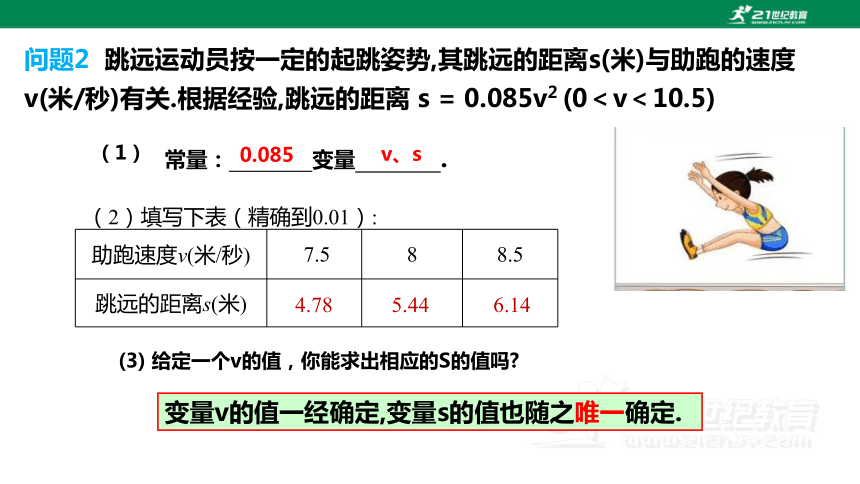
问题2 跳远运动员按一定的起跳姿势,其跳远的距离s(米)与助跑的速度
v(米/秒)有关.根据经验,跳远的距离 s = 0.085v2 (0<v<10.5)
(3) 给定一个v的值,你能求出相应的S的值吗
(1)
常量: 变量 .
0.085
v、s
变量v的值一经确定,变量s的值也随之唯一确定.
(2)填写下表(精确到0.01):
助跑速度v(米/秒) 7.5 8 8.5
跳远的距离s(米)
4.78
6.14
5.44
y=12 -
y=
问题3
x 0.2 0.4 0.6 0.8 …
0.3
0.35
0.4
0.45
变量x的值一经确定,变量y的值也随之唯一确定.
问题1:变量t 的值一经确定,变量m的值也随之唯一确定.
问题2:变量v 的值一经确定,变量s的值也随之唯一确定.
问题3:变量x 的值一经确定,变量y的值也随之唯一确定.
共同特点:
都有两个变量,给定其中某一个变量的值,
相应地就确定了另一个变量的值.
一般地,在某个变化过程中,设有两个变量x和y,
如果对于x的每一个确定的值,y都有唯一确定的值,
那么就说y是x的函数,x叫做自变量.
例如,上面的问题中,m是t的函数,t是自变量;
s是v的函数,v是自变量:y是x的函数,x是自变量.
这几个函数用等式来表示,这种表示函数关系的等式,叫做函数表达式,简称函数式。
用函数表达式表示函数的方法也叫解析法.
m=20t
s=0.085v2
y =x+
写几个不同类型的函数表达式
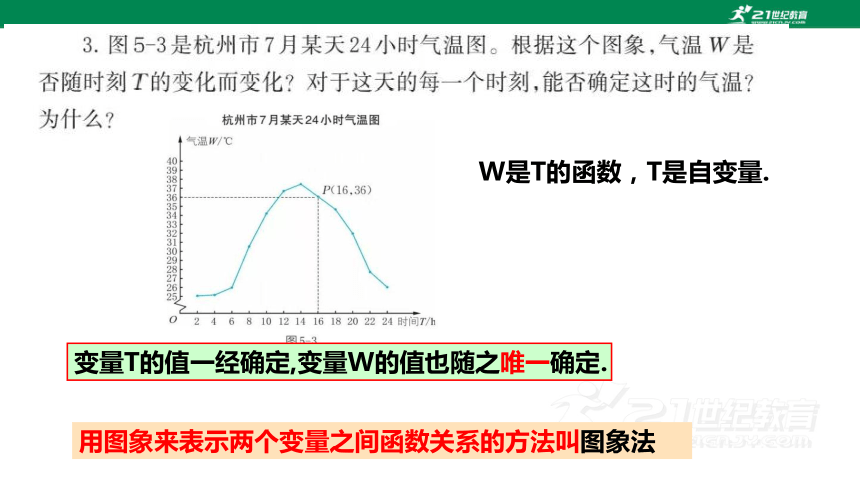
变量T的值一经确定,变量W的值也随之唯一确定.
W是T的函数,T是自变量.
用图象来表示两个变量之间函数关系的方法叫图象法
如下表是一年内某城市月份与相应的平均气温.
查一查
用列表法求函数值,只要查表得到.
当x=5时,函数值为 .
20.2
当x=3时,T= ;
y=9.3叫做当自变量x=3时的函数值.
9.3
把自变量x的一系列值和函数y对应值列成一个表.
这种表示函数关系的方法是列表法.
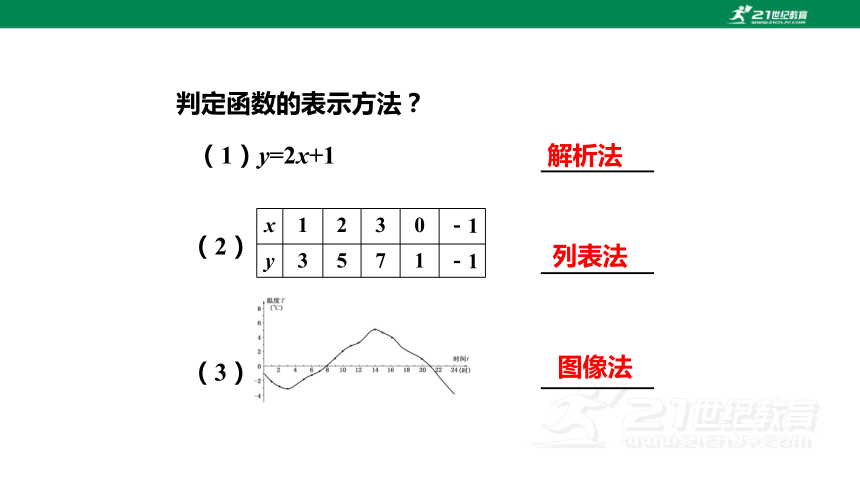
判定函数的表示方法?
(1)y=2x+1
解析法
列表法
图像法
x 1 2 3 0 -1
y 3 5 7 1 -1
(2)
(3)
③这里是用________ 法表示函数的.
列表
图象
解析
①上图是用________ 法表示函数的;
②右图是用________ 法表示函数的;
100t
t / h 1 2 3 4 5 t
S / km
100t
如果汽车的平均速度是100km/h
用含t 的代数式表示为:s= _____
100
200
300
400
500
在某一变化过程中,可以取不同数值的量,叫做变量.在某一变化过程中,取值始终保持不变的量,叫做常量.常量与变量函 数如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数.归纳总结:在一个变化过程中,主动引起变化的量叫做自变量,被动引起变化的量叫做因变量,始终没有变化的量叫做常量注意:函数指的是两个变量之间的一种关系。
判断两个变量是否具有函数关系,不仅看它们是否具有关系式存在,
更重要的是看对于x的每一个确定的值,y是否有唯一的值与它对应.
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
函数的表示方法:
1.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出函数的解析式.
(1)改变正方形的边长x,正方形的面积S随之改变.
S=x2
自变量
自变量的函数
(2)每分钟向一水池注水0.1m3,注水量y(单位:m3)随注水时间x(单位:min)的变化而变化.
y=0.1x
自变量
自变量的函数
夯实基础,稳扎稳打
2. 某市民用电费的价格是0.538元/千瓦时.设用电量为x千瓦·时,应付电费为y元,
(1)求y关于x的函数解析式.
(2)当x=40时,函数值是多少?
它的实际意义是什么?
y=0.538x
当x=40时,y=0.53x=0.538×40=21.52(元)
用40千瓦时电需付电费21.52元
用解析式求函数值,只要代入求值.
代一代
(3)若某用户的用电量为65千瓦·时,则该用户应付电费为多少元?
0.538×65=34.97(元)
3.如图,图象表示骑车时热量消耗 W (焦)与身体质量x (千克)之间的关系.
P的坐标为( )
当x=30时,W= ;
W=252叫做当自变量x=30时的函数值.
30,252
252
用图象法求函数值,只用找到相对应的坐标.
因为对于X的每一个值,W都有唯一确定的值与它对应,所以W是X的函数.
当x=50时,函数值为 .
399
身体质量 x (千克)
活动时消耗的热量W (焦)
p
课堂练习
4.已知△ABC的底边BC上的高线长是6cm。当BC的长改变时,三角形的面积也将改变.
(1)若△ABC的底边BC的长为x(cm),
则△ABC的面积y(cm2)可表示为 .
(2)当底边长从12cm变化到3cm时,
三角形的面积从 cm2变化到 cm2.
(1)y=3x (2)36 9
5.判断下列变量之间是否具有函数关系,并说明理由.
(1)y=x;(2); (3);(4)
看对于任意确定的一个 x 值,y 是否都有唯一确定的一个值与其对应,
若不是则不具有函数关系.
解析:(1)(3)不具有函数关系,例如:当 x=1 时,(1)中 y =1和 y = -1;(3)中 y = 和 y =-.
(2)(4)具有函数关系,因为每当 x 确定一个值时,y 就有唯一确定的值与其对应.
连续递推,豁然开朗
x
y
对于x的每一个确定的值,y都有唯一确定的
值与之对应,所以y是x的函数.
6.下列图象关系中,y是x的函数吗?
P( x ,y )
x
y
7.下列各图中,x是自变量,则y是x的函数吗?为什么?
y是x的函数
y不是x的函数
判断一个变量是否是另一个变量的函数,关键是看当自变量确定时,因变量是否有唯一确定的值与它对应.
┓
┓
P1
P2
x
y1
y2
8.下列各曲线中不能表示y是x的函数的是 ( )
A. B.
C. D.
D
一对三
9.下列图象关系中,y是x的函数吗?
对于x的每一个确定的值,y有两个值与之对应,
所以y不是x的函数.
x
y
P1
P2
x
y1
y2
10
40
80
148
250
确定
可以
125万m3
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
浙教版八年级上册
5.2 认识函数(1)
问题1 小明的哥哥是一名大学生,他利用暑假去一家公司打工,
报酬20元/时计算,设小明的哥哥这个月工作的时间为 t 时,
应得报酬为 m 元.填写下表:
(2)怎样用关于t的代数式来表示m?
工作时间t(时) 1 5 10 15 20 … t …
报酬m(元)
20t
100
400
300
200
20
m = 20t
(1)你能说出其中哪些是常量?哪些是变量吗?
(3)给定变量t的一个值,相应的变量m的值唯一确定吗?
…
…
常量: 变量 .
20
t、m
变量t的值一经确定,变量m的值也随之唯一确定.
问题2 跳远运动员按一定的起跳姿势,其跳远的距离s(米)与助跑的速度
v(米/秒)有关.根据经验,跳远的距离 s = 0.085v2 (0<v<10.5)
(3) 给定一个v的值,你能求出相应的S的值吗
(1)
常量: 变量 .
0.085
v、s
变量v的值一经确定,变量s的值也随之唯一确定.
(2)填写下表(精确到0.01):
助跑速度v(米/秒) 7.5 8 8.5
跳远的距离s(米)
4.78
6.14
5.44
y=12 -
y=
问题3
x 0.2 0.4 0.6 0.8 …
0.3
0.35
0.4
0.45
变量x的值一经确定,变量y的值也随之唯一确定.
问题1:变量t 的值一经确定,变量m的值也随之唯一确定.
问题2:变量v 的值一经确定,变量s的值也随之唯一确定.
问题3:变量x 的值一经确定,变量y的值也随之唯一确定.
共同特点:
都有两个变量,给定其中某一个变量的值,
相应地就确定了另一个变量的值.
一般地,在某个变化过程中,设有两个变量x和y,
如果对于x的每一个确定的值,y都有唯一确定的值,
那么就说y是x的函数,x叫做自变量.
例如,上面的问题中,m是t的函数,t是自变量;
s是v的函数,v是自变量:y是x的函数,x是自变量.
这几个函数用等式来表示,这种表示函数关系的等式,叫做函数表达式,简称函数式。
用函数表达式表示函数的方法也叫解析法.
m=20t
s=0.085v2
y =x+
写几个不同类型的函数表达式
变量T的值一经确定,变量W的值也随之唯一确定.
W是T的函数,T是自变量.
用图象来表示两个变量之间函数关系的方法叫图象法
如下表是一年内某城市月份与相应的平均气温.
查一查
用列表法求函数值,只要查表得到.
当x=5时,函数值为 .
20.2
当x=3时,T= ;
y=9.3叫做当自变量x=3时的函数值.
9.3
把自变量x的一系列值和函数y对应值列成一个表.
这种表示函数关系的方法是列表法.
判定函数的表示方法?
(1)y=2x+1
解析法
列表法
图像法
x 1 2 3 0 -1
y 3 5 7 1 -1
(2)
(3)
③这里是用________ 法表示函数的.
列表
图象
解析
①上图是用________ 法表示函数的;
②右图是用________ 法表示函数的;
100t
t / h 1 2 3 4 5 t
S / km
100t
如果汽车的平均速度是100km/h
用含t 的代数式表示为:s= _____
100
200
300
400
500
在某一变化过程中,可以取不同数值的量,叫做变量.在某一变化过程中,取值始终保持不变的量,叫做常量.常量与变量函 数如果在一个变化过程中,有两个变量x与y,对于x的每一个确定的值,y都有惟一的值与之对应,我们就说x是自变量,y是因变量,y是x的函数.归纳总结:在一个变化过程中,主动引起变化的量叫做自变量,被动引起变化的量叫做因变量,始终没有变化的量叫做常量注意:函数指的是两个变量之间的一种关系。
判断两个变量是否具有函数关系,不仅看它们是否具有关系式存在,
更重要的是看对于x的每一个确定的值,y是否有唯一的值与它对应.
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
函数的表示方法:
1.下列问题中哪些量是自变量?哪些量是自变量的函数?试写出函数的解析式.
(1)改变正方形的边长x,正方形的面积S随之改变.
S=x2
自变量
自变量的函数
(2)每分钟向一水池注水0.1m3,注水量y(单位:m3)随注水时间x(单位:min)的变化而变化.
y=0.1x
自变量
自变量的函数
夯实基础,稳扎稳打
2. 某市民用电费的价格是0.538元/千瓦时.设用电量为x千瓦·时,应付电费为y元,
(1)求y关于x的函数解析式.
(2)当x=40时,函数值是多少?
它的实际意义是什么?
y=0.538x
当x=40时,y=0.53x=0.538×40=21.52(元)
用40千瓦时电需付电费21.52元
用解析式求函数值,只要代入求值.
代一代
(3)若某用户的用电量为65千瓦·时,则该用户应付电费为多少元?
0.538×65=34.97(元)
3.如图,图象表示骑车时热量消耗 W (焦)与身体质量x (千克)之间的关系.
P的坐标为( )
当x=30时,W= ;
W=252叫做当自变量x=30时的函数值.
30,252
252
用图象法求函数值,只用找到相对应的坐标.
因为对于X的每一个值,W都有唯一确定的值与它对应,所以W是X的函数.
当x=50时,函数值为 .
399
身体质量 x (千克)
活动时消耗的热量W (焦)
p
课堂练习
4.已知△ABC的底边BC上的高线长是6cm。当BC的长改变时,三角形的面积也将改变.
(1)若△ABC的底边BC的长为x(cm),
则△ABC的面积y(cm2)可表示为 .
(2)当底边长从12cm变化到3cm时,
三角形的面积从 cm2变化到 cm2.
(1)y=3x (2)36 9
5.判断下列变量之间是否具有函数关系,并说明理由.
(1)y=x;(2); (3);(4)
看对于任意确定的一个 x 值,y 是否都有唯一确定的一个值与其对应,
若不是则不具有函数关系.
解析:(1)(3)不具有函数关系,例如:当 x=1 时,(1)中 y =1和 y = -1;(3)中 y = 和 y =-.
(2)(4)具有函数关系,因为每当 x 确定一个值时,y 就有唯一确定的值与其对应.
连续递推,豁然开朗
x
y
对于x的每一个确定的值,y都有唯一确定的
值与之对应,所以y是x的函数.
6.下列图象关系中,y是x的函数吗?
P( x ,y )
x
y
7.下列各图中,x是自变量,则y是x的函数吗?为什么?
y是x的函数
y不是x的函数
判断一个变量是否是另一个变量的函数,关键是看当自变量确定时,因变量是否有唯一确定的值与它对应.
┓
┓
P1
P2
x
y1
y2
8.下列各曲线中不能表示y是x的函数的是 ( )
A. B.
C. D.
D
一对三
9.下列图象关系中,y是x的函数吗?
对于x的每一个确定的值,y有两个值与之对应,
所以y不是x的函数.
x
y
P1
P2
x
y1
y2
10
40
80
148
250
确定
可以
125万m3
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
