4.3.1 坐标平面内图形的轴对称和平移 教案
文档属性
| 名称 | 4.3.1 坐标平面内图形的轴对称和平移 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 479.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-10-17 11:02:26 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
分课时教学设计
第4课时《4.3.1 坐标平面内图形的轴对称和平移》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 本节课的主要内容是让学生共同探究,动手操作,通过作图感受坐标平面内图形变化相应的坐标变化,要求学生利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形.本节课内容是在学生学习了轴对称及平面坐标直角系之后进行学习的,为学生探究坐标平面内图形的轴对称奠定了基础。为后续学习图形的变化打好基础,在教材中有着非常重要的地位和作用.
学习者分析 学生具有一定的数形结合意识,且经过一年的初中学习,学生已经具备了初步的逻辑推理能力、空间学习能力及自主学习能力,教师可以多为学生创造自主学习、共同探究的机会,通过动手画图探究坐标轴对称的两个点的坐标关系,使学生获得作轴对称图形的数学活动经验.
教学目标 掌握关于坐标轴对称的两个点的坐标的特点; 2.能在坐标系中作轴对称图形.
教学重点 关于坐标轴对称的两个点之间的坐标关系.
教学难点 利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形的过程比较复杂,是本节教学的难点.
学习活动设计
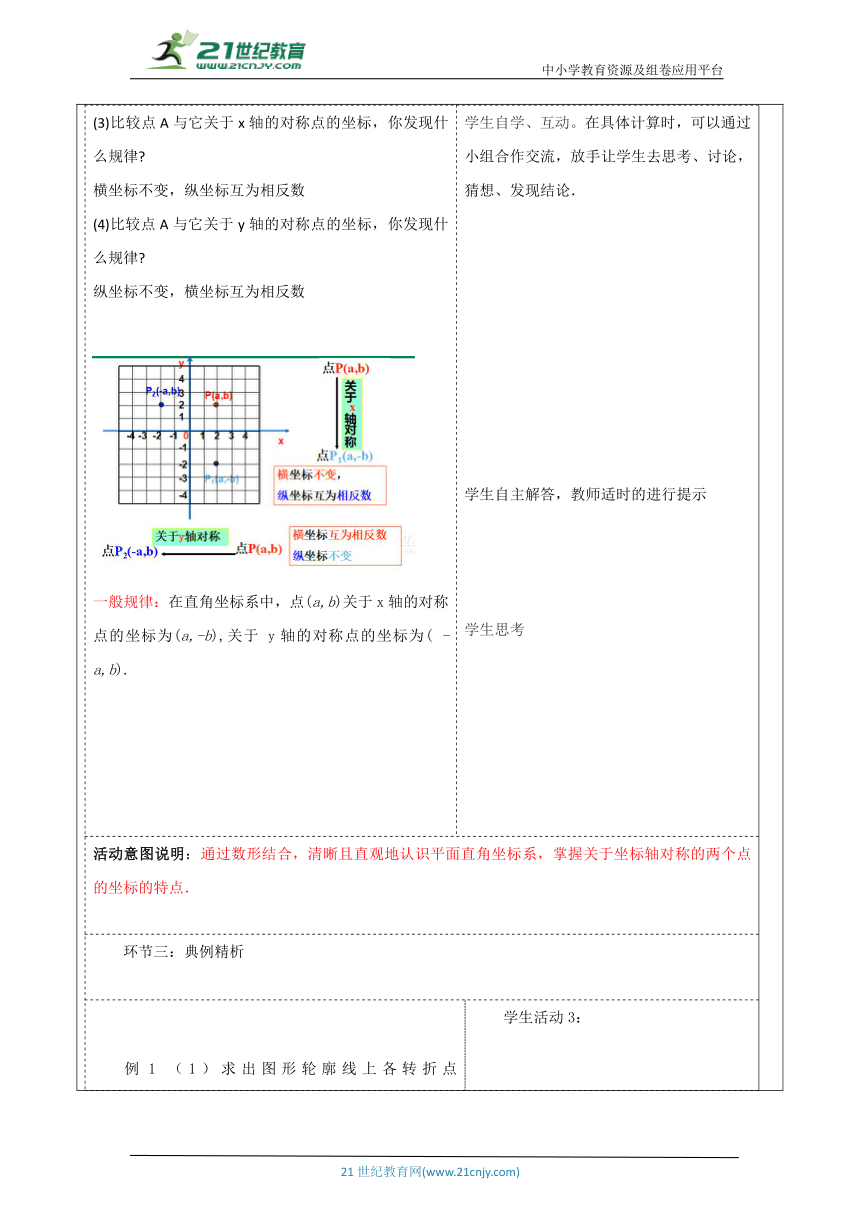
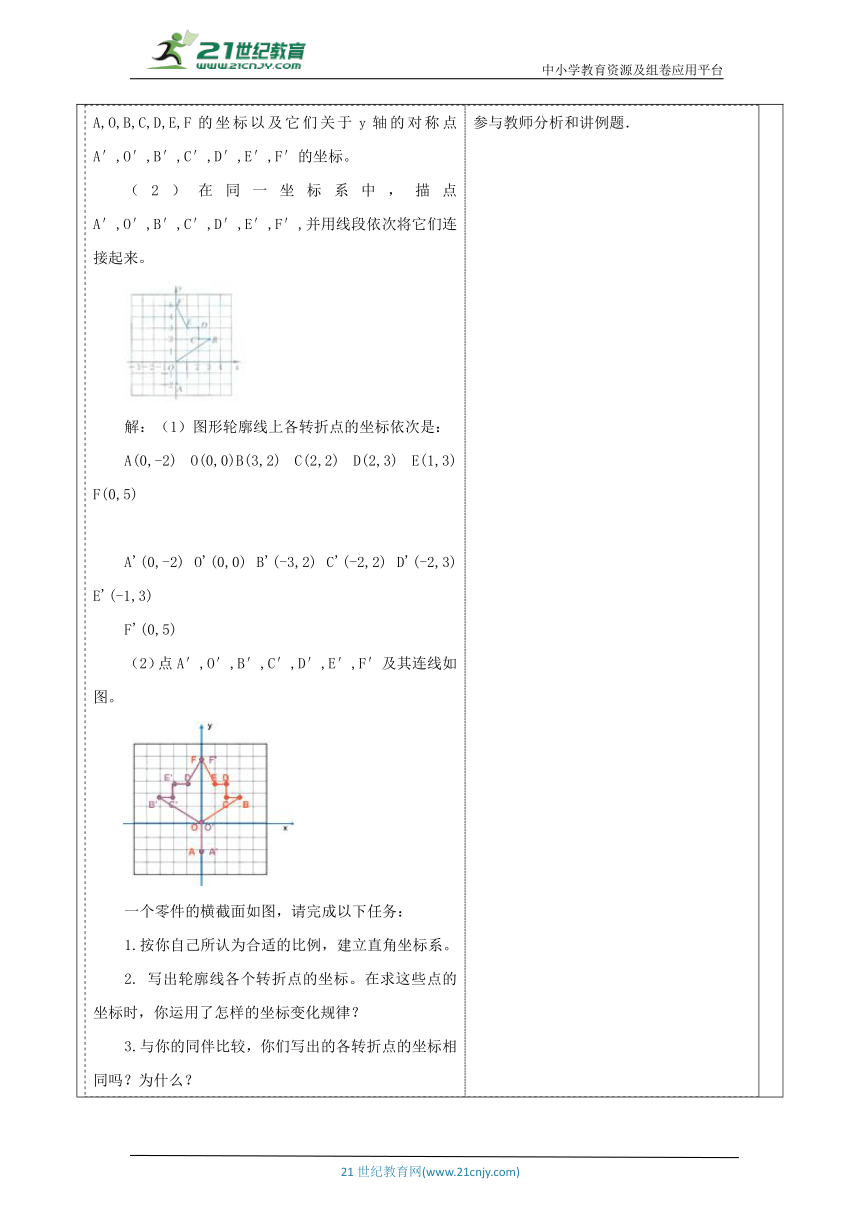
教师活动学生活动环节一:引入新课 1.什么叫轴对称图形? 沿着某一直线对折,直线两旁的部分能够完全重合的图形就是轴对称图形;这条直线称为对称轴. 如何在平面直角坐标系中确定点P的位置? 思考:运用直角坐标系,可以方便地帮助我们表达和处理有关图形的轴对称和平移的问题.先一起看下面的问题: (1)写出点A的坐标. (2)分别作点A关于x轴,y轴的对称点,并写出它们的坐标. 怎样找点A关于x轴的对称点? 怎样找点A关于y轴的对称点? 学生活动1: 学生在教师的引导下,能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明:利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形.使学生亲自经历获取知识的过程,能提高对数学结论的认可程度.环节二:新知探究教师活动2: 合作探究 (3)比较点A与它关于x轴的对称点的坐标,你发现什么规律 横坐标不变,纵坐标互为相反数 (4)比较点A与它关于y轴的对称点的坐标,你发现什么规律 纵坐标不变,横坐标互为相反数 一般规律:在直角坐标系中,点(a,b)关于x轴的对称点的坐标为(a,-b),关于 y轴的对称点的坐标为( - a,b). 学生活动2: 学生自学、互动。在具体计算时,可以通过小组合作交流,放手让学生去思考、讨论,猜想、发现结论. 学生自主解答,教师适时的进行提示 学生思考 活动意图说明:通过数形结合,清晰且直观地认识平面直角坐标系,掌握关于坐标轴对称的两个点的坐标的特点. 环节三:典例精析 例1 (1)求出图形轮廓线上各转折点A,O,B,C,D,E,F的坐标以及它们关于y轴的对称点A′,O′,B′,C′,D′,E′,F′的坐标。 (2)在同一坐标系中,描点A′,O′,B′,C′,D′,E′,F′,并用线段依次将它们连接起来。 解:(1)图形轮廓线上各转折点的坐标依次是: A(0,-2) O(0,0)B(3,2) C(2,2) D(2,3) E(1,3) F(0,5) A'(0,-2) O'(0,0) B'(-3,2) C'(-2,2) D'(-2,3) E'(-1,3) F'(0,5) (2)点A′,O′,B′,C′,D′,E′,F′及其连线如图。 一个零件的横截面如图,请完成以下任务: 1.按你自己所认为合适的比例,建立直角坐标系。 2. 写出轮廓线各个转折点的坐标。在求这些点的坐标时,你运用了怎样的坐标变化规律? 3.与你的同伴比较,你们写出的各转折点的坐标相同吗?为什么? (1)比例尺为1:10 图上尺寸如右图所示 (2)比例尺为1:10,单位:cm 运用了点关于x轴对称,纵坐标不变,横坐标互为相反数的坐标变换规律 (3)因为选定的坐标系不同,所以每个人写出的点的坐标是不一样的 学生活动3: 参与教师分析和讲例题. 活动意图说明: 利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形,通过自主探究增强巩固知识并提高知识认同度.通过动手画图探究坐标轴对称的两个点的坐标关系,使学生获得作轴对称图形的数学活动经验.
板书设计
课堂练习 【知识技能类作业】 必做题: 1.在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是( ) A.(-2,1) B.(-2,-1) C.(-1,2) D.(-1,-2) 2.已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m=______,n= ________. 选做题: 3.如图,△ABC以x轴和y轴为对称轴经过两次轴对称变化后,得到△DEF,如果点A,B,C各点的坐标分别为A(-5,1),B(-2,0),C(1,3),那么D,E,F各点的坐标分别为D__________,E__________,F____________. 【综合拓展类作业】 4. 如图,在直角坐标系中,已知△ABC的顶点坐标分别是A(-2,1),B(1.5,-4),和C(0,3). (1) 分别写出△ABC关于y轴成轴对称的△A′B′C′的顶点坐标;(2) 分别写出△ABC关于x轴成轴对称的△A′′B′′C′′的顶点坐标;(3) 分别画出△A′B′C′与△A′′B′′C′′.
课堂总结
作业设计 【知识技能类作业】 必做题: 1.把△ABC各顶点的横坐标都乘-1,纵坐标不变,所得图形是下列选项中的( ) 选做题: 2.已知点M(2a-b,5+a),N(2b-1,-a+b). (1)若M,N关于x轴对称,试求a,b的值; (2)若M,N关于y轴对称,试求(b+2a)2 015的值. 【综合拓展类作业】 3.如图. (1)写出△ABO各顶点的坐标,以及它们关于y轴的对称点的坐标,并描点 (2)以y轴为对称轴,作△ABO的轴对称图形,然后将所得的图形连同原图形,以x轴为对称轴再作轴对称图形.
教学反思 这节课我们学习了: 一、掌握二种变换: A(a,b) 关于x轴 A1(a,-b) A(a,b) 关于y轴 A2(-a,b) 二、感受一种画法: 学会用简单方法把一个轴对称图形画在直角坐标系中 三、体验一种精神: 学会用数形结合的思想思考问题
21世纪教育网(www.21cnjy.com)
分课时教学设计
第4课时《4.3.1 坐标平面内图形的轴对称和平移》教学设计
课型 新授课√ 复习课口 试卷讲评课口 其他课口
教学内容分析 本节课的主要内容是让学生共同探究,动手操作,通过作图感受坐标平面内图形变化相应的坐标变化,要求学生利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形.本节课内容是在学生学习了轴对称及平面坐标直角系之后进行学习的,为学生探究坐标平面内图形的轴对称奠定了基础。为后续学习图形的变化打好基础,在教材中有着非常重要的地位和作用.
学习者分析 学生具有一定的数形结合意识,且经过一年的初中学习,学生已经具备了初步的逻辑推理能力、空间学习能力及自主学习能力,教师可以多为学生创造自主学习、共同探究的机会,通过动手画图探究坐标轴对称的两个点的坐标关系,使学生获得作轴对称图形的数学活动经验.
教学目标 掌握关于坐标轴对称的两个点的坐标的特点; 2.能在坐标系中作轴对称图形.
教学重点 关于坐标轴对称的两个点之间的坐标关系.
教学难点 利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形的过程比较复杂,是本节教学的难点.
学习活动设计
教师活动学生活动环节一:引入新课 1.什么叫轴对称图形? 沿着某一直线对折,直线两旁的部分能够完全重合的图形就是轴对称图形;这条直线称为对称轴. 如何在平面直角坐标系中确定点P的位置? 思考:运用直角坐标系,可以方便地帮助我们表达和处理有关图形的轴对称和平移的问题.先一起看下面的问题: (1)写出点A的坐标. (2)分别作点A关于x轴,y轴的对称点,并写出它们的坐标. 怎样找点A关于x轴的对称点? 怎样找点A关于y轴的对称点? 学生活动1: 学生在教师的引导下,能很快回忆相关问题. ? 带着问题参与新课. 活动意图说明:利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形.使学生亲自经历获取知识的过程,能提高对数学结论的认可程度.环节二:新知探究教师活动2: 合作探究 (3)比较点A与它关于x轴的对称点的坐标,你发现什么规律 横坐标不变,纵坐标互为相反数 (4)比较点A与它关于y轴的对称点的坐标,你发现什么规律 纵坐标不变,横坐标互为相反数 一般规律:在直角坐标系中,点(a,b)关于x轴的对称点的坐标为(a,-b),关于 y轴的对称点的坐标为( - a,b). 学生活动2: 学生自学、互动。在具体计算时,可以通过小组合作交流,放手让学生去思考、讨论,猜想、发现结论. 学生自主解答,教师适时的进行提示 学生思考 活动意图说明:通过数形结合,清晰且直观地认识平面直角坐标系,掌握关于坐标轴对称的两个点的坐标的特点. 环节三:典例精析 例1 (1)求出图形轮廓线上各转折点A,O,B,C,D,E,F的坐标以及它们关于y轴的对称点A′,O′,B′,C′,D′,E′,F′的坐标。 (2)在同一坐标系中,描点A′,O′,B′,C′,D′,E′,F′,并用线段依次将它们连接起来。 解:(1)图形轮廓线上各转折点的坐标依次是: A(0,-2) O(0,0)B(3,2) C(2,2) D(2,3) E(1,3) F(0,5) A'(0,-2) O'(0,0) B'(-3,2) C'(-2,2) D'(-2,3) E'(-1,3) F'(0,5) (2)点A′,O′,B′,C′,D′,E′,F′及其连线如图。 一个零件的横截面如图,请完成以下任务: 1.按你自己所认为合适的比例,建立直角坐标系。 2. 写出轮廓线各个转折点的坐标。在求这些点的坐标时,你运用了怎样的坐标变化规律? 3.与你的同伴比较,你们写出的各转折点的坐标相同吗?为什么? (1)比例尺为1:10 图上尺寸如右图所示 (2)比例尺为1:10,单位:cm 运用了点关于x轴对称,纵坐标不变,横坐标互为相反数的坐标变换规律 (3)因为选定的坐标系不同,所以每个人写出的点的坐标是不一样的 学生活动3: 参与教师分析和讲例题. 活动意图说明: 利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形,通过自主探究增强巩固知识并提高知识认同度.通过动手画图探究坐标轴对称的两个点的坐标关系,使学生获得作轴对称图形的数学活动经验.
板书设计
课堂练习 【知识技能类作业】 必做题: 1.在平面直角坐标系xOy中,点A与点A1关于x轴对称,点A与点A2关于y轴对称.已知点A1(1,2),则点A2的坐标是( ) A.(-2,1) B.(-2,-1) C.(-1,2) D.(-1,-2) 2.已知点A(m-1,3)与点B(2,n+1)关于x轴对称,则m=______,n= ________. 选做题: 3.如图,△ABC以x轴和y轴为对称轴经过两次轴对称变化后,得到△DEF,如果点A,B,C各点的坐标分别为A(-5,1),B(-2,0),C(1,3),那么D,E,F各点的坐标分别为D__________,E__________,F____________. 【综合拓展类作业】 4. 如图,在直角坐标系中,已知△ABC的顶点坐标分别是A(-2,1),B(1.5,-4),和C(0,3). (1) 分别写出△ABC关于y轴成轴对称的△A′B′C′的顶点坐标;(2) 分别写出△ABC关于x轴成轴对称的△A′′B′′C′′的顶点坐标;(3) 分别画出△A′B′C′与△A′′B′′C′′.
课堂总结
作业设计 【知识技能类作业】 必做题: 1.把△ABC各顶点的横坐标都乘-1,纵坐标不变,所得图形是下列选项中的( ) 选做题: 2.已知点M(2a-b,5+a),N(2b-1,-a+b). (1)若M,N关于x轴对称,试求a,b的值; (2)若M,N关于y轴对称,试求(b+2a)2 015的值. 【综合拓展类作业】 3.如图. (1)写出△ABO各顶点的坐标,以及它们关于y轴的对称点的坐标,并描点 (2)以y轴为对称轴,作△ABO的轴对称图形,然后将所得的图形连同原图形,以x轴为对称轴再作轴对称图形.
教学反思 这节课我们学习了: 一、掌握二种变换: A(a,b) 关于x轴 A1(a,-b) A(a,b) 关于y轴 A2(-a,b) 二、感受一种画法: 学会用简单方法把一个轴对称图形画在直角坐标系中 三、体验一种精神: 学会用数形结合的思想思考问题
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
