5.3一次函数的意义（1） 课件（共26张PPT）

(共26张PPT)
浙教版八年级上册
5.3 一次函数的意义（1）
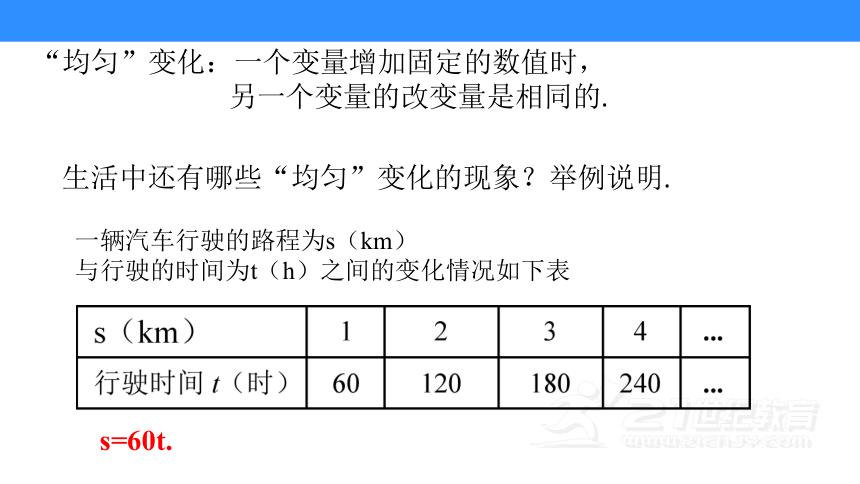
1：驱蚊线香燃烧时间的测量与建模
实验操作：点燃一根驱蚊线香，
每隔1分钟测量一次香可燃烧部分的长度，记录数据.并思考以下问题：
（1）随着时间的增加，香可燃烧部分的长度变化是否均匀，
如果变化是均匀的，燃烧时间每增加1min,香可燃烧部分的长度就减少多少cm
香可燃烧部分的长度变化是均匀的，
燃烧时间每增加1min，香可燃烧部分的长度就减少0.5cm.
(2)估计燃烧10min后香可燃烧的部分的长度，并说明理由.
因为燃烧时间每增加1min，香可燃烧部分的长度就减少0.5cm.
燃烧10min后，香可燃烧的部分的长度为20.4- 5×0.5=17.9cm.
或22.4- 9×0.5=17.9cm.
（3）试写出香可燃烧部分的长度l与燃烧时间t的关系式.
L = -0.5t + 22.9.
L = 22.4-0.5（t -1）
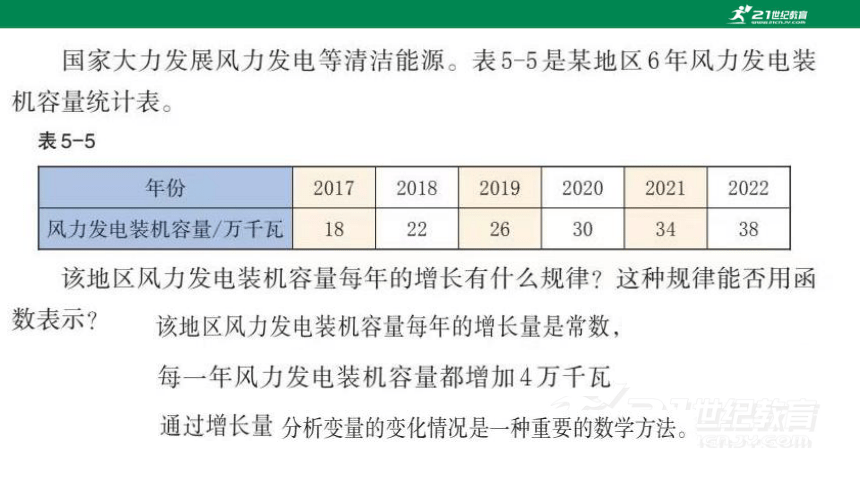
“均匀”变化：一个变量增加固定的数值时，
另一个变量的改变量是相同的.
生活中还有哪些“均匀”变化的现象？举例说明.
一辆汽车行驶的路程为s（km）
与行驶的时间为t（h）之间的变化情况如下表
s=60t.
探究生活中的均匀变化现象中的变化规律
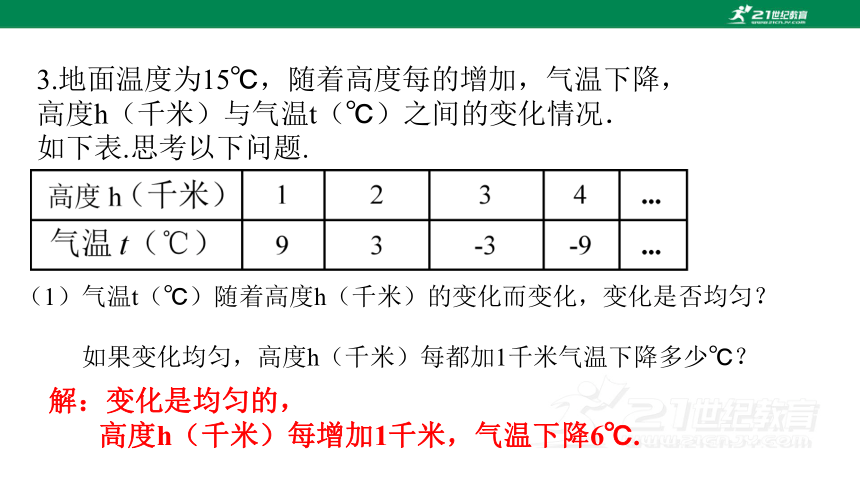
3.地面温度为15℃，随着高度每的增加，气温下降，
高度h（千米）与气温t（℃）之间的变化情况．
如下表.思考以下问题.
（1）气温t（℃）随着高度h（千米）的变化而变化，变化是否均匀？
如果变化均匀，高度h（千米）每都加1千米气温下降多少℃？
解：变化是均匀的，
高度h（千米）每增加1千米，气温下降6℃.
（2）高度为6千米时，气温为多℃？
解：高度为6千米时，气温为-21℃.
（3）试写出高度h（千米）与气温t（℃）之间的关系式.
h=15-6t.
解：h=9-6（t-1）
一般地，形如y=kx+b （k， b 是常数，k≠0）的函数，叫做一次函数.
y=4x+14
一次函数的特点如下：
（1）解析式中自变量x的次数是 次;
（2）比例系数 ；
1
k≠0
L = -0.5t + 22.9.
h=-6t+15.
（3）常数 可以是任意实数.
（4）当 时,一次函数 就成为 （ 为常数, ）,叫做正比例函数,
4.画图直观表示一次函数与正比例函数的关系
写几个一次函数和正比例函数
下列函数中，哪些是一次函数？哪些是正比例函数？系数k和常数项b的值各是多少？
函数 一次函数 正比例函数 系数k 常数项b
C=2πr
y=2(3-x)
s=x(50-x)
是
是
是
不是
不是
不是
是
不是
不是
不是
2π
0
2/3
200
-2
6
例1 求下列各题中x与y之间的关系式，并判断y是否为x的一次函数，是否为正比例函数.
（1）某农场种植玉米，每平方米种玉米6株，玉米株数y与种植面积x（m2）之间的关系.
总株数=每平米株数×面积
y=6x
是一次函数，也是正比例函数.
（2）正方形的面积y与周长x之间的关系.
面积=边长2
周长=4×边长
不是一次函数，也不是正比例函数.
y=
()2
（3）等腰三角形ABC的周长为16（cm），底边BC长为
y（cm），腰AB长为x（cm），y与x之间的关系.
A
B
C
2x＋y＝30
即y＝－2x＋30
是一次函数，不是正比例函数.
y＝30－2x
找到等量关系，确定函数解析式.
例2 按国家2019年1月1日起实施的有关个人所得税的规定，个人取得工资（薪金）中，年应纳税所得额不超过36000元的税率为3%，超过36000元至144000元的部分的税率为10%.
36000
144000
税率为3%
税率为10%
如果小明妈妈的年应纳税所得额是30000元，那么她需要交纳多少税呢？
年应纳税所得额（元）
0
运用图示法，
数形结合更直观
如果年应纳税所得额是50000元，需要交纳多少税呢？
30000×3%=900元
36000×3%＋14000×10%=2480元
（1）设全年应纳税所得额为x元，且36000＜x≤144000，应纳个人所得税为y元，求y关于x的函数表达式和自变量的取值范围.
36000
144000
税率为3%
税率为10%
年应纳税所得额（元）
0
36000×3%
（x-36000）×10%
y＝
＋
＝0.1x－2520
（36000＜x≤144000）
x
（2）小聪妈妈去年应纳税所得额为60000元，则她去年应缴个人所得税多少元？
y＝0.1x－2520（36000＜x≤144000）
解 将x＝60000代入函数表达式，
y＝0.1×60000－2520
＝3480（元）
答：小聪妈妈去年应缴个人所得税3480元.
函数y=kx+b（k,b都是常数，且k≠0）叫做一次函数。
当b=0,一次函数y=kx+b就成为y=kx（k为常数，k≠0），叫做正比例函数，k叫做比例系数。
一次函数
正比例函数
为什么一次函数中k≠0？
因为k=0时,y=0·x+b =b,
即y=b，是一个常量了。
知识小结：
1.写出下列各题中x与y之间的函数关系式，
并判断y是否为x的一次函数 是否为正比例函数
(1)汽车以60千米/时的速度匀速行驶，行驶路程y(千米)与行驶时间x(时)之间的关系.
(2)圆的面积y(厘米2)与它的半径x(厘米)之间的关系；
解：y=60x，y是x的一次函数，也是正比例函数
解： ，y不是x的一次函数，也不是正比例函数
(3)一棵树现在高50厘米，每个月长高2厘米，x月后的高度为y厘米.
解：y=50+2x，y是x的一次函数，但不是x的正比例函数．
夯实基础，稳扎稳打
2.某种气体在0℃时的体积为100L，温度每升高1℃，它的体积增加0.37L.
（1）写出气体体积V(L)与温度t(℃)之间的函数表达式.
（2）求当温度为30℃时气体的体积.
（3）当气体的体积为107.4L时，温度为多少℃？
解 （1）V=100+0.37t (t≥0).
（2）当t=30时，V=111.1(L).
（3）当V=107.4L时，t=20(℃).
解：设y=kx
把x=-2，y=8代入y=kx
∴ -2k=8，∴k=-4
∴y=-4x
当x=3时， y=-4×3=-12
3、已知y是 x的正比例函数，当x=-2时，y=8，
求y关于x的函数表达式，以及当x=3时的函数值
4.已知函数y=（m+1）x+（m2-1）
当m取什么值时，y是x的一次函数？
当m取什么值时，y是x的正比例函数．
解：由函数是一次函数可得，
m+1≠0，解得 m≠-1，
所以，m≠-1时，y是x的一次函数；
函数为正比例函数时，
m+1≠0且m2-1=0，
解得 m=1，
所以，当m=1时，y是x的正比例函数．
5.一种移动通讯服务的收费标准为：每月基本服务费30元，每月免费通话时间为120分，以后每分收费0.4元。
（1）写出每月话费y关于通话时间x(x>120)的函数解析式；
（2）分别求每月通话时间为100分，200分的话费。
（1）y=0.4x-18 (x > 120)
（2）当X=100时,y=30（元），
当x=200时,y=62（元）。
y=180 -
y=90 +
连续递推，豁然开朗
7.某市为了鼓励居民节约用电，采用分段计费的方法按月计算每户家庭的电费．月用电量不超过200度时，按0.55元/度计费；月用电量超过200度时，其中的200度仍按0.55元/度计费，超过部分按0.70元/度计费．设每户家庭月用电量为x度时，应交电费y元．
（1）分别求出0≤x≤200和x＞200时，y与x的函数表达式；
（2）小明家5月份交纳电费117元，小明家这个月用电多少度？
解：（1）当0≤x≤200时，y=0.55x；
当x＞200时，y=0.55×200+0.7（x﹣200），即y=0.7x﹣30。
（2）∵小明家5月份的电费超过110元，
∴把y=117代入y=0.7x﹣30中，得x=210。
答：小明家5月份用电210度。