第四章图形与坐标单元测试卷(含答案)浙教版2025—2026学年八年级上册
文档属性
| 名称 | 第四章图形与坐标单元测试卷(含答案)浙教版2025—2026学年八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 833.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-15 20:50:08 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第四章图形与坐标单元测试卷浙教版2025—2026学年八年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.已知点,则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点在x轴上,点在y轴上,则的值为( )
A.1 B. C.3 D.
3.若点A是平面直角坐标系中第二象限内一点,且点A到x轴的距离为3,到y轴的距离为2,则点A的坐标为( )
A. B. C. D.
4.在平面直角坐标系中,点的坐标分别为,将线段平移得到线段,若点的坐标为,则点的坐标为( )
A. B. C. D.
5.在平面直角坐标系中,第一象限内的点距离轴个单位长度,则的值为( )
A. B.或 C. D.
6.若点在平面直角坐标系中的第二象限,则k的整数值为( )
A. B.0 C.1 D.2
7.在一幅北京旅游景点示意图中,以天安门所在的位置为原点建立平面直角坐标系,记天安门以北约处的国家体育场的坐标为,在天安门以西约处的首钢滑雪大跳台的坐标为,则坐标为的中国人民抗日战争纪念馆相对天安门的位置描述较为准确的是( )
A.在天安门以东约,再往北约处
B.在天安门以西约,再往北约处
C.在天安门以东约,再往南约处
D.在天安门以西约,再往南约处
8.在平面直角坐标系中,点,点,轴,轴,则点的坐标为( )
A. B. C. D.
9.已知点P坐标为,且点P到两坐标轴的距离相等,则点P的坐标是( )
A. B. C.或 D.或
10.现有一点A按照如图所示的指令从原点开始运动,每次运动1个单位长度后就立即改变方向,第一次运动到点,第二次运动到点,…,第次运动到点,则点运动到时点的坐标为( )
A. B. C. D.
二.填空题(每小题5分,满分20分)
11.在平面直角坐标系中,若轴上的点到轴的距离为,则点的坐标是 .
12.在经过某次平移后,顶点的对应点为,若此三角形内任意一点经过此次平移后对应点,则的值为 .
13.平面直角坐标系中有点和点,若线段且与坐标轴平行,则 .
14.如图,在平面直角坐标系中,.点P从点A出发,并按的规律在四边形的边上运动,当点运动的路程为2045时,点所在位置的点的坐标为 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.在平面直角坐标系中,已知点.
(1)当点在轴上时,点的坐标为______;
(2)当直线平行于轴,且,求出点的坐标;
(3)若点到轴、轴的距离相等,求出点的坐标.
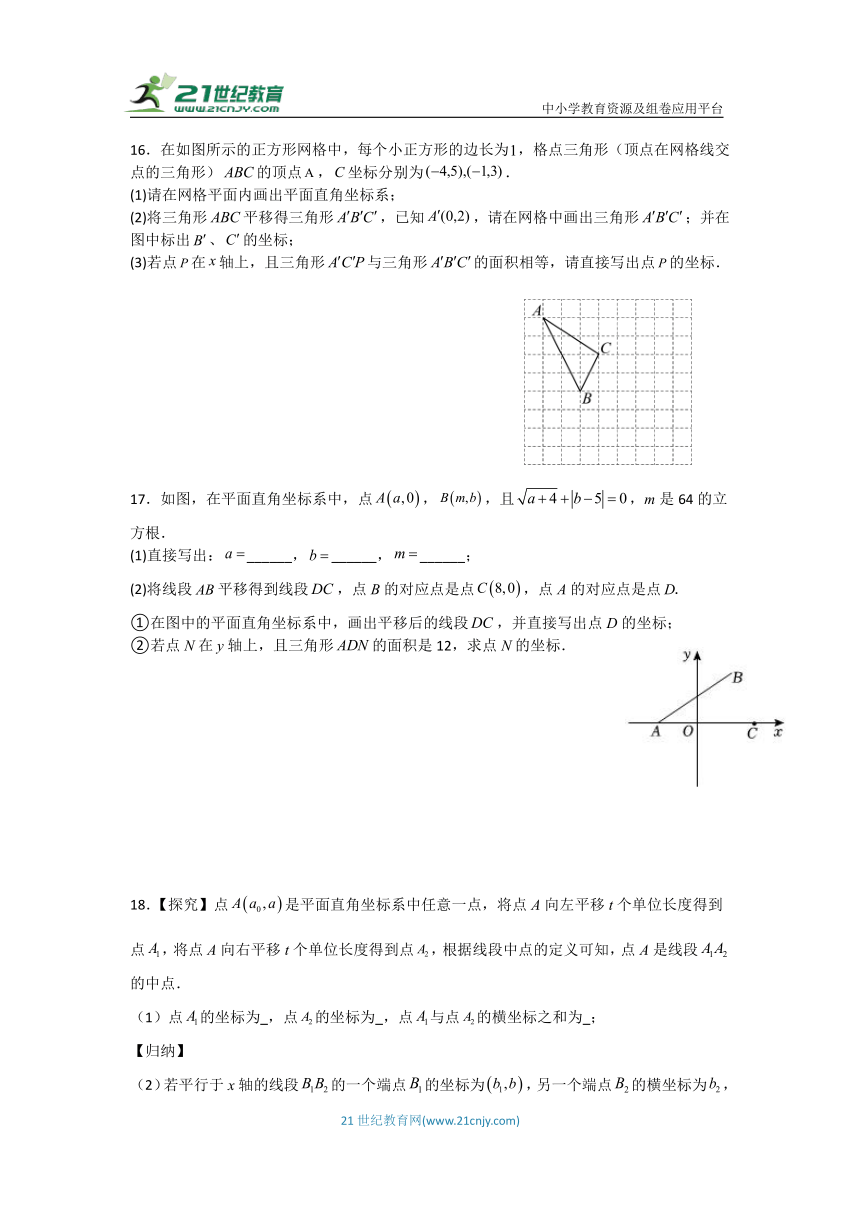
16.在如图所示的正方形网格中,每个小正方形的边长为,格点三角形(顶点在网格线交点的三角形)的顶点,坐标分别为.
(1)请在网格平面内画出平面直角坐标系;
(2)将三角形平移得三角形,已知,请在网格中画出三角形;并在图中标出、的坐标;
(3)若点在轴上,且三角形与三角形的面积相等,请直接写出点的坐标.
17.如图,在平面直角坐标系中,点,,且,m是64的立方根.
(1)直接写出:______,______,______;
(2)将线段平移得到线段,点B的对应点是点,点A的对应点是点
①在图中的平面直角坐标系中,画出平移后的线段,并直接写出点D的坐标;
②若点N在y轴上,且三角形的面积是12,求点N的坐标.
18.【探究】点是平面直角坐标系中任意一点,将点A向左平移t个单位长度得到点,将点A向右平移t个单位长度得到点,根据线段中点的定义可知,点A是线段的中点.
(1)点的坐标为 ,点的坐标为 ,点与点的横坐标之和为 ;
【归纳】
(2)若平行于x轴的线段的一个端点的坐标为,另一个端点的横坐标为,则用含有,和b的式子表示线段的中点坐标为 ;
(3)请利用类似的方法探究并归纳:若平行于y轴的线段的一个端点的坐标为,另一个端点的纵坐标为,则用含有,和c的式子表示线段的中点坐标为 ;
【应用】
(4)已知点M的坐标为,点N的坐标为,点P的坐标为,点Q的坐标为,且线段和线段的中点重合,求m和n的值.
19.已知点,分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到两坐标轴的距离相等;
(4)点P与点的连线平行于x轴.
20.定义:在平面直角坐标系中,对于点,若点坐标为,我们称点是点的等距平移点,其中为等距平移常量.例如:当时,点的等距平移点为.
(1)①当等距平移常量时,点坐标为,则它的等距平移点的坐标为________;
②若点坐标为,它的等距平移点的坐标为,则等距平移常量________.
(2)若点在轴上,且它的等距平移点的坐标为,其中为等距平移常量,为坐标原点,求的面积;
(3)点的等距平移点是,其中为等距平移常量,若,且其中一个点到轴的距离等于另一个点到轴的距离的2倍,求的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B A C D D A C A
二、填空题
11.【解】解:由点在轴上,则纵坐标为,设,
∵点到轴的距离为,
∴,
∴,
∴的坐标为或,
故答案为:或.
12.【解】解:∵在经过此次平移后对应点,
∴的平移规律为:向右平移个单位,向下平移个单位,
∵点经过平移后对应点,
∴,,
∴,,
∴,
即的值为.
故答案为:.
13.【解】解:当轴时,
∵点和点,线段,
∴,
∴或,
∴或;
当轴,
∵点和点,线段,
∴,,
解得:或,
∴或;
综上:或,
故答案为:或.
14.【解】解:,,,,
,,
,
点从点出发,并按的规律在四边形的边上运动,
当点运动的路程为2045时,
,
经历次循环,且走5个单位长度,
点所在位置的点的坐标为,
故答案为:.
三、解答题
15.【解】(1)解:因为点在轴上,
所以,
解得,
则,
所以点坐标为.
故答案为:;
(2)∵直线平行于轴,且,
∴,
解得,
则,
∴点的坐标为;
(3)∵点到轴、轴的距离相等,
则或,
解得或.
当时,
,,
则点坐标为.
当时,
,,
则点坐标为,
综上所述,点的坐标为或.
16.【解】(1)解:建立平面直角坐标系如图所示.
(2)解:∵,
∴三角形向右平移4个单位长度,向下平移3个单位长度得到三角形,
如图,三角形即为所求,,
(3)解:设点P的坐标为,
由题意得,点的坐标为,
∵三角形与三角形的面积相等,
∴,
解得或,
∴点P的坐标为或.
17.【解】(1)解:,
,,
,
是64的立方根,
故答案为:;5;
(2)解:①由得,,,
线段向右平移4个单位长度,向下平移5个单位长度得到线段,
如图,线段即为所求.
点D的坐标为
②设点N的坐标为,
三角形的面积是12,
,
解得或1,
点N的坐标为或
18.【解】解:(1)根据平移可得,点的坐标为,点的坐标为,
点与点的横坐标之和为.
故答案为:;;
(2)由题意可得,,,
∵轴,
∴线段的中点的纵坐标为b,
设点向右平移t个单位长度,点向左平移t个单位长度均得到线段的中点,
∴,
∴,
∴中点的横坐标为,
∴线段的中点的坐标为.
故答案为:
(3)由题意可得,,,
∵轴,
∴线段的中点的横坐标为c,
设点向上平移t个单位长度,点向下平移t个单位长度均得到线段的中点,
∴,
∴,
∴中点的纵坐标为,
∴线段的中点的坐标为.
故答案为:
(4)∵,,
∴线段的中点坐标为,即;
∵,,
∴线段的中点坐标为,即,
∵线段和线段的中点重合,
∴,
解得.
19.【解】(1)解:点P在x轴上,
纵坐标为0,即
,
;
(2)点P在y轴上,
横坐标为0,即,
,
;
(3)点P到两坐标轴的距离相等,
横纵坐标相等或横纵坐标互为相反数
①,即;
;
②,即,
;
综上:或;
(4)点P与点的连线平行于x轴,
点P的纵坐标是3,
即:,
,
.
20.【解】(1)解: ①由定义,N的坐标为:,
故N的坐标为;
故答案为:,
根据定义:,
,解得;
检验:当时,,成立,
故答案为:3.
(2)设M为,根据定义,N的坐标为:,解得,
,
,解得,,
,
的坐标为,
,即N为,
O为原点,
.
(3)N的坐标为,
,
,
,
验证:,符合题意,
其中一个点到轴的距离等于另一个点到轴的距离的2倍,
|或,
因,分情况讨论:
情况一: 即,分四种情况:
①:且(即),
方程变为,解得 ,符合题意;
②:且(即) ,此时,
方程为:解得,,符合题意;
③:且(即) 此时,
方程为:,解得, 不合题意,舍去;
④:且(即且),矛盾,无解;
综上,情况一所有可能的a值为.
情况二: 即|,分四种情况:
①:且(即) ,
方程变为,解得 ,符合题意;
②:且(即) 此时,
方程为:,解得,不合题意,舍去;
③:且(即) 此时,
方程为:,解得, 符合题意;
④:且(矛盾),无解,
综上,情况二解为或.
综上所述,的值为或或或3.
21世纪教育网(www.21cnjy.com)
第四章图形与坐标单元测试卷浙教版2025—2026学年八年级上册
总分:120分 时间:90分钟
姓名:________ 班级:_____________成绩:___________
一.单项选择题(每小题4分,满分40分)
题号 1 3 4 5 6 7 8 9 10
答案
1.已知点,则点P在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在平面直角坐标系中,点在x轴上,点在y轴上,则的值为( )
A.1 B. C.3 D.
3.若点A是平面直角坐标系中第二象限内一点,且点A到x轴的距离为3,到y轴的距离为2,则点A的坐标为( )
A. B. C. D.
4.在平面直角坐标系中,点的坐标分别为,将线段平移得到线段,若点的坐标为,则点的坐标为( )
A. B. C. D.
5.在平面直角坐标系中,第一象限内的点距离轴个单位长度,则的值为( )
A. B.或 C. D.
6.若点在平面直角坐标系中的第二象限,则k的整数值为( )
A. B.0 C.1 D.2
7.在一幅北京旅游景点示意图中,以天安门所在的位置为原点建立平面直角坐标系,记天安门以北约处的国家体育场的坐标为,在天安门以西约处的首钢滑雪大跳台的坐标为,则坐标为的中国人民抗日战争纪念馆相对天安门的位置描述较为准确的是( )
A.在天安门以东约,再往北约处
B.在天安门以西约,再往北约处
C.在天安门以东约,再往南约处
D.在天安门以西约,再往南约处
8.在平面直角坐标系中,点,点,轴,轴,则点的坐标为( )
A. B. C. D.
9.已知点P坐标为,且点P到两坐标轴的距离相等,则点P的坐标是( )
A. B. C.或 D.或
10.现有一点A按照如图所示的指令从原点开始运动,每次运动1个单位长度后就立即改变方向,第一次运动到点,第二次运动到点,…,第次运动到点,则点运动到时点的坐标为( )
A. B. C. D.
二.填空题(每小题5分,满分20分)
11.在平面直角坐标系中,若轴上的点到轴的距离为,则点的坐标是 .
12.在经过某次平移后,顶点的对应点为,若此三角形内任意一点经过此次平移后对应点,则的值为 .
13.平面直角坐标系中有点和点,若线段且与坐标轴平行,则 .
14.如图,在平面直角坐标系中,.点P从点A出发,并按的规律在四边形的边上运动,当点运动的路程为2045时,点所在位置的点的坐标为 .
三.解答题(共6小题,总分60分,每题须有必要的文字说明和解答过程)
15.在平面直角坐标系中,已知点.
(1)当点在轴上时,点的坐标为______;
(2)当直线平行于轴,且,求出点的坐标;
(3)若点到轴、轴的距离相等,求出点的坐标.
16.在如图所示的正方形网格中,每个小正方形的边长为,格点三角形(顶点在网格线交点的三角形)的顶点,坐标分别为.
(1)请在网格平面内画出平面直角坐标系;
(2)将三角形平移得三角形,已知,请在网格中画出三角形;并在图中标出、的坐标;
(3)若点在轴上,且三角形与三角形的面积相等,请直接写出点的坐标.
17.如图,在平面直角坐标系中,点,,且,m是64的立方根.
(1)直接写出:______,______,______;
(2)将线段平移得到线段,点B的对应点是点,点A的对应点是点
①在图中的平面直角坐标系中,画出平移后的线段,并直接写出点D的坐标;
②若点N在y轴上,且三角形的面积是12,求点N的坐标.
18.【探究】点是平面直角坐标系中任意一点,将点A向左平移t个单位长度得到点,将点A向右平移t个单位长度得到点,根据线段中点的定义可知,点A是线段的中点.
(1)点的坐标为 ,点的坐标为 ,点与点的横坐标之和为 ;
【归纳】
(2)若平行于x轴的线段的一个端点的坐标为,另一个端点的横坐标为,则用含有,和b的式子表示线段的中点坐标为 ;
(3)请利用类似的方法探究并归纳:若平行于y轴的线段的一个端点的坐标为,另一个端点的纵坐标为,则用含有,和c的式子表示线段的中点坐标为 ;
【应用】
(4)已知点M的坐标为,点N的坐标为,点P的坐标为,点Q的坐标为,且线段和线段的中点重合,求m和n的值.
19.已知点,分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到两坐标轴的距离相等;
(4)点P与点的连线平行于x轴.
20.定义:在平面直角坐标系中,对于点,若点坐标为,我们称点是点的等距平移点,其中为等距平移常量.例如:当时,点的等距平移点为.
(1)①当等距平移常量时,点坐标为,则它的等距平移点的坐标为________;
②若点坐标为,它的等距平移点的坐标为,则等距平移常量________.
(2)若点在轴上,且它的等距平移点的坐标为,其中为等距平移常量,为坐标原点,求的面积;
(3)点的等距平移点是,其中为等距平移常量,若,且其中一个点到轴的距离等于另一个点到轴的距离的2倍,求的值.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B A C D D A C A
二、填空题
11.【解】解:由点在轴上,则纵坐标为,设,
∵点到轴的距离为,
∴,
∴,
∴的坐标为或,
故答案为:或.
12.【解】解:∵在经过此次平移后对应点,
∴的平移规律为:向右平移个单位,向下平移个单位,
∵点经过平移后对应点,
∴,,
∴,,
∴,
即的值为.
故答案为:.
13.【解】解:当轴时,
∵点和点,线段,
∴,
∴或,
∴或;
当轴,
∵点和点,线段,
∴,,
解得:或,
∴或;
综上:或,
故答案为:或.
14.【解】解:,,,,
,,
,
点从点出发,并按的规律在四边形的边上运动,
当点运动的路程为2045时,
,
经历次循环,且走5个单位长度,
点所在位置的点的坐标为,
故答案为:.
三、解答题
15.【解】(1)解:因为点在轴上,
所以,
解得,
则,
所以点坐标为.
故答案为:;
(2)∵直线平行于轴,且,
∴,
解得,
则,
∴点的坐标为;
(3)∵点到轴、轴的距离相等,
则或,
解得或.
当时,
,,
则点坐标为.
当时,
,,
则点坐标为,
综上所述,点的坐标为或.
16.【解】(1)解:建立平面直角坐标系如图所示.
(2)解:∵,
∴三角形向右平移4个单位长度,向下平移3个单位长度得到三角形,
如图,三角形即为所求,,
(3)解:设点P的坐标为,
由题意得,点的坐标为,
∵三角形与三角形的面积相等,
∴,
解得或,
∴点P的坐标为或.
17.【解】(1)解:,
,,
,
是64的立方根,
故答案为:;5;
(2)解:①由得,,,
线段向右平移4个单位长度,向下平移5个单位长度得到线段,
如图,线段即为所求.
点D的坐标为
②设点N的坐标为,
三角形的面积是12,
,
解得或1,
点N的坐标为或
18.【解】解:(1)根据平移可得,点的坐标为,点的坐标为,
点与点的横坐标之和为.
故答案为:;;
(2)由题意可得,,,
∵轴,
∴线段的中点的纵坐标为b,
设点向右平移t个单位长度,点向左平移t个单位长度均得到线段的中点,
∴,
∴,
∴中点的横坐标为,
∴线段的中点的坐标为.
故答案为:
(3)由题意可得,,,
∵轴,
∴线段的中点的横坐标为c,
设点向上平移t个单位长度,点向下平移t个单位长度均得到线段的中点,
∴,
∴,
∴中点的纵坐标为,
∴线段的中点的坐标为.
故答案为:
(4)∵,,
∴线段的中点坐标为,即;
∵,,
∴线段的中点坐标为,即,
∵线段和线段的中点重合,
∴,
解得.
19.【解】(1)解:点P在x轴上,
纵坐标为0,即
,
;
(2)点P在y轴上,
横坐标为0,即,
,
;
(3)点P到两坐标轴的距离相等,
横纵坐标相等或横纵坐标互为相反数
①,即;
;
②,即,
;
综上:或;
(4)点P与点的连线平行于x轴,
点P的纵坐标是3,
即:,
,
.
20.【解】(1)解: ①由定义,N的坐标为:,
故N的坐标为;
故答案为:,
根据定义:,
,解得;
检验:当时,,成立,
故答案为:3.
(2)设M为,根据定义,N的坐标为:,解得,
,
,解得,,
,
的坐标为,
,即N为,
O为原点,
.
(3)N的坐标为,
,
,
,
验证:,符合题意,
其中一个点到轴的距离等于另一个点到轴的距离的2倍,
|或,
因,分情况讨论:
情况一: 即,分四种情况:
①:且(即),
方程变为,解得 ,符合题意;
②:且(即) ,此时,
方程为:解得,,符合题意;
③:且(即) 此时,
方程为:,解得, 不合题意,舍去;
④:且(即且),矛盾,无解;
综上,情况一所有可能的a值为.
情况二: 即|,分四种情况:
①:且(即) ,
方程变为,解得 ,符合题意;
②:且(即) 此时,
方程为:,解得,不合题意,舍去;
③:且(即) 此时,
方程为:,解得, 符合题意;
④:且(矛盾),无解,
综上,情况二解为或.
综上所述,的值为或或或3.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
