5.2.1 认识函数 课件(共27张PPT)
文档属性
| 名称 | 5.2.1 认识函数 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-10-20 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
第二章 特殊三角形
5.2.1 认识函数
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.了解函数的概念和三种表示方法;
2.了解函数值的概念,并会求一个数的函数值.
02
新知导入
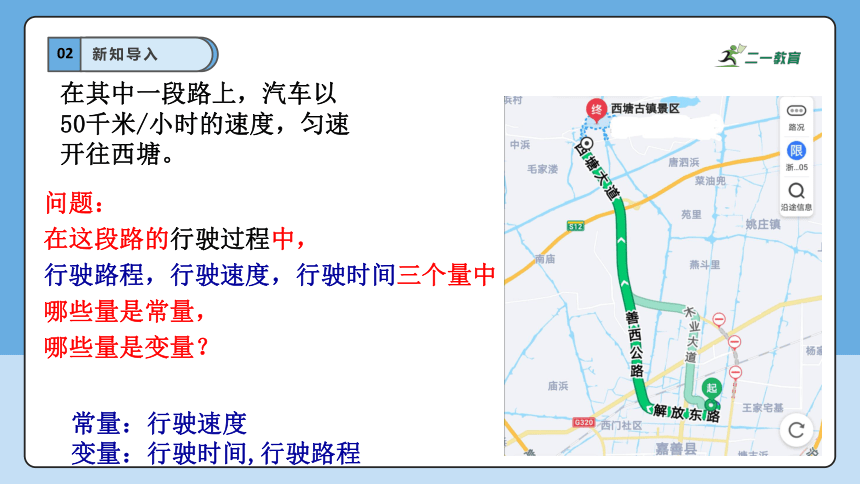
在其中一段路上,汽车以
50千米/小时的速度,匀速
开往西塘。
问题:
在这段路的行驶过程中,
行驶路程,行驶速度,行驶时间三个量中
哪些量是常量,
哪些量是变量?
常量:行驶速度
变量:行驶时间,行驶路程
03
新知探究
合作学习
问题1 小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按20元/时计算.设小明的哥哥这个月工作的时间为t时,应得报酬为m元,填写下表:
然后回答下列问题:
工作时间t (时)
6
8
12
16
24
…
…
报酬m (元))
…
…
…
(1)在上述问题中,哪些是常量?哪些是变量?
(2)表中m的值是否随t的变化而变化?
(3)怎样用关于t的代数式表示m
t
03
新知探究
03
新知讲解
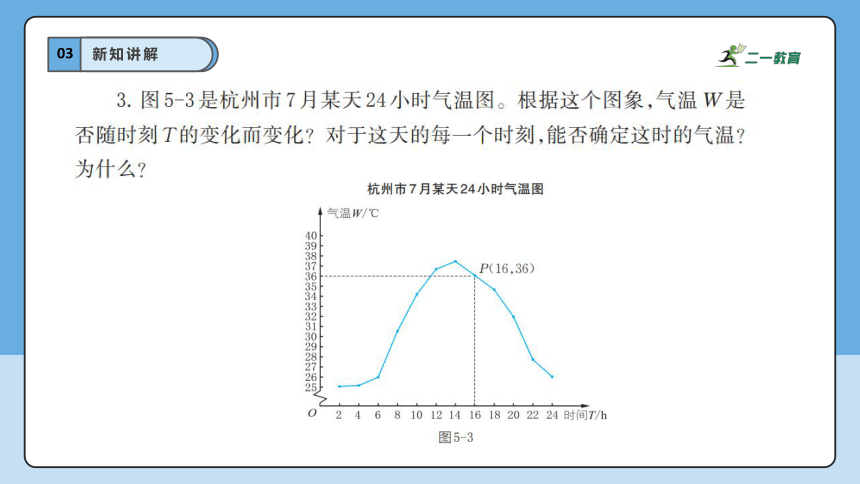
03
新知讲解
提炼概念
一般地,在一个变化过程中的两个变量 和 ,
如果对于 的每一个值, 都有唯一的值与它对应, 那么我们称 是 的函数(function), 叫做自变量.
①有两个变量
②一个变量每确定一个值,另一个变量有唯一的值与它对应
判断是否存在函数关系的两个关键点:
y随着x的确定而唯一确定
引发变化过程的变量
03
新知讲解
是
不是
03
新知讲解
03
新知讲解
新课探究
例
03
新知讲解
03
新知讲解
归纳概念
【总结归纳】函数的三种表示方法
(1)图象法(用图象来表示函数的方法);
(2)列表法(把自变量x的一系列值和函数y的对应值列成一个表格来表示函数的方法);
(3)解析式法(用代数式来表示函数的方法,用来表示函数关系的式子叫做函数关系式,函数关系式是等式,在书写时有顺序性,一般写成:“函数=函数自变量的代数式”的形式).
04
课堂练习
【知识技能类作业】必做题:
1.下列各曲线中不能表示y是x的函数的是 ( )
A. B.
C. D.
D
04
课堂练习
【知识技能类作业】必做题:
2.有下列关于变量x和y的关系:
①3x-2y=5; ②y= |x|; ③y2=x ;
其中表示y是x的函数关系的是________
① ②
y是x的函数要求一个x值只能对应一个y值,但一个y值可以对应数个x值
①可以写成y=1.5x-2.5,一次函数成立
②中一个x值对应的y只有一个,成立
③中一个x有两个y值可与之对应,所以不是满足条件
04
课堂练习
【知识技能类作业】选做题:
3.观察下列各图,每条边上有n(n ≥ 2)个圆点,每个图案中的圆点的总数是s
n=2,s=3
n=3,s=6
n=4,s=9
(1)图中s可以看作n的函数吗?
(2)按此规律推出s与n的关系式?
(3)求出当n=100时,s的值。
(1)可以 (2)s=3n-3 (3)297
04
课堂练习
【综合拓展类作业】
4.四川的横断山脉属典型的高山气候,山脚鸟语花香,山顶白雪皑皑,一科研小组想研究气温随山高的变化规律,已知测定地面气温是20 ℃,如果每升高1 km,气温下降6 ℃,请写出气温t(℃)与高度h(km)的函数关系式,并求出高度分别为1 km,5 km,7 km时的气温.
04
课堂练习
【综合拓展类作业】
解: 气温t(℃)与高度h(km)的关系式为
t=20-6h.
当h=1 km时,t=20-6=14(℃);
当h=5 km时,t=20-6×5=-10(℃);
当h=7 km时,t=20-6×7=-22(℃).
综上所述,当高度分别为1 km,5 km,7 km时,
气温分别是14 ℃,-10 ℃,-22 ℃.
05
课堂小结
丰收园
1、一般地,在某个变化过程中,设有两个变量x和y,
如果对于x的________________,y都有____________,
那我们就说___是___的函数,其中x叫做________.
每一个确定的值
唯一确定的值
y
x
自变量
2、函数的三种常用表示方法是___________ , __________ ,__________
解析法
图象法
列表法
3、求函数值常用___________,___________,
___________的办法来求.
代一代
画一画
查一查
06
作业布置
【知识技能类作业】必做题:
1.下列关系中,y不是x的函数的是 ( )
D
06
作业布置
【知识技能类作业】选做题:
课堂练习
2.已知△ABC的底边BC上的高线长是6cm。当BC的长改变时,三角形的面积也将改变.
(1)若△ABC的底边BC的长为x(cm),则△ABC的面积y(cm2)可表示为 .
(2)当底边长从12cm变化到3cm时,三角形的面积从 cm2变化到 cm2.
(1)y=3x (2)36 9
06
作业布置
【知识技能类作业】选做题:
课堂练习
课堂练习
3.一水池内有水90立方米,设全池水排尽的时间为y分
钟,每分钟的排水量为x立方米,排水时间的范围
是9≤y≤15。
(1)求y关于x的函数解析式,并指出每分钟排水量
x的取值范围;
(2)在坐标系中画出此函数的图象;
(3)根据图象求当每分钟排水量为9立方米时,排水需多少分钟?当排水时间为10分钟时,每分钟的排水量是多少立方米?
06
作业布置
【综合拓展类作业】
(3)令x=9,解得y=10,
令y=10求得x=9,
∴当每分钟排水量为9立方米时,排水需10分钟;当排水时间为10分钟时,每分钟的排水量是9立方米.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第二章 特殊三角形
5.2.1 认识函数
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
1.了解函数的概念和三种表示方法;
2.了解函数值的概念,并会求一个数的函数值.
02
新知导入
在其中一段路上,汽车以
50千米/小时的速度,匀速
开往西塘。
问题:
在这段路的行驶过程中,
行驶路程,行驶速度,行驶时间三个量中
哪些量是常量,
哪些量是变量?
常量:行驶速度
变量:行驶时间,行驶路程
03
新知探究
合作学习
问题1 小明的哥哥是一名大学生,他利用暑假去一家公司打工,报酬按20元/时计算.设小明的哥哥这个月工作的时间为t时,应得报酬为m元,填写下表:
然后回答下列问题:
工作时间t (时)
6
8
12
16
24
…
…
报酬m (元))
…
…
…
(1)在上述问题中,哪些是常量?哪些是变量?
(2)表中m的值是否随t的变化而变化?
(3)怎样用关于t的代数式表示m
t
03
新知探究
03
新知讲解
03
新知讲解
提炼概念
一般地,在一个变化过程中的两个变量 和 ,
如果对于 的每一个值, 都有唯一的值与它对应, 那么我们称 是 的函数(function), 叫做自变量.
①有两个变量
②一个变量每确定一个值,另一个变量有唯一的值与它对应
判断是否存在函数关系的两个关键点:
y随着x的确定而唯一确定
引发变化过程的变量
03
新知讲解
是
不是
03
新知讲解
03
新知讲解
新课探究
例
03
新知讲解
03
新知讲解
归纳概念
【总结归纳】函数的三种表示方法
(1)图象法(用图象来表示函数的方法);
(2)列表法(把自变量x的一系列值和函数y的对应值列成一个表格来表示函数的方法);
(3)解析式法(用代数式来表示函数的方法,用来表示函数关系的式子叫做函数关系式,函数关系式是等式,在书写时有顺序性,一般写成:“函数=函数自变量的代数式”的形式).
04
课堂练习
【知识技能类作业】必做题:
1.下列各曲线中不能表示y是x的函数的是 ( )
A. B.
C. D.
D
04
课堂练习
【知识技能类作业】必做题:
2.有下列关于变量x和y的关系:
①3x-2y=5; ②y= |x|; ③y2=x ;
其中表示y是x的函数关系的是________
① ②
y是x的函数要求一个x值只能对应一个y值,但一个y值可以对应数个x值
①可以写成y=1.5x-2.5,一次函数成立
②中一个x值对应的y只有一个,成立
③中一个x有两个y值可与之对应,所以不是满足条件
04
课堂练习
【知识技能类作业】选做题:
3.观察下列各图,每条边上有n(n ≥ 2)个圆点,每个图案中的圆点的总数是s
n=2,s=3
n=3,s=6
n=4,s=9
(1)图中s可以看作n的函数吗?
(2)按此规律推出s与n的关系式?
(3)求出当n=100时,s的值。
(1)可以 (2)s=3n-3 (3)297
04
课堂练习
【综合拓展类作业】
4.四川的横断山脉属典型的高山气候,山脚鸟语花香,山顶白雪皑皑,一科研小组想研究气温随山高的变化规律,已知测定地面气温是20 ℃,如果每升高1 km,气温下降6 ℃,请写出气温t(℃)与高度h(km)的函数关系式,并求出高度分别为1 km,5 km,7 km时的气温.
04
课堂练习
【综合拓展类作业】
解: 气温t(℃)与高度h(km)的关系式为
t=20-6h.
当h=1 km时,t=20-6=14(℃);
当h=5 km时,t=20-6×5=-10(℃);
当h=7 km时,t=20-6×7=-22(℃).
综上所述,当高度分别为1 km,5 km,7 km时,
气温分别是14 ℃,-10 ℃,-22 ℃.
05
课堂小结
丰收园
1、一般地,在某个变化过程中,设有两个变量x和y,
如果对于x的________________,y都有____________,
那我们就说___是___的函数,其中x叫做________.
每一个确定的值
唯一确定的值
y
x
自变量
2、函数的三种常用表示方法是___________ , __________ ,__________
解析法
图象法
列表法
3、求函数值常用___________,___________,
___________的办法来求.
代一代
画一画
查一查
06
作业布置
【知识技能类作业】必做题:
1.下列关系中,y不是x的函数的是 ( )
D
06
作业布置
【知识技能类作业】选做题:
课堂练习
2.已知△ABC的底边BC上的高线长是6cm。当BC的长改变时,三角形的面积也将改变.
(1)若△ABC的底边BC的长为x(cm),则△ABC的面积y(cm2)可表示为 .
(2)当底边长从12cm变化到3cm时,三角形的面积从 cm2变化到 cm2.
(1)y=3x (2)36 9
06
作业布置
【知识技能类作业】选做题:
课堂练习
课堂练习
3.一水池内有水90立方米,设全池水排尽的时间为y分
钟,每分钟的排水量为x立方米,排水时间的范围
是9≤y≤15。
(1)求y关于x的函数解析式,并指出每分钟排水量
x的取值范围;
(2)在坐标系中画出此函数的图象;
(3)根据图象求当每分钟排水量为9立方米时,排水需多少分钟?当排水时间为10分钟时,每分钟的排水量是多少立方米?
06
作业布置
【综合拓展类作业】
(3)令x=9,解得y=10,
令y=10求得x=9,
∴当每分钟排水量为9立方米时,排水需10分钟;当排水时间为10分钟时,每分钟的排水量是9立方米.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
