浙教版八上1.3证明(第1课时) 同步教学课件(25张ppt)
文档属性
| 名称 | 浙教版八上1.3证明(第1课时) 同步教学课件(25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览




文档简介
第1章 三角形的初步认识
1.3证明(第1课时)
(浙教版)八年级
上
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
板书设计
01
教学目标
01
02
知道证明的含义和证明的必要性。
会按规定格式证明简单的命题。
02
新知导入
a
b
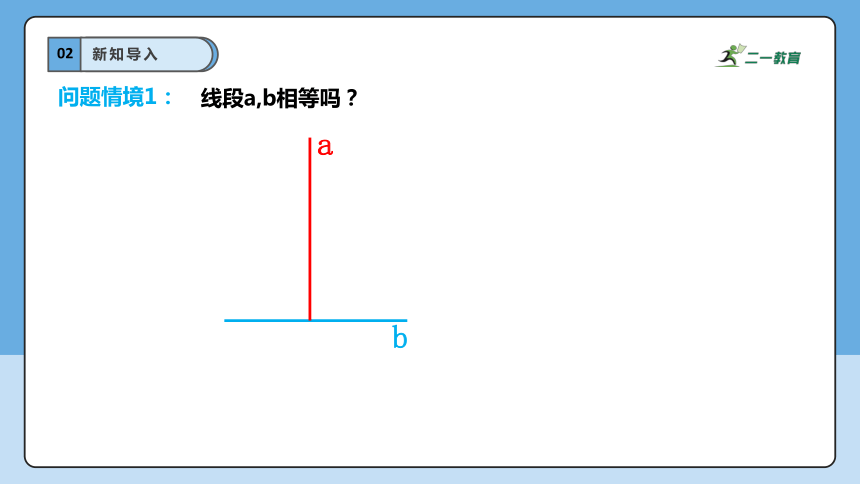
问题情境1:
线段a,b相等吗?
02
新知导入
a
b
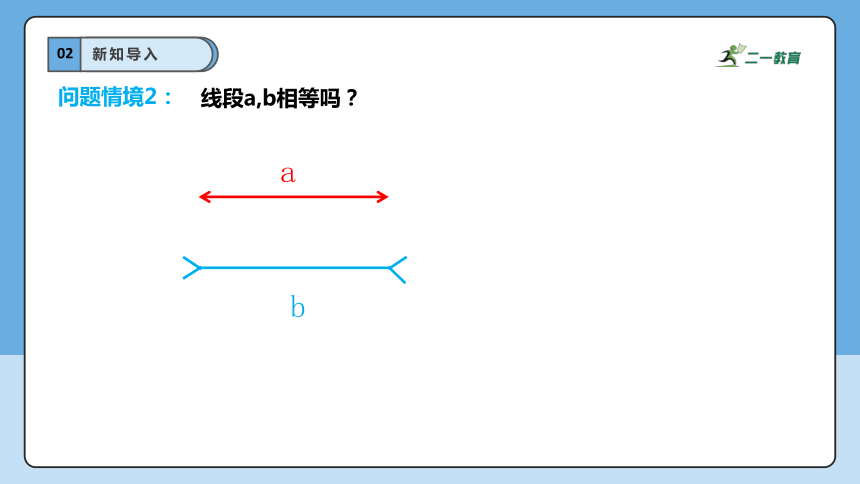
问题情境2:
线段a,b相等吗?
02
新知导入
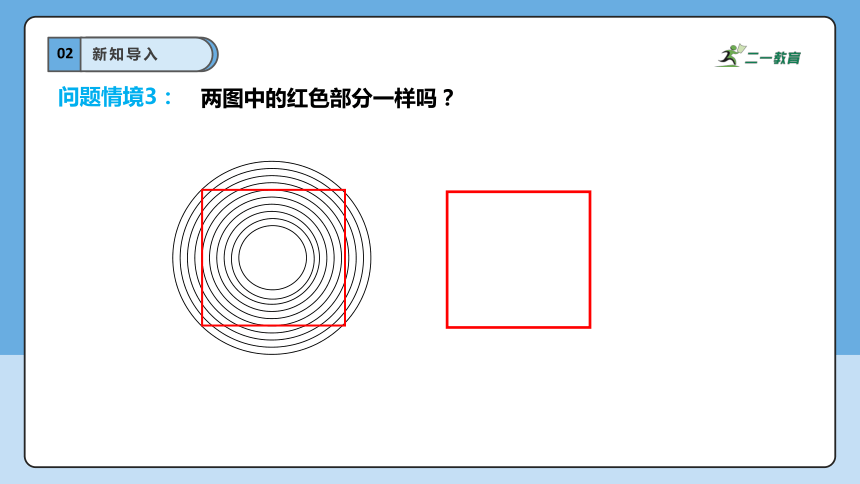
问题情境3:
两图中的红色部分一样吗?
如图,一组直线 a,b,c,d 是否互相平行?
a
b
c
d
问题情境4:
02
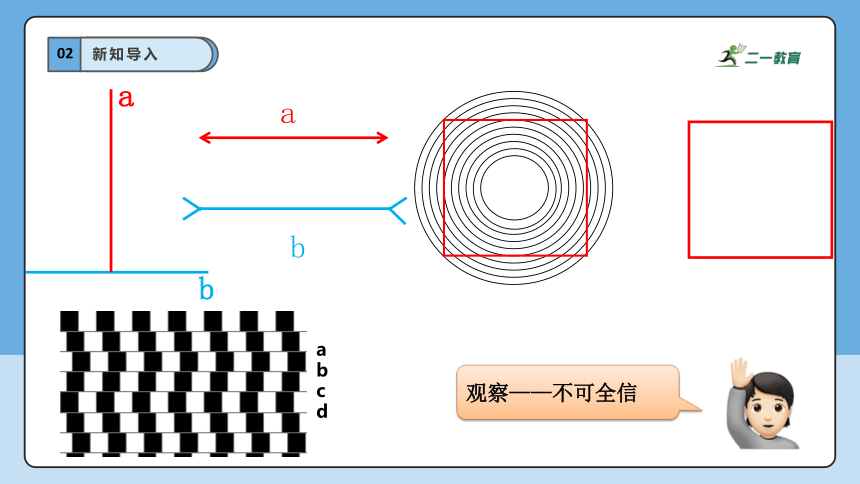
新知导入
观察——不可全信
a
b
c
d
a
b
a
b
02
新知导入
当n=0,1,2,3,4,5时,代数式n2-3n+7 的值分别是 7,5,5,7,11,17,它们都是质数,那么,命题“对于自然数 n,代数式 n2-3n+7的值都是质数”是真命题吗?
列举——不够严谨
当n=6时, n?-3n+7 =25不是质数
问题情境5:
02
新知导入
02
新知导入
哦……那可
怎么办
【思考】如何证实一个命题是真命题?
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的?
能不能根据已经知道的真命题证实呢?
03
新知探究
证明:
要判断一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立。这样的推理过程叫作证明。
证明中的每一步推理都要有根据,不能“想当然”.这些根据,可以是已知条件,也可以是学过的定义、基本事实、定理等.
定理一定是真命题,但真命题不一定是定理.
03
新知探究
证明的格式:
证明的基本格式:因为?? ,所以……。
注意:“因为”后面是已知条件、已证、定义、定理、基本事实
等,“所以”后面是由此推出的结果。
?
03
新知讲解
已知:如图,DE∥BC,∠1=∠E。
求证:BE平分∠ABC。
例1
证明:因为DE∥BC(已知),
所以∠2=∠E(两直线平行,内错角相等)。
又因为∠1=∠E(已知),
所以∠1=∠2,
所以BE平分∠ABC(角平分线的定义)。
03
新知讲解
已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE。
求证:∠PEF+∠PFE=90。
例2
证明:因为EP,FP分别平分∠BEF,∠DFE(已知),
所以∠PEF=????????∠BEF,
∠PFE=????????∠DFE(角平分线的定义)。
因为AB∥CD(已知),
所以∠BEF+∠DFE=180°(两直线平行,同旁内角互补)。
故有∠PEF+∠PFE=????????∠BEF+????????∠DFE=????????(∠BEF+∠DFE)=????????×180°=90°。
?
证明过程中的每一步推理都要有
依据,依据作为推理的理由,可以写在每一步后的括号内。
03
新知讲解
试一试
在下面的括号内,填上推理的根据.
如图,∠A +∠B=180°,求证∠C +∠D=180°.
证明:∵∠A+∠B=180°,
∴AD∥BC(_________________________),
∴∠C+∠D=180°(_________________________).
同旁内角互补,两直线平行
两直线平行,同旁内角互补
04
课堂练习
基础题
1.关于证明,下列说法不正确的是( )
A.证明是说明命题是真命题的过程
B.要判定一个命题是真命题常常通过推理的方式
C.要说明一个命题是假命题常采用举反例的方式
D.真命题与假命题都可以通过举反例来说明
D
04
课堂练习
基础题
2. 如图,下列证明正确的是( C )
A. 因为BC∥AD,所以∠1=∠4
B. 因为∠2=∠3,所以AB∥CD
C. 因为∠C+∠ADC=180°,所以AD∥BC
D. 因为BC∥AD,所以∠ABC+∠C=180°
C
3.有一条直的宽纸带,按如图所示的方式折叠,则∠α的度数等于( )
A.50° B.60°
C.75° D.85°
C
04
课堂练习
基础题
4. 如图,小明观察两个图形后,认为图①中间的圆要比图②中间的圆小,通过测量发现他的判断是? 错误 (填“正确”或“错误”)的,由此可以得出观察? 不能 (填“能”或“不能”)作为证明的依据.
错误
不能
04
课堂练习
基础题
5. 如图,AB∥CD,∠B=∠D,EF与AD交于点E,与BC的延长线交于点F. 求证:∠DEF=∠F.
解:因为AB∥CD(已知),
所以∠DCF=∠B(两直线平行,同位角相等).
因为∠B=∠D(已知),所以∠DCF=∠D(等量代换).
所以AD∥BC(内错角相等,两直线平行).
所以∠DEF=∠F(两直线平行,内错角相等)
04
课堂练习
提升题
1. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( B )
A. ∠α+∠β=180°
B. ∠β-∠α=90°
C. ∠β=3∠α
D. ∠α+∠β=90°
B
2. 如图,若AB∥EF,∠B=40°,则当∠E=? 140° 时,BC∥DE.
140°
04
课堂练习
拓展题
1. 如图,E,F分别为四边形ABDC的边CA的延长线上两点,连结DE,BF,DE交边AB于点G,H为边CD的延长线上一点,作∠BDH的平分线DP,交边AB的延长线于点P,∠1=∠2,∠3=∠4,∠5=∠C.
试判断DE与BF是否平行,并说明理由;
解:DE∥BF 理由:因为∠3=∠4(已知),
所以BD∥CE(内错角相等,两直线平行).
所以∠5=∠BAF(两直线平行,内错角相等).
因为∠5=∠C(已知),所以∠C=∠BAF(等量代换).
所以CD∥AB(同位角相等,两直线平行).
所以∠2=∠BGD(两直线平行,内错角相等).
因为∠1=∠2(已知),所以∠BGD=∠1(等量代换).
所以DE∥BF(内错角相等,两直线平行).
05
课堂小结
1.证明:
要判断一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立。这样的推理过程叫作证明。
2.证明的格式:
证明的基本格式:因为?? ,所以……。
注意:“因为”后面是已知条件、已证、定义、定理、基本事实
等,“所以”后面是由此推出的结果。
?
06
板书设计
1.3证明(第1课时)
1.证明:
2.证明的格式:
Thanks!
https://www.21cnjy.com/recruitment/home/fine
1.3证明(第1课时)
(浙教版)八年级
上
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
板书设计
01
教学目标
01
02
知道证明的含义和证明的必要性。
会按规定格式证明简单的命题。
02
新知导入
a
b
问题情境1:
线段a,b相等吗?
02
新知导入
a
b
问题情境2:
线段a,b相等吗?
02
新知导入
问题情境3:
两图中的红色部分一样吗?
如图,一组直线 a,b,c,d 是否互相平行?
a
b
c
d
问题情境4:
02
新知导入
观察——不可全信
a
b
c
d
a
b
a
b
02
新知导入
当n=0,1,2,3,4,5时,代数式n2-3n+7 的值分别是 7,5,5,7,11,17,它们都是质数,那么,命题“对于自然数 n,代数式 n2-3n+7的值都是质数”是真命题吗?
列举——不够严谨
当n=6时, n?-3n+7 =25不是质数
问题情境5:
02
新知导入
02
新知导入
哦……那可
怎么办
【思考】如何证实一个命题是真命题?
用我们以前学过的观察,实验,验证特例等方法.
这些方法往往并不可靠.
那已经知道的真命题又是如何证实的?
能不能根据已经知道的真命题证实呢?
03
新知探究
证明:
要判断一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立。这样的推理过程叫作证明。
证明中的每一步推理都要有根据,不能“想当然”.这些根据,可以是已知条件,也可以是学过的定义、基本事实、定理等.
定理一定是真命题,但真命题不一定是定理.
03
新知探究
证明的格式:
证明的基本格式:因为?? ,所以……。
注意:“因为”后面是已知条件、已证、定义、定理、基本事实
等,“所以”后面是由此推出的结果。
?
03
新知讲解
已知:如图,DE∥BC,∠1=∠E。
求证:BE平分∠ABC。
例1
证明:因为DE∥BC(已知),
所以∠2=∠E(两直线平行,内错角相等)。
又因为∠1=∠E(已知),
所以∠1=∠2,
所以BE平分∠ABC(角平分线的定义)。
03
新知讲解
已知:如图,AB∥CD,EP,FP分别平分∠BEF,∠DFE。
求证:∠PEF+∠PFE=90。
例2
证明:因为EP,FP分别平分∠BEF,∠DFE(已知),
所以∠PEF=????????∠BEF,
∠PFE=????????∠DFE(角平分线的定义)。
因为AB∥CD(已知),
所以∠BEF+∠DFE=180°(两直线平行,同旁内角互补)。
故有∠PEF+∠PFE=????????∠BEF+????????∠DFE=????????(∠BEF+∠DFE)=????????×180°=90°。
?
证明过程中的每一步推理都要有
依据,依据作为推理的理由,可以写在每一步后的括号内。
03
新知讲解
试一试
在下面的括号内,填上推理的根据.
如图,∠A +∠B=180°,求证∠C +∠D=180°.
证明:∵∠A+∠B=180°,
∴AD∥BC(_________________________),
∴∠C+∠D=180°(_________________________).
同旁内角互补,两直线平行
两直线平行,同旁内角互补
04
课堂练习
基础题
1.关于证明,下列说法不正确的是( )
A.证明是说明命题是真命题的过程
B.要判定一个命题是真命题常常通过推理的方式
C.要说明一个命题是假命题常采用举反例的方式
D.真命题与假命题都可以通过举反例来说明
D
04
课堂练习
基础题
2. 如图,下列证明正确的是( C )
A. 因为BC∥AD,所以∠1=∠4
B. 因为∠2=∠3,所以AB∥CD
C. 因为∠C+∠ADC=180°,所以AD∥BC
D. 因为BC∥AD,所以∠ABC+∠C=180°
C
3.有一条直的宽纸带,按如图所示的方式折叠,则∠α的度数等于( )
A.50° B.60°
C.75° D.85°
C
04
课堂练习
基础题
4. 如图,小明观察两个图形后,认为图①中间的圆要比图②中间的圆小,通过测量发现他的判断是? 错误 (填“正确”或“错误”)的,由此可以得出观察? 不能 (填“能”或“不能”)作为证明的依据.
错误
不能
04
课堂练习
基础题
5. 如图,AB∥CD,∠B=∠D,EF与AD交于点E,与BC的延长线交于点F. 求证:∠DEF=∠F.
解:因为AB∥CD(已知),
所以∠DCF=∠B(两直线平行,同位角相等).
因为∠B=∠D(已知),所以∠DCF=∠D(等量代换).
所以AD∥BC(内错角相等,两直线平行).
所以∠DEF=∠F(两直线平行,内错角相等)
04
课堂练习
提升题
1. 如图,∠BCD=90°,AB∥DE,则∠α与∠β满足( B )
A. ∠α+∠β=180°
B. ∠β-∠α=90°
C. ∠β=3∠α
D. ∠α+∠β=90°
B
2. 如图,若AB∥EF,∠B=40°,则当∠E=? 140° 时,BC∥DE.
140°
04
课堂练习
拓展题
1. 如图,E,F分别为四边形ABDC的边CA的延长线上两点,连结DE,BF,DE交边AB于点G,H为边CD的延长线上一点,作∠BDH的平分线DP,交边AB的延长线于点P,∠1=∠2,∠3=∠4,∠5=∠C.
试判断DE与BF是否平行,并说明理由;
解:DE∥BF 理由:因为∠3=∠4(已知),
所以BD∥CE(内错角相等,两直线平行).
所以∠5=∠BAF(两直线平行,内错角相等).
因为∠5=∠C(已知),所以∠C=∠BAF(等量代换).
所以CD∥AB(同位角相等,两直线平行).
所以∠2=∠BGD(两直线平行,内错角相等).
因为∠1=∠2(已知),所以∠BGD=∠1(等量代换).
所以DE∥BF(内错角相等,两直线平行).
05
课堂小结
1.证明:
要判断一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立。这样的推理过程叫作证明。
2.证明的格式:
证明的基本格式:因为?? ,所以……。
注意:“因为”后面是已知条件、已证、定义、定理、基本事实
等,“所以”后面是由此推出的结果。
?
06
板书设计
1.3证明(第1课时)
1.证明:
2.证明的格式:
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
