浙教版八上1.3证明(第2课时) 同步教学课件(共25张PPT)
文档属性
| 名称 | 浙教版八上1.3证明(第2课时) 同步教学课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-18 00:00:00 | ||
图片预览




文档简介
(共25张PPT)
第1章 三角形的初步认识
1.3证明(第2课时)
(浙教版)八年级
上
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
板书设计
01
教学目标
01
进一步学习综合法证明的方法与表述,体验辅助线在证明过程中的作用,发展推理能力。
02
新知导入
1.证明的概念:
要判断一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立。这样的推理过程叫作证明。
2.证明的格式:
证明的基本格式:因为 ,所以……。
02
新知导入
3.请在横线上和括号内,分别填写下面命题的证明过程和推理依据.
已知:如图,∠1与∠2互补,∠A=∠D. 求证:AB∥CD.
证明:因为∠1+∠2=180°( 已知 ),
∠2+∠3=180°( 平角的定义 ),
所以∠1= ∠3 ( 等量代换 ).
所以 AE ∥ DF ( 同位角相等,两直线平行 ).
所以 ∠AEC = ∠D ( 两直线平行,同位角相等 ).
因为∠A=∠D( 已知 ),
所以 ∠A = ∠AEC (等量代换).
所以AB∥CD( 内错角相等,两直线平行 ).
已知
平角的定义
∠3
等量代换
AE
DF
同位角相等,两直线平行
∠AEC
∠D
两直线平行,同位角相等
已知
∠A
∠AEC
内错角相等,两直线平行
03
新知讲解
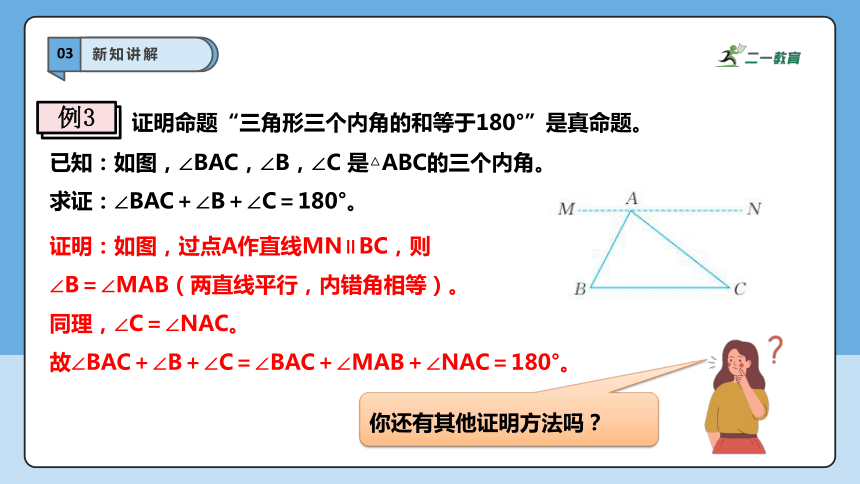
证明命题“三角形三个内角的和等于180°”是真命题。
已知:如图,∠BAC,∠B,∠C 是△ABC的三个内角。
求证:∠BAC+∠B+∠C=180°。
例3
证明:如图,过点A作直线MN∥BC,则
∠B=∠MAB(两直线平行,内错角相等)。
同理,∠C=∠NAC。
故∠BAC+∠B+∠C=∠BAC+∠MAB+∠NAC=180°。
你还有其他证明方法吗?
03
新知讲解
证明命题“三角形三个内角的和等于180°”是真命题。
已知:如图,∠BAC,∠B,∠C 是△ABC的三个内角。
求证:∠BAC+∠B+∠C=180°。
例3
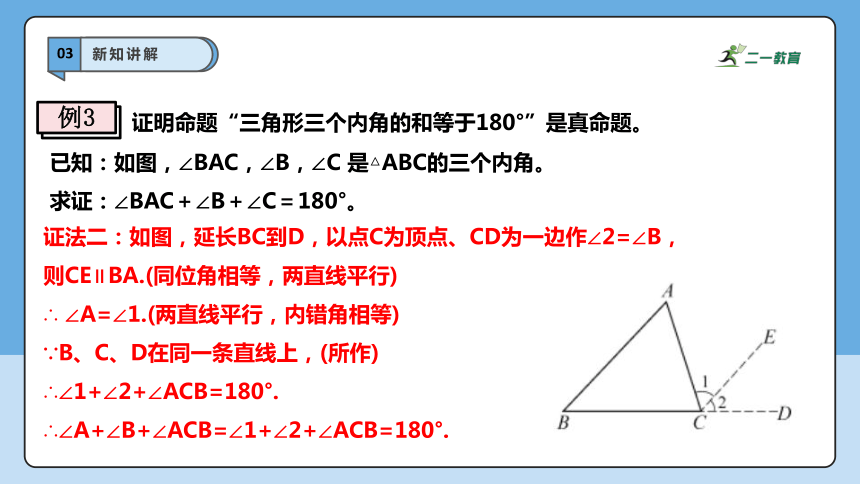
证法二:如图,延长BC到D,以点C为顶点、CD为一边作∠2=∠B,
则CE∥BA.(同位角相等,两直线平行)
∴ ∠A=∠1.(两直线平行,内错角相等)
∵B、C、D在同一条直线上,(所作)
∴∠1+∠2+∠ACB=180°.
∴∠A+∠B+∠ACB=∠1+∠2+∠ACB=180°.
03
新知探究
三角形的外角:
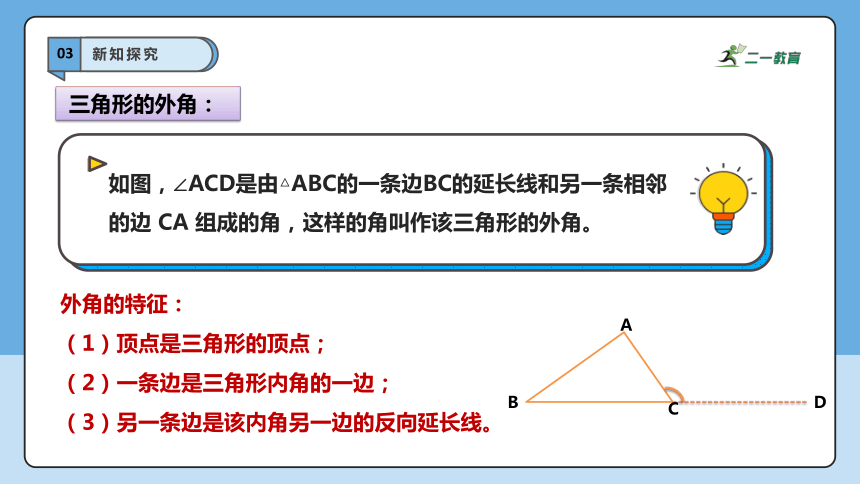
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边 CA 组成的角,这样的角叫作该三角形的外角。
A
B
C
D
外角的特征:
(1)顶点是三角形的顶点;
(2)一条边是三角形内角的一边;
(3)另一条边是该内角另一边的反向延长线。
03
新知探究
三角形的内角和定理的推论1:
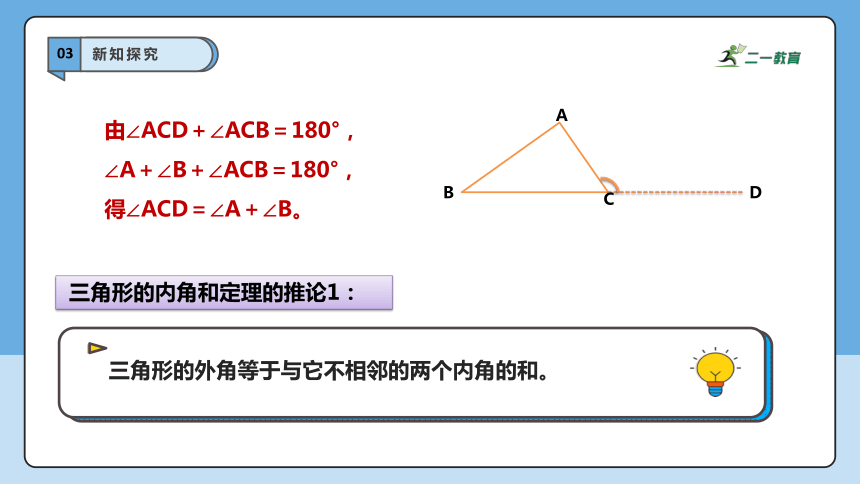
三角形的外角等于与它不相邻的两个内角的和。
由∠ACD+∠ACB=180°,
∠A+∠B+∠ACB=180°,
得∠ACD=∠A+∠B。
A
B
C
D
03
新知探究
三角形的内角和定理的推论2:
三角形的外角大于任何一个与它不相邻的内角。
A
B
C
D
∠ACD ______∠A
∠ACD ______∠B
观察:
∠ACD = ∠A +∠B
>
>
03
新知探究
三角形的外角和:
三角形的外角和等于360°。
如图,因为∠1+∠BAC=180°,∠2+∠ABC=180°,
∠3 +∠ACB=180°,
∠BAC+ ∠ABC +∠ACB=180°,
所以∠1 +∠2 +∠3 =3x180°-180°=360°。
03
新知探究
证明几何命题时,表述格式一般是:
(1)按题意画出图形。
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论。
(3)在“证明”中写出推理过程。
在解决几何问题时,有时需要添加辅助线。添辅助线的过程要写入证
明中。辅助线通常画成虚线。
03
新知讲解
已知:如图,∠B+∠D=∠BCD。求证:AB∥DE。
例4
分析:要证明 AB∥DE,根据平行线的判定方法,需要一条截线,即与
AB,DE都相交的直线。如图,延长BC,交DE于点F。只要证明∠B=
∠CFD,或∠B+∠BFE=180°,就能证明AB∥DE。
03
新知讲解
已知:如图,∠B+∠D=∠BCD。求证:AB∥DE。
例4
证明:如图,延长BC,交DE于点F。因为∠BCD是△DCF的外角,
所以∠BCD=∠D+∠CFD(三角形的外角等于与它不相邻的两个内角的和)。
又因为∠B+∠D=∠BCD(已知),
所以∠B+∠D=∠D+∠CFD,
即∠B=∠CFD。
所以AB∥DE(内错角相等,两直线平行)。
04
课堂练习
基础题
1.如图,下列关于△ABC的外角的说法正确的是( )
A.∠HBA是△ABC的外角
B.∠HBG是△ABC的外角
C.∠DCE是△ABC的外角
D.∠GBA是△ABC的外角
D
2.如图,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
A.110° B.120°
C.130° D.140°
A
04
课堂练习
基础题
3.如图,∠BDC=142°,∠B=34°,∠C=28°,则∠A= 80° .
80°
04
课堂练习
基础题
4. 已知:如图,E是AB,CD外一点,连结DE,BE,DE交AB于点F,∠D=∠B+∠E. 求证:AB∥CD.
证明:因为∠D=∠B+∠E( 已知 ),
∠BFD=∠B+∠E( 三角形的外角等于与它不相邻的两个内角的和 ),
所以∠D=∠BFD(等量代换).
所以AB∥CD( 内错角相等,两直线平行 ).
已知
三角形的外角等于与它不相邻的两个内角的和
内错角相等,两直线平行
04
课堂练习
提升题
1. 如图,在△ABC中,点E在边AC上,CD∥AB,连结DE. 若∠A=68°,∠D=54°,则∠AED的度数为( C )
A. 108° B. 112°
C. 122° D. 130°
C
2. 如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE交于点E. 若∠A=60°,则∠E的度数为 30° .
30°
04
课堂练习
拓展题
1. 如图所示为五角星和它的变形.
(1) 如图①所示为一个五角星,求∠A+∠B+∠C+∠D+∠E的度数.
解:(1) 连结CD,设CE与BD的交点为O. 在△ACD中,∠A+∠ACE+∠ECD+∠BDC+∠ADB=∠A+∠ACD+∠ADC=180°.因为∠EOD是△BOE,△COD的外角,所以∠EOD=∠B+∠E=∠ECD+∠BDC. 所以∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠ECD+∠BDC+∠ACE+∠ADB=180°
04
课堂练习
拓展题
(2) 如图②,当把图①中的点A向下移动到线段BE上时,五个角的度数和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?请说明理由.
解:(2) 无变化 理由:因为∠CAD+∠DAE+∠BAC=180°(平角的定义),∠DAE,∠BAC分别是△BAD,△CAE的外角(外角的定义),所以∠DAE=∠B+∠D,∠BAC=∠C+∠E(三角形的外角等于与它不相邻的两个内角的和).所以∠CAD+∠B+∠C+∠D+∠E=∠CAD+∠DAE+∠BAC=180°(等量代换).
05
课堂小结
1.三角形的外角:
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边 CA 组成的角,这样的角叫作该三角形的外角。
2.三角形内角和定理的推论:
三角形的外角等于与它不相邻的两个内角的和。
三角形的外角大于任何一个与它不相邻的内角。
3.三角形的外角和:
三角形的外角和等于360°。
A
B
C
D
05
课堂小结
4.证明几何命题时,表述格式一般是:
(1)按题意画出图形。
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论。
(3)在“证明”中写出推理过程。
注意:在解决几何问题时,有时需要添加辅助线。添辅助线的过程要写入证
明中。辅助线通常画成虚线。
06
板书设计
1.3证明(第2课时)
1.三角形内角和定理的证明:
2.三角形的外角及外角和:
3.三角形内角和定理的推论:
4.证明几何命题时的表述格式:
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第1章 三角形的初步认识
1.3证明(第2课时)
(浙教版)八年级
上
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
板书设计
01
教学目标
01
进一步学习综合法证明的方法与表述,体验辅助线在证明过程中的作用,发展推理能力。
02
新知导入
1.证明的概念:
要判断一个命题是真命题,往往需要从命题的条件出发,根据已知的定义、基本事实、定理(包括推论),一步一步推得结论成立。这样的推理过程叫作证明。
2.证明的格式:
证明的基本格式:因为 ,所以……。
02
新知导入
3.请在横线上和括号内,分别填写下面命题的证明过程和推理依据.
已知:如图,∠1与∠2互补,∠A=∠D. 求证:AB∥CD.
证明:因为∠1+∠2=180°( 已知 ),
∠2+∠3=180°( 平角的定义 ),
所以∠1= ∠3 ( 等量代换 ).
所以 AE ∥ DF ( 同位角相等,两直线平行 ).
所以 ∠AEC = ∠D ( 两直线平行,同位角相等 ).
因为∠A=∠D( 已知 ),
所以 ∠A = ∠AEC (等量代换).
所以AB∥CD( 内错角相等,两直线平行 ).
已知
平角的定义
∠3
等量代换
AE
DF
同位角相等,两直线平行
∠AEC
∠D
两直线平行,同位角相等
已知
∠A
∠AEC
内错角相等,两直线平行
03
新知讲解
证明命题“三角形三个内角的和等于180°”是真命题。
已知:如图,∠BAC,∠B,∠C 是△ABC的三个内角。
求证:∠BAC+∠B+∠C=180°。
例3
证明:如图,过点A作直线MN∥BC,则
∠B=∠MAB(两直线平行,内错角相等)。
同理,∠C=∠NAC。
故∠BAC+∠B+∠C=∠BAC+∠MAB+∠NAC=180°。
你还有其他证明方法吗?
03
新知讲解
证明命题“三角形三个内角的和等于180°”是真命题。
已知:如图,∠BAC,∠B,∠C 是△ABC的三个内角。
求证:∠BAC+∠B+∠C=180°。
例3
证法二:如图,延长BC到D,以点C为顶点、CD为一边作∠2=∠B,
则CE∥BA.(同位角相等,两直线平行)
∴ ∠A=∠1.(两直线平行,内错角相等)
∵B、C、D在同一条直线上,(所作)
∴∠1+∠2+∠ACB=180°.
∴∠A+∠B+∠ACB=∠1+∠2+∠ACB=180°.
03
新知探究
三角形的外角:
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边 CA 组成的角,这样的角叫作该三角形的外角。
A
B
C
D
外角的特征:
(1)顶点是三角形的顶点;
(2)一条边是三角形内角的一边;
(3)另一条边是该内角另一边的反向延长线。
03
新知探究
三角形的内角和定理的推论1:
三角形的外角等于与它不相邻的两个内角的和。
由∠ACD+∠ACB=180°,
∠A+∠B+∠ACB=180°,
得∠ACD=∠A+∠B。
A
B
C
D
03
新知探究
三角形的内角和定理的推论2:
三角形的外角大于任何一个与它不相邻的内角。
A
B
C
D
∠ACD ______∠A
∠ACD ______∠B
观察:
∠ACD = ∠A +∠B
>
>
03
新知探究
三角形的外角和:
三角形的外角和等于360°。
如图,因为∠1+∠BAC=180°,∠2+∠ABC=180°,
∠3 +∠ACB=180°,
∠BAC+ ∠ABC +∠ACB=180°,
所以∠1 +∠2 +∠3 =3x180°-180°=360°。
03
新知探究
证明几何命题时,表述格式一般是:
(1)按题意画出图形。
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论。
(3)在“证明”中写出推理过程。
在解决几何问题时,有时需要添加辅助线。添辅助线的过程要写入证
明中。辅助线通常画成虚线。
03
新知讲解
已知:如图,∠B+∠D=∠BCD。求证:AB∥DE。
例4
分析:要证明 AB∥DE,根据平行线的判定方法,需要一条截线,即与
AB,DE都相交的直线。如图,延长BC,交DE于点F。只要证明∠B=
∠CFD,或∠B+∠BFE=180°,就能证明AB∥DE。
03
新知讲解
已知:如图,∠B+∠D=∠BCD。求证:AB∥DE。
例4
证明:如图,延长BC,交DE于点F。因为∠BCD是△DCF的外角,
所以∠BCD=∠D+∠CFD(三角形的外角等于与它不相邻的两个内角的和)。
又因为∠B+∠D=∠BCD(已知),
所以∠B+∠D=∠D+∠CFD,
即∠B=∠CFD。
所以AB∥DE(内错角相等,两直线平行)。
04
课堂练习
基础题
1.如图,下列关于△ABC的外角的说法正确的是( )
A.∠HBA是△ABC的外角
B.∠HBG是△ABC的外角
C.∠DCE是△ABC的外角
D.∠GBA是△ABC的外角
D
2.如图,∠A=50°,∠C=70°,则外角∠ABD的度数是( )
A.110° B.120°
C.130° D.140°
A
04
课堂练习
基础题
3.如图,∠BDC=142°,∠B=34°,∠C=28°,则∠A= 80° .
80°
04
课堂练习
基础题
4. 已知:如图,E是AB,CD外一点,连结DE,BE,DE交AB于点F,∠D=∠B+∠E. 求证:AB∥CD.
证明:因为∠D=∠B+∠E( 已知 ),
∠BFD=∠B+∠E( 三角形的外角等于与它不相邻的两个内角的和 ),
所以∠D=∠BFD(等量代换).
所以AB∥CD( 内错角相等,两直线平行 ).
已知
三角形的外角等于与它不相邻的两个内角的和
内错角相等,两直线平行
04
课堂练习
提升题
1. 如图,在△ABC中,点E在边AC上,CD∥AB,连结DE. 若∠A=68°,∠D=54°,则∠AED的度数为( C )
A. 108° B. 112°
C. 122° D. 130°
C
2. 如图,在△ABC中,BE是∠ABC的平分线,CE是外角∠ACM的平分线,BE与CE交于点E. 若∠A=60°,则∠E的度数为 30° .
30°
04
课堂练习
拓展题
1. 如图所示为五角星和它的变形.
(1) 如图①所示为一个五角星,求∠A+∠B+∠C+∠D+∠E的度数.
解:(1) 连结CD,设CE与BD的交点为O. 在△ACD中,∠A+∠ACE+∠ECD+∠BDC+∠ADB=∠A+∠ACD+∠ADC=180°.因为∠EOD是△BOE,△COD的外角,所以∠EOD=∠B+∠E=∠ECD+∠BDC. 所以∠A+∠B+∠E+∠ACE+∠ADB=∠A+∠ECD+∠BDC+∠ACE+∠ADB=180°
04
课堂练习
拓展题
(2) 如图②,当把图①中的点A向下移动到线段BE上时,五个角的度数和(即∠CAD+∠B+∠C+∠D+∠E)有无变化?请说明理由.
解:(2) 无变化 理由:因为∠CAD+∠DAE+∠BAC=180°(平角的定义),∠DAE,∠BAC分别是△BAD,△CAE的外角(外角的定义),所以∠DAE=∠B+∠D,∠BAC=∠C+∠E(三角形的外角等于与它不相邻的两个内角的和).所以∠CAD+∠B+∠C+∠D+∠E=∠CAD+∠DAE+∠BAC=180°(等量代换).
05
课堂小结
1.三角形的外角:
如图,∠ACD是由△ABC的一条边BC的延长线和另一条相邻的边 CA 组成的角,这样的角叫作该三角形的外角。
2.三角形内角和定理的推论:
三角形的外角等于与它不相邻的两个内角的和。
三角形的外角大于任何一个与它不相邻的内角。
3.三角形的外角和:
三角形的外角和等于360°。
A
B
C
D
05
课堂小结
4.证明几何命题时,表述格式一般是:
(1)按题意画出图形。
(2)分清命题的条件和结论,结合图形,在“已知”中写出条件,在“求证”中写出结论。
(3)在“证明”中写出推理过程。
注意:在解决几何问题时,有时需要添加辅助线。添辅助线的过程要写入证
明中。辅助线通常画成虚线。
06
板书设计
1.3证明(第2课时)
1.三角形内角和定理的证明:
2.三角形的外角及外角和:
3.三角形内角和定理的推论:
4.证明几何命题时的表述格式:
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
