1.5 全等三角形的判定 专题练习(含答案)
文档属性
| 名称 | 1.5 全等三角形的判定 专题练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 61.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-30 07:51:58 | ||
图片预览

文档简介
1.5
三角形全等的判定
专题一
利用全等探究线段数量关系
1.
如图,已知∠AOB=90°,OM
( http: / / www.21cnjy.com )是∠AOB的平分线,将三角板的直角顶P在射线OM上滑动,两直角边分别与OA、OB交于C、D.PC和PD有怎样的数量关系,证明你的结论.
( http: / / www.21cnjy.com )
2.
如图,已知AB=DC,AC=BD,AC、BD相交于点E,过E点作EF∥BC,交CD于F.
⑴根据给出的条件,可以直接证明哪两个三角形全等?并加以证明.
⑵EF平分∠DEC吗?为什么?
( http: / / www.21cnjy.com )
3.
如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2-GE2=EA2.
专题二
综合探究题
4.
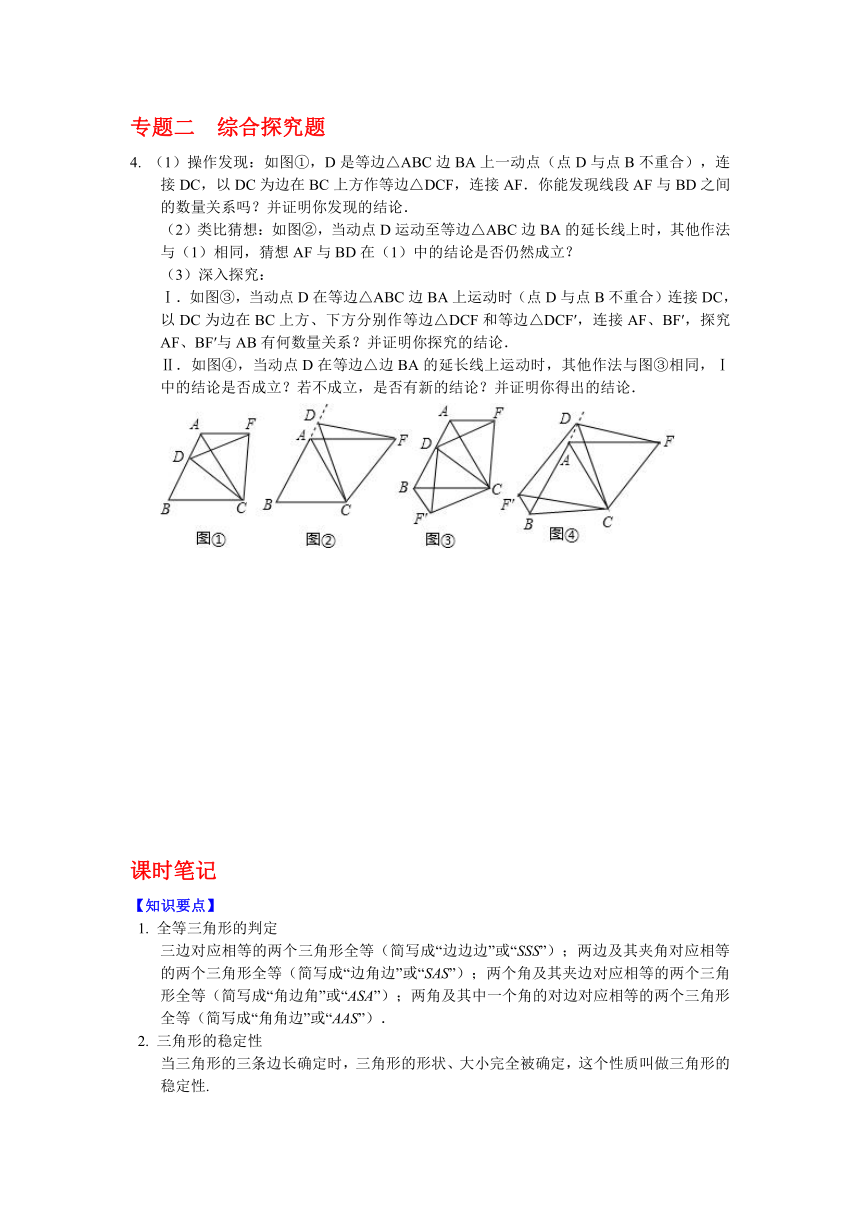
(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
课时笔记
【知识要点】
1.
全等三角形的判定
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”);两边及其夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”);两个角及其夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”);两角及其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”).
2.
三角形的稳定性
当三角形的三条边长确定时,三角形的形状、大小完全被确定,这个性质叫做三角形的稳定性.
3.
线段的垂直平分线的概念与性质
概念:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
性质:线段垂直平分线上的点到线段两端的距离相等.
4.
角平分线的性质
角平分线上的点到角两边的距离相等.
【温馨提示】
1.
线段的垂直平分线是一条直线,不是射线也不是线段.
2.
证明两个三角形全等,需写出所需的三组条件,并用大括号括在一起,注意对应位置.
3.
书写证明过程要注意格式,即:①准备条件:把题中没有直接的条件证明出来;②指明范围:在哪两个三角形中;③摆齐条件:把要证明的两个三角形全等的条件按顺序摆好;④得出结论:得出三角形全等的纵论.
【方法技巧】
1.
要说明两条线段相等的方法可以通过说明三角形全等来解决.
2.
要充分挖掘隐含条件,如公共边,当公共边是对应边时,它们是相等的.
3.
需要抓住图形特征,有时需运用等式的性质创造对应边相等的条件,从而证两个三角形全等.
参考答案:
1.
解:PC=PD.
( http: / / www.21cnjy.com )
证明:如图,作PE⊥OC于E,PF⊥OB于F.
可得∠PEC=∠PFD=90°,PE=PF.
又∵∠CPE+∠EPD=∠FPD+∠EPD=90°,
∴∠EPC
=∠FPD.
∴△CPE≌△DPF(ASA).
∴PC=PD.
解:⑴可以直接证明△ABC≌△DCB.
∵AB=DC,AC=BD,BC=CB,
∴△ABC≌△DCB.
⑵∵△ABC≌△DCB,
∴∠ACB
=∠DBC.
又∵EF∥BC,
∴∠ACB
=∠FEC,
∴∠DBC
=∠DEF,即∠FEC
=∠DEF.
∴EF平分∠DEC.
证明:(1)BH=AC.
∵CD⊥AB,BE⊥AC,
∴∠BDH=∠BEC=∠CDA=90°.
( http: / / www.21cnjy.com )∵∠ABC=45°,
∴∠BCD=180°-90°-45°=45°=∠ABC.
∴DB=DC,
∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°,
∴∠HBD=∠ACD.
在△DBH和△DCA中
∴△DBH≌△DCA(ASA),
∴BH=AC.
(2)连接CG,
∵∠ABC=45°,CD⊥AB,
∴∠BCD=90° ∠ABC=45°=∠ABC,
∴DB=CD.
∵F为BC的中点,
∴DF垂直平分BC.∴BG=CG.
∵∠ABE=∠CBE,BE⊥AC,∴EC=EA.
在Rt△CGE中,由勾股定理得:CG2-GE2=CE2.
∵CE=AE,BG=CG,
∴BG2-GE2=EA2.
解:(1)AF=BD.
证明如下:∵△AB
( http: / / www.21cnjy.com )C是等边三角形(已知),
∴BC=AC,∠BCA=60°(等边三角形的性质).
同理知,DC=CF,∠DCF=60°.
∴∠BCA-∠DCA=∠DCF-∠DCA,即∠BCD=∠ACF.
在△BCD和△ACF中,
∴△BCD≌△ACF(SAS).
∴BD=AF(全等三角形的对应边相等).
(2)证明过程同(1),证得△BCD≌△ACF(SAS),则AF=BD(全等三角形的对应边相等),所以当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,AF=BD仍然成立.
(3)Ⅰ.AF+BF′=AB.
证明如下:由(1)知,△BCD≌△ACF(SAS),则BD=AF;
同理△BCF′≌△ACD,则BF′=AD.
∴AF+BF′=BD+AD=AB;
Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′.
证明如下:在△BCF′和△ACD中,
∴△BCF′≌△ACD(SAS).
∴BF′=AD(全等三角形的对应边相等).
又由(2)知,AF=BD,
∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.
三角形全等的判定
专题一
利用全等探究线段数量关系
1.
如图,已知∠AOB=90°,OM
( http: / / www.21cnjy.com )是∠AOB的平分线,将三角板的直角顶P在射线OM上滑动,两直角边分别与OA、OB交于C、D.PC和PD有怎样的数量关系,证明你的结论.
( http: / / www.21cnjy.com )
2.
如图,已知AB=DC,AC=BD,AC、BD相交于点E,过E点作EF∥BC,交CD于F.
⑴根据给出的条件,可以直接证明哪两个三角形全等?并加以证明.
⑵EF平分∠DEC吗?为什么?
( http: / / www.21cnjy.com )
3.
如图,在△ABC中,∠ABC=45°,CD⊥AB,BE⊥AC,垂足分别为D,E,F为BC中点,BE与DF,DC分别交于点G,H,∠ABE=∠CBE.
(1)线段BH与AC相等吗?若相等给予证明,若不相等请说明理由;
(2)求证:BG2-GE2=EA2.
专题二
综合探究题
4.
(1)操作发现:如图①,D是等边△ABC边BA上一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF.你能发现线段AF与BD之间的数量关系吗?并证明你发现的结论.
(2)类比猜想:如图②,当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,猜想AF与BD在(1)中的结论是否仍然成立?
(3)深入探究:
Ⅰ.如图③,当动点D在等边△ABC边BA上运动时(点D与点B不重合)连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF、BF′,探究AF、BF′与AB有何数量关系?并证明你探究的结论.
Ⅱ.如图④,当动点D在等边△边BA的延长线上运动时,其他作法与图③相同,Ⅰ中的结论是否成立?若不成立,是否有新的结论?并证明你得出的结论.
课时笔记
【知识要点】
1.
全等三角形的判定
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”);两边及其夹角对应相等的两个三角形全等(简写成“边角边”或“SAS”);两个角及其夹边对应相等的两个三角形全等(简写成“角边角”或“ASA”);两角及其中一个角的对边对应相等的两个三角形全等(简写成“角角边”或“AAS”).
2.
三角形的稳定性
当三角形的三条边长确定时,三角形的形状、大小完全被确定,这个性质叫做三角形的稳定性.
3.
线段的垂直平分线的概念与性质
概念:垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线.
性质:线段垂直平分线上的点到线段两端的距离相等.
4.
角平分线的性质
角平分线上的点到角两边的距离相等.
【温馨提示】
1.
线段的垂直平分线是一条直线,不是射线也不是线段.
2.
证明两个三角形全等,需写出所需的三组条件,并用大括号括在一起,注意对应位置.
3.
书写证明过程要注意格式,即:①准备条件:把题中没有直接的条件证明出来;②指明范围:在哪两个三角形中;③摆齐条件:把要证明的两个三角形全等的条件按顺序摆好;④得出结论:得出三角形全等的纵论.
【方法技巧】
1.
要说明两条线段相等的方法可以通过说明三角形全等来解决.
2.
要充分挖掘隐含条件,如公共边,当公共边是对应边时,它们是相等的.
3.
需要抓住图形特征,有时需运用等式的性质创造对应边相等的条件,从而证两个三角形全等.
参考答案:
1.
解:PC=PD.
( http: / / www.21cnjy.com )
证明:如图,作PE⊥OC于E,PF⊥OB于F.
可得∠PEC=∠PFD=90°,PE=PF.
又∵∠CPE+∠EPD=∠FPD+∠EPD=90°,
∴∠EPC
=∠FPD.
∴△CPE≌△DPF(ASA).
∴PC=PD.
解:⑴可以直接证明△ABC≌△DCB.
∵AB=DC,AC=BD,BC=CB,
∴△ABC≌△DCB.
⑵∵△ABC≌△DCB,
∴∠ACB
=∠DBC.
又∵EF∥BC,
∴∠ACB
=∠FEC,
∴∠DBC
=∠DEF,即∠FEC
=∠DEF.
∴EF平分∠DEC.
证明:(1)BH=AC.
∵CD⊥AB,BE⊥AC,
∴∠BDH=∠BEC=∠CDA=90°.
( http: / / www.21cnjy.com )∵∠ABC=45°,
∴∠BCD=180°-90°-45°=45°=∠ABC.
∴DB=DC,
∵∠BDH=∠BEC=∠CDA=90°,
∴∠A+∠ACD=90°,∠A+∠HBD=90°,
∴∠HBD=∠ACD.
在△DBH和△DCA中
∴△DBH≌△DCA(ASA),
∴BH=AC.
(2)连接CG,
∵∠ABC=45°,CD⊥AB,
∴∠BCD=90° ∠ABC=45°=∠ABC,
∴DB=CD.
∵F为BC的中点,
∴DF垂直平分BC.∴BG=CG.
∵∠ABE=∠CBE,BE⊥AC,∴EC=EA.
在Rt△CGE中,由勾股定理得:CG2-GE2=CE2.
∵CE=AE,BG=CG,
∴BG2-GE2=EA2.
解:(1)AF=BD.
证明如下:∵△AB
( http: / / www.21cnjy.com )C是等边三角形(已知),
∴BC=AC,∠BCA=60°(等边三角形的性质).
同理知,DC=CF,∠DCF=60°.
∴∠BCA-∠DCA=∠DCF-∠DCA,即∠BCD=∠ACF.
在△BCD和△ACF中,
∴△BCD≌△ACF(SAS).
∴BD=AF(全等三角形的对应边相等).
(2)证明过程同(1),证得△BCD≌△ACF(SAS),则AF=BD(全等三角形的对应边相等),所以当动点D运动至等边△ABC边BA的延长线上时,其他作法与(1)相同,AF=BD仍然成立.
(3)Ⅰ.AF+BF′=AB.
证明如下:由(1)知,△BCD≌△ACF(SAS),则BD=AF;
同理△BCF′≌△ACD,则BF′=AD.
∴AF+BF′=BD+AD=AB;
Ⅱ.Ⅰ中的结论不成立.新的结论是AF=AB+BF′.
证明如下:在△BCF′和△ACD中,
∴△BCF′≌△ACD(SAS).
∴BF′=AD(全等三角形的对应边相等).
又由(2)知,AF=BD,
∴AF=BD=AB+AD=AB+BF′,即AF=AB+BF′.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
