6.3 反比例函数的应用 同步练习(含答案)
文档属性
| 名称 | 6.3 反比例函数的应用 同步练习(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 136.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-07-30 15:03:44 | ||
图片预览

文档简介
6.3
反比例函数的应用
评卷人
得分
一、选择题(每小题3分,共30分)
1.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线()上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会(
)
( http: / / www.21cnjy.com )
A.
逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
2.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(,4),则△AOC的面积为(
)
( http: / / www.21cnjy.com )
A.12
B.9
C.6
D.4
3.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度(℃)随时间(小时)变化的函数图象,其中BC段是双曲线的一部分,则当=16时,大棚内的温度约为
( http: / / www.21cnjy.com )
A.18℃
B.15.5℃
C.13.5℃
D.12℃
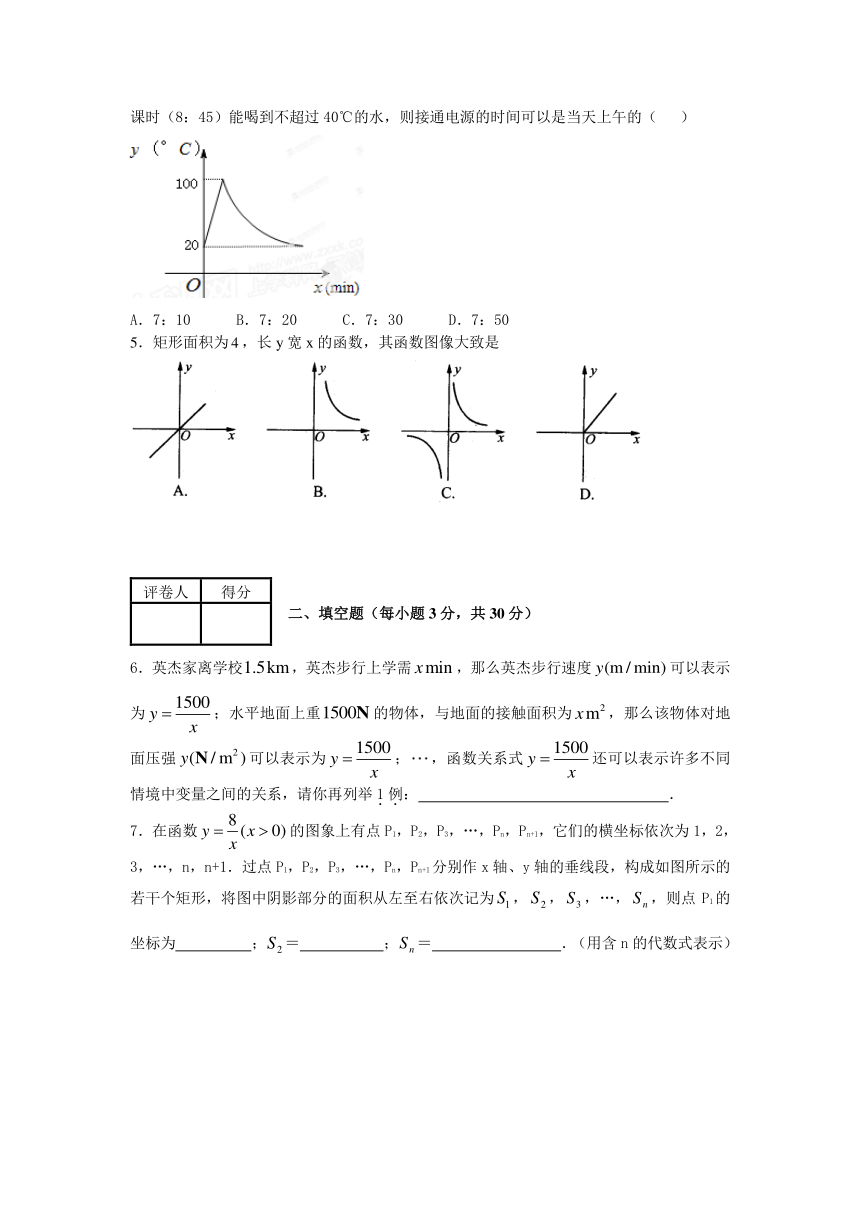
4.教室的饮水机接通电源就进入自动程序,
( http: / / www.21cnjy.com )开机加热时每分钟上升10℃,加热到100℃后停止加热。水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系。直到水温降至20℃,饮水机关机。饮水机关机后即刻自动开机。重复上述自动程序,若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,为了在上午第一节课下课时(8:45)能喝到不超过40℃的水,则接通电源的时间可以是当天上午的(
)
( http: / / www.21cnjy.com )
A.7:10
B.7:20
C.7:30
D.7:50
5.矩形面积为,长y宽x的函数,其函数图像大致是
( http: / / www.21cnjy.com )
评卷人
得分
二、填空题(每小题3分,共30分)
6.英杰家离学校,英杰步行上学需,那么英杰步行速度可以表示为;水平地面上重的物体,与地面的接触面积为,那么该物体对地面压强可以表示为;,函数关系式还可以表示许多不同情境中变量之间的关系,请你再列举1例:
.
7.在函数的图象上有点P1,P2,P3,…,Pn,Pn+1,它们的横坐标依次为1,2,3,…,n,n+1.过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成如图所示的若干个矩形,将图中阴影部分的面积从左至右依次记为,,,…,,则点P1的坐标为
;=
;=
.(用含n的代数式表示)
( http: / / www.21cnjy.com )
8.如下图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上,反比例函
数y=(k>0)的图像过顶点B,则k=
。
( http: / / www.21cnjy.com )
9.如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)都在函数(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
( http: / / www.21cnjy.com )
评卷人
得分
三、解答题(每小题10分,共40分)
10.(本小题满分10分)某商店第一次用6
( http: / / www.21cnjy.com )00元购进某种铅笔若干支,第二次又用600元购进该种铅笔,但这次每支的进价比第一次贵l元,所以购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价及购进的数量;
(2)若将这两次购进的铅笔按同一单价x(元
( http: / / www.21cnjy.com ),支)全部销售完毕,并要求获利不低于420元,求获利y(元)关于单价x(元/支)的函数关系式及定义域,并在直角坐标系内画出它的大致图象.
( http: / / www.21cnjy.com )
11.为了预防“甲流”,某
( http: / / www.21cnjy.com )校对教室采用药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量
y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例。现在测得药物8min燃毕,此时室内空气中每立方米含药量6mg,请根据题中所提供信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)药物燃烧时,y关于x的函数关系式
,
药物燃烧后,
y关于x的函数关系式
;
(2)研究表明,每立方米的含药量不超过1.6mg时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回教室?
12.(6分)(2014 云南)将油箱注满k升油后,轿车可行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
13.(本题满分分)某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
X(元)
3
4
5
6
y(个)
20
15
12
10
(1)根据表中的数据在平面直角坐标系中描出实数对(x,y)的对应点.
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为w元,试
( http: / / www.21cnjy.com )求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
( http: / / www.21cnjy.com )
参考答案
1.C.
2.
3.C
4.C
5.B.
6.y=.
7.(1,8);;
8.32.
9.(1,1);(,);.
10.(1)第一次每支铅笔的进价是4元,购进150支.(2)y=270x-1200(x≥6).
11.(1)y=x;y=;(2)30分钟.
12.(1)S=
(2)875千米
13.(1)如图,直接建立坐标系描点即可.
(2)y与x之间的函数关系式为:y=.
反比例函数的应用
评卷人
得分
一、选择题(每小题3分,共30分)
1.如图,在平面直角坐标系中,点A是x轴正半轴上的一个定点,点P是双曲线()上的一个动点,PB⊥y轴于点B,当点P的横坐标逐渐增大时,四边形OAPB的面积将会(
)
( http: / / www.21cnjy.com )
A.
逐渐增大
B.不变
C.逐渐减小
D.先增大后减小
2.如图,已知双曲线经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(,4),则△AOC的面积为(
)
( http: / / www.21cnjy.com )
A.12
B.9
C.6
D.4
3.某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度(℃)随时间(小时)变化的函数图象,其中BC段是双曲线的一部分,则当=16时,大棚内的温度约为
( http: / / www.21cnjy.com )
A.18℃
B.15.5℃
C.13.5℃
D.12℃
4.教室的饮水机接通电源就进入自动程序,
( http: / / www.21cnjy.com )开机加热时每分钟上升10℃,加热到100℃后停止加热。水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系。直到水温降至20℃,饮水机关机。饮水机关机后即刻自动开机。重复上述自动程序,若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,为了在上午第一节课下课时(8:45)能喝到不超过40℃的水,则接通电源的时间可以是当天上午的(
)
( http: / / www.21cnjy.com )
A.7:10
B.7:20
C.7:30
D.7:50
5.矩形面积为,长y宽x的函数,其函数图像大致是
( http: / / www.21cnjy.com )
评卷人
得分
二、填空题(每小题3分,共30分)
6.英杰家离学校,英杰步行上学需,那么英杰步行速度可以表示为;水平地面上重的物体,与地面的接触面积为,那么该物体对地面压强可以表示为;,函数关系式还可以表示许多不同情境中变量之间的关系,请你再列举1例:
.
7.在函数的图象上有点P1,P2,P3,…,Pn,Pn+1,它们的横坐标依次为1,2,3,…,n,n+1.过点P1,P2,P3,…,Pn,Pn+1分别作x轴、y轴的垂线段,构成如图所示的若干个矩形,将图中阴影部分的面积从左至右依次记为,,,…,,则点P1的坐标为
;=
;=
.(用含n的代数式表示)
( http: / / www.21cnjy.com )
8.如下图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上,反比例函
数y=(k>0)的图像过顶点B,则k=
。
( http: / / www.21cnjy.com )
9.如图,点P1(x1,y1),点P2(x2,y2),…,点Pn(xn,yn)都在函数(x>0)的图象上,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上(n是大于或等于2的正整数),已知点A1的坐标为(2,0),则点P1的坐标为 ;点P2的坐标为 ;点Pn的坐标为 (用含n的式子表示).
( http: / / www.21cnjy.com )
评卷人
得分
三、解答题(每小题10分,共40分)
10.(本小题满分10分)某商店第一次用6
( http: / / www.21cnjy.com )00元购进某种铅笔若干支,第二次又用600元购进该种铅笔,但这次每支的进价比第一次贵l元,所以购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价及购进的数量;
(2)若将这两次购进的铅笔按同一单价x(元
( http: / / www.21cnjy.com ),支)全部销售完毕,并要求获利不低于420元,求获利y(元)关于单价x(元/支)的函数关系式及定义域,并在直角坐标系内画出它的大致图象.
( http: / / www.21cnjy.com )
11.为了预防“甲流”,某
( http: / / www.21cnjy.com )校对教室采用药熏消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量
y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例。现在测得药物8min燃毕,此时室内空气中每立方米含药量6mg,请根据题中所提供信息,解答下列问题:
( http: / / www.21cnjy.com )
(1)药物燃烧时,y关于x的函数关系式
,
药物燃烧后,
y关于x的函数关系式
;
(2)研究表明,每立方米的含药量不超过1.6mg时,学生方可进教室,那么从消毒开始,至少需要经过多少分钟后,学生才能回教室?
12.(6分)(2014 云南)将油箱注满k升油后,轿车可行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.
(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);
(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?
13.(本题满分分)某商场出售一批进价为2元的贺卡,在市场营销中发现此商品的日销售单价x元与日销售量y之间有如下关系:
X(元)
3
4
5
6
y(个)
20
15
12
10
(1)根据表中的数据在平面直角坐标系中描出实数对(x,y)的对应点.
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为w元,试
( http: / / www.21cnjy.com )求出w与x之间的函数关系式,若物价局规定此贺卡的销售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
( http: / / www.21cnjy.com )
参考答案
1.C.
2.
3.C
4.C
5.B.
6.y=.
7.(1,8);;
8.32.
9.(1,1);(,);.
10.(1)第一次每支铅笔的进价是4元,购进150支.(2)y=270x-1200(x≥6).
11.(1)y=x;y=;(2)30分钟.
12.(1)S=
(2)875千米
13.(1)如图,直接建立坐标系描点即可.
(2)y与x之间的函数关系式为:y=.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
