1.5 三角形全等的判定 课件(共26张PPT) 浙教版(2024)八年级上册
文档属性
| 名称 | 1.5 三角形全等的判定 课件(共26张PPT) 浙教版(2024)八年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-21 17:54:04 | ||
图片预览



文档简介
(共26张PPT)
第一章 三角形的初步知识
1.5.1三角形全等的判定
教学目标
1.探索并掌握判定两个三角形全等的基本事实:三边对应相等的两个三角形全等(SSS).
2.了解三角形的稳定性及其应用.
3.会运用“SSS”判定两个三角形全等.
4.掌握角平分线的尺规作图.
钱塘江大桥由著名桥梁工程师茅以升设计,建成于1937年,是我国第一座铁路、公路两用双层桥.桥上有许多全等的三角形结构.
全等三角形的性质是什么?
全等三角形的对应边相等,对应角相等.
情境导入
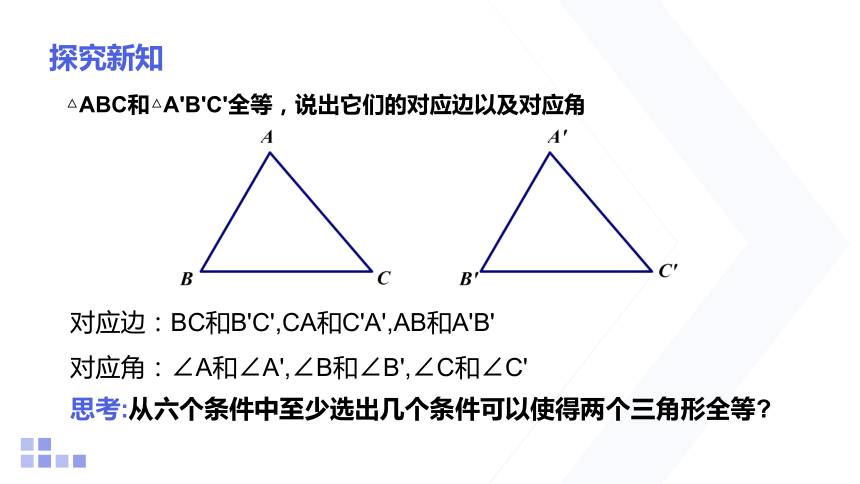
△ABC和△A'B'C'全等,说出它们的对应边以及对应角
对应边:BC和B'C',CA和C'A',AB和A'B'
对应角:∠A和∠A',∠B和∠B',∠C和∠C'
思考:从六个条件中至少选出几个条件可以使得两个三角形全等
探究新知
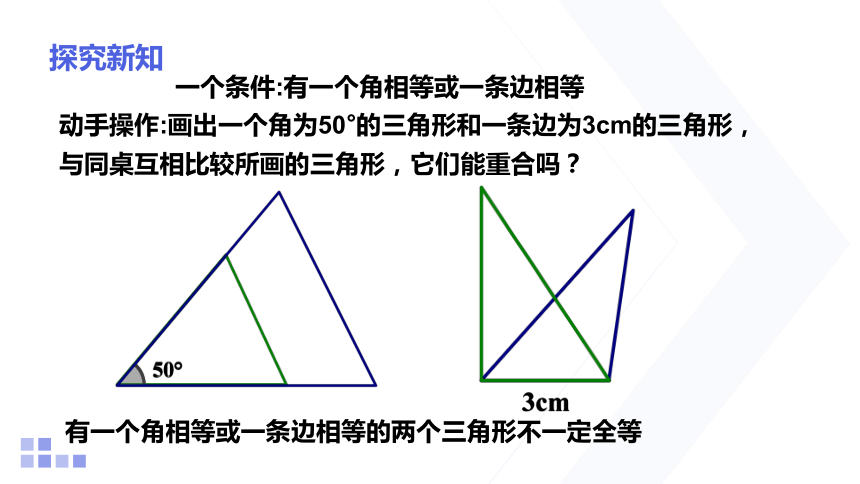
一个条件:有一个角相等或一条边相等
动手操作:画出一个角为50°的三角形和一条边为3cm的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有一个角相等或一条边相等的两个三角形不一定全等
探究新知
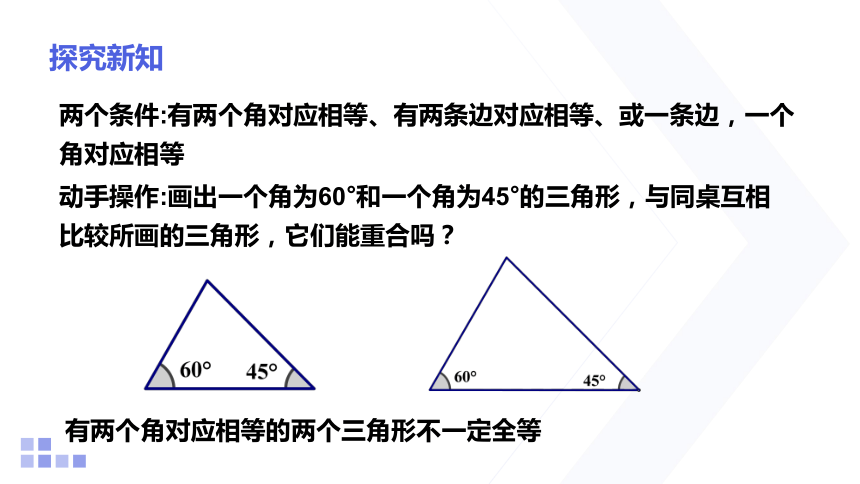
两个条件:有两个角对应相等、有两条边对应相等、或一条边,一个角对应相等
动手操作:画出一个角为60°和一个角为45°的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有两个角对应相等的两个三角形不一定全等
探究新知
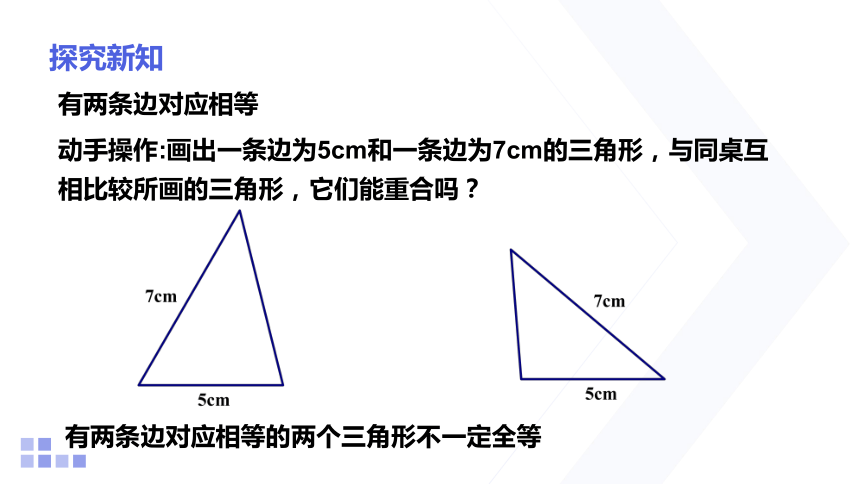
有两条边对应相等
动手操作:画出一条边为5cm和一条边为7cm的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有两条边对应相等的两个三角形不一定全等
探究新知
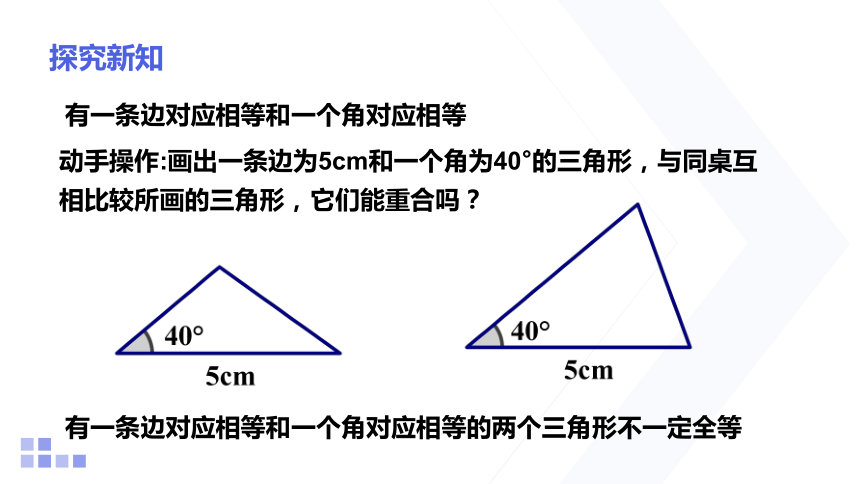
有一条边对应相等和一个角对应相等
动手操作:画出一条边为5cm和一个角为40°的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有一条边对应相等和一个角对应相等的两个三角形不一定全等
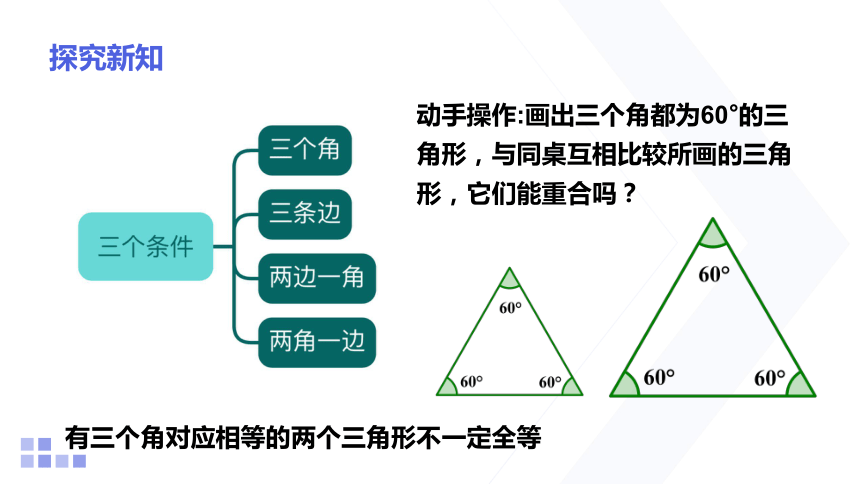
探究新知
动手操作:画出三个角都为60°的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有三个角对应相等的两个三角形不一定全等
探究新知
画法:如图
1.画线段EF=1.3cm.
2.分别以点E,F为圆心,2.5cm,1.9cm长为半径画两条圆弧,交于点D(或D').
3.连结DE,DF (或D'E,D'F). △DEF(或△D'EF)即所求作的三角形.
把你画的三角形与其他同学所画的三角形进行比较,它们能互相重合吗
按照下面的方法,用刻度尺和圆规在一张透明纸上画△DEF,使其三边长分别为1.3cm,1.9cm和2.5cm.
探究新知
一般地,我们有如下基本事实:
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
几何语言:
在△ABC和△A'BC'中
∵
∴ △ABC≌△A'BC'(SSS)
探究新知
让我们动手做下面的实验:
如图 ,把两根木条的一端用螺栓固定在一起,木条可以自由转动.在转动过程中,连结另两个端点所成的三角形的形状、大小随之改变.如果把另两个端点用螺栓固定在第三根木条上,那么构成的三角形的形状、大小就完全确定.
从上述实验可以看出,当三角形的三条边长确定时,三角形的形状、大小完全被确定,这个性质叫做三角形的稳定性,这是三角形特有的性质.
探究新知
三角形的稳定性在生产和日常生活中有广泛的应用.例如,房屋的人字架、大桥的钢梁、起重机的支架等,都采用三角形结构,以起到稳固的作用.
探究新知
例1 已知:如图,在四边形ABCD中,AB=CD,AD=CB.
求证:∠A=∠C.
证明:在 △ABD和△CDB中,
∵
∴△ABD≌△CDB (SSS).
∴∠A=∠C (全等三角形的对应角相等).
例题精讲
图1
例2 已知∠BAC(图1),用直尺和圆规作∠BAC的平分线AD,并说出该作法正确的理由.
作法:如图2.
1.以点A为圆心,适当长为半径作圆弧,与角的两边分别交于E,F两点.
2.分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于∠BAC内一点D.
3.过点A,D作射线AD.射线AD就是所求作的∠BAC的平分线.
图2
例题精讲
事实上,如图,连结DE,DF.
在 △ADF和△ADE中,
∵
∴△ADF≌△ADE (SSS)
∴∠1=∠2 (全等三角形的对应角相等),即AD平分∠BAC.
例题精讲
1.如图,木工师傅用4根木条钉成一个四边形木架ABCD,要使这个木架不变形,木工师傅至少要再钉上木条( )
4根
B. 3根
C. 2根
D. 1根
D
课堂练习
2.如图,在△ABC中,AB=AC,EB=EC,点E在AD上,依据“SSS”可以直接判定( )
A. △ADB≌△ADC
B. △ABE≌△ACE
C. △BDE≌△CDE
D. 以上都不对
B
课堂练习
3.如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=120°,则∠DHB的度数为
°.
30
课堂练习
1.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120°
B.125°
C.127°
D.104°
C
课堂练习
2.如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .
三角形的稳定性
课堂练习
如图,C是AE的中点,AB=CD,CB=ED.求证:AB∥CD.
证明:∵C是AE的中点,
∴AC=CE.
在△ABC和△CDE中,
∵
∴△ABC≌△CDE(SSS),
∴∠A=∠ECD(全等三角形的对应角相等)
∴AB∥CD.
课堂练习
“边边边”定理是什么?如何用几何语言描述?
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
几何语言:
在△ABC和△A'BC'中
∵
∴ △ABC≌△A'BC'(SSS)
课堂总结
【知识技能类作业】
1.如图,点E,F均在线段BC上,AB=D C,AE=DF,BF=CE.下列结论中,不一定成立的是( )
∠B=∠C
B. AF∥DE
C. AE=DE
D. AB∥DC
C
作业布置
【知识技能类作业】
2.如图,AB=DC,AE=DF,CE=BF,∠B=55°,则∠C=( )
A.45°
B.55°
C.35°
D.65°
B
作业布置
【知识技能类作业】
3.如图,E是BD的中点,A,E,C三点共线.若AB=AD,BC=DC,则图中全等三角形共有( )
4对
B. 3对
C. 2对
D. 1对
B
作业布置
第一章 三角形的初步知识
1.5.1三角形全等的判定
教学目标
1.探索并掌握判定两个三角形全等的基本事实:三边对应相等的两个三角形全等(SSS).
2.了解三角形的稳定性及其应用.
3.会运用“SSS”判定两个三角形全等.
4.掌握角平分线的尺规作图.
钱塘江大桥由著名桥梁工程师茅以升设计,建成于1937年,是我国第一座铁路、公路两用双层桥.桥上有许多全等的三角形结构.
全等三角形的性质是什么?
全等三角形的对应边相等,对应角相等.
情境导入
△ABC和△A'B'C'全等,说出它们的对应边以及对应角
对应边:BC和B'C',CA和C'A',AB和A'B'
对应角:∠A和∠A',∠B和∠B',∠C和∠C'
思考:从六个条件中至少选出几个条件可以使得两个三角形全等
探究新知
一个条件:有一个角相等或一条边相等
动手操作:画出一个角为50°的三角形和一条边为3cm的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有一个角相等或一条边相等的两个三角形不一定全等
探究新知
两个条件:有两个角对应相等、有两条边对应相等、或一条边,一个角对应相等
动手操作:画出一个角为60°和一个角为45°的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有两个角对应相等的两个三角形不一定全等
探究新知
有两条边对应相等
动手操作:画出一条边为5cm和一条边为7cm的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有两条边对应相等的两个三角形不一定全等
探究新知
有一条边对应相等和一个角对应相等
动手操作:画出一条边为5cm和一个角为40°的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有一条边对应相等和一个角对应相等的两个三角形不一定全等
探究新知
动手操作:画出三个角都为60°的三角形,与同桌互相比较所画的三角形,它们能重合吗?
有三个角对应相等的两个三角形不一定全等
探究新知
画法:如图
1.画线段EF=1.3cm.
2.分别以点E,F为圆心,2.5cm,1.9cm长为半径画两条圆弧,交于点D(或D').
3.连结DE,DF (或D'E,D'F). △DEF(或△D'EF)即所求作的三角形.
把你画的三角形与其他同学所画的三角形进行比较,它们能互相重合吗
按照下面的方法,用刻度尺和圆规在一张透明纸上画△DEF,使其三边长分别为1.3cm,1.9cm和2.5cm.
探究新知
一般地,我们有如下基本事实:
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
几何语言:
在△ABC和△A'BC'中
∵
∴ △ABC≌△A'BC'(SSS)
探究新知
让我们动手做下面的实验:
如图 ,把两根木条的一端用螺栓固定在一起,木条可以自由转动.在转动过程中,连结另两个端点所成的三角形的形状、大小随之改变.如果把另两个端点用螺栓固定在第三根木条上,那么构成的三角形的形状、大小就完全确定.
从上述实验可以看出,当三角形的三条边长确定时,三角形的形状、大小完全被确定,这个性质叫做三角形的稳定性,这是三角形特有的性质.
探究新知
三角形的稳定性在生产和日常生活中有广泛的应用.例如,房屋的人字架、大桥的钢梁、起重机的支架等,都采用三角形结构,以起到稳固的作用.
探究新知
例1 已知:如图,在四边形ABCD中,AB=CD,AD=CB.
求证:∠A=∠C.
证明:在 △ABD和△CDB中,
∵
∴△ABD≌△CDB (SSS).
∴∠A=∠C (全等三角形的对应角相等).
例题精讲
图1
例2 已知∠BAC(图1),用直尺和圆规作∠BAC的平分线AD,并说出该作法正确的理由.
作法:如图2.
1.以点A为圆心,适当长为半径作圆弧,与角的两边分别交于E,F两点.
2.分别以E,F为圆心,大于EF长为半径作圆弧,两条圆弧交于∠BAC内一点D.
3.过点A,D作射线AD.射线AD就是所求作的∠BAC的平分线.
图2
例题精讲
事实上,如图,连结DE,DF.
在 △ADF和△ADE中,
∵
∴△ADF≌△ADE (SSS)
∴∠1=∠2 (全等三角形的对应角相等),即AD平分∠BAC.
例题精讲
1.如图,木工师傅用4根木条钉成一个四边形木架ABCD,要使这个木架不变形,木工师傅至少要再钉上木条( )
4根
B. 3根
C. 2根
D. 1根
D
课堂练习
2.如图,在△ABC中,AB=AC,EB=EC,点E在AD上,依据“SSS”可以直接判定( )
A. △ADB≌△ADC
B. △ABE≌△ACE
C. △BDE≌△CDE
D. 以上都不对
B
课堂练习
3.如图,AB∥CD,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E、F,再分别以点E、F为圆心,大于EF长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若∠D=120°,则∠DHB的度数为
°.
30
课堂练习
1.如图,AB=AD,CB=CD,∠B=30°,∠BAD=46°,则∠ACD的度数是( )
A.120°
B.125°
C.127°
D.104°
C
课堂练习
2.如图,李叔叔家的凳子坏了,于是他给凳子加了两根木条,这样凳子就比较牢固了,他所应用的数学原理是 .
三角形的稳定性
课堂练习
如图,C是AE的中点,AB=CD,CB=ED.求证:AB∥CD.
证明:∵C是AE的中点,
∴AC=CE.
在△ABC和△CDE中,
∵
∴△ABC≌△CDE(SSS),
∴∠A=∠ECD(全等三角形的对应角相等)
∴AB∥CD.
课堂练习
“边边边”定理是什么?如何用几何语言描述?
三边对应相等的两个三角形全等(简写成“边边边”或“SSS”).
几何语言:
在△ABC和△A'BC'中
∵
∴ △ABC≌△A'BC'(SSS)
课堂总结
【知识技能类作业】
1.如图,点E,F均在线段BC上,AB=D C,AE=DF,BF=CE.下列结论中,不一定成立的是( )
∠B=∠C
B. AF∥DE
C. AE=DE
D. AB∥DC
C
作业布置
【知识技能类作业】
2.如图,AB=DC,AE=DF,CE=BF,∠B=55°,则∠C=( )
A.45°
B.55°
C.35°
D.65°
B
作业布置
【知识技能类作业】
3.如图,E是BD的中点,A,E,C三点共线.若AB=AD,BC=DC,则图中全等三角形共有( )
4对
B. 3对
C. 2对
D. 1对
B
作业布置
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
