1.5三角形全等的判定 同步练习(含部分答案)2025-2026学年浙教版数学八年级上册
文档属性
| 名称 | 1.5三角形全等的判定 同步练习(含部分答案)2025-2026学年浙教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 352.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-08-20 20:48:02 | ||
图片预览




文档简介
1.5三角形全等的判定
“边边边”
掌握基本知识
1.下列条件中,可以判定两个三角形全等的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三条边对应相等
2.下列图形中,具有稳定性的是 ( )
3.如图是“作一个角,使其等于∠AOB”的尺规作图的方法。
上述方法通过判定△C'O'D'≌△COD 得到 ,其中判定△C'O'D'≌△COD的依据是 ( )
A. SSS B. SAS
C. ASA D. AAS
4.如图,已知AC=BD,要根据“SSS”的判定方法,使得△ABC≌△DCB,需要再添加的一个条件是 。
5.如图,在△ABC 中,AD=ED,AB=EB,∠A=80°,则∠CED= °。
6.如图,已知∠AOB。
(1)利用尺规作∠DPE=∠AOB(保留作图痕迹,不要求写作法)。
(2)根据“内错角相等,两直线平行”作直线CM,使得CM∥OB。
7.如图,点 B,C,D,E在同一条直线上,AB=AE,AC=AD,BD=CE。问△ABC与△AED全等吗 试说明理由。
8.如图,已知 C 是AB 的中点,AD=CE,CD=BE。求证:
(1)△ACD≌△CBE。
(2)∠A+∠ECA=180°。
B提升关键能力
9.三月西湖,许仙与白娘子篷船借伞,还伞定情,《白蛇传》的故事流传千年。我国纸伞的制作工艺十分巧妙,如图,AB=AC,支撑杆 BD,CD 等长,当伞圈D 沿着伞柄AP 滑动时,纸伞随之打开或收拢,而无论纸伞打开还是收拢,伞柄 AP 始终平分同一平面内两条伞骨所成的∠BAC。这里推断∠BAD=∠CAD 的理由是 ( )
A.由 AB=AC,∠BAD=∠CAD,AD=AD,得△ABD≌△ACD
B.由 AB=AC,AD=AD,BD=CD,得△ABD≌△ACD
C.由 AB=AC,∠ABD=∠ACD,BD=CD,得△ABD≌△ACD
D.由 AB=AC,∠BDA=∠CDA,BD=CD,得△ABD≌△ACD
10.“经过已知角一边上的一点,作一个角等于已知角“的尺规作图过程如下:
已知:如图1,∠AOB 和OA 上一点 C。
求作:一个等于∠AOB 的角,使它的顶点为C,一边为 CA。
作法:①如图2,在 OC上取一点D,以点O为圆心,OD 长为半径画弧,交OB 于点 E;
②以点 C 为圆心,OD 长为半径画弧l,交CA于点F,以点 F 为圆心,DE 长为半径画弧,交弧l于点 G;
③作射线 CG,则∠GCA 就是所求作的角。
此作图过程的依据中不含有 ( )
A.三边对应相等的两个三角形全等
B.全等三角形的对应角相等
C.两直线平行同位角相等
D.两点确定一条直线
11.(1)如图1,点B,E,C,F在同一条直线上,AB= DE,AC= DF,BE=CF。求证:△ABC≌△DEF。
(2)如图 2,点 A,C,F,D 在同一条直线上,AF=DC,AB=DE,BC=EF。求证:△ABC≌△DEF。
(3)如图3,点 A,D 在线段 FC 上,FA=CD,AB=DE,BC=EF。求证:AB∥DE。
发展核心素养
12.[推理能力]如图,已知 AD=BC,AC=BD。求证:∠DAO=∠CBO。
第2 课时 “边角边”
A掌握基本知识
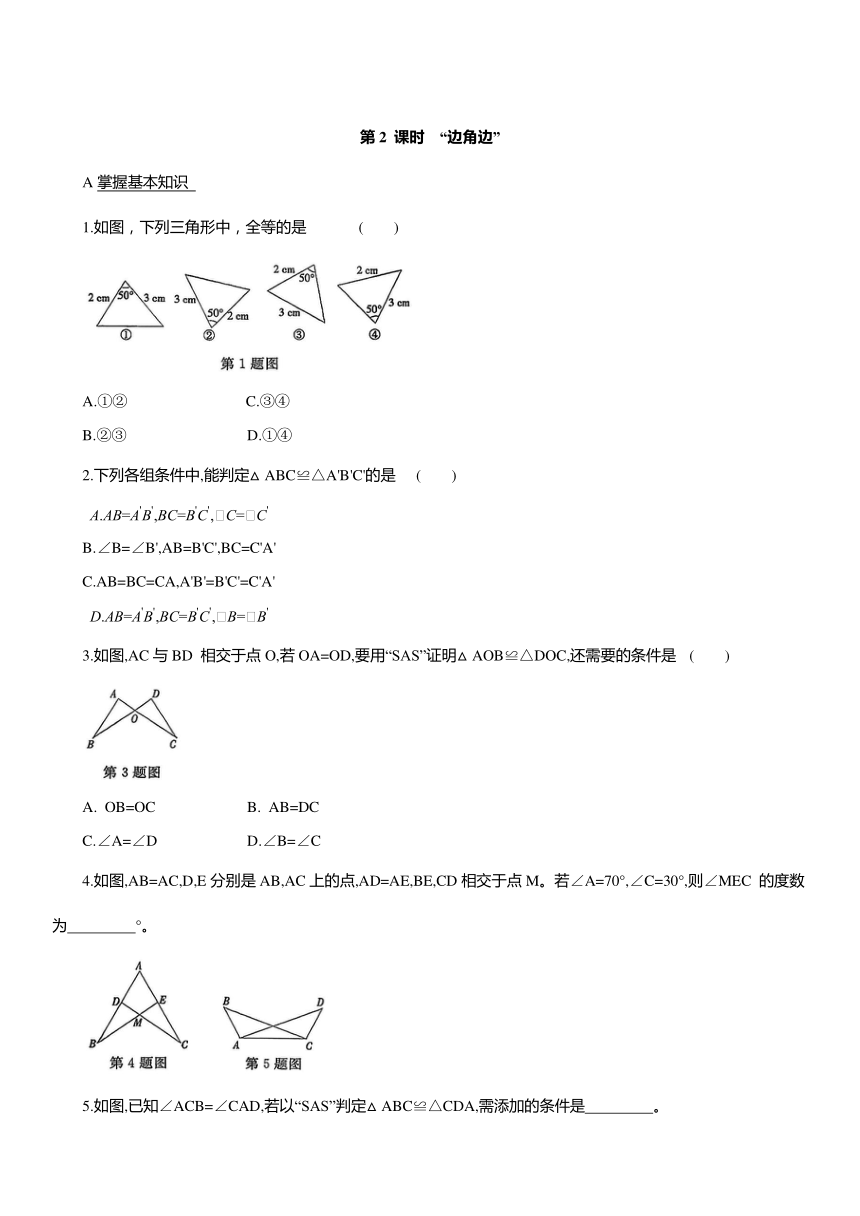
1.如图,下列三角形中,全等的是 ( )
A.①② C.③④
B.②③ D.①④
2.下列各组条件中,能判定△ABC≌△A'B'C'的是 ( )
B.∠B=∠B',AB=B'C',BC=C'A'
C.AB=BC=CA,A'B'=B'C'=C'A'
3.如图,AC与BD 相交于点O,若OA=OD,要用“SAS”证明△AOB≌△DOC,还需要的条件是 ( )
A. OB=OC B. AB=DC
C.∠A=∠D D.∠B=∠C
4.如图,AB=AC,D,E分别是AB,AC上的点,AD=AE,BE,CD相交于点M。若∠A=70°,∠C=30°,则∠MEC 的度数为 °。
5.如图,已知∠ACB=∠CAD,若以“SAS”判定△ABC≌△CDA,需添加的条件是 。
6.如图,AB是∠CAD 的平分线,AC=AD。求证:∠C=∠D。
7.如图,C是线段AB 的中点,AD=BE,∠A=∠B。求证:∠D=∠E。
8.如图,已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,夹这个角的两边长分别等于2a 和a(另作图,不得在原图上直接作图,保留作图痕迹,不写作法)。
提升关键能力
9.如图,在△ABC 中,AB=8,AC=5,AD 是△ABC的中线,则 AD 的取值范围是 ()
A.3C.2.510.如图,在△ABC 和△AED 中,AB = AE,∠BAE=∠CAD,AC=AD。求证:△ABC≌△AED。
11.如图,已知 AB=CD,点 E,F在线段 BD 上,且AF=CE。
请从①BF=DE;②∠BAF=∠DCE;③AF=CF 中,选择一个合适的作为已知条件,使得△ABF≌△CDE。你选择的条件是: (只填写一个序号)。添加条件后,请证明:AE∥CF。
12.如图,在△ABC 和△AED 中,AB=AC,AE=AD,∠BAC=∠EAD,且点 E,A,B 在同一条直线上,点C,D在直线 EB 同侧,连结BD,CE,两者相交于点 M。
(1)求证:△ABD≌△ACE。
(2)若∠CAD=100°,求∠DME 的度数。
发展核心素养
13.[推理能力]在△ABC中,AB=AC,D 是线段BC 上的一动点(不与点 B,C重合),以线段AD为边在其右侧作△ADE,使 AE=AD,∠DAE=∠BAC,连结CE。
(1) 如 图 1, 当 ∠BAC = 90°时, ∠DCE= °。
(2)如图 2,设∠BAC=α,∠DCE=β,请你探究α与β之间的数量关系,并证明你的结论。
“角边角”与“角角边”
A 掌握基本知识
1.在△ABC和△A'B'C'中,由∠A=∠A',∠B=∠B',BC=B'C', 得出△ABC≌△A'B'C'的根据是 ( )
A. SAS B. SSS C. ASA D. AAS
2.如图,已知△ABC的六个元素,则甲、乙、丙三个三角形中,与△ABC全等的是 ( )
A.甲和乙 B.乙和丙
C.只有乙 D.只有丙
3.如图,点 B,F,C,E在同一条直线上,AC=DF,∠1=∠2。如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是 ( )
A. AB=DE B.∠A=∠D
C. BF=CE D.∠B=∠D
4.下列条件中,不能判定△ABC≌△DEF的是( )
A.∠A=∠F,BA=EF,AC=FD
B.∠B=∠E,BC=EF,∠A=∠D
C.∠C=∠F=90°,∠A=60°,∠E=30°,AC=DF
D.∠A=∠D,AB=DE,∠B=∠E
5.如图,图中的字母表示三角形的边长。若要使两个三角形全等,则∠1 的度数为 ( )
A.40° B.50° C.60° D.70°
6.如图,已知AC与BF 相交于点E,AB∥CF,E为BF 的中点,若CF=7,AD=5,则 BD 的长为 。
7. 如图,若 AD 是△ABC 的高线,∠DBE =∠DAC,BD = AD, ∠AEB = 120°, 则 ∠C= °。
8.如图,∠1=∠2,∠3=∠4,BD=AC。若 AE=4,BC=11,则 ED= 。
9.如图,在△ABC 和△ADE 中,AB=AD,∠B=∠D,∠1=∠2。求证:BC=DE。
10.如图,∠C=∠D=90°,∠CBA=∠DAB。
(1)求证:△ABC≌△BAD。
(2)若∠DAB=70°,则∠CAB= °。
提升关键能力
11.如图,在△ABC中,D 为边 BC 上的一点,∠1=∠2=∠3,AC=AE。若 DE=8,BD=3,则 DC= 。
12.如图,AB=AC,∠B=∠C,则图中全等的三角形有 。
13.如图,已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于2∠α,且这两内角的夹边等于 a(可在原图上直接作图,保留痕迹,不写作法)。
14.如图,△ABC 的两条高线AD,CE 相交于点F,AF=BC。
(1)求证:△AEF≌△CEB。
(2)若 BE=4,CF=5,求 AE 的长度。
15.如图,点 B,E,C,F在同一条直线上,AC与DE 相交于点O,AC∥DF,AB∥DE,AB=DE。若 BE=1,EC=3,求 BF 的长。
发展核心素养
16.[推理能力]在△ABC 中,D,F 分别为线段AC,AB 上的点,连结 BD,CF,两者相交于点 E。
(1)如图 1,若 BD⊥AC,CF⊥AB。求证:∠BAC+∠BEC=180°。
(2)如图 2,若 BD 平分∠ABC,CF 平分∠ACB,∠BAC=60°。求证:EF=ED。
1.5三角形全等的判定
第1课时 “边边边”
1. D 2. A 3. A 4. AB=DC5.100 6.略7.△ABC≌△AED。理由略 8.略 9. B 10. C11.略 12.略
第2课时 “边角边”
1. A 2. D 3. A 4.100 5. BC=DA 6.略 7.略
8.略 9. B 10.略 11.①(或②)。证明略
12.(1)略 (2)40° 13.(1)90 (2)α+β=180°。证明略
第3课时 “角边角”与“角角边”
1. D 2. B 3. B 4. A 5. C 6.2 7.60 8.7 9.略10.(1)略 (2)20 11.5 12.△ABD≌△ACE,△BEF≌△CDF13.略 14.(1)略 (2)9 15.5 16.略
“边边边”
掌握基本知识
1.下列条件中,可以判定两个三角形全等的是( )
A.一条边对应相等 B.两条边对应相等
C.三个角对应相等 D.三条边对应相等
2.下列图形中,具有稳定性的是 ( )
3.如图是“作一个角,使其等于∠AOB”的尺规作图的方法。
上述方法通过判定△C'O'D'≌△COD 得到 ,其中判定△C'O'D'≌△COD的依据是 ( )
A. SSS B. SAS
C. ASA D. AAS
4.如图,已知AC=BD,要根据“SSS”的判定方法,使得△ABC≌△DCB,需要再添加的一个条件是 。
5.如图,在△ABC 中,AD=ED,AB=EB,∠A=80°,则∠CED= °。
6.如图,已知∠AOB。
(1)利用尺规作∠DPE=∠AOB(保留作图痕迹,不要求写作法)。
(2)根据“内错角相等,两直线平行”作直线CM,使得CM∥OB。
7.如图,点 B,C,D,E在同一条直线上,AB=AE,AC=AD,BD=CE。问△ABC与△AED全等吗 试说明理由。
8.如图,已知 C 是AB 的中点,AD=CE,CD=BE。求证:
(1)△ACD≌△CBE。
(2)∠A+∠ECA=180°。
B提升关键能力
9.三月西湖,许仙与白娘子篷船借伞,还伞定情,《白蛇传》的故事流传千年。我国纸伞的制作工艺十分巧妙,如图,AB=AC,支撑杆 BD,CD 等长,当伞圈D 沿着伞柄AP 滑动时,纸伞随之打开或收拢,而无论纸伞打开还是收拢,伞柄 AP 始终平分同一平面内两条伞骨所成的∠BAC。这里推断∠BAD=∠CAD 的理由是 ( )
A.由 AB=AC,∠BAD=∠CAD,AD=AD,得△ABD≌△ACD
B.由 AB=AC,AD=AD,BD=CD,得△ABD≌△ACD
C.由 AB=AC,∠ABD=∠ACD,BD=CD,得△ABD≌△ACD
D.由 AB=AC,∠BDA=∠CDA,BD=CD,得△ABD≌△ACD
10.“经过已知角一边上的一点,作一个角等于已知角“的尺规作图过程如下:
已知:如图1,∠AOB 和OA 上一点 C。
求作:一个等于∠AOB 的角,使它的顶点为C,一边为 CA。
作法:①如图2,在 OC上取一点D,以点O为圆心,OD 长为半径画弧,交OB 于点 E;
②以点 C 为圆心,OD 长为半径画弧l,交CA于点F,以点 F 为圆心,DE 长为半径画弧,交弧l于点 G;
③作射线 CG,则∠GCA 就是所求作的角。
此作图过程的依据中不含有 ( )
A.三边对应相等的两个三角形全等
B.全等三角形的对应角相等
C.两直线平行同位角相等
D.两点确定一条直线
11.(1)如图1,点B,E,C,F在同一条直线上,AB= DE,AC= DF,BE=CF。求证:△ABC≌△DEF。
(2)如图 2,点 A,C,F,D 在同一条直线上,AF=DC,AB=DE,BC=EF。求证:△ABC≌△DEF。
(3)如图3,点 A,D 在线段 FC 上,FA=CD,AB=DE,BC=EF。求证:AB∥DE。
发展核心素养
12.[推理能力]如图,已知 AD=BC,AC=BD。求证:∠DAO=∠CBO。
第2 课时 “边角边”
A掌握基本知识
1.如图,下列三角形中,全等的是 ( )
A.①② C.③④
B.②③ D.①④
2.下列各组条件中,能判定△ABC≌△A'B'C'的是 ( )
B.∠B=∠B',AB=B'C',BC=C'A'
C.AB=BC=CA,A'B'=B'C'=C'A'
3.如图,AC与BD 相交于点O,若OA=OD,要用“SAS”证明△AOB≌△DOC,还需要的条件是 ( )
A. OB=OC B. AB=DC
C.∠A=∠D D.∠B=∠C
4.如图,AB=AC,D,E分别是AB,AC上的点,AD=AE,BE,CD相交于点M。若∠A=70°,∠C=30°,则∠MEC 的度数为 °。
5.如图,已知∠ACB=∠CAD,若以“SAS”判定△ABC≌△CDA,需添加的条件是 。
6.如图,AB是∠CAD 的平分线,AC=AD。求证:∠C=∠D。
7.如图,C是线段AB 的中点,AD=BE,∠A=∠B。求证:∠D=∠E。
8.如图,已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,夹这个角的两边长分别等于2a 和a(另作图,不得在原图上直接作图,保留作图痕迹,不写作法)。
提升关键能力
9.如图,在△ABC 中,AB=8,AC=5,AD 是△ABC的中线,则 AD 的取值范围是 ()
A.3
11.如图,已知 AB=CD,点 E,F在线段 BD 上,且AF=CE。
请从①BF=DE;②∠BAF=∠DCE;③AF=CF 中,选择一个合适的作为已知条件,使得△ABF≌△CDE。你选择的条件是: (只填写一个序号)。添加条件后,请证明:AE∥CF。
12.如图,在△ABC 和△AED 中,AB=AC,AE=AD,∠BAC=∠EAD,且点 E,A,B 在同一条直线上,点C,D在直线 EB 同侧,连结BD,CE,两者相交于点 M。
(1)求证:△ABD≌△ACE。
(2)若∠CAD=100°,求∠DME 的度数。
发展核心素养
13.[推理能力]在△ABC中,AB=AC,D 是线段BC 上的一动点(不与点 B,C重合),以线段AD为边在其右侧作△ADE,使 AE=AD,∠DAE=∠BAC,连结CE。
(1) 如 图 1, 当 ∠BAC = 90°时, ∠DCE= °。
(2)如图 2,设∠BAC=α,∠DCE=β,请你探究α与β之间的数量关系,并证明你的结论。
“角边角”与“角角边”
A 掌握基本知识
1.在△ABC和△A'B'C'中,由∠A=∠A',∠B=∠B',BC=B'C', 得出△ABC≌△A'B'C'的根据是 ( )
A. SAS B. SSS C. ASA D. AAS
2.如图,已知△ABC的六个元素,则甲、乙、丙三个三角形中,与△ABC全等的是 ( )
A.甲和乙 B.乙和丙
C.只有乙 D.只有丙
3.如图,点 B,F,C,E在同一条直线上,AC=DF,∠1=∠2。如果根据“ASA”判定△ABC≌△DEF,那么需要补充的条件是 ( )
A. AB=DE B.∠A=∠D
C. BF=CE D.∠B=∠D
4.下列条件中,不能判定△ABC≌△DEF的是( )
A.∠A=∠F,BA=EF,AC=FD
B.∠B=∠E,BC=EF,∠A=∠D
C.∠C=∠F=90°,∠A=60°,∠E=30°,AC=DF
D.∠A=∠D,AB=DE,∠B=∠E
5.如图,图中的字母表示三角形的边长。若要使两个三角形全等,则∠1 的度数为 ( )
A.40° B.50° C.60° D.70°
6.如图,已知AC与BF 相交于点E,AB∥CF,E为BF 的中点,若CF=7,AD=5,则 BD 的长为 。
7. 如图,若 AD 是△ABC 的高线,∠DBE =∠DAC,BD = AD, ∠AEB = 120°, 则 ∠C= °。
8.如图,∠1=∠2,∠3=∠4,BD=AC。若 AE=4,BC=11,则 ED= 。
9.如图,在△ABC 和△ADE 中,AB=AD,∠B=∠D,∠1=∠2。求证:BC=DE。
10.如图,∠C=∠D=90°,∠CBA=∠DAB。
(1)求证:△ABC≌△BAD。
(2)若∠DAB=70°,则∠CAB= °。
提升关键能力
11.如图,在△ABC中,D 为边 BC 上的一点,∠1=∠2=∠3,AC=AE。若 DE=8,BD=3,则 DC= 。
12.如图,AB=AC,∠B=∠C,则图中全等的三角形有 。
13.如图,已知∠α和线段a,用尺规作一个三角形,使其一个内角等于∠α,另一个内角等于2∠α,且这两内角的夹边等于 a(可在原图上直接作图,保留痕迹,不写作法)。
14.如图,△ABC 的两条高线AD,CE 相交于点F,AF=BC。
(1)求证:△AEF≌△CEB。
(2)若 BE=4,CF=5,求 AE 的长度。
15.如图,点 B,E,C,F在同一条直线上,AC与DE 相交于点O,AC∥DF,AB∥DE,AB=DE。若 BE=1,EC=3,求 BF 的长。
发展核心素养
16.[推理能力]在△ABC 中,D,F 分别为线段AC,AB 上的点,连结 BD,CF,两者相交于点 E。
(1)如图 1,若 BD⊥AC,CF⊥AB。求证:∠BAC+∠BEC=180°。
(2)如图 2,若 BD 平分∠ABC,CF 平分∠ACB,∠BAC=60°。求证:EF=ED。
1.5三角形全等的判定
第1课时 “边边边”
1. D 2. A 3. A 4. AB=DC5.100 6.略7.△ABC≌△AED。理由略 8.略 9. B 10. C11.略 12.略
第2课时 “边角边”
1. A 2. D 3. A 4.100 5. BC=DA 6.略 7.略
8.略 9. B 10.略 11.①(或②)。证明略
12.(1)略 (2)40° 13.(1)90 (2)α+β=180°。证明略
第3课时 “角边角”与“角角边”
1. D 2. B 3. B 4. A 5. C 6.2 7.60 8.7 9.略10.(1)略 (2)20 11.5 12.△ABD≌△ACE,△BEF≌△CDF13.略 14.(1)略 (2)9 15.5 16.略
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
